2020年秋浙教版九年级数学上册第3章圆的基本性质单元培优 测试卷(Word版 含解析)
文档属性
| 名称 | 2020年秋浙教版九年级数学上册第3章圆的基本性质单元培优 测试卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 341.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 00:00:00 | ||
图片预览

文档简介
2020年秋浙教版九年级数学上册第3章圆的基本性质单元培优
测试卷解析版
一、选择题(共10题;共30分)
1.已知⊙O的半径为3,A为线段PO的中点,则当OP=5时,点A与⊙O的位置关系为( )
A.?点在圆内??B.?点在圆上????C.?点在圆外????D.?不能确定
2.在绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是(??
)
A.?????B.???????C.???????D.?
3.往直径为
的圆柱形容器内装入一些水以后,截面如图所示,若水面宽
,则水的最大深度为(???
)
A.??????B.?????C.?????D.?
4.如图,
是⊙O的直径,点C、D在⊙O上,
,则
的大小为(???
)
A.????B.?????C.?????D.?
5.如图,点A,B,C,D在⊙O上,
,点B是
的中点,则
的度数是(???
)
A.??????B.??????C.????D.?
6.如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE。若∠D=80°,则∠EAC的度数是(???
)
A.?20°????B.?25°????C.?30°????D.?35°
7.如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近(?
)
A.????????B.???????C.?????????D.?
8.如图,放置在直线l上的扇形OAB.由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的最短路径的长是(????
)
A.?2π+2????B.?3π???C.???????D.?
+2
9.如图,在扇形
中,已知
,
,过
的中点C作
,
,垂足分别为D、E,则图中阴影部分的面积为(??
)
A.???????B.??????C.??????D.?
10.如图,在平面直角坐标系中,Q是直线y=﹣
x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点
,连接
,则
的最小值为(???
)
A.?????B.???????C.?????????D.?
二、填空题(共6题;共24分)
11.在⊙O中,若弦
垂直平分半径
,则弦
所对的圆周角等于________°.
12.如图,AB为
的直径,弦
于点H
,
若
,
,则OH的长度为
________.
13.小明在手工制作课上,用面积为
,半径为
的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为________
.
14.如图,已知锐角三角形
内接于半径为2的
,
于点
,
,则
________.
15.如图,正方形
的边长为1,将其绕顶点C按逆时针方向旋转一定角度到
位置,使得点B落在对角线
上,则阴影部分的面积是________.
16.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为
,则半圆的半径OA的长为________.
三、解答题(共8题;共66分)
17.如图,在
中,
,将
绕点A逆时针旋转
,得到
,使得点B、C、D恰好在同一条直线上,求
的度数.
18.如图,△ABC的三个顶点都在⊙O上,直径AD=6cm
,
∠DAC=2∠B
,
求AC的长.
19.如图,△ABC中,AB=AC
,
⊙O是△ABC的外接圆,BO的延长交边AC于点D
.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小;
(3)当AD=2,CD=3时,求边BC的长.
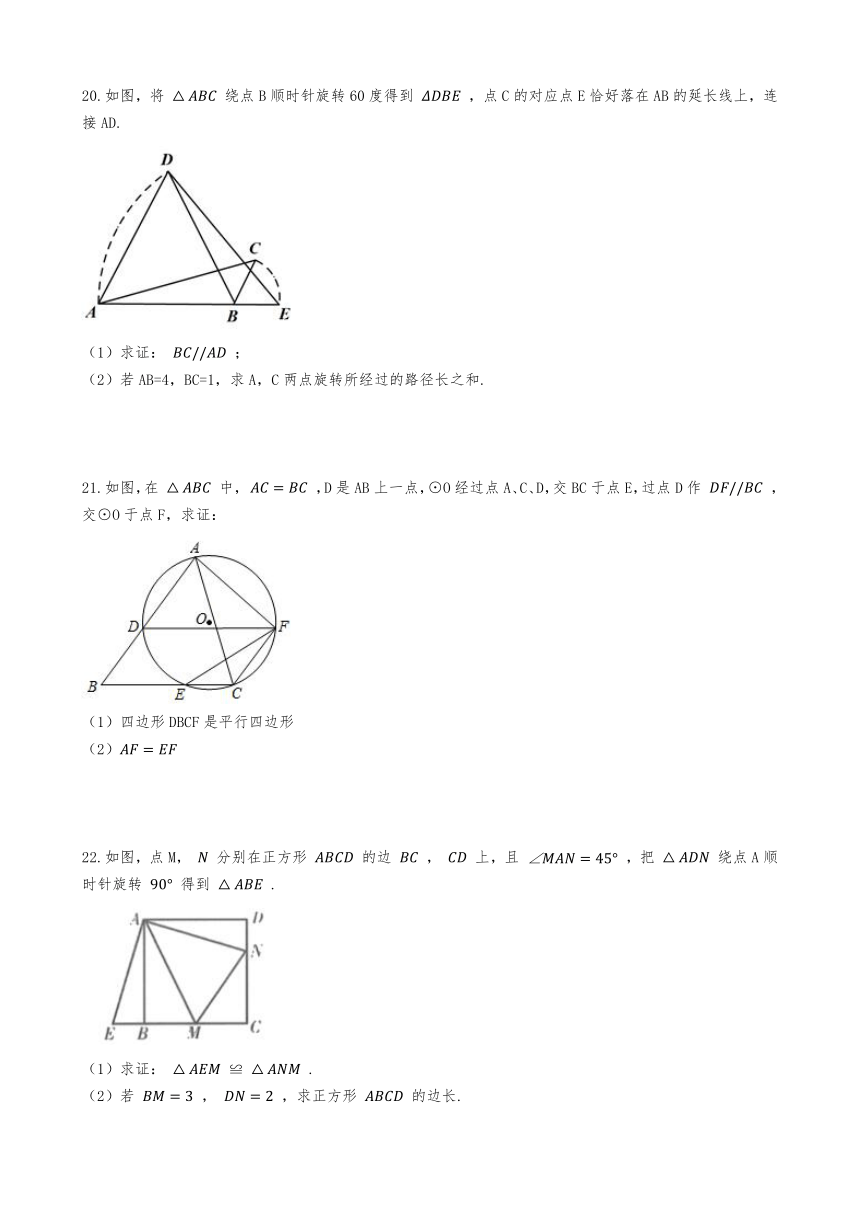
20.如图,将
绕点B顺时针旋转60度得到
,点C的对应点E恰好落在AB的延长线上,连接AD.
(1)求证:
;
(2)若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.
21.如图,在
中,
,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作
,交⊙O于点F,求证:
(1)四边形DBCF是平行四边形
(2)
22.如图,点M,
分别在正方形
的边
,
上,且
,把
绕点A顺时针旋转
得到
.
(1)求证:
≌
.
(2)若
,
,求正方形
的边长.
23.如图所示,已知A
,
B两点的坐标分别为(2
,0),(0,10),P是△AOB外接圆⊙C上的一点,OP交AB于点
D
.
(1)当OP⊥AB时,求OP;
(2)当∠AOP=30°时,求AP
.
24.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;
(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.
答案
一、选择题
1.解:∵OA=
OP=2.5,⊙O的半径为3,
∴OA<⊙O半径,
∴点A与⊙O的位置关系为:点在圆内.故答案为:A.
2.解:ACD、
不是由某个基本图形经过旋转得到的,故ACD不符合题意;
B、是由一个基本图形经过旋转得到的,故B符合题意.
故答案为:B.
3.解:过点O作OD⊥AB于D,交⊙O于E,连接OA,
由垂径定理得:
,
∵⊙O的直径为
,
∴
,
在
中,由勾股定理得:
,
∴
,
∴油的最大深度为
,
故答案为:
.
4.解:∵∠BDC=20°
∴∠BOC=2×20°=40°
∴∠AOC=180°-40°=140°
故答案为:B.
5.连接OB,
∵点B是弧AC的中点,
∴∠AOB=
∠AOC=60°,
由圆周角定理得,∠D=
∠AOB=30°,
故答案为:A.
6.∵四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°-∠D)=50°,
∵四边形AECD是圆内接四边形,∠D=80°,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB-∠ACB=30°.
故答案为:C.
7.连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC=
AB=
a,
则正方形桌面与翻折成的圆形桌面的面积之比为:
,
故答案为:C.
8.解:如图,
?
点O的运动路径的长=
的长+O1O2+
的长=
+
+
=
,
故答案为:C.
9.连接OC
点C为弧AB的中点
在
和
中
又
四边形CDOE为正方形
由扇形面积公式得
故答案为:B.
10.解:作QM⊥x轴于点M,Q′N⊥x轴于N,
设Q(
,
),则PM=
,QM=
,
∵∠PMQ=∠PNQ′=∠QPQ′=90°,
∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,
∴∠QPM=∠PQ′N,
在△PQM和△Q′PN中,
,
∴△PQM≌△Q′PN(AAS),
∴PN=QM=
,Q′N=PM=
,
∴ON=1+PN=
,
∴Q′(
,
),
∴OQ′2=(
)2+(
)2=
m2﹣5m+10=
(m﹣2)2+5,
当m=2时,OQ′2有最小值为5,
∴OQ′的最小值为
,
故答案为:B.
二、填空题
11.设弦
垂直平分半径
于点E,连接OB、OC、AB、AC,且在优弧BC上取点F,连接BF、CF,
∴OB=AB,OC=AC,
∵OB=OC,
∴四边形OBAC是菱形,
∴∠BOC=2∠BOE,
∵OB=OA,OE=
,
∴cos∠BOE=
,
∴∠BOE=60°,
∴∠BOC=∠BAC=120°,
∴∠BFC=
∠BOC=60°,
∴
弦
所对的圆周角为120°或60°,
故答案为:120或60.
12.连接OC,
Rt△OCH中,OC=
AB=5,CH=
CD=4;
由勾股定理,得:OH=
;
即线段OH的长为3.
故答案为:3.
13.由
得:扇形的弧长=
(厘米),
圆锥的底面半径=
(厘米).
故答案是:10.
14.解:连接OB和OC,
∵△ABC内接于半径为2的圆O,∠BAC=60°,
∴∠BOC=120°,OB=OC=2,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,
∴∠OBD=30°,
∴OD=
OB=1,
故答案为:1.
15.解:过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=
EC=
,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴△PEC≌△PBC(HL),
∴PB=PE,
又∠PFB=45°,∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x
,
则EP=BP=
,
∵MP+BP=MB,
∴
,解得
,
∴BP=
,
∴阴影部分的面积=
.
故答案为:
.
16.解:如图,连接
?点C、D分别是半圆AOB上的三等分点,
?
?
为等边三角形,
?
?
?
?
?
解得:
(负根舍去),
故答案为:3
三、解答题
17.
解:∵将
绕点A逆时针旋转150°,得到
,
.
∵点B、C、D恰好在同一条直线上
是顶角为150°的等腰三角形,
,
,
.
18.
解:如图,连接OC
,
∵∠AOC=2∠B
,
∠DAC=2∠B
,
∴∠AOC=∠DAC
,
∴AO=AC
,
又∵OA=OC
,
∴△AOC是等边三角形,
∴AC=AO=
AD=3cm
.
19.
(1)连接OA,如下图1所示:
∵AB=AC,
∴
=
,
∴OA⊥BC,
∴∠BAO=∠CAO.
∵OA=OB,
∴∠ABD=∠BAO,
∴∠BAC=2∠ABD.
(2)如图2中,延长AO交BC于H.
①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD.
∵AB=AC,
∴∠ABC=∠C,
∴∠DBC=2∠ABD.
∵∠DBC+∠C+∠BDC=180°,
∴8∠ABD=180°,
∴∠C=3∠ABD=67.5°.
②若CD=CB,则∠CBD=∠CDB=3∠ABD,∴∠C=4∠ABD.
∵∠DBC+∠C+∠CDB=180°,
∴10∠ABD=180°,
∴∠BCD=4∠ABD=72°.
③若DB=DC,则D与A重合,这种情形不存在.
综上所述:∠C的值为67.5°或72°.
(3)如图3中,过A点作AE
BC交BD的延长线于E.
则
=
=
,且BC=2BH,
∴
=
=
,
设OB=OA=4a,OH=3a.
则在Rt△ABH和Rt△OBH中,
∵BH2=AB2﹣AH2=OB2﹣OH2
,
∴25
-
49a2=16a2﹣9a2
,
∴a2=
,
∴BH=
,
∴BC=2BH=
.
故答案为:
.
20.
(1)证明:由旋转性质得:
是等边三角形
所以
∴
;
(2)解:依题意得:AB=BD=4,BC=BE=1,
所以A,C两点经过的路径长之和为
.
21.
(1)证明:
,
,
,
,
又
,
?
?
四边形
是平行四边形.
(2)证明:如图,连接
,
四边形
是
的内接四边形
22.
(1)证明:由旋转的性质得:
四边形ABCD是正方形
,即
,即
在
和
中,
;
(2)解:设正方形
的边长为x,则
由旋转的性质得:
由(1)已证:
又
四边形ABCD是正方形
则在
中,
,即
解得
或
(不符题意,舍去)
故正方形
的边长为6.
23.
(1)解:∵A,B两点的坐标分别为(2
,0),(0,10),
∴AO=2
,OB=10,
∵AO⊥BO,
∴AB=
=4
,
∵OP⊥AB,
∴
=
,CD=DP,
∴CD=
,
∴OP=2CD=
;
(2)解:连接CP,如图所示:
∵∠AOP=30°,
∴∠ACP=60°,
∵CP=CA,
∴△ACP为等边三角形,
∴AP=AC=
AB=2
.
24.
(1)解:如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)解:线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2
.
理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
∵在Rt△NFC中,CF2+CN2=NF2
,
∴EA2+CF2=EF2;
(3)解:如图3,延长GE,HF交于K,
由(2)知EA2+CF2=EF2
,
∴
EA2+
CF2=
EF2
,
∴S△AGE+S△CFH=S△EFK
,
∴S△AGE+S△CFH+S五边形BGEFH=S△EFK+S五边形BGEFH
,
即S△ABC=S矩形BGKH
,
∴
S△ABC=
S矩形BGKH
,
∴S△GBH=S△ABO=S△CBO
,
∴S△BGM=S四边形COMH
,
S△BMH=S四边形AGMO
,
∵S四边形AGMO:S四边形CHMO=8:9,
∴S△BMH:S△BGM=8:9,
∵BM平分∠GBH,
∴BG:BH=9:8,
设BG=9k,BH=8k,
∴CH=3+k,
∵AG=3,
∴AE=3
,
∴CF=
(k+3),EF=
(8k﹣3),
∵EA2+CF2=EF2
,
∴
,
整理得:7k2﹣6k﹣1=0,
解得:k1=﹣
(舍去),k2=1.
∴AB=12,
∴AO=
AB=6
,
∴⊙O的半径为6
.
测试卷解析版
一、选择题(共10题;共30分)
1.已知⊙O的半径为3,A为线段PO的中点,则当OP=5时,点A与⊙O的位置关系为( )
A.?点在圆内??B.?点在圆上????C.?点在圆外????D.?不能确定
2.在绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是(??
)
A.?????B.???????C.???????D.?
3.往直径为
的圆柱形容器内装入一些水以后,截面如图所示,若水面宽
,则水的最大深度为(???
)
A.??????B.?????C.?????D.?
4.如图,
是⊙O的直径,点C、D在⊙O上,
,则
的大小为(???
)
A.????B.?????C.?????D.?
5.如图,点A,B,C,D在⊙O上,
,点B是
的中点,则
的度数是(???
)
A.??????B.??????C.????D.?
6.如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE。若∠D=80°,则∠EAC的度数是(???
)
A.?20°????B.?25°????C.?30°????D.?35°
7.如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近(?
)
A.????????B.???????C.?????????D.?
8.如图,放置在直线l上的扇形OAB.由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的最短路径的长是(????
)
A.?2π+2????B.?3π???C.???????D.?
+2
9.如图,在扇形
中,已知
,
,过
的中点C作
,
,垂足分别为D、E,则图中阴影部分的面积为(??
)
A.???????B.??????C.??????D.?
10.如图,在平面直角坐标系中,Q是直线y=﹣
x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点
,连接
,则
的最小值为(???
)
A.?????B.???????C.?????????D.?
二、填空题(共6题;共24分)
11.在⊙O中,若弦
垂直平分半径
,则弦
所对的圆周角等于________°.
12.如图,AB为
的直径,弦
于点H
,
若
,
,则OH的长度为
________.
13.小明在手工制作课上,用面积为
,半径为
的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为________
.
14.如图,已知锐角三角形
内接于半径为2的
,
于点
,
,则
________.
15.如图,正方形
的边长为1,将其绕顶点C按逆时针方向旋转一定角度到
位置,使得点B落在对角线
上,则阴影部分的面积是________.
16.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为
,则半圆的半径OA的长为________.
三、解答题(共8题;共66分)
17.如图,在
中,
,将
绕点A逆时针旋转
,得到
,使得点B、C、D恰好在同一条直线上,求
的度数.
18.如图,△ABC的三个顶点都在⊙O上,直径AD=6cm
,
∠DAC=2∠B
,
求AC的长.
19.如图,△ABC中,AB=AC
,
⊙O是△ABC的外接圆,BO的延长交边AC于点D
.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小;
(3)当AD=2,CD=3时,求边BC的长.
20.如图,将
绕点B顺时针旋转60度得到
,点C的对应点E恰好落在AB的延长线上,连接AD.
(1)求证:
;
(2)若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.
21.如图,在
中,
,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作
,交⊙O于点F,求证:
(1)四边形DBCF是平行四边形
(2)
22.如图,点M,
分别在正方形
的边
,
上,且
,把
绕点A顺时针旋转
得到
.
(1)求证:
≌
.
(2)若
,
,求正方形
的边长.
23.如图所示,已知A
,
B两点的坐标分别为(2
,0),(0,10),P是△AOB外接圆⊙C上的一点,OP交AB于点
D
.
(1)当OP⊥AB时,求OP;
(2)当∠AOP=30°时,求AP
.
24.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;
(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.
答案
一、选择题
1.解:∵OA=
OP=2.5,⊙O的半径为3,
∴OA<⊙O半径,
∴点A与⊙O的位置关系为:点在圆内.故答案为:A.
2.解:ACD、
不是由某个基本图形经过旋转得到的,故ACD不符合题意;
B、是由一个基本图形经过旋转得到的,故B符合题意.
故答案为:B.
3.解:过点O作OD⊥AB于D,交⊙O于E,连接OA,
由垂径定理得:
,
∵⊙O的直径为
,
∴
,
在
中,由勾股定理得:
,
∴
,
∴油的最大深度为
,
故答案为:
.
4.解:∵∠BDC=20°
∴∠BOC=2×20°=40°
∴∠AOC=180°-40°=140°
故答案为:B.
5.连接OB,
∵点B是弧AC的中点,
∴∠AOB=
∠AOC=60°,
由圆周角定理得,∠D=
∠AOB=30°,
故答案为:A.
6.∵四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°-∠D)=50°,
∵四边形AECD是圆内接四边形,∠D=80°,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB-∠ACB=30°.
故答案为:C.
7.连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC=
AB=
a,
则正方形桌面与翻折成的圆形桌面的面积之比为:
,
故答案为:C.
8.解:如图,
?
点O的运动路径的长=
的长+O1O2+
的长=
+
+
=
,
故答案为:C.
9.连接OC
点C为弧AB的中点
在
和
中
又
四边形CDOE为正方形
由扇形面积公式得
故答案为:B.
10.解:作QM⊥x轴于点M,Q′N⊥x轴于N,
设Q(
,
),则PM=
,QM=
,
∵∠PMQ=∠PNQ′=∠QPQ′=90°,
∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,
∴∠QPM=∠PQ′N,
在△PQM和△Q′PN中,
,
∴△PQM≌△Q′PN(AAS),
∴PN=QM=
,Q′N=PM=
,
∴ON=1+PN=
,
∴Q′(
,
),
∴OQ′2=(
)2+(
)2=
m2﹣5m+10=
(m﹣2)2+5,
当m=2时,OQ′2有最小值为5,
∴OQ′的最小值为
,
故答案为:B.
二、填空题
11.设弦
垂直平分半径
于点E,连接OB、OC、AB、AC,且在优弧BC上取点F,连接BF、CF,
∴OB=AB,OC=AC,
∵OB=OC,
∴四边形OBAC是菱形,
∴∠BOC=2∠BOE,
∵OB=OA,OE=
,
∴cos∠BOE=
,
∴∠BOE=60°,
∴∠BOC=∠BAC=120°,
∴∠BFC=
∠BOC=60°,
∴
弦
所对的圆周角为120°或60°,
故答案为:120或60.
12.连接OC,
Rt△OCH中,OC=
AB=5,CH=
CD=4;
由勾股定理,得:OH=
;
即线段OH的长为3.
故答案为:3.
13.由
得:扇形的弧长=
(厘米),
圆锥的底面半径=
(厘米).
故答案是:10.
14.解:连接OB和OC,
∵△ABC内接于半径为2的圆O,∠BAC=60°,
∴∠BOC=120°,OB=OC=2,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,
∴∠OBD=30°,
∴OD=
OB=1,
故答案为:1.
15.解:过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=
EC=
,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴△PEC≌△PBC(HL),
∴PB=PE,
又∠PFB=45°,∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x
,
则EP=BP=
,
∵MP+BP=MB,
∴
,解得
,
∴BP=
,
∴阴影部分的面积=
.
故答案为:
.
16.解:如图,连接
?点C、D分别是半圆AOB上的三等分点,
?
?
为等边三角形,
?
?
?
?
?
解得:
(负根舍去),
故答案为:3
三、解答题
17.
解:∵将
绕点A逆时针旋转150°,得到
,
.
∵点B、C、D恰好在同一条直线上
是顶角为150°的等腰三角形,
,
,
.
18.
解:如图,连接OC
,
∵∠AOC=2∠B
,
∠DAC=2∠B
,
∴∠AOC=∠DAC
,
∴AO=AC
,
又∵OA=OC
,
∴△AOC是等边三角形,
∴AC=AO=
AD=3cm
.
19.
(1)连接OA,如下图1所示:
∵AB=AC,
∴
=
,
∴OA⊥BC,
∴∠BAO=∠CAO.
∵OA=OB,
∴∠ABD=∠BAO,
∴∠BAC=2∠ABD.
(2)如图2中,延长AO交BC于H.
①若BD=CB,则∠C=∠BDC=∠ABD+∠BAC=3∠ABD.
∵AB=AC,
∴∠ABC=∠C,
∴∠DBC=2∠ABD.
∵∠DBC+∠C+∠BDC=180°,
∴8∠ABD=180°,
∴∠C=3∠ABD=67.5°.
②若CD=CB,则∠CBD=∠CDB=3∠ABD,∴∠C=4∠ABD.
∵∠DBC+∠C+∠CDB=180°,
∴10∠ABD=180°,
∴∠BCD=4∠ABD=72°.
③若DB=DC,则D与A重合,这种情形不存在.
综上所述:∠C的值为67.5°或72°.
(3)如图3中,过A点作AE
BC交BD的延长线于E.
则
=
=
,且BC=2BH,
∴
=
=
,
设OB=OA=4a,OH=3a.
则在Rt△ABH和Rt△OBH中,
∵BH2=AB2﹣AH2=OB2﹣OH2
,
∴25
-
49a2=16a2﹣9a2
,
∴a2=
,
∴BH=
,
∴BC=2BH=
.
故答案为:
.
20.
(1)证明:由旋转性质得:
是等边三角形
所以
∴
;
(2)解:依题意得:AB=BD=4,BC=BE=1,
所以A,C两点经过的路径长之和为
.
21.
(1)证明:
,
,
,
,
又
,
?
?
四边形
是平行四边形.
(2)证明:如图,连接
,
四边形
是
的内接四边形
22.
(1)证明:由旋转的性质得:
四边形ABCD是正方形
,即
,即
在
和
中,
;
(2)解:设正方形
的边长为x,则
由旋转的性质得:
由(1)已证:
又
四边形ABCD是正方形
则在
中,
,即
解得
或
(不符题意,舍去)
故正方形
的边长为6.
23.
(1)解:∵A,B两点的坐标分别为(2
,0),(0,10),
∴AO=2
,OB=10,
∵AO⊥BO,
∴AB=
=4
,
∵OP⊥AB,
∴
=
,CD=DP,
∴CD=
,
∴OP=2CD=
;
(2)解:连接CP,如图所示:
∵∠AOP=30°,
∴∠ACP=60°,
∵CP=CA,
∴△ACP为等边三角形,
∴AP=AC=
AB=2
.
24.
(1)解:如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)解:线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2
.
理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
∵在Rt△NFC中,CF2+CN2=NF2
,
∴EA2+CF2=EF2;
(3)解:如图3,延长GE,HF交于K,
由(2)知EA2+CF2=EF2
,
∴
EA2+
CF2=
EF2
,
∴S△AGE+S△CFH=S△EFK
,
∴S△AGE+S△CFH+S五边形BGEFH=S△EFK+S五边形BGEFH
,
即S△ABC=S矩形BGKH
,
∴
S△ABC=
S矩形BGKH
,
∴S△GBH=S△ABO=S△CBO
,
∴S△BGM=S四边形COMH
,
S△BMH=S四边形AGMO
,
∵S四边形AGMO:S四边形CHMO=8:9,
∴S△BMH:S△BGM=8:9,
∵BM平分∠GBH,
∴BG:BH=9:8,
设BG=9k,BH=8k,
∴CH=3+k,
∵AG=3,
∴AE=3
,
∴CF=
(k+3),EF=
(8k﹣3),
∵EA2+CF2=EF2
,
∴
,
整理得:7k2﹣6k﹣1=0,
解得:k1=﹣
(舍去),k2=1.
∴AB=12,
∴AO=
AB=6
,
∴⊙O的半径为6
.
同课章节目录
