第1章 三角形的初步认识单元测试卷(含解析)
文档属性
| 名称 | 第1章 三角形的初步认识单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 545.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-28 16:48:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级上册数学
三角形的初步认识
单元测试卷
(满分100分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列命题中,是真命题的是( )
A.
若x2-x=0,则x=0
B.
面积相等的两个三角形全等
C.
三角形的三条高线相交于三角形内一点
D.
成轴对称的两个图形是全等图形
如下图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是(
)
A.
B.
C.
D.
如图,将矩形ABCD沿EF折叠,使点B,D重合,则下面三个结论:①DE=DF;②DF=EF;③△DCF≌△DGE中,正确的是(
)
A.
①②
B.
①③
C.
②③
D.
①②③
下列尺规作图的语句正确的是(
)
A.
延长射线AB到D
B.
延长线段AB至C,使AC=BC
C.
作直线AB=3cm
D.
以点D为圆心,任意长为半径画弧
现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根首尾顺次相接组成一个三角形,那么可以组成的三角形共有(
)
A.
1个
B.
2个
C.
3个
D.
4个
否定结论“至多有两个解”的说法中,正确的是(
)
A.
有一个解
B.
有两个解
C.
至少有三个解
D.
至少有两个解
如图,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连接BF,CE,则下列的结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③△ABD与△ACD的面积相等;④BF∥CE.
A.
1个
B.
2个
C.
3个
D.
4个
点D是AB上一点,AD=3BD,DF交AC于点E,DE=EF,FC∥AB,S△ABC=24,则△CEF的面积是( )
A.
6
B.
8
C.
9
D.
12
已知下列命题:若|x|=3,则x=3;当a>b时,若c>0,则ac>bc;若>,则m>n;内错角相等.其中原命题与逆命题均为真命题的个数是(?
?
?
)
A.
1
B.
2
C.
3
D.
4
如图,在△ABC中,AD是△ABC的外角平分线,点P是AD上异于点A的任意一点,设PBm,PCn,AB,AC,则(???
)
A.
B.
C.
D.
无法判断
二、填空题(本大题共10小题,共30.0分)
造房子时屋顶常用三角结构,是应用了______
;而活动挂架则用了四边形的______
.
命题“对顶角相等”是
________命题,用“如果…那么…”的形式改写________
已知三角形的三边长分别为2,a-1,4,则化简的结果为____
?
?____.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠ADE=
??°;
如图:△ABC中,∠A
=
30°,∠B
=
70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于D,则∠CDF=___________°.
如图,在△ABC中,∠A=
,BD平分∠ABC,且∠C=3∠CBD,则∠CDB=??????????.
如图,在折纸活动中,小明制作了一张纸片,点分别在边上,将沿着折叠压平,点落在处.若
,
则
??????.
在△ACB中,∠C=90°,AC=BC,点O为AB的中点,若点M在边AC上,点N在边BC的延长线上,满足:MN-AM=CN,则∠MON=______.
如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为36,则阴影部分的面积为______.
如图,锐角△ABC的高AD,BE相交于F,若BF=AC,BC=7,DF=2,则S△ADC
=_________.
三、解答题(本大题共7小题,共40.0分)
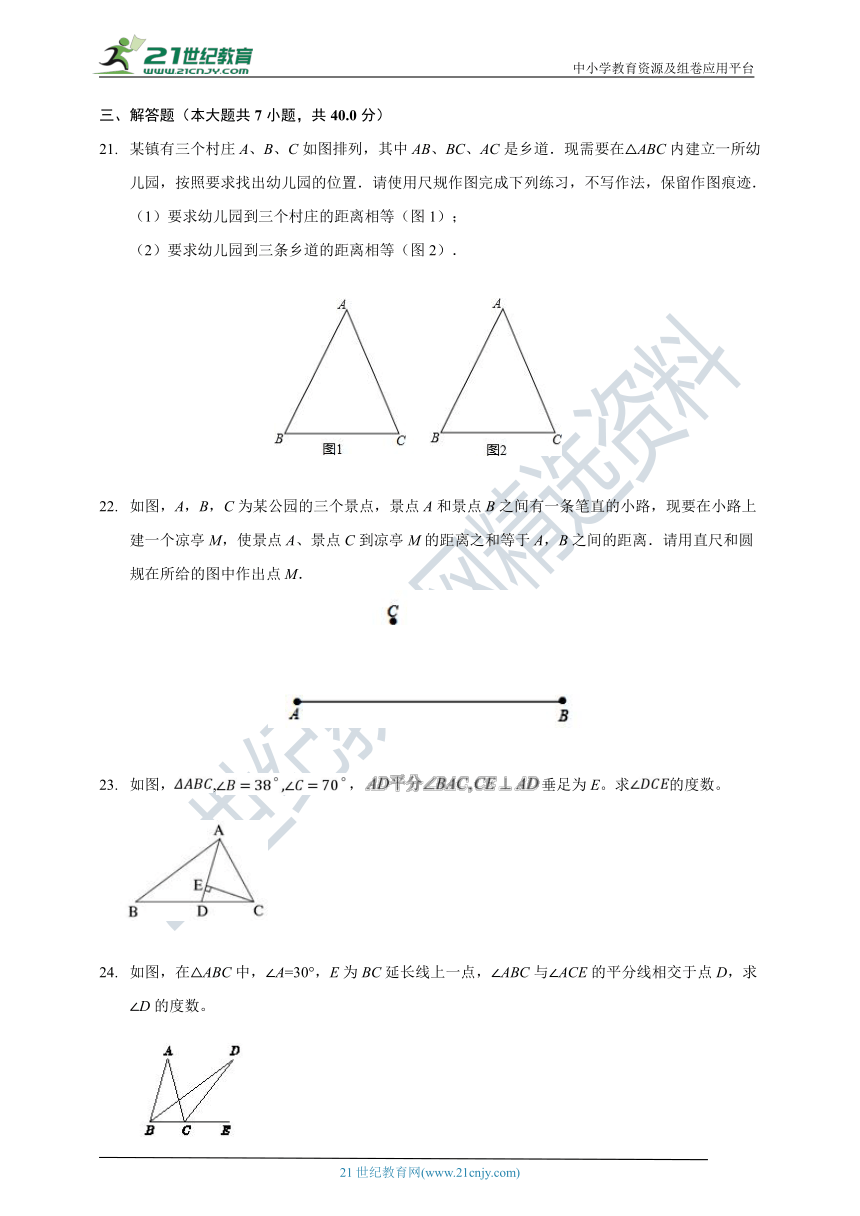
某镇有三个村庄A、B、C如图排列,其中AB、BC、AC是乡道.现需要在△ABC内建立一所幼儿园,按照要求找出幼儿园的位置.请使用尺规作图完成下列练习,不写作法,保留作图痕迹.
(1)要求幼儿园到三个村庄的距离相等(图1);
(2)要求幼儿园到三条乡道的距离相等(图2).
如图,A,B,C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭M,使景点A、景点C到凉亭M的距离之和等于A,B之间的距离.请用直尺和圆规在所给的图中作出点M.
如图,,,垂足为E。求的度数。
如图,在△ABC中,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,求∠D的度数。
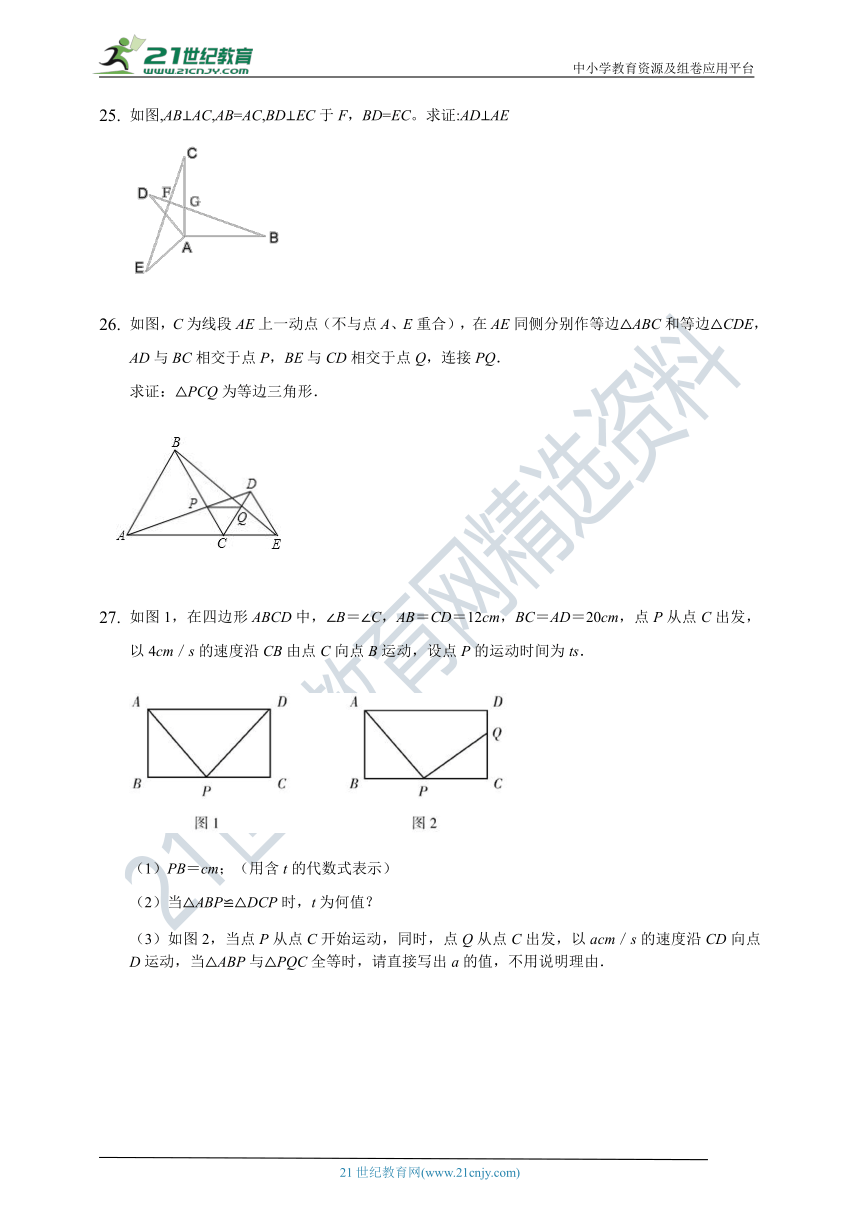
如图,AB⊥AC,AB=AC,BD⊥EC于F,BD=EC。求证:AD⊥AE
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
求证:△PCQ为等边三角形.
如图1,在四边形ABCD中,∠B=∠C,AB=CD=12cm,BC=AD=20cm,点P从点C出发,以4cm/s的速度沿CB由点C向点B运动,设点P的运动时间为ts.
(1)PB=cm;(用含t的代数式表示)
(2)当△ABP≌△DCP时,t为何值?
(3)如图2,当点P从点C开始运动,同时,点Q从点C出发,以acm/s的速度沿CD向点D运动,当△ABP与△PQC全等时,请直接写出a的值,不用说明理由.
答案和解析
1.【答案】D
2.【答案】B
【解析】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.根据全等三角形的判定方法进行逐个验证,做题时要找准对应边,对应角.
3.【答案】B
【解析】本题考查翻折变换、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,属于中考常考题型.如图作EM⊥BC于M,首先证明△DEG≌△DFC,由此可以判断①③正确.设②错误,可以用反证法证明.
解:如图作EM⊥BC于M.
∵四边形ABCD是矩形,四边形EFDG是由四边形ABEF翻折,
∴∠ADC=∠GDF=∠C=∠G=90°,DC=DG=AB,AD=BC,
∴∠EDG=∠CDF,
在△DEG和△DFC中,
,
∴△DEG≌△DFC,故③正确,
∴DE=DF,故①正确,
②错误.假设DF=EF,∵DE=DF,
∴EF=DE=DF,
∴△DEF是等边三角形,
∴∠DFE=60°,
∴∠BFE=∠DFE=∠DFC=60°,
这显然不一定成立,假设不成立,故②错误.
4.【答案】D
【解析】A.延长射线AB到D,错误,射线不能延长;
B.延长线段AB至C,使AC=BC,是辅助线的方法,故错误;
C.作直线AB=3cm,直线没有长度,故错误;
D.以点D为圆心,任意长为半径画弧,正确.
5.【答案】B
6.【答案】C
【解析】本题考查的知识是命题的否定,其中熟练掌握多性问题的否定思路:至多n个的否定为至少n+1个,是解答本题的关键.?
7.【答案】D
8.【答案】C
【解析】连接BE.
∵FC∥AB,
∴∠ADF=∠F.
∵∠AED=∠CEF,DE=EF,
∴△ADE≌△CEF.
∴AE=CE.
即E是AC的中点.
∵S△ABC=24,
∴S△ABE=12,
∵AD=3BD,
∴S△ADE=×12=9,
∴S△EFC=S△ADE=9,
本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
9.【答案】A
【解析】本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,把一个命题的条件和结论互换就得到它的逆命题.
若|x|=3,则x=3为假命题,其逆命题为真命题;
当a>b时,若c>0,则ac>bc为真命题,其逆命题为真命题;
若>,则m>n为真命题,其逆命题为假命题;
内错角相等为假命题,其逆命题为假命题.
10.【答案】A
【解析】本题主要考查三角形全等的证明,全等三角形的性质,三角形的三边关系,作辅助线构造以m、n、b、c的长度为边的三角形是解题的关键,也是解本题的难点.在BA的延长线上取点E,使AE=AC,连接EP,证明△ACP和△AEP全等,推出PE=PC,根据三角形任意两边之和大于第三边即可得到m+n>b+c,即大于1.
11.【答案】三角形的稳定性;不稳定性
12.【答案】真;如果两个角是对顶角,那么它们相等.
13.【答案】4
【解析】本题考查了三角形三边关系和绝对值化简,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求a的取值范围;再把绝对值化简.
14.【答案】42
【解析】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.先根据三角形内角和定理计算出∠B=66°,再根据折叠的性质得∠DEC=∠B=66°,然后根据三角形外角性质求∠ADE的度数.
15.【答案】70
【解析】本题主要考查了三角形的内角和定理,角平分线的定义,垂直的定义.根据三角形内角和定理得到∠ACB=80°,再根据角平分线的定义得到∠BCE=40°,根据垂直的定义得到∠BDC=∠DFC=90°,进而得到∠BCD=20°,∠FCD=20°,从而得到答案.
16.【答案】108°
【解析】本题考查了三角形的内角和定理以及角平分线的定义,首先根据直角三角形的两锐角互余得到∠ABC+∠C=90°,然后根据角平分线定义和三角形内角和定理得出∠CDB的度数即可.
17.【答案】150°
【解析】本题考查了三角形的内角和定理,翻折变换的性质,整体思想的利用求解更简便.根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠A′DE=∠ADE,∠A′ED=∠AED,然后利用平角等于180°列式计算即可得解.
18.【答案】45°
【解析】解:∵∠ACB=90°,点O为AB的中点
∴CO=AB=BO;
在线段BC上取点H,使CH=AM,连接OH,如图所示:
∵∠ACB=90°,AO=BO,
∴∠A=∠B=45°,∠ACO=∠BCO=45°,
在△AOM和△COH中,,
∴△AOM≌△COH(SAS)
∴OM=OH,
∵MN-AM=CN,∴NM=NH,
在△MON和△HON中,,
∴△MON≌△HON(SSS),
∴∠MON=∠HON,∴∠MON=∠MOH=∠AOC=45°
本题考查的是全等三角形的判定和性质,等腰直角三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.
19.【答案】612
【解析】分别连接AF、DC、EB.
∵△DFA与△BFA等底同高,
∴S△DAF=S△BAF.
∵△ABC与△ACD等底同高,
∴S△ABC=S△ACD=36.
∴S△BDC=72,
∵CE=2AC.BF=3BC
∴S△DEC=2S△ACD=72,S△BAF=3S△ABC=108,S△BEC=2S△ABC=72,S△BEF=3S△BEC=216,S△DAF=108,
∴阴影部分的面积=S△BAF+S△DAF+S△ACD+S△DEC+S△BEC+S△BEF=612.
此题主要考查学生对三角形面积的理解和掌握,解答此题的关键是分别连接AF、DC、EB,求出各三角形的面积.
20.【答案】5
【解析】此题考查三角形全等的判断及性质,考查三角形的面积,关键是利用全等三角形得出边DC与FD.
解:因为锐角△ABC的高AD,BE相交于F,
所以,
则,
又BF=AC,,
所以△FDB≌△CDA,
则CD=DF=2,DA=BD=7-2=5,
所以.
21.【答案】(1)如图1:
(2)如图2:
【解析】(1)幼儿园的位置按照设计要求,在△ABC的内部,且到A、B、C的距离必须相等,因此确定幼儿园的位置在线段AB、AC、BC的垂直平分线上,由此确定幼儿园的位置是三边垂直平分线的交点.
(2)幼儿园的位置按照设计要求,在△ABC的内部,且到AB、AC、BC的距离必须相等,因此确定幼儿园的位置在三角形三角的平分线上,由此确定幼儿园的位置是三角平分线的交点.
此题主要考查了线段的垂直平分线的性质和角平分线的性质,由已知能够确定点P、Q具有的性质是解决问题的关键.
22.【答案】如图所示,点M即为所求:
理由:∵DE垂直平分线段BC,
∴MC=MB,
∴AM+CM=AM+BM=AB,
即景点A、景点C到凉亭M的距离之和等于A,B之间的距离.
【解析】本题考查应用与设计作图、线段的垂直平分线的性质等知识,首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.连接BC,作BC中垂线与AB交点即为M.
23.【答案】解:∵∠B=38°,∠ACB=70°,
∴∠BAC=180°-38°-70°=72°,
∵AD平分∠BAC,∴,
∵CE⊥AD,∴∠AEC=∠DEC=90°,
∴∠ACE=90°-36°=54°,
∴∠DCE=70°-54°=16°.
即∠DCE的度数是16°.
【解析】本题主要考查了三角形的内角和定理以及角平分线的定义,难度适中.
根据三角形的内角和定理可知∠BAC的度数,再根据角平分线以及垂直的性质可求出∠ACE的度数,继而得出∠DCE的度数.
24.【答案】解:∵∠ABC的平分线与∠ACE的平分线交于点D
∴∠ABD=∠CBD=∠ABC,∠ACD=∠ECD=∠ACE,
∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,
∴∠ACE=∠A+∠ABC,即:∠ECD=∠A+∠CBD,
∵∠DCE是△DBC的外角,∴∠DCE=∠D+∠DBC,
∴∠D=∠A=×30°=15°.
【解析】本题考查三角形的外角的性质,角平分线的定义.先根据角平分线的定义分别求出∠CBD=∠ABC,∠ECD=∠ACE,再根据∠ACE、∠ECD分别是△ABC和△DBC的外角,等于和它不相邻的两个内角的和,得出∠D=∠A,从而求出∠D的度数.
25.【答案】解:∵AB⊥AC,∴∠BAC=90°,
∵∠AGB=∠CGF,BD⊥EC于F,
∴∠BAC=∠CFG=90°
∴∠B=∠C,
在△CAE与△BAD中,
AC=AB,∠C=∠B,CE=BD,
∴△CAE≌△BAD,
∴∠CAE=∠BAD,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠DAE=∠BAC=90°,
∴AD⊥AE.
【解析】本题主要考查了全等三角形的判定与性质,首先由SAS可推△CAE≌△BAD,得到∠CAE=∠BAD,进而得到∠DAE=∠BAC,由AB⊥AC可推∠BAC=90°,从而有∠DAE=90°,由此即可得证.
26.【答案】证明:∵△ABC和△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
在△ACP和△BCq中,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
∴△PCQ为等边三角形.
【解析】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
27.【答案】解:(1)(20-4t);
(2)∵△ABP≌△DCP,
∴BP=CP,
∴20-4t=4t,解得t=2.5
(3)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=12cm,∴PC=12cm,∴BP=20-12=8cm,
∴4t=12,解得:t=3,
CQ=BP=8cm,cm/s;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∴cm,
4t=10,解得:t=2.5,
CQ=AB=12cm,a=4.8cm/s.
综上所述:当cm/s或4.8cm/s时△ABP与△PQC全等.
【解析】此题主要考查了全等三角形的判定,关键是掌握全等三角形全等的条件,找准对应边.
(1)根据P点的运动速度可得PC的长,再利用BC-PC即可得到PB的长;
(2)因为△ABP≌△DCP,所以当BP=CP时,据此即可解答;
(3)此题主要分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到a的值.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
八年级上册数学
三角形的初步认识
单元测试卷
(满分100分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列命题中,是真命题的是( )
A.
若x2-x=0,则x=0
B.
面积相等的两个三角形全等
C.
三角形的三条高线相交于三角形内一点
D.
成轴对称的两个图形是全等图形
如下图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是(
)
A.
B.
C.
D.
如图,将矩形ABCD沿EF折叠,使点B,D重合,则下面三个结论:①DE=DF;②DF=EF;③△DCF≌△DGE中,正确的是(
)
A.
①②
B.
①③
C.
②③
D.
①②③
下列尺规作图的语句正确的是(
)
A.
延长射线AB到D
B.
延长线段AB至C,使AC=BC
C.
作直线AB=3cm
D.
以点D为圆心,任意长为半径画弧
现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根首尾顺次相接组成一个三角形,那么可以组成的三角形共有(
)
A.
1个
B.
2个
C.
3个
D.
4个
否定结论“至多有两个解”的说法中,正确的是(
)
A.
有一个解
B.
有两个解
C.
至少有三个解
D.
至少有两个解
如图,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连接BF,CE,则下列的结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③△ABD与△ACD的面积相等;④BF∥CE.
A.
1个
B.
2个
C.
3个
D.
4个
点D是AB上一点,AD=3BD,DF交AC于点E,DE=EF,FC∥AB,S△ABC=24,则△CEF的面积是( )
A.
6
B.
8
C.
9
D.
12
已知下列命题:若|x|=3,则x=3;当a>b时,若c>0,则ac>bc;若>,则m>n;内错角相等.其中原命题与逆命题均为真命题的个数是(?
?
?
)
A.
1
B.
2
C.
3
D.
4
如图,在△ABC中,AD是△ABC的外角平分线,点P是AD上异于点A的任意一点,设PBm,PCn,AB,AC,则(???
)
A.
B.
C.
D.
无法判断
二、填空题(本大题共10小题,共30.0分)
造房子时屋顶常用三角结构,是应用了______
;而活动挂架则用了四边形的______
.
命题“对顶角相等”是
________命题,用“如果…那么…”的形式改写________
已知三角形的三边长分别为2,a-1,4,则化简的结果为____
?
?____.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠ADE=
??°;
如图:△ABC中,∠A
=
30°,∠B
=
70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于D,则∠CDF=___________°.
如图,在△ABC中,∠A=
,BD平分∠ABC,且∠C=3∠CBD,则∠CDB=??????????.
如图,在折纸活动中,小明制作了一张纸片,点分别在边上,将沿着折叠压平,点落在处.若
,
则
??????.
在△ACB中,∠C=90°,AC=BC,点O为AB的中点,若点M在边AC上,点N在边BC的延长线上,满足:MN-AM=CN,则∠MON=______.
如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为36,则阴影部分的面积为______.
如图,锐角△ABC的高AD,BE相交于F,若BF=AC,BC=7,DF=2,则S△ADC
=_________.
三、解答题(本大题共7小题,共40.0分)
某镇有三个村庄A、B、C如图排列,其中AB、BC、AC是乡道.现需要在△ABC内建立一所幼儿园,按照要求找出幼儿园的位置.请使用尺规作图完成下列练习,不写作法,保留作图痕迹.
(1)要求幼儿园到三个村庄的距离相等(图1);
(2)要求幼儿园到三条乡道的距离相等(图2).
如图,A,B,C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭M,使景点A、景点C到凉亭M的距离之和等于A,B之间的距离.请用直尺和圆规在所给的图中作出点M.
如图,,,垂足为E。求的度数。
如图,在△ABC中,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,求∠D的度数。
如图,AB⊥AC,AB=AC,BD⊥EC于F,BD=EC。求证:AD⊥AE
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
求证:△PCQ为等边三角形.
如图1,在四边形ABCD中,∠B=∠C,AB=CD=12cm,BC=AD=20cm,点P从点C出发,以4cm/s的速度沿CB由点C向点B运动,设点P的运动时间为ts.
(1)PB=cm;(用含t的代数式表示)
(2)当△ABP≌△DCP时,t为何值?
(3)如图2,当点P从点C开始运动,同时,点Q从点C出发,以acm/s的速度沿CD向点D运动,当△ABP与△PQC全等时,请直接写出a的值,不用说明理由.
答案和解析
1.【答案】D
2.【答案】B
【解析】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.根据全等三角形的判定方法进行逐个验证,做题时要找准对应边,对应角.
3.【答案】B
【解析】本题考查翻折变换、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,属于中考常考题型.如图作EM⊥BC于M,首先证明△DEG≌△DFC,由此可以判断①③正确.设②错误,可以用反证法证明.
解:如图作EM⊥BC于M.
∵四边形ABCD是矩形,四边形EFDG是由四边形ABEF翻折,
∴∠ADC=∠GDF=∠C=∠G=90°,DC=DG=AB,AD=BC,
∴∠EDG=∠CDF,
在△DEG和△DFC中,
,
∴△DEG≌△DFC,故③正确,
∴DE=DF,故①正确,
②错误.假设DF=EF,∵DE=DF,
∴EF=DE=DF,
∴△DEF是等边三角形,
∴∠DFE=60°,
∴∠BFE=∠DFE=∠DFC=60°,
这显然不一定成立,假设不成立,故②错误.
4.【答案】D
【解析】A.延长射线AB到D,错误,射线不能延长;
B.延长线段AB至C,使AC=BC,是辅助线的方法,故错误;
C.作直线AB=3cm,直线没有长度,故错误;
D.以点D为圆心,任意长为半径画弧,正确.
5.【答案】B
6.【答案】C
【解析】本题考查的知识是命题的否定,其中熟练掌握多性问题的否定思路:至多n个的否定为至少n+1个,是解答本题的关键.?
7.【答案】D
8.【答案】C
【解析】连接BE.
∵FC∥AB,
∴∠ADF=∠F.
∵∠AED=∠CEF,DE=EF,
∴△ADE≌△CEF.
∴AE=CE.
即E是AC的中点.
∵S△ABC=24,
∴S△ABE=12,
∵AD=3BD,
∴S△ADE=×12=9,
∴S△EFC=S△ADE=9,
本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
9.【答案】A
【解析】本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,把一个命题的条件和结论互换就得到它的逆命题.
若|x|=3,则x=3为假命题,其逆命题为真命题;
当a>b时,若c>0,则ac>bc为真命题,其逆命题为真命题;
若>,则m>n为真命题,其逆命题为假命题;
内错角相等为假命题,其逆命题为假命题.
10.【答案】A
【解析】本题主要考查三角形全等的证明,全等三角形的性质,三角形的三边关系,作辅助线构造以m、n、b、c的长度为边的三角形是解题的关键,也是解本题的难点.在BA的延长线上取点E,使AE=AC,连接EP,证明△ACP和△AEP全等,推出PE=PC,根据三角形任意两边之和大于第三边即可得到m+n>b+c,即大于1.
11.【答案】三角形的稳定性;不稳定性
12.【答案】真;如果两个角是对顶角,那么它们相等.
13.【答案】4
【解析】本题考查了三角形三边关系和绝对值化简,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求a的取值范围;再把绝对值化简.
14.【答案】42
【解析】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.先根据三角形内角和定理计算出∠B=66°,再根据折叠的性质得∠DEC=∠B=66°,然后根据三角形外角性质求∠ADE的度数.
15.【答案】70
【解析】本题主要考查了三角形的内角和定理,角平分线的定义,垂直的定义.根据三角形内角和定理得到∠ACB=80°,再根据角平分线的定义得到∠BCE=40°,根据垂直的定义得到∠BDC=∠DFC=90°,进而得到∠BCD=20°,∠FCD=20°,从而得到答案.
16.【答案】108°
【解析】本题考查了三角形的内角和定理以及角平分线的定义,首先根据直角三角形的两锐角互余得到∠ABC+∠C=90°,然后根据角平分线定义和三角形内角和定理得出∠CDB的度数即可.
17.【答案】150°
【解析】本题考查了三角形的内角和定理,翻折变换的性质,整体思想的利用求解更简便.根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠A′DE=∠ADE,∠A′ED=∠AED,然后利用平角等于180°列式计算即可得解.
18.【答案】45°
【解析】解:∵∠ACB=90°,点O为AB的中点
∴CO=AB=BO;
在线段BC上取点H,使CH=AM,连接OH,如图所示:
∵∠ACB=90°,AO=BO,
∴∠A=∠B=45°,∠ACO=∠BCO=45°,
在△AOM和△COH中,,
∴△AOM≌△COH(SAS)
∴OM=OH,
∵MN-AM=CN,∴NM=NH,
在△MON和△HON中,,
∴△MON≌△HON(SSS),
∴∠MON=∠HON,∴∠MON=∠MOH=∠AOC=45°
本题考查的是全等三角形的判定和性质,等腰直角三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.
19.【答案】612
【解析】分别连接AF、DC、EB.
∵△DFA与△BFA等底同高,
∴S△DAF=S△BAF.
∵△ABC与△ACD等底同高,
∴S△ABC=S△ACD=36.
∴S△BDC=72,
∵CE=2AC.BF=3BC
∴S△DEC=2S△ACD=72,S△BAF=3S△ABC=108,S△BEC=2S△ABC=72,S△BEF=3S△BEC=216,S△DAF=108,
∴阴影部分的面积=S△BAF+S△DAF+S△ACD+S△DEC+S△BEC+S△BEF=612.
此题主要考查学生对三角形面积的理解和掌握,解答此题的关键是分别连接AF、DC、EB,求出各三角形的面积.
20.【答案】5
【解析】此题考查三角形全等的判断及性质,考查三角形的面积,关键是利用全等三角形得出边DC与FD.
解:因为锐角△ABC的高AD,BE相交于F,
所以,
则,
又BF=AC,,
所以△FDB≌△CDA,
则CD=DF=2,DA=BD=7-2=5,
所以.
21.【答案】(1)如图1:
(2)如图2:
【解析】(1)幼儿园的位置按照设计要求,在△ABC的内部,且到A、B、C的距离必须相等,因此确定幼儿园的位置在线段AB、AC、BC的垂直平分线上,由此确定幼儿园的位置是三边垂直平分线的交点.
(2)幼儿园的位置按照设计要求,在△ABC的内部,且到AB、AC、BC的距离必须相等,因此确定幼儿园的位置在三角形三角的平分线上,由此确定幼儿园的位置是三角平分线的交点.
此题主要考查了线段的垂直平分线的性质和角平分线的性质,由已知能够确定点P、Q具有的性质是解决问题的关键.
22.【答案】如图所示,点M即为所求:
理由:∵DE垂直平分线段BC,
∴MC=MB,
∴AM+CM=AM+BM=AB,
即景点A、景点C到凉亭M的距离之和等于A,B之间的距离.
【解析】本题考查应用与设计作图、线段的垂直平分线的性质等知识,首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.连接BC,作BC中垂线与AB交点即为M.
23.【答案】解:∵∠B=38°,∠ACB=70°,
∴∠BAC=180°-38°-70°=72°,
∵AD平分∠BAC,∴,
∵CE⊥AD,∴∠AEC=∠DEC=90°,
∴∠ACE=90°-36°=54°,
∴∠DCE=70°-54°=16°.
即∠DCE的度数是16°.
【解析】本题主要考查了三角形的内角和定理以及角平分线的定义,难度适中.
根据三角形的内角和定理可知∠BAC的度数,再根据角平分线以及垂直的性质可求出∠ACE的度数,继而得出∠DCE的度数.
24.【答案】解:∵∠ABC的平分线与∠ACE的平分线交于点D
∴∠ABD=∠CBD=∠ABC,∠ACD=∠ECD=∠ACE,
∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,
∴∠ACE=∠A+∠ABC,即:∠ECD=∠A+∠CBD,
∵∠DCE是△DBC的外角,∴∠DCE=∠D+∠DBC,
∴∠D=∠A=×30°=15°.
【解析】本题考查三角形的外角的性质,角平分线的定义.先根据角平分线的定义分别求出∠CBD=∠ABC,∠ECD=∠ACE,再根据∠ACE、∠ECD分别是△ABC和△DBC的外角,等于和它不相邻的两个内角的和,得出∠D=∠A,从而求出∠D的度数.
25.【答案】解:∵AB⊥AC,∴∠BAC=90°,
∵∠AGB=∠CGF,BD⊥EC于F,
∴∠BAC=∠CFG=90°
∴∠B=∠C,
在△CAE与△BAD中,
AC=AB,∠C=∠B,CE=BD,
∴△CAE≌△BAD,
∴∠CAE=∠BAD,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠DAE=∠BAC=90°,
∴AD⊥AE.
【解析】本题主要考查了全等三角形的判定与性质,首先由SAS可推△CAE≌△BAD,得到∠CAE=∠BAD,进而得到∠DAE=∠BAC,由AB⊥AC可推∠BAC=90°,从而有∠DAE=90°,由此即可得证.
26.【答案】证明:∵△ABC和△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
在△ACP和△BCq中,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
∴△PCQ为等边三角形.
【解析】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
27.【答案】解:(1)(20-4t);
(2)∵△ABP≌△DCP,
∴BP=CP,
∴20-4t=4t,解得t=2.5
(3)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=12cm,∴PC=12cm,∴BP=20-12=8cm,
∴4t=12,解得:t=3,
CQ=BP=8cm,cm/s;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∴cm,
4t=10,解得:t=2.5,
CQ=AB=12cm,a=4.8cm/s.
综上所述:当cm/s或4.8cm/s时△ABP与△PQC全等.
【解析】此题主要考查了全等三角形的判定,关键是掌握全等三角形全等的条件,找准对应边.
(1)根据P点的运动速度可得PC的长,再利用BC-PC即可得到PB的长;
(2)因为△ABP≌△DCP,所以当BP=CP时,据此即可解答;
(3)此题主要分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到a的值.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
