人教版高中生物必修三4.2种群数量的变化(共26张PPT)
文档属性
| 名称 | 人教版高中生物必修三4.2种群数量的变化(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2020-08-28 15:36:45 | ||
图片预览





文档简介
(共26张PPT)
本节聚焦
一、建构种群增长模型的方法
二、种群增长的“J”型曲线
三、种群增长的“S”型曲线
四、种群数量的波动和下降
五、研究种群数量变化的意义
假设张翰承包了一个鱼塘养鱼虾,如果一次投放的幼苗过多或延迟捕捞,由于环境的负载能力限制,都不能达到效益的最优化;相反,如果大量捕捞,使鱼虾数量大大减少,其种群往往要经过相当长的延滞期才能进入指数增长期,对生产极为不利。那什么时候是捕捞的最佳数量期?
问题:如何合理利用和保护生物资源?
问题:种群的数量变化有怎样的规律?
问题的提出
数学模型:
是用来描述一个系统或它的性质的数学形式。
数学模型的表现形式可以为公式、图表等形式。
一、建构种群增长模型的方法
描述、解释和预测种群数量的变化,常常需要建立数学模型。
一、建构种群增长模型的方法
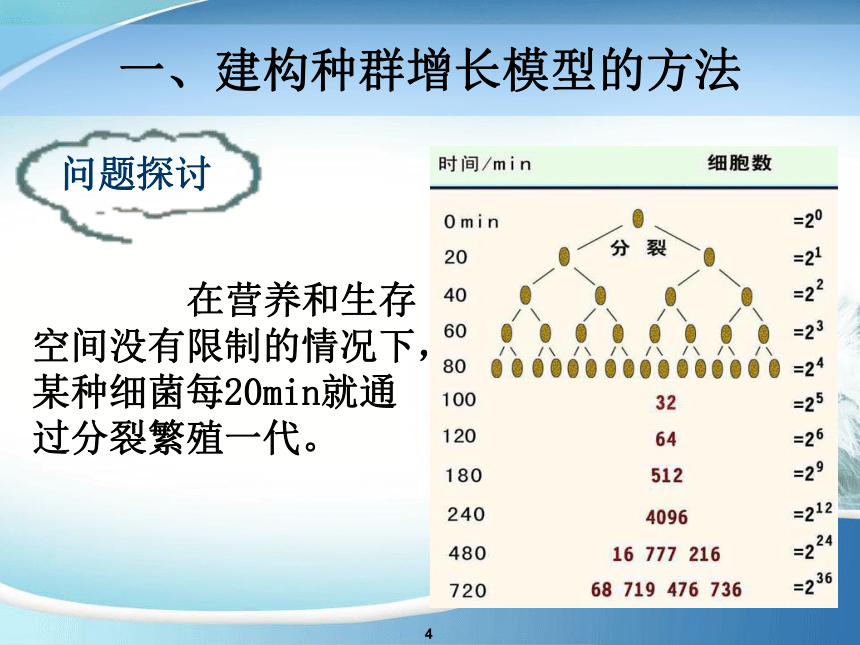
问题探讨
在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
一、建构种群增长模型的方法
时间(min)
20
40
60
80
100
120
140
160
180
分裂次数
数量(个)
2
4
8
16
32
64
128
256
512
1
2
3
4
5
6
7
8
9
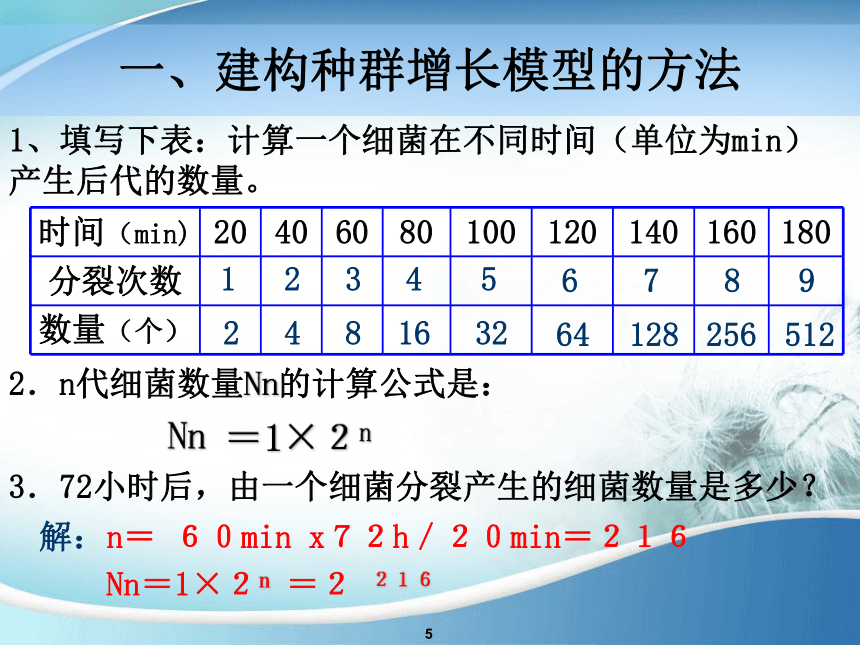
1、填写下表:计算一个细菌在不同时间(单位为min)产生后代的数量。
2.n代细菌数量Nn的计算公式是:
Nn
3.72小时后,由一个细菌分裂产生的细菌数量是多少?
=1×2n
解:n=
60min
x72h/20min=216
Nn=1×2n
=2
216
细菌数量
一、建构种群增长模型的方法
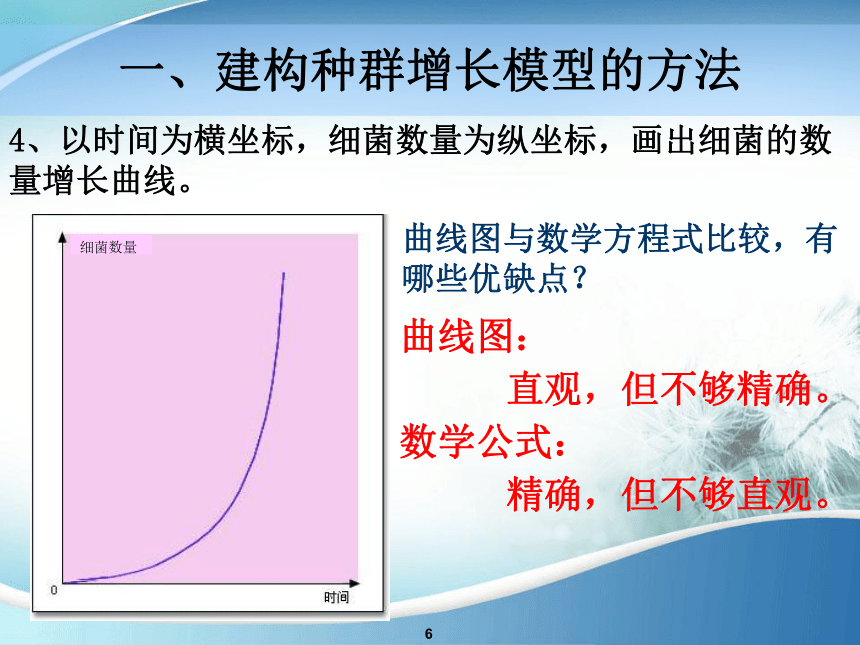
4、以时间为横坐标,细菌数量为纵坐标,画出细菌的数量增长曲线。
曲线图与数学方程式比较,有哪些优缺点?
曲线图:
直观,但不够精确。
数学公式:
精确,但不够直观。
一、建构种群增长模型的方法
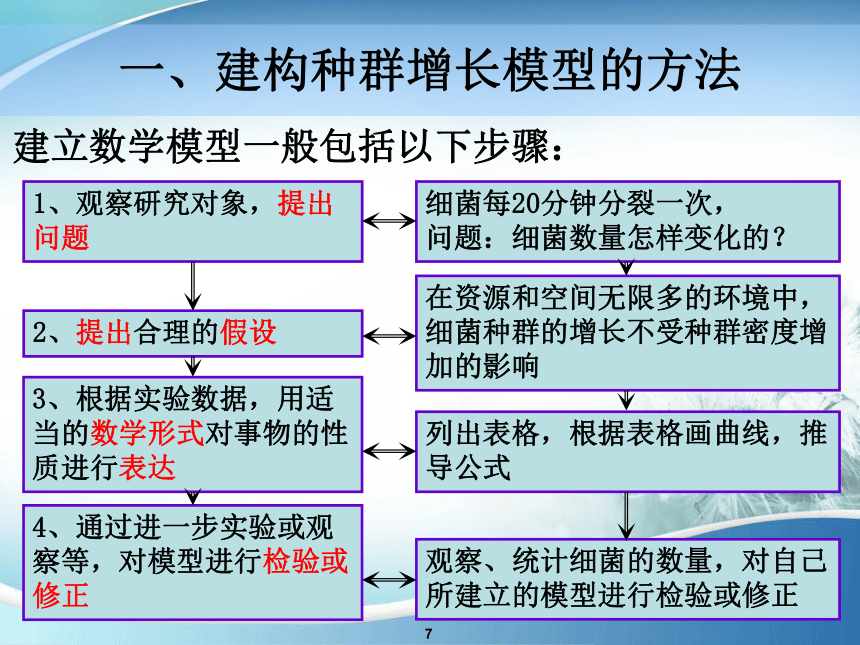
1、观察研究对象,提出问题
细菌每20分钟分裂一次,
问题:细菌数量怎样变化的?
2、提出合理的假设
在资源和空间无限多的环境中,细菌种群的增长不受种群密度增加的影响
3、根据实验数据,用适当的数学形式对事物的性质进行表达
列出表格,根据表格画曲线,推导公式
4、通过进一步实验或观察等,对模型进行检验或修正
观察、统计细菌的数量,对自己所建立的模型进行检验或修正
建立数学模型一般包括以下步骤:
实例一:1859年,一位英国人来到澳大利亚定居,他带来了24只野兔。让他没有想到的是,一个世纪之后,这24只野兔的后代竟达到6亿只以上。漫山遍野的野兔与牛羊争食牧草,啃啮树皮,造成植被破坏,导致水土流失。后来,人们引入了黏液瘤病毒才使野兔的数量得到控制。
实例二:凤眼莲原产于南美,仅以一种观赏性植物零散分布,1844年在美国的博览会上曾被喻为“美化世界的淡紫色花冠”。自此以后凤眼莲被作为观赏植物引种栽培,现已在亚、非、欧、北美洲等数十个国家造成危害。1901年作为花卉引入中国,30年代作为畜禽饲料引入中国内地各省,并作为观赏和净化水质的植物推广种植,后逃逸为野生。由于繁殖迅速,又几乎没有竞争对手和天敌
,在我国南方江河湖泊中发展迅速,目前我国有这种凤眼莲184万吨,成为我国淡水水体中主要的外来入侵物种之一。
实例三:在20世纪30年代,人们将环颈雉引入美国的一个岛屿。在1937-1942年期间,这个种群数量的增长如下图所示。
如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈什么型?
二、种群增长的“J”型曲线
①产生条件:
理想状态——食物充足,空间不限,
气候适宜,没有天敌等;
②增长特点:
种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
③量的计算:t年后种群的数量为
Nt=N0
λt
(N0为起始数量,
t为时间,Nt表示t年后该种群的数量,λ为年均增长率.)
④例子:实验室条件下、外来物种入侵、
迁移入新环境。
当种群数量呈现增长趋势时,能否通过该数学模型得出种群数量增长率的变化规律?
增长率始终为“λ-1”
λ-1
增长率是指在一段时间内,结束时种群数量相对于初始种群数量的增加部分占初始数量的比例。
问题探讨
在一个培养基中,细菌的数量会一直按照这个公式增长吗?为什么?
如何验证这个观点?
不会。原因是资源和空间是有限的。
生态学家高斯曾经做过这样一个实验:在0.5ml培养液中放入5个大草履虫,然后每隔24h统计一次大草履虫的数量。经过反复实验,得出了如图所示的结果。
思考:
1、曲线形状象什么?其种群达到基本稳定的数量值称为什么?
“S”型曲线
2、大草履虫数量增长过程如何?
三、种群增长的“S”型曲线
K值
种群增长速率不断降低
种群数量K/2
→K值时,
三、种群增长的“S”型曲线
种群数量达到K值时,
种群增长速率为零,但种群数量达到最大,且种内斗争最剧烈。
种群数量在
K/2值时,
种群增长速率最大
种群数量由0→K/2值时,
种群增长率速增大
K值:在环境条件不受破坏的情况下,一定空间中所能维持的种群最大数量称为环境容纳量。
K/2
转折期,增长速率最快
K值:环境容纳量
加速期,个体数量增加,增长加速
潜伏期,个体数量较少增长缓慢
减速期,增长缓慢
饱和期,增长速率为零
种
群
数
量
“S”
型
增
长
曲
线
(种群数量)
K/2
K
种
群
数
量
增
长
速率
时间
D:
种群数量处于K值,
增长率为0
B:
种群数量处于K/2值,
种群增长率最大
增长速率随时间变化曲线
B
D
讨论:
1、同一种群的K值是固定不变的吗?
2、若K值发生变化,可能是因为受哪些因素的影响?
思考与讨论
家鼠是一种繁殖力很强的有害动物,仅采取杀死鼠来控制的办法,效果如何?我们应当采取什么措施更好?
既杀死老鼠(数量减少);又清除垃圾,严密储存食物,使环境容纳量降低,即K值降低,这就从根本上限制了老鼠的种群数量
思考:怎样做才是保护大熊猫的根本措施?
建立自然保护区,改善大熊猫的栖息环境,提高环境容纳量(K值)。
思考:在池塘中养鱼,渔民总是希望自己捕的鱼越多越好,但是为了考虑池塘的鱼可持续发展,捕鱼应该选择在种群数量是多少时最好?
K/2
K
超过种群的数量K/2时开始捕鱼
捕到数量下降到K/2时停止
小结:“J”型曲线和“S”型曲线比较
“J”型曲线
“S”型曲线
形成条件
适用范围
增长率(速率)
变化
K
值
理想条件下
资源无限
实验室和种群迁入新的环境中最初的一段时间内的增长
一般自然种群的增长
不变
变化
无
有
K/2
自然条件下
资源有限
环境阻力
“J”型曲线与“S”型曲线的比较
食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等
四、种群数量的波动和下降
大多数种群的数量总是在波动之中的,在不利条件之下,还会急剧下降,甚至灭亡。
五、研究种群数量变化的意义
防治有害动物
蝗虫的防治
野生生物资源的保护和合理利用
鱼类的捕捞
濒危动物种群的拯救和恢复
保护大熊猫
蝗灾
迁飞的蝗群
本节聚焦
一、建构种群增长模型的方法
二、种群增长的“J”型曲线
三、种群增长的“S”型曲线
四、种群数量的波动和下降
五、研究种群数量变化的意义
假设张翰承包了一个鱼塘养鱼虾,如果一次投放的幼苗过多或延迟捕捞,由于环境的负载能力限制,都不能达到效益的最优化;相反,如果大量捕捞,使鱼虾数量大大减少,其种群往往要经过相当长的延滞期才能进入指数增长期,对生产极为不利。那什么时候是捕捞的最佳数量期?
问题:如何合理利用和保护生物资源?
问题:种群的数量变化有怎样的规律?
问题的提出
数学模型:
是用来描述一个系统或它的性质的数学形式。
数学模型的表现形式可以为公式、图表等形式。
一、建构种群增长模型的方法
描述、解释和预测种群数量的变化,常常需要建立数学模型。
一、建构种群增长模型的方法
问题探讨
在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代。
一、建构种群增长模型的方法
时间(min)
20
40
60
80
100
120
140
160
180
分裂次数
数量(个)
2
4
8
16
32
64
128
256
512
1
2
3
4
5
6
7
8
9
1、填写下表:计算一个细菌在不同时间(单位为min)产生后代的数量。
2.n代细菌数量Nn的计算公式是:
Nn
3.72小时后,由一个细菌分裂产生的细菌数量是多少?
=1×2n
解:n=
60min
x72h/20min=216
Nn=1×2n
=2
216
细菌数量
一、建构种群增长模型的方法
4、以时间为横坐标,细菌数量为纵坐标,画出细菌的数量增长曲线。
曲线图与数学方程式比较,有哪些优缺点?
曲线图:
直观,但不够精确。
数学公式:
精确,但不够直观。
一、建构种群增长模型的方法
1、观察研究对象,提出问题
细菌每20分钟分裂一次,
问题:细菌数量怎样变化的?
2、提出合理的假设
在资源和空间无限多的环境中,细菌种群的增长不受种群密度增加的影响
3、根据实验数据,用适当的数学形式对事物的性质进行表达
列出表格,根据表格画曲线,推导公式
4、通过进一步实验或观察等,对模型进行检验或修正
观察、统计细菌的数量,对自己所建立的模型进行检验或修正
建立数学模型一般包括以下步骤:
实例一:1859年,一位英国人来到澳大利亚定居,他带来了24只野兔。让他没有想到的是,一个世纪之后,这24只野兔的后代竟达到6亿只以上。漫山遍野的野兔与牛羊争食牧草,啃啮树皮,造成植被破坏,导致水土流失。后来,人们引入了黏液瘤病毒才使野兔的数量得到控制。
实例二:凤眼莲原产于南美,仅以一种观赏性植物零散分布,1844年在美国的博览会上曾被喻为“美化世界的淡紫色花冠”。自此以后凤眼莲被作为观赏植物引种栽培,现已在亚、非、欧、北美洲等数十个国家造成危害。1901年作为花卉引入中国,30年代作为畜禽饲料引入中国内地各省,并作为观赏和净化水质的植物推广种植,后逃逸为野生。由于繁殖迅速,又几乎没有竞争对手和天敌
,在我国南方江河湖泊中发展迅速,目前我国有这种凤眼莲184万吨,成为我国淡水水体中主要的外来入侵物种之一。
实例三:在20世纪30年代,人们将环颈雉引入美国的一个岛屿。在1937-1942年期间,这个种群数量的增长如下图所示。
如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈什么型?
二、种群增长的“J”型曲线
①产生条件:
理想状态——食物充足,空间不限,
气候适宜,没有天敌等;
②增长特点:
种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
③量的计算:t年后种群的数量为
Nt=N0
λt
(N0为起始数量,
t为时间,Nt表示t年后该种群的数量,λ为年均增长率.)
④例子:实验室条件下、外来物种入侵、
迁移入新环境。
当种群数量呈现增长趋势时,能否通过该数学模型得出种群数量增长率的变化规律?
增长率始终为“λ-1”
λ-1
增长率是指在一段时间内,结束时种群数量相对于初始种群数量的增加部分占初始数量的比例。
问题探讨
在一个培养基中,细菌的数量会一直按照这个公式增长吗?为什么?
如何验证这个观点?
不会。原因是资源和空间是有限的。
生态学家高斯曾经做过这样一个实验:在0.5ml培养液中放入5个大草履虫,然后每隔24h统计一次大草履虫的数量。经过反复实验,得出了如图所示的结果。
思考:
1、曲线形状象什么?其种群达到基本稳定的数量值称为什么?
“S”型曲线
2、大草履虫数量增长过程如何?
三、种群增长的“S”型曲线
K值
种群增长速率不断降低
种群数量K/2
→K值时,
三、种群增长的“S”型曲线
种群数量达到K值时,
种群增长速率为零,但种群数量达到最大,且种内斗争最剧烈。
种群数量在
K/2值时,
种群增长速率最大
种群数量由0→K/2值时,
种群增长率速增大
K值:在环境条件不受破坏的情况下,一定空间中所能维持的种群最大数量称为环境容纳量。
K/2
转折期,增长速率最快
K值:环境容纳量
加速期,个体数量增加,增长加速
潜伏期,个体数量较少增长缓慢
减速期,增长缓慢
饱和期,增长速率为零
种
群
数
量
“S”
型
增
长
曲
线
(种群数量)
K/2
K
种
群
数
量
增
长
速率
时间
D:
种群数量处于K值,
增长率为0
B:
种群数量处于K/2值,
种群增长率最大
增长速率随时间变化曲线
B
D
讨论:
1、同一种群的K值是固定不变的吗?
2、若K值发生变化,可能是因为受哪些因素的影响?
思考与讨论
家鼠是一种繁殖力很强的有害动物,仅采取杀死鼠来控制的办法,效果如何?我们应当采取什么措施更好?
既杀死老鼠(数量减少);又清除垃圾,严密储存食物,使环境容纳量降低,即K值降低,这就从根本上限制了老鼠的种群数量
思考:怎样做才是保护大熊猫的根本措施?
建立自然保护区,改善大熊猫的栖息环境,提高环境容纳量(K值)。
思考:在池塘中养鱼,渔民总是希望自己捕的鱼越多越好,但是为了考虑池塘的鱼可持续发展,捕鱼应该选择在种群数量是多少时最好?
K/2
K
超过种群的数量K/2时开始捕鱼
捕到数量下降到K/2时停止
小结:“J”型曲线和“S”型曲线比较
“J”型曲线
“S”型曲线
形成条件
适用范围
增长率(速率)
变化
K
值
理想条件下
资源无限
实验室和种群迁入新的环境中最初的一段时间内的增长
一般自然种群的增长
不变
变化
无
有
K/2
自然条件下
资源有限
环境阻力
“J”型曲线与“S”型曲线的比较
食物不足
空间有限
种内斗争
天敌捕食
气候不适
寄生虫
传染病等
四、种群数量的波动和下降
大多数种群的数量总是在波动之中的,在不利条件之下,还会急剧下降,甚至灭亡。
五、研究种群数量变化的意义
防治有害动物
蝗虫的防治
野生生物资源的保护和合理利用
鱼类的捕捞
濒危动物种群的拯救和恢复
保护大熊猫
蝗灾
迁飞的蝗群
同课章节目录
- 第1章 人体的内环境与稳态
- 第1节 细胞生活的环境
- 第2节 内环境稳态的重要性
- 第2章 动物和人体生命活动的调节
- 第1节 通过神经系统的调节
- 第2节 通过激素的调节
- 第3节 神经调节与体液调节的关系
- 第4节 免疫调节
- 第3章 植物的激素调节
- 第1节 植物生长素的发现
- 第2节 生长素的生理作用
- 第3节 其他植物激素
- 第4章 种群和群落
- 第1节 种群的特征
- 第2节 种群数量的变化
- 第3节 群落的结构
- 第4节 群落的演替
- 第5章 生态系统及其稳定性
- 第1节 生态系统的结构
- 第2节 生态系统的能量流动
- 第3节 生态系统的物质循环
- 第4节 生态系统的信息传递
- 第5节 生态系统的稳定性
- 第6章 生态环境的保护
- 第1节 人口增长对生态环境的影响
- 第2节 保护我们共同的家园
