3.3 立方根

(共20张PPT)
一、复习
(1) 什么叫一个数a的平方根 如何用符号表示数a(≥0)的 平方根
(2) 正数有几个平方根 它们之间的关系是什么 负数有没有平方根 0平方根是什么
(3) 当a≥0时，式子 ,－ ，± ，的意义各是什么
1.口答：
2.计算：
±
这是由几个大小相同的单位立方体组成的魔方
合作学习
3.3 立方根
情境引入

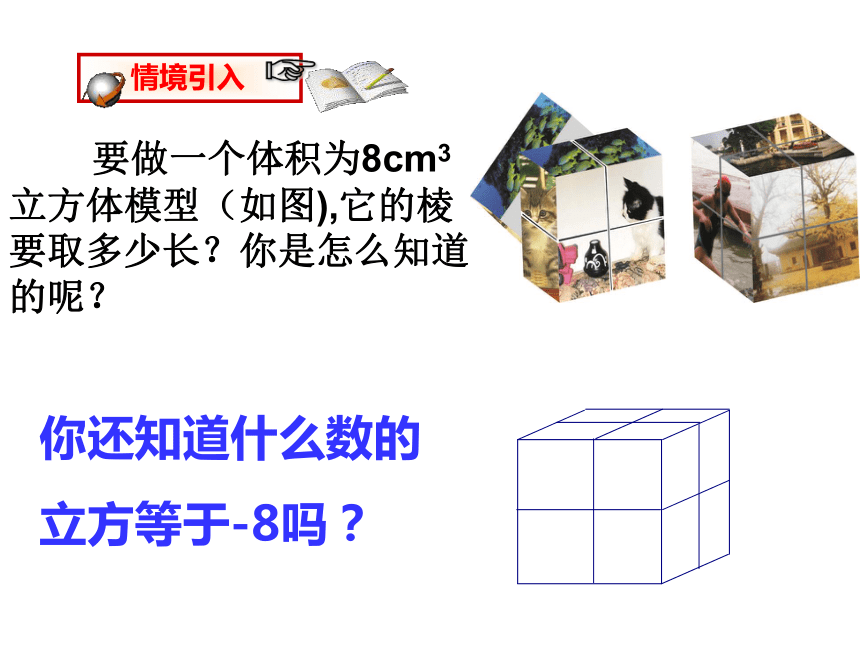
要做一个体积为8cm3立方体模型（如图),它的棱要取多少长？你是怎么知道的呢？
你还知道什么数的
立方等于-8吗？
看一看
平方根的概念：
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，也叫做a的二次方根。
例如，因为32=9，所以3是9的平方根；又因为（-3）2=9，所以-3也是9的平方根。（9的平方根为+3和-3）
你能用上面的阅读材料仿造立方根的概念吗？你还知道8的立方根吗？（尝试一下，你行的）
-8的立方根呢？
1 -1 -0.008呢？
正数的平方根用“± ”表示（读作“正负根号a”)
算术平方根用 表示（读作“根号a”）
找一找

那么你知道立方根怎么表示吗？找一找，你会得到结果的。
温馨提醒：
中的根指数3不能省略，要写在根号的左上角。
例题欣赏
求下列各数的立方根：
（1）27
解：∵33=27，
∴27的立方根是3，即 =3.
（2）
（3）-64 （4） －27
（5）-0.008 （6） 0
同学们，你们能独立完成上面的题目吗？
试一试！
(4)－27
因为(-3)3=-27，所以-27的立方根是-3，即
思考：
除－3以外，还有什么数的立方等于-27 ， 也就是说，负数－27还有别的立方根吗
(6)0
因为03=0，所以0的立方根是0，即 =0.
　　
通过对以上问题的解答，你能总结出立方根有什么样的性质？
正数有一个正的立方根；负数有一个负的立方根；零的立方根仍旧是零.
　
说明：立方根的个数的性质可以概括为立方根的唯一性，即一个数的立方根是唯一的.
一般地，一个数x的立方等于a，即
那么这个数x就叫做a的立方根（也叫做a的三次方根），记做
。如：
，则2叫做8的立方根，即
，则
是
的立方根，即
其中a是被开方数，3是根指数，符号
读做“三次根号”。
根据前面的练习结果，你能得到立方根和平方根的相同与不同吗？
合作交流

相同：
不同：
零的平方根和立方根都是零。
正数有一正一负两个平方根，而正数只有一个正立方根。
负数没有平方根，而负数有一个负的立方根。
判断下列说法是否正确，并说明理由
（1）4的平方根是2 ( )
（2） 的立方根是± ( )
（3）负数不能开立方 ( )
（4）-8的立方根是-2 ( )
（5） 立方根是它本自身的只有零。 ( )
探索思考
×
√
×
×
×
计算：
（1）
（2）
（3） +
（4） +
试一试
（1） 的立方根是_______.
（2） 是_____的立方根.
（3）81的平方根的立方根是_______.
（4） _______.
（5） 的立方根是______.
（6） 的立方根是________.
（7）若 ，则 _______.
小结：比一比
1、平方根的定义：如果一个数的平方等于a,那么这个数叫做a的平方根。a的平方根用±
2、平方根的性质
（1）一个正数有两个平方 根，这两个平方根互为相反数
（2）0的平方根还是0（3）负数没有平方根
1、立方根的定义：如果一个数的立方等于a,那么这个数叫做a的立方根。a的立方根用 表示
2、立方根的性质
（1）正数的立方根还是正数
（2）0的立方根还是0
（3）负数的立方根还是负数
一般地，如果一个数的立方等于a，那么这个数叫做a的立方根，也叫做a的三次方根。记作 读作“三次根号a”，其中a是被开方数，3是根指数。
一个正数有一个正的立方根；一个负数有一个负的立方根； 零的立方根是零。
立方根
立方根与平方根比较
一个正数有一正一负两个平方根；负数没有平方根； 零的平方根是零。
－8
规律：对于任何数a都有
求下列各数的值，并找规律。
2
-2
-3
4
规律：对于任何数a都有
0
8
27
-27
0
5
一个正方体的体积是216cm3,现将它锯成8块大小一样的正方体小木块，那么你知道每一个小正方体的表面积是多少吗？
作业：
作业本(2)：3.3立方根
思考：
是由平方根的性质所得。
那么，对于
？