浙教版八年级数学上册课件:1.5三角形全等的判定(18张)
文档属性
| 名称 | 浙教版八年级数学上册课件:1.5三角形全等的判定(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 16:05:11 | ||
图片预览


文档简介
(共18张PPT)
1.5
三角形全等的判定(2)
回顾与思考
到目前为止,我们已学过哪些方法判定两三角形全等?
2.边边边公理(SSS)
1.
全等三角形的定义
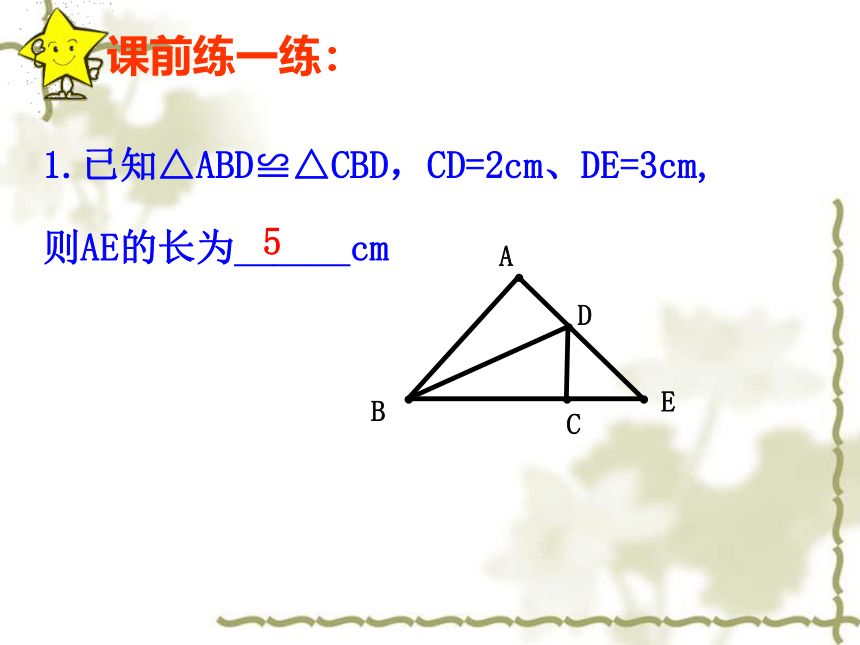
1.已知△ABD≌△CBD,CD=2cm、DE=3cm,
则AE的长为______cm
课前练一练:
5
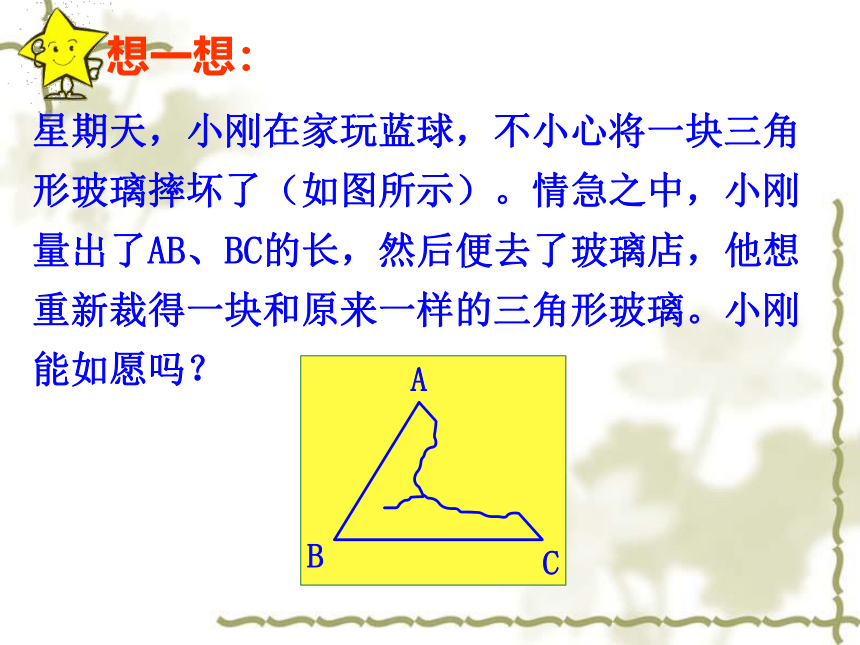
想一想:
星期天,小刚在家玩蓝球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?
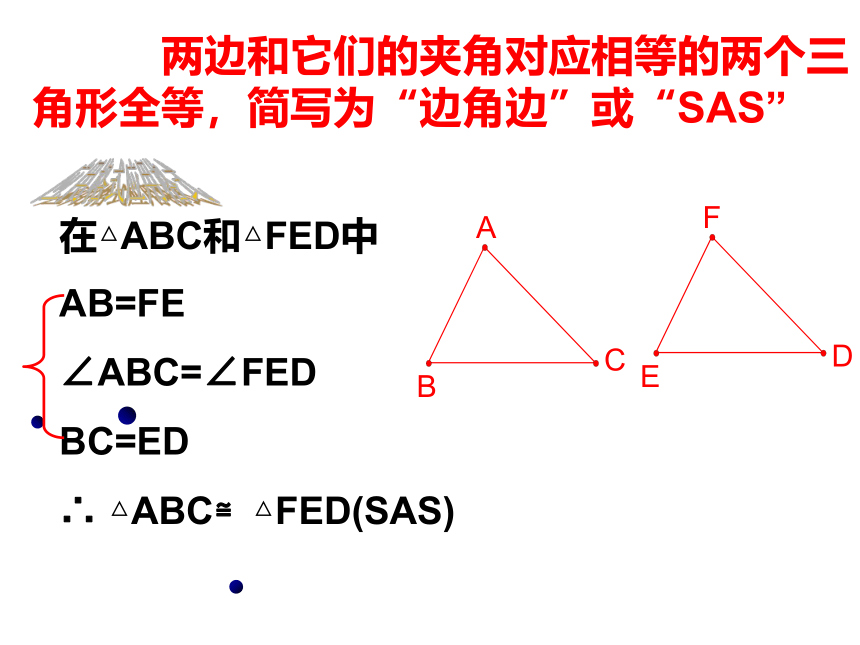
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”
应用格式
在△ABC和△FED中
AB=FE
∠ABC=∠FED
BC=ED
∴
△ABC≌△FED(SAS)
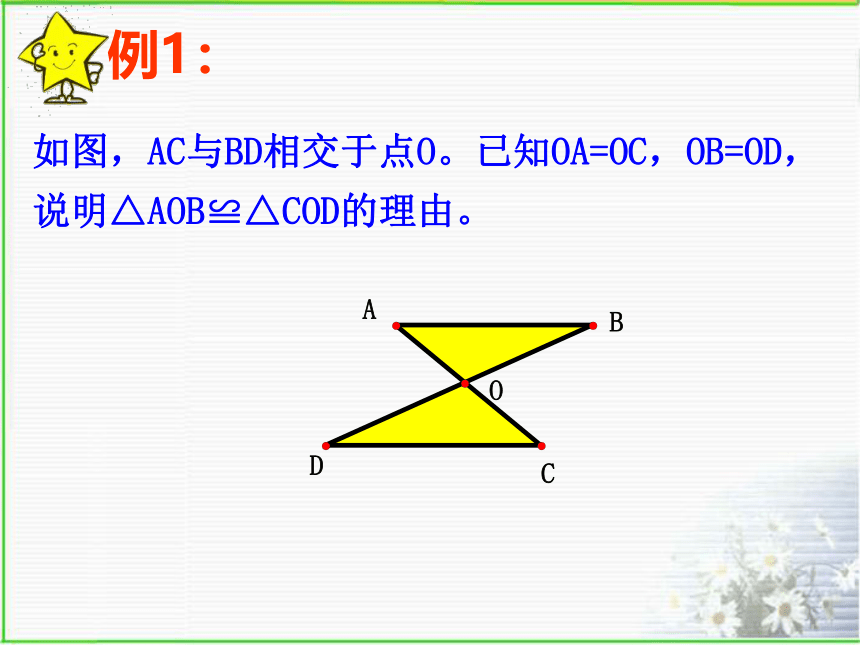
例1:
如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
想一想:
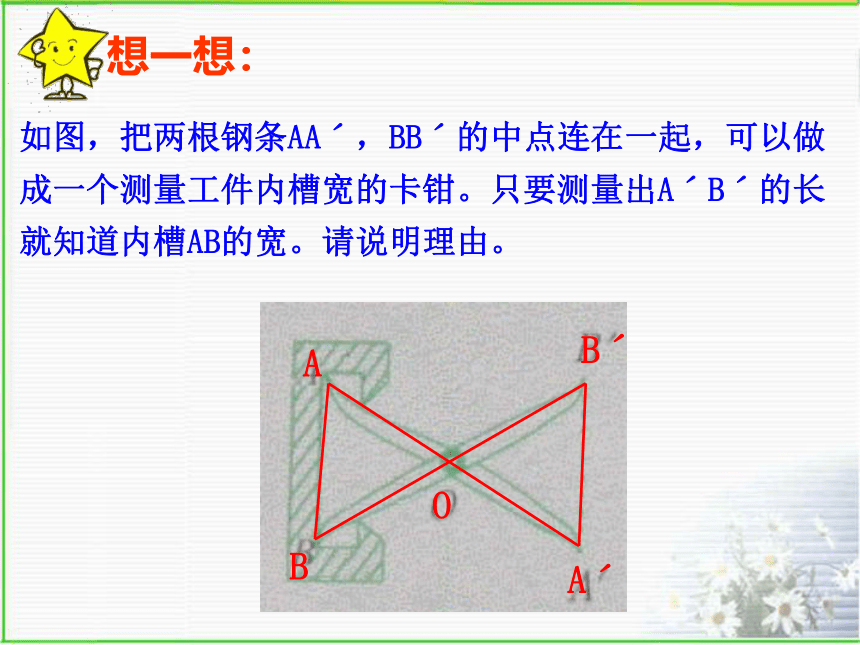
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。
A
B
Aˊ
Bˊ
O
小明做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
E
F
D
H
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
解:已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB(
SAS)
∴CA=CB(全等三角形对应边相等)
例2
如图,直线
⊥AB,垂足为O且OA=OB,点C是直线
上任意一点,说明CA=CB的理由。
∵直线
⊥AB
中垂线的性质
线段垂直平分线上的点到线段两端点的距离相等
垂直平分线定义
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线
∵l(CO)是AB的中垂线
∴AC=BC(中垂线的性质)
A
C
O
B
l
补充练习:
①.
如图(1),
△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
②
如图(2),
△ABC中,DE垂直平分AC,AE=2.5cm,
△ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
探索
1.通过例4你能发现线段AB和直线DE之间有什么特殊的位置关系?
结论:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
2.如图直线a垂直平分线段AB.则CA与CB,DA与DB,EA与EB之间有什么关系?由此你能得出什么结论?
A
B
C
D
E
a
结论:线段垂直平分线上的点到线段两端点的距离相等.
关系:CA=CB,
DA=DB,
EA=EB.
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40o,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
试一试:
1、今天我们学习哪种方法判定两三角形全等?
答:边角边(SAS)
2、通过这节课,判定三角形全等的条件有哪些?
答:全等三角形的定义 SSS、SAS
3.“边边角”能不能判定两个三角形全等?
小结
F
E
D
C
B
A
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
解:全等。∵BD=EC(已知)
∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE(SAS)
∴AB=DE
E
C
B
A
D
如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。
解:在△ACB和△DCE中
再
见
祝同学们学习进步
1.5
三角形全等的判定(2)
回顾与思考
到目前为止,我们已学过哪些方法判定两三角形全等?
2.边边边公理(SSS)
1.
全等三角形的定义
1.已知△ABD≌△CBD,CD=2cm、DE=3cm,
则AE的长为______cm
课前练一练:
5
想一想:
星期天,小刚在家玩蓝球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”
应用格式
在△ABC和△FED中
AB=FE
∠ABC=∠FED
BC=ED
∴
△ABC≌△FED(SAS)
例1:
如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
想一想:
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。
A
B
Aˊ
Bˊ
O
小明做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
E
F
D
H
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
解:已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB(
SAS)
∴CA=CB(全等三角形对应边相等)
例2
如图,直线
⊥AB,垂足为O且OA=OB,点C是直线
上任意一点,说明CA=CB的理由。
∵直线
⊥AB
中垂线的性质
线段垂直平分线上的点到线段两端点的距离相等
垂直平分线定义
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线
∵l(CO)是AB的中垂线
∴AC=BC(中垂线的性质)
A
C
O
B
l
补充练习:
①.
如图(1),
△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
②
如图(2),
△ABC中,DE垂直平分AC,AE=2.5cm,
△ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
探索
1.通过例4你能发现线段AB和直线DE之间有什么特殊的位置关系?
结论:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
2.如图直线a垂直平分线段AB.则CA与CB,DA与DB,EA与EB之间有什么关系?由此你能得出什么结论?
A
B
C
D
E
a
结论:线段垂直平分线上的点到线段两端点的距离相等.
关系:CA=CB,
DA=DB,
EA=EB.
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40o,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
试一试:
1、今天我们学习哪种方法判定两三角形全等?
答:边角边(SAS)
2、通过这节课,判定三角形全等的条件有哪些?
答:全等三角形的定义 SSS、SAS
3.“边边角”能不能判定两个三角形全等?
小结
F
E
D
C
B
A
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
解:全等。∵BD=EC(已知)
∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE(SAS)
∴AB=DE
E
C
B
A
D
如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。
解:在△ACB和△DCE中
再
见
祝同学们学习进步
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
