浙教版八年级数学上册课件:第一章《三角形的初步知识》复习(共48张PPT)
文档属性
| 名称 | 浙教版八年级数学上册课件:第一章《三角形的初步知识》复习(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-07 16:10:41 | ||
图片预览




文档简介
(共48张PPT)
三角形的初步知识
--复习课
三角形的性质
(1)边上的性质:
三角形的两边之和大于第三边
三角形的两边之差小于第三边
(2)角上的性质:
三角形三内角和等于180度
三角形的一个外角等于和它不相邻的两个内角之和
辨一辨:
1、下列每组分别是三根小木棒的长度,用它们能摆成三角形吗?(单位:厘米。填“能”或“不能”)
(1)3,4,5(
)
(2)8,7,15(
)
(3)13,12,20(
)
(4)5,5,11(
)
不能
不能
能
能
直角三角形
钝角三角形
2、三角形按内角的大小分为三类:①锐角三角形;
②直角三角形;③钝角三角形。根据下列条件判断它们
是什么三角形?
(1)三个内角的度数是1:2:3(
)
(2)两个内角是50°和30°(
)
c
3、三角形的两边长分别是3和5,第三边a的取值范围(
)
A、2≤a<8
B、2<a≤8
C、2<a<8
D、2≤a≤8
4、以下各组线段,能组成三角形的是( )
A.2cm,2cm,4cm
B.3cm,6cm,8cm
C.2cm,3cm,6cm
D.4cm,6cm,11cm
B
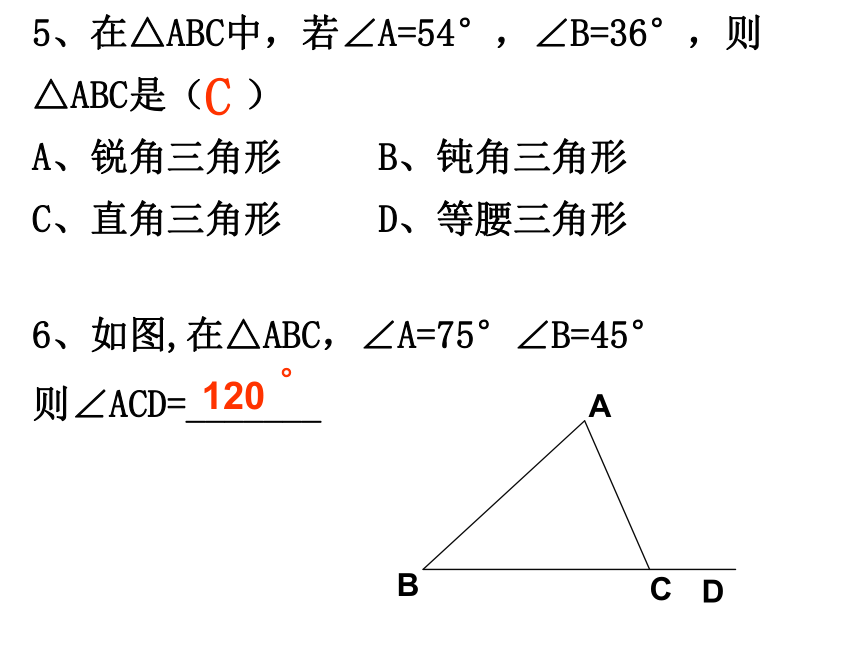
5、在△ABC中,若∠A=54°,∠B=36°,则△ABC是(
)
A、锐角三角形
B、钝角三角形
C、直角三角形
D、等腰三角形
C
6、如图,在△ABC,∠A=75°∠B=45°
则∠ACD=_______
120
。
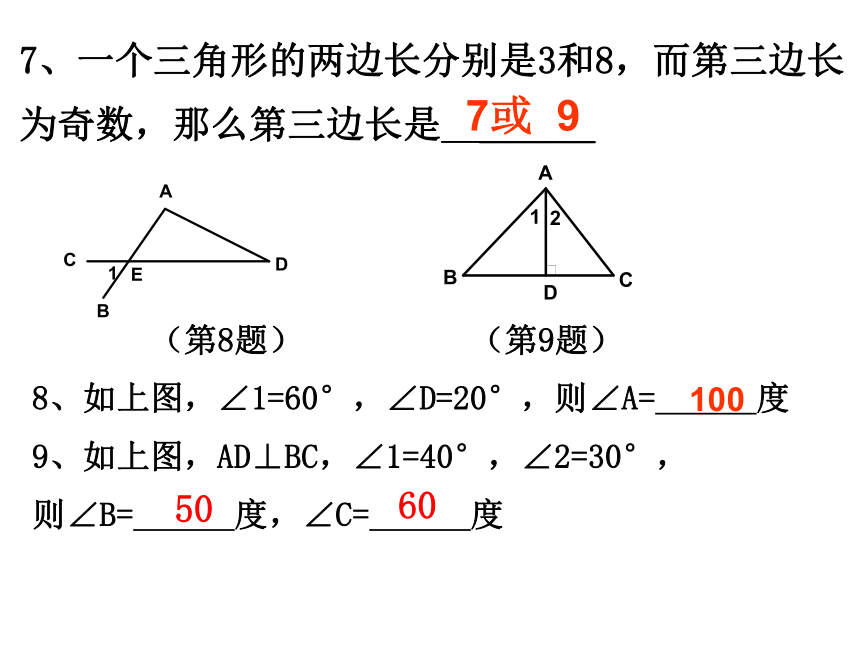
(第8题)
(第9题)
8、如上图,∠1=60°,∠D=20°,则∠A=
度
9、如上图,AD⊥BC,∠1=40°,∠2=30°,
则∠B=
度,∠C=
度
7或
9
100
50
60
7、一个三角形的两边长分别是3和8,而第三边长为奇数,那么第三边长是
______
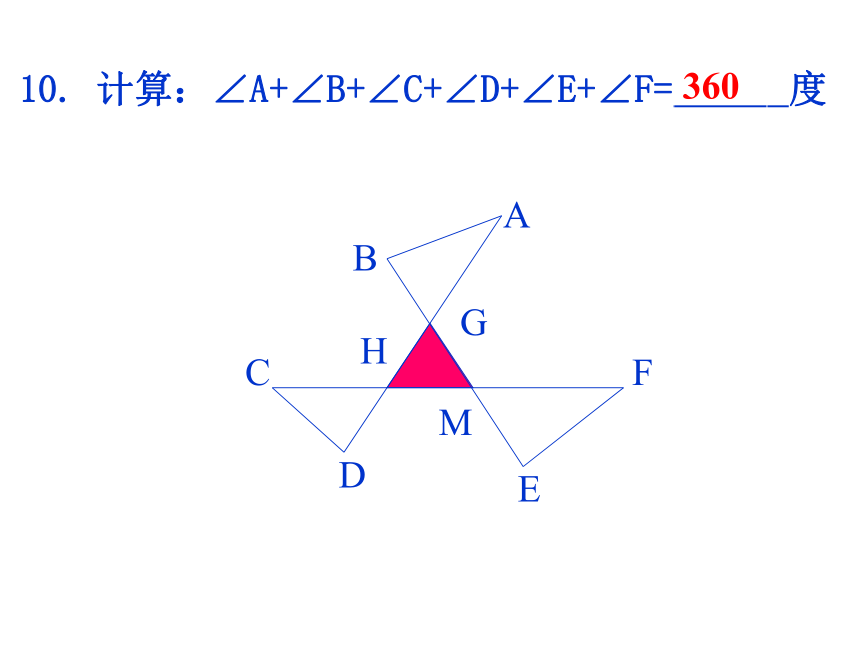
10.
计算:∠A+∠B+∠C+∠D+∠E+∠F=
度
B
C
D
A
G
M
H
E
F
360
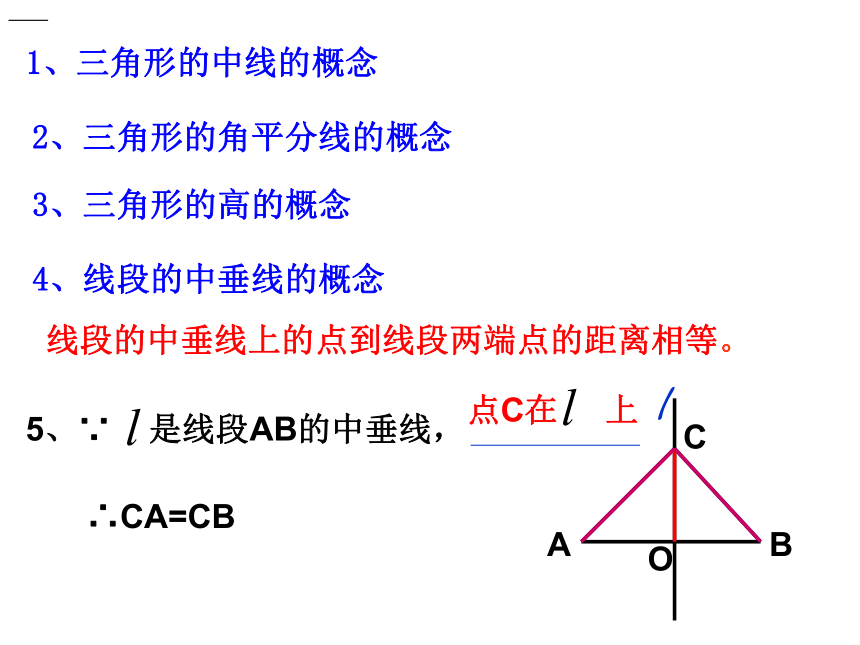
A
C
O
B
l
∴CA=CB
点C在
上
5、∵
是线段AB的中垂线,
线段的中垂线上的点到线段两端点的距离相等。
1、三角形的中线的概念
2、三角形的角平分线的概念
3、三角形的高的概念
4、线段的中垂线的概念
A
B
C
P
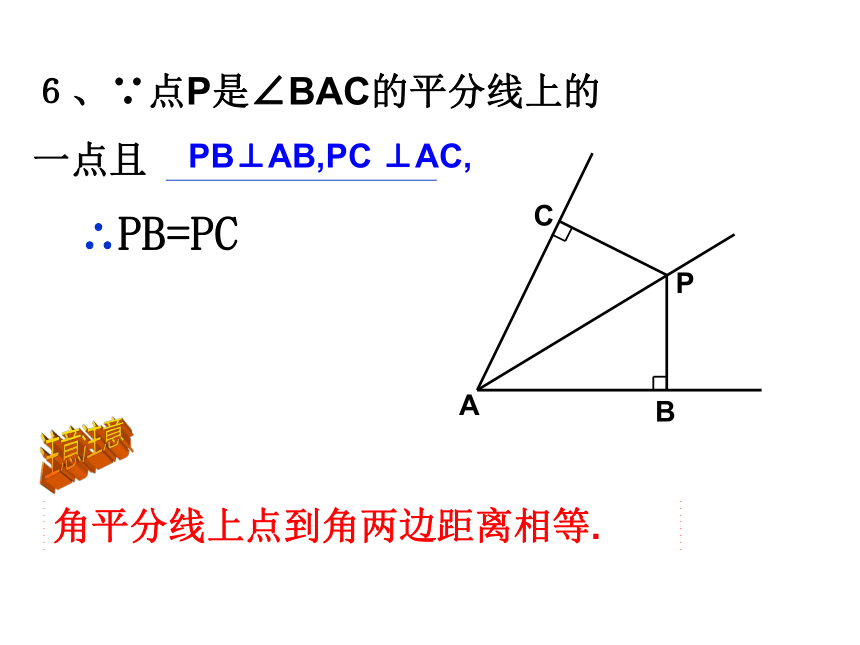
∴PB=PC
PB⊥AB,PC
⊥AC,
6、∵点P是∠BAC的平分线上的
一点且
角平分线上点到角两边距离相等.
注意
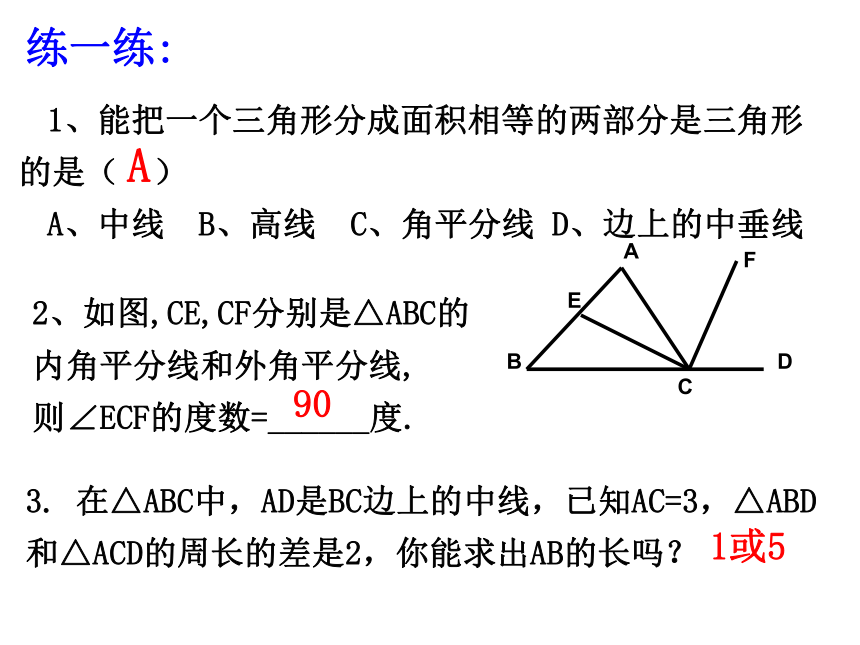
2、如图,CE,CF分别是△ABC的内角平分线和外角平分线,
则∠ECF的度数=______度.
B
C
D
F
E
A
3.
在△ABC中,AD是BC边上的中线,已知AC=3,△ABD和△ACD的周长的差是2,你能求出AB的长吗?
练一练:
90
1或5
1、能把一个三角形分成面积相等的两部分是三角形
的是(
)
A、中线
B、高线
C、角平分线
D、边上的中垂线
A
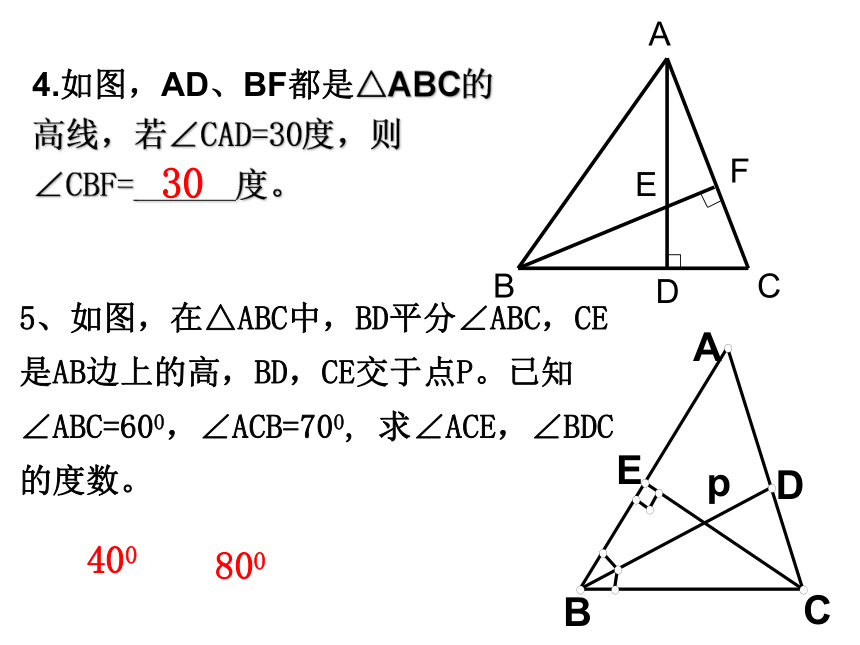
5、如图,在△ABC中,BD平分∠ABC,CE是AB边上的高,BD,CE交于点P。已知∠ABC=600,∠ACB=700,
求∠ACE,∠BDC的度数。
400
800
A
B
C
E
D
F
4.如图,AD、BF都是△ABC的高线,若∠CAD=30度,则∠CBF=______度。
30
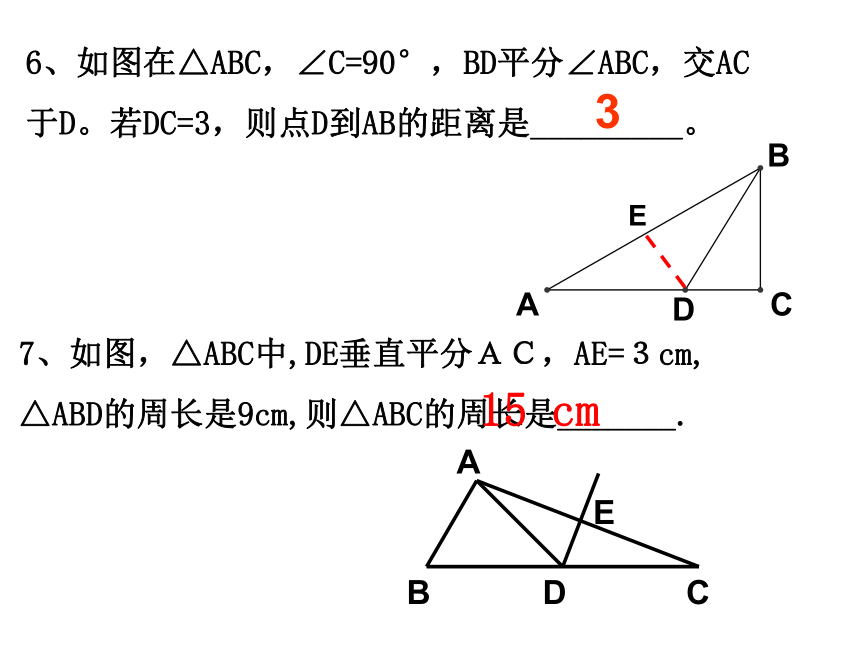
6、如图在△ABC,∠C=90°,BD平分∠ABC,交AC
于D。若DC=3,则点D到AB的距离是_________。
E
3
7、如图,△ABC中,DE垂直平分AC,AE=3cm,
△ABD的周长是9cm,则△ABC的周长是_______.
A
B
C
D
E
15
cm
8、如图,已知△ABC中,∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,则∠DAE=
;
150
9、如图,BE、CF是△ABC
的角平分线,∠A=40°求∠BOC度数.
1100
改变条件:
1、如图,BE、CF是△ABC
的外角平分线,
∠A=40°求∠BOC度数.
700
2、如图,BE、CF分别是△ABC
的内角与外角平分线,∠A=40°求∠BOC度数.
200
全等图形:
全等三角形:
基础知识
能够完全重合的两个图形
能够完全重合的两个三角形
三角形全等的判定方法
(1)边边边公理(SSS)
(2)边角边公理(SAS)
三边对应相等的两个三角形全等
两边及它们的夹角对应相等的两个三角形全等
(3)角边角公理(ASA)
两角及它们的夹边对应相等的两个三角形全等
(4)角角边公理(AAS)
两角及其中一角的对边对应相等的两个三角形全等
全等三角形的对应边相等;
全等三角形的对应角相等;
全等三角形的对应线段相等;
全等三角形的面积相等。
全等三角形的性质:
平移类
旋转类
翻转类
综合类
如图,∠1=∠2,∠3=∠4请说明AB=CD理由
解:在
中
∴
△
≌△
(
)
∴AB=CD(
)
△ABC和△CDA
∠1=∠2,
∠3=∠4
AC=CA
ACB
CAD
ASA
全等三角形的对应边相等
(已知)
(已知)
(公共边)
A
B
C
D
1
2
3
4
全等的格式
3、判断题:
(1)有两边和其中一边的对角对应相等的两个三角形全等.(
)
(2)有三角对应相等的两个三角形全等。
(
)
(3)成轴对称的两个三角形全等。(
)
(4)面积相等的两个三角形全等。
(
)
(5)含有60°角的两个直角三角形全等。
(
)
4、如图,已知AC平分∠BCD,要说明△ABC≌△ADC,还需要增加一个什么条件?请说明理由。
D
C
A
B
或∠BAC=∠DAC
BC=CD
或∠B=∠D
5、如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
(1)图中有哪些全等的三角形?
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
(2)图中有哪些相等的线段?
(3)图中有哪些相等的角?
6、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有(
)
A.1对
B.2对
C.3对
D.4对
D
O
D
B
E
C
A
1
2
阅读下题及其说理过程:
已知:如图,D是⊿ABC中BC边上的中点,EB=EC,∠ABE=∠ACE,说明∠BAE=∠CAE的理由。
解:在AEB和AEC中
EB=EC
∠ABE=∠ACE
AE=AE
∴⊿AEB≌∠AEC
∴∠BAE=∠CAE
A
B
C
D
E
问:上面说理过程是否正确?若正确,请写出每一步的推理根据;若不正确,请指出错在哪一步,并写出你认为正确的推理过程.
例1、已知如图,AB=AC,AO平分∠BAC,请说明(1)△ABO≌△ACO;(2)DO=EO的理由.
A
B
C
O
D
E
1
2
3
4
解(1)∵
AO平分∠BAC
∴∠1=∠2
(已知)
(角平分线定义)
在△ABO和△ACO中
AB=AC
AO=AO
(已知)
(公共边)
∴
△ABO≌△ACO
(SAS)
(2)∵△ABO≌△ACO
∴
∠B=∠C
OB=0C
(全等三角形的对应角、对应边相等)
∠1=∠2
在△BOD和△COE中
∠3=
∠4
OB=0C
∠B=∠C
(对顶角相等)
∴
△BOD≌△COE
(ASA)
∴DO=EO
(全等三角形的对应边相等)
例2、如图,AD是△ABC的高,且AD平分∠BAC,
请指出∠B与∠C的关系,并说明理由。
A
B
C
D
解:∵AD是△ABC的高
∴∠ADB=∠ADC=90°
∵AD平分∠BAC
∴∠BAD=∠CAD
在△ABD和△ACD中,
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
∴
△ABD≌
△ACD
∴∠B=∠C
八上
1.53课后
No.10
证明:∵AD是△ABC的高,
∴∠ADC=
90°∴∠DAC+∠C
=
90°
同理∠EBC+∠C
=
90°,
∴∠DAC=∠EBC.
∵AD=BD,∠BDH=∠ADC
=
90°,
∴ΔBDH≌ΔADC.
八上
1.54提高
No.11
(1)提示:证明△ABD≌△CAE,
∴AD=CE,BD=AE,
∴BD=AE=AD+DE=CE+DE;
八上
1.54提高
No.12
(2)BD=DE-CE,
提示:证明△ABD≌△CAE
C
B
D
E
ΔCBD≌ΔABE
A
CB
=
AB
S
S
BD=BE
A
∠CBD
=
∠ABE
∠EBD
-∠EBC
=
∠ABC
-∠EBC
∠EBD
=
∠ABC
=
60°
例3、如图,已知:ΔABC和ΔBDE是等边三角形,D在AE的延长线上。求证:ΔCBD≌ΔABE
A
B
C
D
E
变式1、如图,已知:ΔABC和ΔBDE是等边三角形,D在AE的延
长线上。
求证:BD
+
DC
=
AD
A
C
D
E
B
ΔCBD
≌
ΔABE
∠CBA+
∠DBA
=
∠EBD+
∠DBA
∠CBA=
∠EBD=
60°
CB=
AB
DB
=
EB
∠CBD=
∠ABE
变式2、如图,已知:点C、B、E在同一条直线上,ΔABC和ΔBDE是等边三角形。
求证:
ΔCBD≌ΔABE
A
C
D
E
B
G
H
变式3、
如图,已知△ABC和△DEB等边三角形
。C,B,E在一条直线上
求证:
BG
=
BH。
八上
1.6课后
No.9
连结AB,BC,
分别作线段AB,BC的垂直平分线,
交点的位置就是学校的位置
例4、如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB,②AE=CF,③∠B=∠D,④
∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
A
B
C
D
E
F
B
A
F
C
D
E
1、如图,已知AB=ED,AF=CD,EF=BC,
说明∠EFD=∠BCA的理由。
2、如图,∠1=∠2,AB=CD,AC与BD相交于点O,则图中必定全等的三角形有(
)
A.
2对
B.
3对
C.
4对
D.
6对
A
O
D
C
B
1
2
C
巩固练习:
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,则∠B=∠C,请说明理由.
(提示:连结AD)
4.如图,在△ABC中,
AD是△BAC的角平分线,DE是△ABD的高线,
∠C=90
度。若DE=2,BD=3,求线段BC的长。
B
D
E
A
C
5、如下图,已知△ABC中,DE是BC边上的中垂线,若AC=5,EC=2,
△ADC的周长是13,求△ABC的周长。
A
B
C
D
E
6、如上图,EF是AB的中垂线,分别延长BE、AE至D,C,使DE=CE,则AD与BC相等吗?
请说明理由。
A
B
C
D
E
F
A
B
C
D
E
7、如下图,已知AD是△ABC的中线,CE是△ADC的中线,若△ABC的面积是8,求△DEC的面积。
8、如上图,△ABC中,点D是BC上的一点,点E是AD上的一点,若BD:CD=2:3,DE:AE=1:4,△ABC的面积是8,求△DEC的面积。
A
B
C
D
E
要想知道一个池塘的两岸上最远两点之间的距离,没有船,且不能直接去测量。如果只用绳子和尺子,怎样才能测出它们之间的距离呢?
它们之间有多远呢?
方案设计
A
B
A
B
C
E
D
ABC≌ DEC(SAS)
AB = DE
在
ABC与
DEC中,
AC = DC
∠ACB=∠DCE
BC = EC
先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离。
方案一
△
ACD≌
△
CAB(SAS)
AB
=
CD
方
案
二
B
C
A
D
1
2
∠1=∠2
AD=CB
AC=CA
解:连结AC,由AD∥CB,可得∠1=∠2
在△ACD与△CAB中
如图,先作三角形ABC,再找一点D,使AD∥BC,并使AD=BC,连结CD,量CD的长即得AB的长
方案三
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长。
B
A
D
C
解:
在Rt ADB与Rt CDB中
ADB≌ CDB(SAS)
∴
BA
=
BC
BD=BD
∠ADB=∠CDB
CD=AD
1、已知钝角△ABC,求作:
(1)AC边上的中线;
(2)∠C的角平分线;
(3)
BC边上的高。
A
B
C
作图类:
2、已知线段a、b、c,作△ABC,使AB=c,AC=b,BC=a。
a
c
b
3、已知线段a、b、∠α,作△ABC,使AB=a,AC=b,∠A=
∠α
。
a
b
α
4、已知线段a、∠α
∠β
、,作△ABC,使AB=a,∠A=
∠α,
∠A=
∠
β
。
a
α
β
回顾、反思
三角形的初步知识
--复习课
三角形的性质
(1)边上的性质:
三角形的两边之和大于第三边
三角形的两边之差小于第三边
(2)角上的性质:
三角形三内角和等于180度
三角形的一个外角等于和它不相邻的两个内角之和
辨一辨:
1、下列每组分别是三根小木棒的长度,用它们能摆成三角形吗?(单位:厘米。填“能”或“不能”)
(1)3,4,5(
)
(2)8,7,15(
)
(3)13,12,20(
)
(4)5,5,11(
)
不能
不能
能
能
直角三角形
钝角三角形
2、三角形按内角的大小分为三类:①锐角三角形;
②直角三角形;③钝角三角形。根据下列条件判断它们
是什么三角形?
(1)三个内角的度数是1:2:3(
)
(2)两个内角是50°和30°(
)
c
3、三角形的两边长分别是3和5,第三边a的取值范围(
)
A、2≤a<8
B、2<a≤8
C、2<a<8
D、2≤a≤8
4、以下各组线段,能组成三角形的是( )
A.2cm,2cm,4cm
B.3cm,6cm,8cm
C.2cm,3cm,6cm
D.4cm,6cm,11cm
B
5、在△ABC中,若∠A=54°,∠B=36°,则△ABC是(
)
A、锐角三角形
B、钝角三角形
C、直角三角形
D、等腰三角形
C
6、如图,在△ABC,∠A=75°∠B=45°
则∠ACD=_______
120
。
(第8题)
(第9题)
8、如上图,∠1=60°,∠D=20°,则∠A=
度
9、如上图,AD⊥BC,∠1=40°,∠2=30°,
则∠B=
度,∠C=
度
7或
9
100
50
60
7、一个三角形的两边长分别是3和8,而第三边长为奇数,那么第三边长是
______
10.
计算:∠A+∠B+∠C+∠D+∠E+∠F=
度
B
C
D
A
G
M
H
E
F
360
A
C
O
B
l
∴CA=CB
点C在
上
5、∵
是线段AB的中垂线,
线段的中垂线上的点到线段两端点的距离相等。
1、三角形的中线的概念
2、三角形的角平分线的概念
3、三角形的高的概念
4、线段的中垂线的概念
A
B
C
P
∴PB=PC
PB⊥AB,PC
⊥AC,
6、∵点P是∠BAC的平分线上的
一点且
角平分线上点到角两边距离相等.
注意
2、如图,CE,CF分别是△ABC的内角平分线和外角平分线,
则∠ECF的度数=______度.
B
C
D
F
E
A
3.
在△ABC中,AD是BC边上的中线,已知AC=3,△ABD和△ACD的周长的差是2,你能求出AB的长吗?
练一练:
90
1或5
1、能把一个三角形分成面积相等的两部分是三角形
的是(
)
A、中线
B、高线
C、角平分线
D、边上的中垂线
A
5、如图,在△ABC中,BD平分∠ABC,CE是AB边上的高,BD,CE交于点P。已知∠ABC=600,∠ACB=700,
求∠ACE,∠BDC的度数。
400
800
A
B
C
E
D
F
4.如图,AD、BF都是△ABC的高线,若∠CAD=30度,则∠CBF=______度。
30
6、如图在△ABC,∠C=90°,BD平分∠ABC,交AC
于D。若DC=3,则点D到AB的距离是_________。
E
3
7、如图,△ABC中,DE垂直平分AC,AE=3cm,
△ABD的周长是9cm,则△ABC的周长是_______.
A
B
C
D
E
15
cm
8、如图,已知△ABC中,∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,则∠DAE=
;
150
9、如图,BE、CF是△ABC
的角平分线,∠A=40°求∠BOC度数.
1100
改变条件:
1、如图,BE、CF是△ABC
的外角平分线,
∠A=40°求∠BOC度数.
700
2、如图,BE、CF分别是△ABC
的内角与外角平分线,∠A=40°求∠BOC度数.
200
全等图形:
全等三角形:
基础知识
能够完全重合的两个图形
能够完全重合的两个三角形
三角形全等的判定方法
(1)边边边公理(SSS)
(2)边角边公理(SAS)
三边对应相等的两个三角形全等
两边及它们的夹角对应相等的两个三角形全等
(3)角边角公理(ASA)
两角及它们的夹边对应相等的两个三角形全等
(4)角角边公理(AAS)
两角及其中一角的对边对应相等的两个三角形全等
全等三角形的对应边相等;
全等三角形的对应角相等;
全等三角形的对应线段相等;
全等三角形的面积相等。
全等三角形的性质:
平移类
旋转类
翻转类
综合类
如图,∠1=∠2,∠3=∠4请说明AB=CD理由
解:在
中
∴
△
≌△
(
)
∴AB=CD(
)
△ABC和△CDA
∠1=∠2,
∠3=∠4
AC=CA
ACB
CAD
ASA
全等三角形的对应边相等
(已知)
(已知)
(公共边)
A
B
C
D
1
2
3
4
全等的格式
3、判断题:
(1)有两边和其中一边的对角对应相等的两个三角形全等.(
)
(2)有三角对应相等的两个三角形全等。
(
)
(3)成轴对称的两个三角形全等。(
)
(4)面积相等的两个三角形全等。
(
)
(5)含有60°角的两个直角三角形全等。
(
)
4、如图,已知AC平分∠BCD,要说明△ABC≌△ADC,还需要增加一个什么条件?请说明理由。
D
C
A
B
或∠BAC=∠DAC
BC=CD
或∠B=∠D
5、如图,在△ABC中,AB=AC,E、F分别为AB、AC上的点,且AE=AF,BF与CE相交于点O。
A
O
F
E
B
C
(1)图中有哪些全等的三角形?
△EBC≌△FCB(SSS)
△EBO≌△FCO(AAS)
(2)图中有哪些相等的线段?
(3)图中有哪些相等的角?
6、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有(
)
A.1对
B.2对
C.3对
D.4对
D
O
D
B
E
C
A
1
2
阅读下题及其说理过程:
已知:如图,D是⊿ABC中BC边上的中点,EB=EC,∠ABE=∠ACE,说明∠BAE=∠CAE的理由。
解:在AEB和AEC中
EB=EC
∠ABE=∠ACE
AE=AE
∴⊿AEB≌∠AEC
∴∠BAE=∠CAE
A
B
C
D
E
问:上面说理过程是否正确?若正确,请写出每一步的推理根据;若不正确,请指出错在哪一步,并写出你认为正确的推理过程.
例1、已知如图,AB=AC,AO平分∠BAC,请说明(1)△ABO≌△ACO;(2)DO=EO的理由.
A
B
C
O
D
E
1
2
3
4
解(1)∵
AO平分∠BAC
∴∠1=∠2
(已知)
(角平分线定义)
在△ABO和△ACO中
AB=AC
AO=AO
(已知)
(公共边)
∴
△ABO≌△ACO
(SAS)
(2)∵△ABO≌△ACO
∴
∠B=∠C
OB=0C
(全等三角形的对应角、对应边相等)
∠1=∠2
在△BOD和△COE中
∠3=
∠4
OB=0C
∠B=∠C
(对顶角相等)
∴
△BOD≌△COE
(ASA)
∴DO=EO
(全等三角形的对应边相等)
例2、如图,AD是△ABC的高,且AD平分∠BAC,
请指出∠B与∠C的关系,并说明理由。
A
B
C
D
解:∵AD是△ABC的高
∴∠ADB=∠ADC=90°
∵AD平分∠BAC
∴∠BAD=∠CAD
在△ABD和△ACD中,
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
∴
△ABD≌
△ACD
∴∠B=∠C
八上
1.53课后
No.10
证明:∵AD是△ABC的高,
∴∠ADC=
90°∴∠DAC+∠C
=
90°
同理∠EBC+∠C
=
90°,
∴∠DAC=∠EBC.
∵AD=BD,∠BDH=∠ADC
=
90°,
∴ΔBDH≌ΔADC.
八上
1.54提高
No.11
(1)提示:证明△ABD≌△CAE,
∴AD=CE,BD=AE,
∴BD=AE=AD+DE=CE+DE;
八上
1.54提高
No.12
(2)BD=DE-CE,
提示:证明△ABD≌△CAE
C
B
D
E
ΔCBD≌ΔABE
A
CB
=
AB
S
S
BD=BE
A
∠CBD
=
∠ABE
∠EBD
-∠EBC
=
∠ABC
-∠EBC
∠EBD
=
∠ABC
=
60°
例3、如图,已知:ΔABC和ΔBDE是等边三角形,D在AE的延长线上。求证:ΔCBD≌ΔABE
A
B
C
D
E
变式1、如图,已知:ΔABC和ΔBDE是等边三角形,D在AE的延
长线上。
求证:BD
+
DC
=
AD
A
C
D
E
B
ΔCBD
≌
ΔABE
∠CBA+
∠DBA
=
∠EBD+
∠DBA
∠CBA=
∠EBD=
60°
CB=
AB
DB
=
EB
∠CBD=
∠ABE
变式2、如图,已知:点C、B、E在同一条直线上,ΔABC和ΔBDE是等边三角形。
求证:
ΔCBD≌ΔABE
A
C
D
E
B
G
H
变式3、
如图,已知△ABC和△DEB等边三角形
。C,B,E在一条直线上
求证:
BG
=
BH。
八上
1.6课后
No.9
连结AB,BC,
分别作线段AB,BC的垂直平分线,
交点的位置就是学校的位置
例4、如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB,②AE=CF,③∠B=∠D,④
∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
A
B
C
D
E
F
B
A
F
C
D
E
1、如图,已知AB=ED,AF=CD,EF=BC,
说明∠EFD=∠BCA的理由。
2、如图,∠1=∠2,AB=CD,AC与BD相交于点O,则图中必定全等的三角形有(
)
A.
2对
B.
3对
C.
4对
D.
6对
A
O
D
C
B
1
2
C
巩固练习:
A
C
B
O
D
3.如图:AC和DB相交于点O,若AB=DC,AC=DB,则∠B=∠C,请说明理由.
(提示:连结AD)
4.如图,在△ABC中,
AD是△BAC的角平分线,DE是△ABD的高线,
∠C=90
度。若DE=2,BD=3,求线段BC的长。
B
D
E
A
C
5、如下图,已知△ABC中,DE是BC边上的中垂线,若AC=5,EC=2,
△ADC的周长是13,求△ABC的周长。
A
B
C
D
E
6、如上图,EF是AB的中垂线,分别延长BE、AE至D,C,使DE=CE,则AD与BC相等吗?
请说明理由。
A
B
C
D
E
F
A
B
C
D
E
7、如下图,已知AD是△ABC的中线,CE是△ADC的中线,若△ABC的面积是8,求△DEC的面积。
8、如上图,△ABC中,点D是BC上的一点,点E是AD上的一点,若BD:CD=2:3,DE:AE=1:4,△ABC的面积是8,求△DEC的面积。
A
B
C
D
E
要想知道一个池塘的两岸上最远两点之间的距离,没有船,且不能直接去测量。如果只用绳子和尺子,怎样才能测出它们之间的距离呢?
它们之间有多远呢?
方案设计
A
B
A
B
C
E
D
ABC≌ DEC(SAS)
AB = DE
在
ABC与
DEC中,
AC = DC
∠ACB=∠DCE
BC = EC
先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离。
方案一
△
ACD≌
△
CAB(SAS)
AB
=
CD
方
案
二
B
C
A
D
1
2
∠1=∠2
AD=CB
AC=CA
解:连结AC,由AD∥CB,可得∠1=∠2
在△ACD与△CAB中
如图,先作三角形ABC,再找一点D,使AD∥BC,并使AD=BC,连结CD,量CD的长即得AB的长
方案三
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长。
B
A
D
C
解:
在Rt ADB与Rt CDB中
ADB≌ CDB(SAS)
∴
BA
=
BC
BD=BD
∠ADB=∠CDB
CD=AD
1、已知钝角△ABC,求作:
(1)AC边上的中线;
(2)∠C的角平分线;
(3)
BC边上的高。
A
B
C
作图类:
2、已知线段a、b、c,作△ABC,使AB=c,AC=b,BC=a。
a
c
b
3、已知线段a、b、∠α,作△ABC,使AB=a,AC=b,∠A=
∠α
。
a
b
α
4、已知线段a、∠α
∠β
、,作△ABC,使AB=a,∠A=
∠α,
∠A=
∠
β
。
a
α
β
回顾、反思
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
