2020年秋浙教版八年级数学上册第1章三角形的初步认识单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020年秋浙教版八年级数学上册第1章三角形的初步认识单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 287.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-09 11:13:04 | ||
图片预览


文档简介
2020年秋浙教版八年级数学上册第1章三角形的初步认识单元测试卷
一、选择题(共10题;共30分)
1.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取(??
)
A.?10cm????????????????????B.?5cm??????????????????C.?20cm??????????????????????D.?25cm
2.能说明“锐角
,锐角
的和是锐角”是假命题的例证图是(??
).
A.?????B.??????C.???????D.?
3.如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于
EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
A.?AO平分∠EAF???????B.?AO垂直平分EF?????????C.?GH垂直平分EF????????D.?GH平分AF
4.将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是(??
)
A.?90°??????????????B.?120°?????????????C.?135°???????????????????????D.?150°
5.下列说法中正确的是(??
)
A.?面积相等的两个图形是全等形????????????????????????????B.?周长相等的两个图形是全等形
C.?所有正方形都是全等形??????????????????????????????????????D.?能够完全重合的两个图形是全等形
6.如图,在
中,
,
,如果
平分
,那么
的度数是(???
)
A.????????????????B.?????????????????????C.??????????????????????????D.?
7.如图,已知
,
,下列条件中不能判定
≌
的是(??
)
A.??????????????B.???????????C.??????????????????D.?
8.如图,直线
于点E,若
,则
的度数是(???
)
A.?120°???????B.?100°????????????C.?150°????????????D.?160°
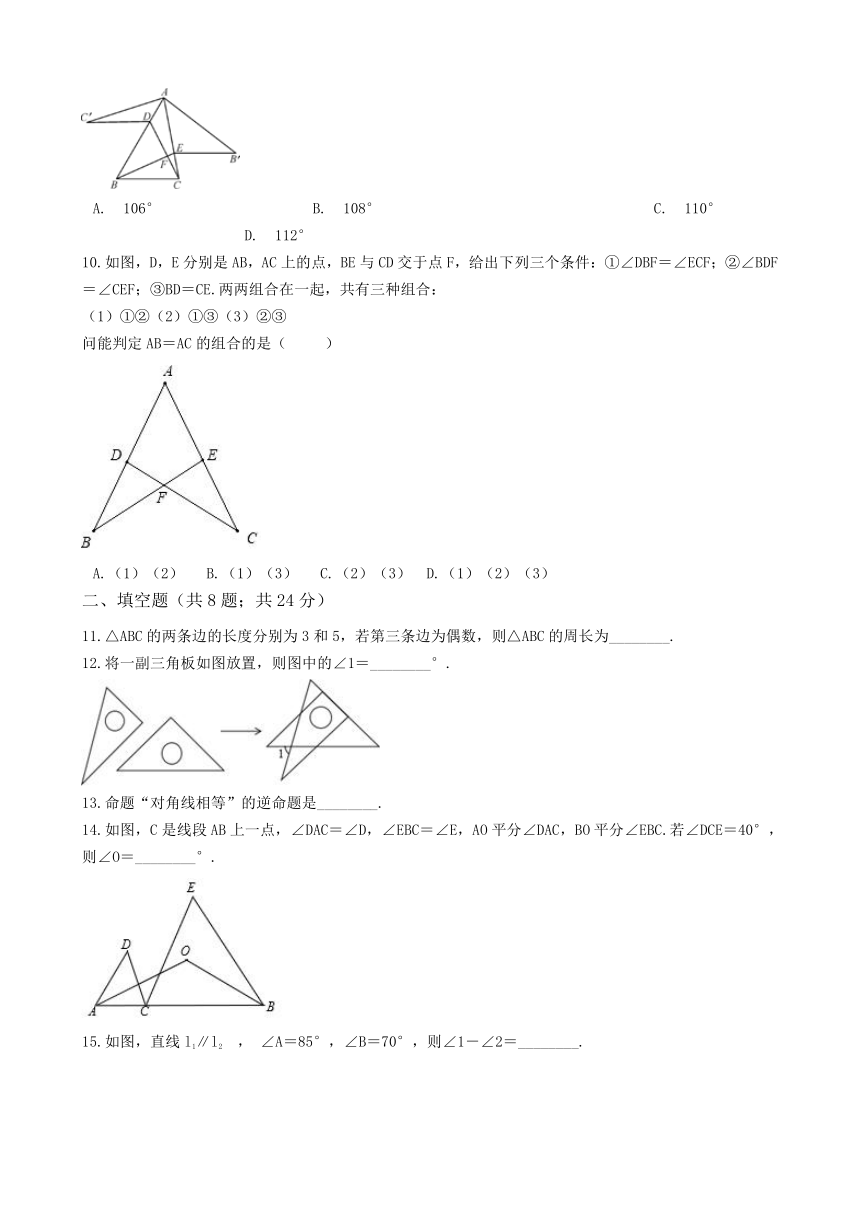
9.如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE,CD交于点F.若∠BAC=35°,则∠BFC的大小是(???
)
A.?106°??????????B.?108°??????????????????C.?110°?????????????D.?112°
10.如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF;③BD=CE.两两组合在一起,共有三种组合:
(1)①②(2)①③(3)②③
问能判定AB=AC的组合的是(??
)
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(1)(2)(3)
二、填空题(共8题;共24分)
11.△ABC的两条边的长度分别为3和5,若第三条边为偶数,则△ABC的周长为________.
12.将一副三角板如图放置,则图中的∠1=________°.
13.命题“对角线相等”的逆命题是________.
14.如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=________°.
15.如图,直线l1∥l2
,
∠A=85°,∠B=70°,则∠1-∠2=________.
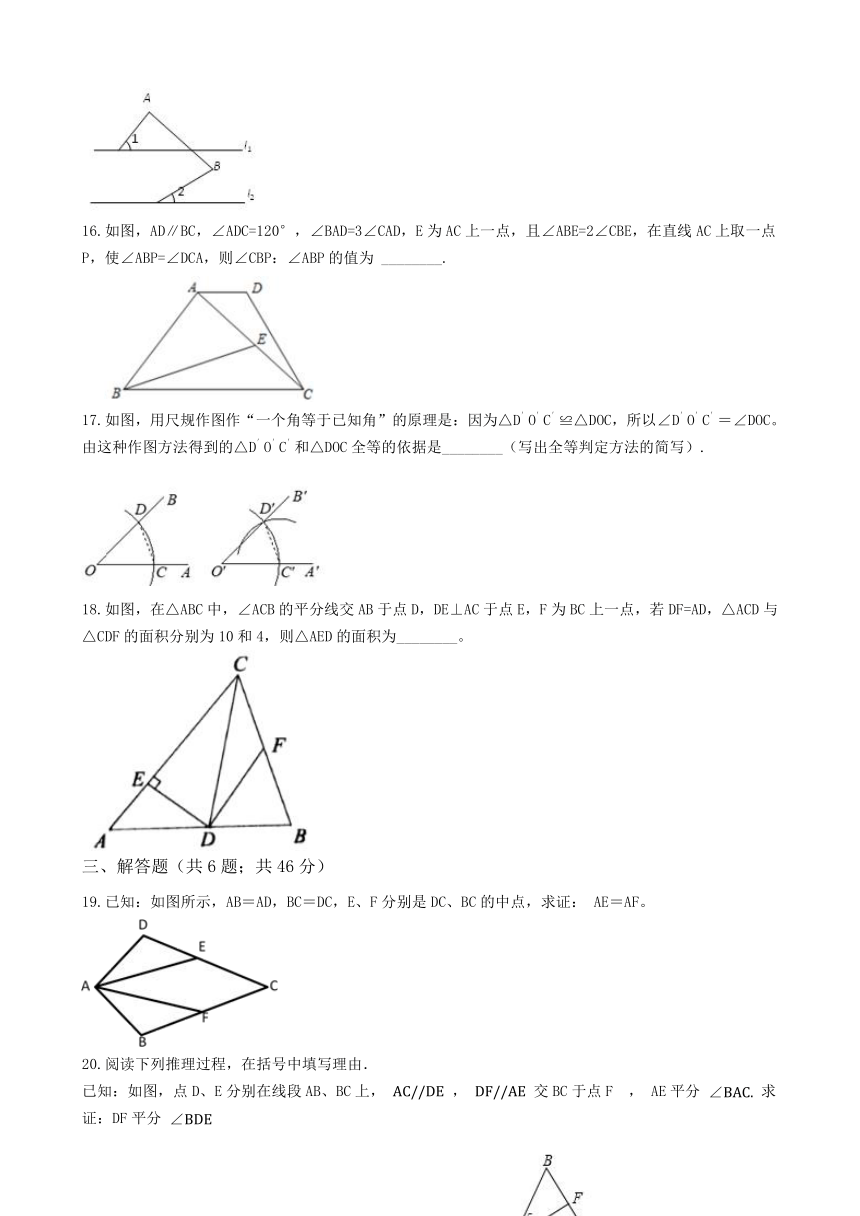
16.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
________.
?
17.如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是________(写出全等判定方法的简写).
18.如图,在△ABC中,∠ACB的平分线交AB于点D,DE⊥AC于点E,F为BC上一点,若DF=AD,△ACD与△CDF的面积分别为10和4,则△AED的面积为________。
三、解答题(共6题;共46分)
19.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:
AE=AF。
20.阅读下列推理过程,在括号中填写理由.
已知:如图,点D、E分别在线段AB、BC上,
,
交BC于点F
,
AE平分
求证:DF平分
证明:
平分
已知
?(????????????????????????
)
????????????????????????
故
(????????????????????????
)
?(????????????????????????
)
并且
(????????????????????????
)
?(????????????????????????
)
平分
(????????????????????????
)
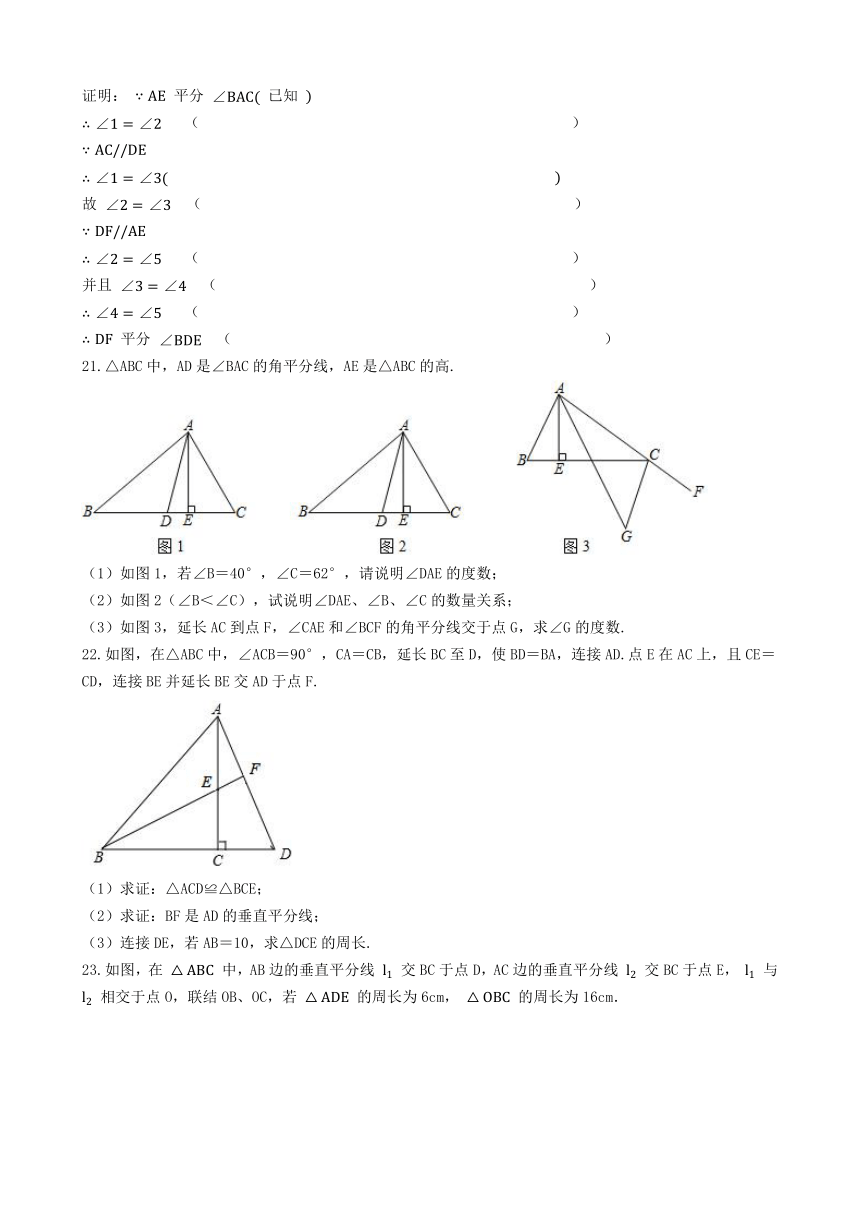
21.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
22.如图,在△ABC中,∠ACB=90°,CA=CB,延长BC至D,使BD=BA,连接AD.点E在AC上,且CE=CD,连接BE并延长BE交AD于点F.
(1)求证:△ACD≌△BCE;
(2)求证:BF是AD的垂直平分线;
(3)连接DE,若AB=10,求△DCE的周长.
23.如图,在
中,AB边的垂直平分线
交BC于点D,AC边的垂直平分线
交BC于点E,
与
相交于点O,联结OB、OC,若
的周长为6cm,
的周长为16cm.
(1)求线段BC的长;
(2)联结OA,求线段OA的长;
(3)若
,求
的度数.
24.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE________CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:________.
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
________,使①中的两个结论仍然成立,并证明两个结论成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明。
答案
一、选择题
1.解:设第三边为x,根据三角形的三边关系,则有:
x<10+15,
即x<25,
故不可能取25cm长的木棍作为三角形的第三边,
故答案为:D.
2.解:A、如图1,∠1是锐角,且∠1=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意;
?
B、如图2,∠2是锐角,且∠2=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意;
C、如图3,∠3是钝角,且∠3=
,所以此图说明“锐角
,锐角
的和是锐角”是假命题,故本选项符合题意;
D、如图4,∠4是锐角,且∠4=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意.
故答案为:C.
3.解:由尺规作图的痕迹可得:GH垂直平分线段EF.
故答案为:C.
4.解:如图,
∵含30°、45°的直角三角形,
∴∠ACB=∠E=90°,∠DFC=30°,
∠1=∠ACB+∠DFC=90°+30°=120°.
故答案为:B.
5.因为能够完全重合的两个图形是全等形,所以选D.
6.解:
?
平分
,
?
?
故答案为:C.
7.A、∠M=∠N,符合AAS,能判定△ABM≌△CDN;
B、MB=ND,符合SAS,能判定△ABM≌△CDN;
C、AM=CN,有SSA,不能判定△ABM≌△CDN;
D、AM∥CN,得出∠MAB=∠NCD,符合ASA,能判定△ABM≌△CDN,
故答案为:C.
8.解:延长AE,与DC的延长线交于点F,
∵AB∥CD,
∴∠A+∠AFC=180°,
∵
,
∴∠AFC=60°,
∵AE⊥CE,
∴∠AEC=90°,
而∠AEC=∠AFC+∠ECF,
∴∠ECF=∠AEC-∠F
=30°,
∴∠ECD=180°-30°=150°,
故答案为:C.
9.设
,
,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴
,
,
,
∴
,
,
∴
,即
,
则
,
∵
,
∴
.
故答案为:C.
10.解:能判定AB=AC的组合的是(2)(3),理由如下:(1)①∠DBF=∠ECF;②∠BDF=∠CEF,
不能证明△ABE≌△ACD,没有相等的边;
∴不能判定AB=AC;(2)①∠DBF=∠ECF;③BD=CE,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
∴BF=CF,DF=EF,
∴BE=CD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC;(3)②∠BDF=∠CEF;③BD=CE,
同(2)得:△BDF≌△CEF(AAS),
∴∠DBF=∠ECF,BF=CF,DF=EF,
∴BE=CD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC;
故答案为:C.
二、填空题
11.解:∵根据三角形的三边关系可知,三角形中任意两边之和大于第三边,任意两边之差小于第三边,且已知两边的长度为3、5,
∴设第三边长度为x,第三边长度要满足:2故x的取值有两种情况:①x=4,
ABC的周长为3+4+5=12;
②x=6,
ABC的周长为3+6+5=14,
故答案为:12或14.
12.解:如图,
根据三角板的性质知:∠BAC=∠ACD=90?,∠B=45?,∠D=30?,
∴AB∥CD,
∴∠BED=∠B=45?,
∴∠1=∠BED+∠D=45?+30?=75?,
故答案为:75.
13.解:命题“对角线相等”的逆命题是:如果有两条线段相等,那么这两条线段是对角线.
故答案为:如果有两条线段相等,那么这两条线段是对角线.
14.解:
,
,
,
,
,
,
平分
,
平分
,
,
,
故答案为:125.
15.解:过点B作BC∥l1
,
如图所示:
∴∠CBA=∠ADF,
∵直线l1∥l2
,
∴BC∥l2
,
∴∠2=∠EBC,
∵∠B=∠EBC+∠CBA=70°,
∴∠2+∠ADF=70°,即∠ADF=70°﹣∠2,
∵∠1+∠A+∠ADF=180°,
∴∠1+85°+70°﹣∠2=180°,
∴∠1﹣∠2=25°.
故答案为25°.
16.解:如图,
①当∠ABP1=∠DCA时,
∵∠D=120°,
∴∠ACD+∠DAC=180°?120°=60°,??
∵∠BAD=3∠CAD,∠ABE=2∠CBE,
∴∠ABC=3∠CBE
∵AD∥BC,
∴∠BAD+∠ABC=180°
∴3∠DAC+3∠EBC=180°,
∴∠DAC+∠EBC=60°,
∴∠EBC=∠ACD=∠ABP1=∠P1BE,
∴∠CBP1:∠ABP1=2,
②当∠ABP2=∠DCA时,
∴∠CBP2:∠ABP2=4,
故答案为:2或4.
17.解:由作图的痕迹可知,
∴
△D′O′C′≌△DOC
(SAS),
∴
∠D′O′C′=∠DOC
.
故答案为:SSS.
18.解:如图,过点D作DG⊥BC于点G,
∵DE⊥AC,CD平分∠ACB,
∴DE=DG,∠AED=∠DGF=90°,
在Rt△AED和Rt△DGF中
∴Rt△AED≌Rt△DGF(HL);
∴S△AED=S△DGF
,
同理可证:S△CED=S△DGC
,
∵S△ADC=S△ADE+S△CED
=S△ADE+S△DGC
=S△ADE+S△CDF+S△DFG
=S△ADE+S△CDF+S△ADE
∴2S△ADE+4=10
解之:S△ADE=3.
故答案为:3.
三、解答题
19.
证明:连接AC,
在△ACD和△ACB中,
,
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF,
∵BC=DC,E,F分别是DC、BC的中点,
∴CE=CF,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SAS),
∴AE=AF.
20.
证明:
平分
已知
角平分线的定义
已知
两直线平行,内错角相等
故
等量代换
已知
,
两直线平行,同位角相等
两直线平行,内错角相等
等量代换
平分
角平分线的定义
.
故答案为:角平分线的定义,两直线平行,内错角相等,等量代换,两直线平行,同位角相等,等量代换,角平分线的定义.
21.(1)解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,
∵AD是∠BAC的平分线,
∴∠DAC=
∠BAC=39°,
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C=90°﹣62°=28°,
∴∠DAE=∠DAC﹣∠EAC=39°﹣28°=11°
(2)解:∵∠BAC=180°﹣∠B﹣∠C,
∵AD是∠BAC的平分线,
∴∠DAC=
∠BAC=90°﹣
(∠B+∠C),
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣
(∠B+∠C)﹣(90°﹣∠C)=
(∠C﹣∠B)
(3)解:设∠ACB=α,
∵AE⊥BC,
∴∠EAC=90°﹣α,∠BCF=180°﹣α,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=
EAC=
(90°﹣α)=45°﹣
,∠BCG=
BCF=
(180°﹣α)=90°﹣
,
∴∠G=180°﹣∠GAC﹣∠ACG=180°﹣(45°﹣
)﹣α﹣(90°﹣
)=45°.
22.
(1)证明:∵∠ACB=90°,CD是BC延长线,
∴∠ACD=∠ACB=90°.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)证明:由(1)知△ACD≌△BCE则∠CAD=∠CBE,
又∵∠AEF=∠BEC,
∴在△AEF与△BEC中∠AFE=∠BCE=90°,
∴BF⊥AD,
又∵BD=BA,
∴BF是AD的垂直平分线.
(3)解:∵EF是AD的垂直平分线,
∴EA=ED,
又∵BC=AC,AB=BD=10,
∴△DEC的周长=ED+EC+CD=AC+CD=BC+CD=AB=10.
23.(1)∵
是边AB的垂直平分线,∴
.
∵
是边AC的垂直平分线,
∴
.∴
.
(2)如图,
∵
是边AB的垂直平分线,∴
.
∵
是边AC的垂直平分线,∴
.
∵
,∴
.
(3)∵
,∴
.
∵
,
,∴
,
.
∴
.
24.(1)=;=;条件EF=|BE?AF|
证明:在△BCE中,∠CBE+∠BCE=180°?∠BEC=180°?∠α.
∵∠BCA=180°?∠α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF,
又∵BC=CA,∠BEC=∠CFA,
∴△BCE≌△CAF(AAS)
∴BE=CF,CE=AF,
又∵EF=CF?CE,
∴EF=|BE?AF|.
(2)解:猜想:EF=BE+AF.
证明过程:
∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,
∴∠BCE=∠CAF,
又∵BC=CA,
∴△BCE≌△CAF(AAS).
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.
故答案为:EF=BE+AF.
解:(1)①∵∠BCA=90
,∠α=90
,
∴∠BCE+∠CBE=90
,∠BCE+∠ACF=90
,
∴∠CBE=∠ACF,
∵CA=CB,∠BEC=∠CFA;
∴△BCE≌△CAF,
∴BE=CF;EF=|CF?CE|=|BE?AF|.
故答案为:=,=;
一、选择题(共10题;共30分)
1.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取(??
)
A.?10cm????????????????????B.?5cm??????????????????C.?20cm??????????????????????D.?25cm
2.能说明“锐角
,锐角
的和是锐角”是假命题的例证图是(??
).
A.?????B.??????C.???????D.?
3.如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于
EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
A.?AO平分∠EAF???????B.?AO垂直平分EF?????????C.?GH垂直平分EF????????D.?GH平分AF
4.将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是(??
)
A.?90°??????????????B.?120°?????????????C.?135°???????????????????????D.?150°
5.下列说法中正确的是(??
)
A.?面积相等的两个图形是全等形????????????????????????????B.?周长相等的两个图形是全等形
C.?所有正方形都是全等形??????????????????????????????????????D.?能够完全重合的两个图形是全等形
6.如图,在
中,
,
,如果
平分
,那么
的度数是(???
)
A.????????????????B.?????????????????????C.??????????????????????????D.?
7.如图,已知
,
,下列条件中不能判定
≌
的是(??
)
A.??????????????B.???????????C.??????????????????D.?
8.如图,直线
于点E,若
,则
的度数是(???
)
A.?120°???????B.?100°????????????C.?150°????????????D.?160°
9.如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE,CD交于点F.若∠BAC=35°,则∠BFC的大小是(???
)
A.?106°??????????B.?108°??????????????????C.?110°?????????????D.?112°
10.如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF;③BD=CE.两两组合在一起,共有三种组合:
(1)①②(2)①③(3)②③
问能判定AB=AC的组合的是(??
)
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(1)(2)(3)
二、填空题(共8题;共24分)
11.△ABC的两条边的长度分别为3和5,若第三条边为偶数,则△ABC的周长为________.
12.将一副三角板如图放置,则图中的∠1=________°.
13.命题“对角线相等”的逆命题是________.
14.如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=________°.
15.如图,直线l1∥l2
,
∠A=85°,∠B=70°,则∠1-∠2=________.
16.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
________.
?
17.如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC。由这种作图方法得到的△D′O′C′和△DOC全等的依据是________(写出全等判定方法的简写).
18.如图,在△ABC中,∠ACB的平分线交AB于点D,DE⊥AC于点E,F为BC上一点,若DF=AD,△ACD与△CDF的面积分别为10和4,则△AED的面积为________。
三、解答题(共6题;共46分)
19.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:
AE=AF。
20.阅读下列推理过程,在括号中填写理由.
已知:如图,点D、E分别在线段AB、BC上,
,
交BC于点F
,
AE平分
求证:DF平分
证明:
平分
已知
?(????????????????????????
)
????????????????????????
故
(????????????????????????
)
?(????????????????????????
)
并且
(????????????????????????
)
?(????????????????????????
)
平分
(????????????????????????
)
21.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
22.如图,在△ABC中,∠ACB=90°,CA=CB,延长BC至D,使BD=BA,连接AD.点E在AC上,且CE=CD,连接BE并延长BE交AD于点F.
(1)求证:△ACD≌△BCE;
(2)求证:BF是AD的垂直平分线;
(3)连接DE,若AB=10,求△DCE的周长.
23.如图,在
中,AB边的垂直平分线
交BC于点D,AC边的垂直平分线
交BC于点E,
与
相交于点O,联结OB、OC,若
的周长为6cm,
的周长为16cm.
(1)求线段BC的长;
(2)联结OA,求线段OA的长;
(3)若
,求
的度数.
24.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE________CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:________.
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
________,使①中的两个结论仍然成立,并证明两个结论成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明。
答案
一、选择题
1.解:设第三边为x,根据三角形的三边关系,则有:
x<10+15,
即x<25,
故不可能取25cm长的木棍作为三角形的第三边,
故答案为:D.
2.解:A、如图1,∠1是锐角,且∠1=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意;
?
B、如图2,∠2是锐角,且∠2=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意;
C、如图3,∠3是钝角,且∠3=
,所以此图说明“锐角
,锐角
的和是锐角”是假命题,故本选项符合题意;
D、如图4,∠4是锐角,且∠4=
,所以此图说明“锐角
,锐角
的和是锐角”是真命题,故本选项不符合题意.
故答案为:C.
3.解:由尺规作图的痕迹可得:GH垂直平分线段EF.
故答案为:C.
4.解:如图,
∵含30°、45°的直角三角形,
∴∠ACB=∠E=90°,∠DFC=30°,
∠1=∠ACB+∠DFC=90°+30°=120°.
故答案为:B.
5.因为能够完全重合的两个图形是全等形,所以选D.
6.解:
?
平分
,
?
?
故答案为:C.
7.A、∠M=∠N,符合AAS,能判定△ABM≌△CDN;
B、MB=ND,符合SAS,能判定△ABM≌△CDN;
C、AM=CN,有SSA,不能判定△ABM≌△CDN;
D、AM∥CN,得出∠MAB=∠NCD,符合ASA,能判定△ABM≌△CDN,
故答案为:C.
8.解:延长AE,与DC的延长线交于点F,
∵AB∥CD,
∴∠A+∠AFC=180°,
∵
,
∴∠AFC=60°,
∵AE⊥CE,
∴∠AEC=90°,
而∠AEC=∠AFC+∠ECF,
∴∠ECF=∠AEC-∠F
=30°,
∴∠ECD=180°-30°=150°,
故答案为:C.
9.设
,
,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴
,
,
,
∴
,
,
∴
,即
,
则
,
∵
,
∴
.
故答案为:C.
10.解:能判定AB=AC的组合的是(2)(3),理由如下:(1)①∠DBF=∠ECF;②∠BDF=∠CEF,
不能证明△ABE≌△ACD,没有相等的边;
∴不能判定AB=AC;(2)①∠DBF=∠ECF;③BD=CE,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
∴BF=CF,DF=EF,
∴BE=CD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC;(3)②∠BDF=∠CEF;③BD=CE,
同(2)得:△BDF≌△CEF(AAS),
∴∠DBF=∠ECF,BF=CF,DF=EF,
∴BE=CD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC;
故答案为:C.
二、填空题
11.解:∵根据三角形的三边关系可知,三角形中任意两边之和大于第三边,任意两边之差小于第三边,且已知两边的长度为3、5,
∴设第三边长度为x,第三边长度要满足:2
ABC的周长为3+4+5=12;
②x=6,
ABC的周长为3+6+5=14,
故答案为:12或14.
12.解:如图,
根据三角板的性质知:∠BAC=∠ACD=90?,∠B=45?,∠D=30?,
∴AB∥CD,
∴∠BED=∠B=45?,
∴∠1=∠BED+∠D=45?+30?=75?,
故答案为:75.
13.解:命题“对角线相等”的逆命题是:如果有两条线段相等,那么这两条线段是对角线.
故答案为:如果有两条线段相等,那么这两条线段是对角线.
14.解:
,
,
,
,
,
,
平分
,
平分
,
,
,
故答案为:125.
15.解:过点B作BC∥l1
,
如图所示:
∴∠CBA=∠ADF,
∵直线l1∥l2
,
∴BC∥l2
,
∴∠2=∠EBC,
∵∠B=∠EBC+∠CBA=70°,
∴∠2+∠ADF=70°,即∠ADF=70°﹣∠2,
∵∠1+∠A+∠ADF=180°,
∴∠1+85°+70°﹣∠2=180°,
∴∠1﹣∠2=25°.
故答案为25°.
16.解:如图,
①当∠ABP1=∠DCA时,
∵∠D=120°,
∴∠ACD+∠DAC=180°?120°=60°,??
∵∠BAD=3∠CAD,∠ABE=2∠CBE,
∴∠ABC=3∠CBE
∵AD∥BC,
∴∠BAD+∠ABC=180°
∴3∠DAC+3∠EBC=180°,
∴∠DAC+∠EBC=60°,
∴∠EBC=∠ACD=∠ABP1=∠P1BE,
∴∠CBP1:∠ABP1=2,
②当∠ABP2=∠DCA时,
∴∠CBP2:∠ABP2=4,
故答案为:2或4.
17.解:由作图的痕迹可知,
∴
△D′O′C′≌△DOC
(SAS),
∴
∠D′O′C′=∠DOC
.
故答案为:SSS.
18.解:如图,过点D作DG⊥BC于点G,
∵DE⊥AC,CD平分∠ACB,
∴DE=DG,∠AED=∠DGF=90°,
在Rt△AED和Rt△DGF中
∴Rt△AED≌Rt△DGF(HL);
∴S△AED=S△DGF
,
同理可证:S△CED=S△DGC
,
∵S△ADC=S△ADE+S△CED
=S△ADE+S△DGC
=S△ADE+S△CDF+S△DFG
=S△ADE+S△CDF+S△ADE
∴2S△ADE+4=10
解之:S△ADE=3.
故答案为:3.
三、解答题
19.
证明:连接AC,
在△ACD和△ACB中,
,
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF,
∵BC=DC,E,F分别是DC、BC的中点,
∴CE=CF,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SAS),
∴AE=AF.
20.
证明:
平分
已知
角平分线的定义
已知
两直线平行,内错角相等
故
等量代换
已知
,
两直线平行,同位角相等
两直线平行,内错角相等
等量代换
平分
角平分线的定义
.
故答案为:角平分线的定义,两直线平行,内错角相等,等量代换,两直线平行,同位角相等,等量代换,角平分线的定义.
21.(1)解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,
∵AD是∠BAC的平分线,
∴∠DAC=
∠BAC=39°,
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C=90°﹣62°=28°,
∴∠DAE=∠DAC﹣∠EAC=39°﹣28°=11°
(2)解:∵∠BAC=180°﹣∠B﹣∠C,
∵AD是∠BAC的平分线,
∴∠DAC=
∠BAC=90°﹣
(∠B+∠C),
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣
(∠B+∠C)﹣(90°﹣∠C)=
(∠C﹣∠B)
(3)解:设∠ACB=α,
∵AE⊥BC,
∴∠EAC=90°﹣α,∠BCF=180°﹣α,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=
EAC=
(90°﹣α)=45°﹣
,∠BCG=
BCF=
(180°﹣α)=90°﹣
,
∴∠G=180°﹣∠GAC﹣∠ACG=180°﹣(45°﹣
)﹣α﹣(90°﹣
)=45°.
22.
(1)证明:∵∠ACB=90°,CD是BC延长线,
∴∠ACD=∠ACB=90°.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)证明:由(1)知△ACD≌△BCE则∠CAD=∠CBE,
又∵∠AEF=∠BEC,
∴在△AEF与△BEC中∠AFE=∠BCE=90°,
∴BF⊥AD,
又∵BD=BA,
∴BF是AD的垂直平分线.
(3)解:∵EF是AD的垂直平分线,
∴EA=ED,
又∵BC=AC,AB=BD=10,
∴△DEC的周长=ED+EC+CD=AC+CD=BC+CD=AB=10.
23.(1)∵
是边AB的垂直平分线,∴
.
∵
是边AC的垂直平分线,
∴
.∴
.
(2)如图,
∵
是边AB的垂直平分线,∴
.
∵
是边AC的垂直平分线,∴
.
∵
,∴
.
(3)∵
,∴
.
∵
,
,∴
,
.
∴
.
24.(1)=;=;条件EF=|BE?AF|
证明:在△BCE中,∠CBE+∠BCE=180°?∠BEC=180°?∠α.
∵∠BCA=180°?∠α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF,
又∵BC=CA,∠BEC=∠CFA,
∴△BCE≌△CAF(AAS)
∴BE=CF,CE=AF,
又∵EF=CF?CE,
∴EF=|BE?AF|.
(2)解:猜想:EF=BE+AF.
证明过程:
∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,
∴∠BCE=∠CAF,
又∵BC=CA,
∴△BCE≌△CAF(AAS).
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.
故答案为:EF=BE+AF.
解:(1)①∵∠BCA=90
,∠α=90
,
∴∠BCE+∠CBE=90
,∠BCE+∠ACF=90
,
∴∠CBE=∠ACF,
∵CA=CB,∠BEC=∠CFA;
∴△BCE≌△CAF,
∴BE=CF;EF=|CF?CE|=|BE?AF|.
故答案为:=,=;
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
