3.2 图形的旋转 课件(17张PPT)
文档属性
| 名称 | 3.2 图形的旋转 课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1021.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-10 14:28:51 | ||
图片预览




文档简介
转动的车轮
转动的时针
荡秋千
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千、车轮在转动过程中,其形状、大小、位置是否发生变化呢?
【学习目标】
1.了解图形旋转的概念;
2.理解图形旋转的性质;
3.会按要求作出简单平面图形旋转后图形;
4.会应用旋转的性质解决简单的几何问题
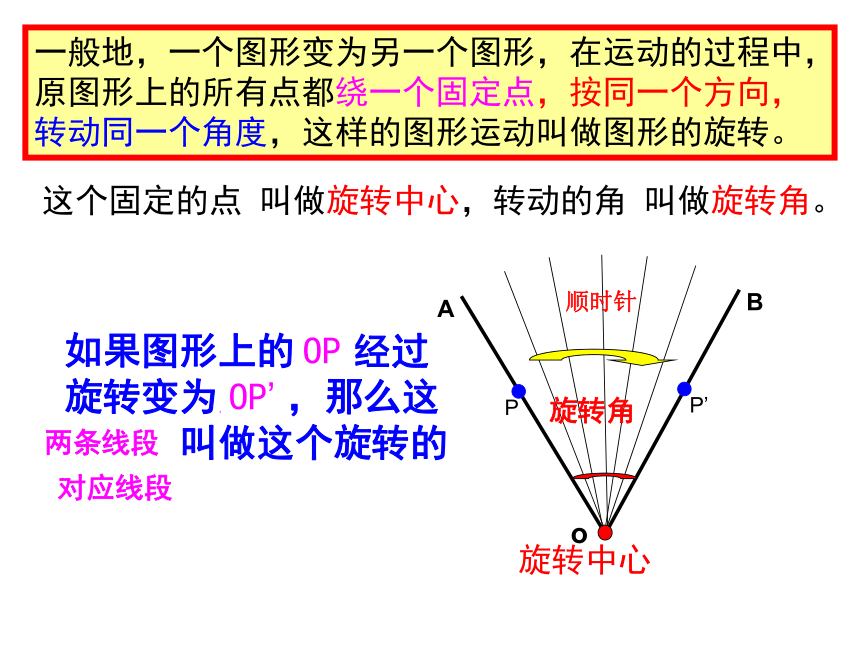
这个固定的点 叫做旋转中心,转动的角 叫做旋转角。
旋转角
旋转中心
一般地,一个图形变为另一个图形,在运动的过程中,原图形上的所有点都绕一个固定点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转。
A
o
B
P
P’
如果图形上的点P经过旋转变为点P’,那么这两个点叫做这个旋转的对应点。
OP
OP’
对应线段
两条线段
顺时针
举出一些现实生活中旋转的实例,并指出旋转中心,旋转方向和旋转角.
想一想
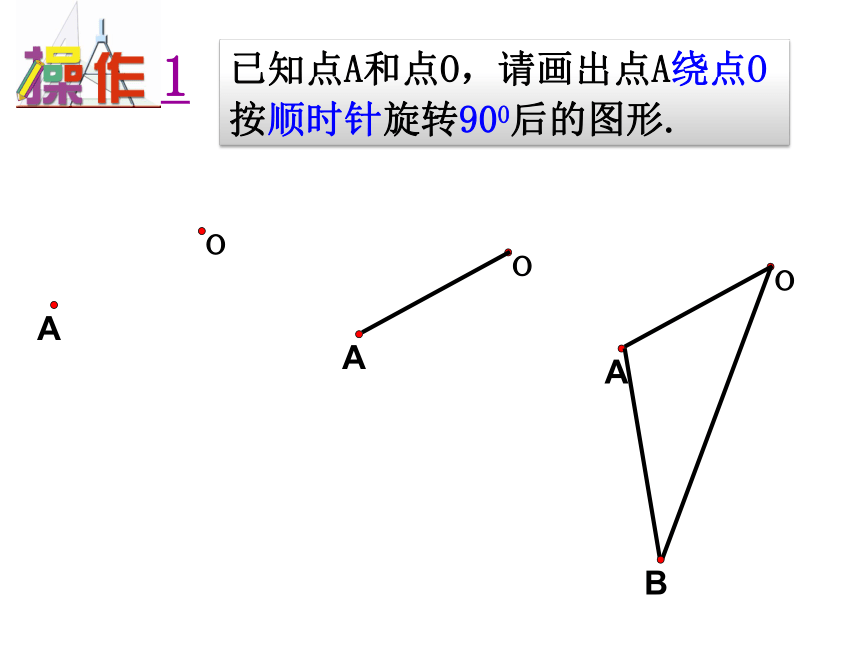
1
已知点A和点O,请画出点A绕点O按顺时针旋转900后的图形.
A
o
A
o
A
o
B
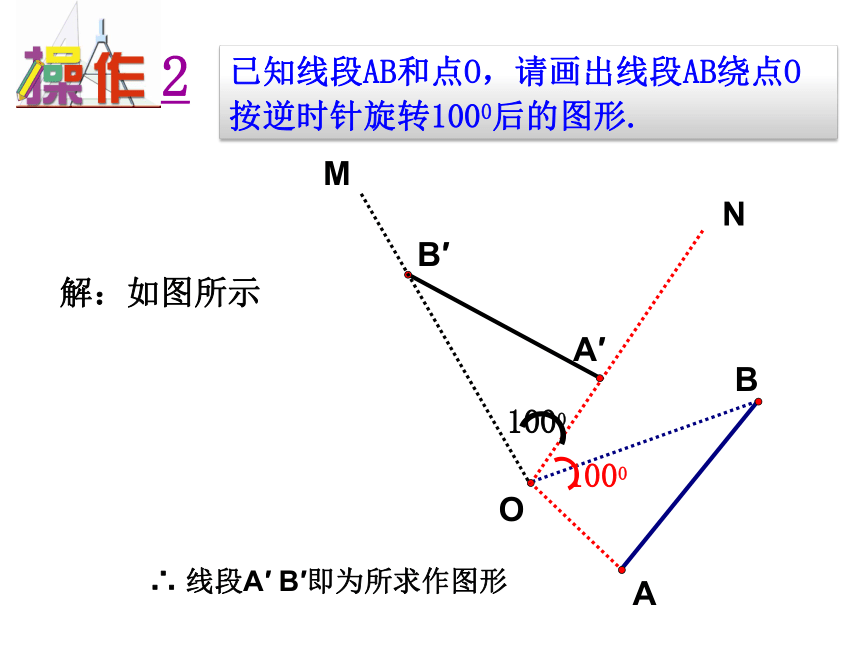
已知线段AB和点O,请画出线段AB绕点O按逆时针旋转1000后的图形.
N
A
B
O
B′
A′
M
⌒
1000
2
解:如图所示
∴ 线段A′ B′即为所求作图形
⌒
1000
例 如图,O是△ABC外一点,以点O为旋转中心,将△ABC按逆时针方向旋转60?,作出旋转后的图形.
3
∴ △A′ B′C′即为所求作图形
(1)原图形与图形旋转后所得的图形相比哪些改变了?哪些仍不变?
图形旋转:图形的形状、大小不改变;
(2)经过旋转,点A、B、C分别运动到哪个位置?
对应点A—A’ ,B—B’ ,C—C’
(3)AO与A’O的长有什么关系?BO与BO’呢?CO与CO’呢?
对应点到旋转中心的距离相等
(4)∠AOA’、 ∠BOB’、 ∠COC’的角度与旋转角度有何关系?
对应点与旋转中心连线所成的角度等于旋转的角度
图形的方向改变
1.图形旋转所得的图形和原图形全等.
2.对应点到旋转中心的距离相等.
3. 任意一对对应点与旋转中心的连线所成的角度等于旋转角度.
1、如图:M为正方形ABCD的边DA的中点,把三角形MAB旋转到三角形NAD的位置.
(1)找出在这个过程中的旋转中心,旋转方向,旋转角度.
(2)指出线段DN的对应线段, ∠N的对应角.
2、如图,在四边形ABCD中, ∠ADC= ∠ABC= 90?,
AD=CD,DP、AB交于点P,若四边形ABCD的面积为16,求DP的长.
DP=4
1、相同:都是一种运动;运动前后不改变图形的形状和大小
2、
形状
大小
方向
轴对称
不变
不变
改变
平移
不变
不变
不变
旋转
不变
不变
改变
1.如图所示,∠AOB=90°,∠B=30°,△A′OB′可以看作是由 △AOB绕点O逆时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是 ( )
A.30° B.45°C.60° D.90°
3.
2.
转动的时针
荡秋千
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千、车轮在转动过程中,其形状、大小、位置是否发生变化呢?
【学习目标】
1.了解图形旋转的概念;
2.理解图形旋转的性质;
3.会按要求作出简单平面图形旋转后图形;
4.会应用旋转的性质解决简单的几何问题
这个固定的点 叫做旋转中心,转动的角 叫做旋转角。
旋转角
旋转中心
一般地,一个图形变为另一个图形,在运动的过程中,原图形上的所有点都绕一个固定点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转。
A
o
B
P
P’
如果图形上的点P经过旋转变为点P’,那么这两个点叫做这个旋转的对应点。
OP
OP’
对应线段
两条线段
顺时针
举出一些现实生活中旋转的实例,并指出旋转中心,旋转方向和旋转角.
想一想
1
已知点A和点O,请画出点A绕点O按顺时针旋转900后的图形.
A
o
A
o
A
o
B
已知线段AB和点O,请画出线段AB绕点O按逆时针旋转1000后的图形.
N
A
B
O
B′
A′
M
⌒
1000
2
解:如图所示
∴ 线段A′ B′即为所求作图形
⌒
1000
例 如图,O是△ABC外一点,以点O为旋转中心,将△ABC按逆时针方向旋转60?,作出旋转后的图形.
3
∴ △A′ B′C′即为所求作图形
(1)原图形与图形旋转后所得的图形相比哪些改变了?哪些仍不变?
图形旋转:图形的形状、大小不改变;
(2)经过旋转,点A、B、C分别运动到哪个位置?
对应点A—A’ ,B—B’ ,C—C’
(3)AO与A’O的长有什么关系?BO与BO’呢?CO与CO’呢?
对应点到旋转中心的距离相等
(4)∠AOA’、 ∠BOB’、 ∠COC’的角度与旋转角度有何关系?
对应点与旋转中心连线所成的角度等于旋转的角度
图形的方向改变
1.图形旋转所得的图形和原图形全等.
2.对应点到旋转中心的距离相等.
3. 任意一对对应点与旋转中心的连线所成的角度等于旋转角度.
1、如图:M为正方形ABCD的边DA的中点,把三角形MAB旋转到三角形NAD的位置.
(1)找出在这个过程中的旋转中心,旋转方向,旋转角度.
(2)指出线段DN的对应线段, ∠N的对应角.
2、如图,在四边形ABCD中, ∠ADC= ∠ABC= 90?,
AD=CD,DP、AB交于点P,若四边形ABCD的面积为16,求DP的长.
DP=4
1、相同:都是一种运动;运动前后不改变图形的形状和大小
2、
形状
大小
方向
轴对称
不变
不变
改变
平移
不变
不变
不变
旋转
不变
不变
改变
1.如图所示,∠AOB=90°,∠B=30°,△A′OB′可以看作是由 △AOB绕点O逆时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是 ( )
A.30° B.45°C.60° D.90°
3.
2.
同课章节目录
