第4章 相似三角形单元测试卷(含解析)
文档属性
| 名称 | 第4章 相似三角形单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 11:04:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级数学上册单元测试卷
第4章
相似三角形
姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分)
与能组成比例的是
A.
?16:14
B.
13:12
C.
7:8
D.
13:15
如图,在中,,且,,则????
A.
B.
C.
D.
已知∽,的周长为3,的周长为1,则与的面积之比为
A.
3:1
B.
1:3
C.
9:1
D.
1:9
如图,在中,,且,,则BC等于
A.
10cm
B.
16cm
C.
12cm
D.
如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知,,且测得米,米,米,那么该古城墙的高度是
A.
6米
B.
8米
C.
18米
D.
24米
已知四边形ABCD∽四边形,四边形ABCD与四边形的周长分别为24,36,则它们对角线AC与的比为
A.
B.
C.
D.
直角坐标系中,,,以O为位似中心,按位似比为把缩小,则点E的对应点的坐标为?????
A.
或
B.
或
C.
D.
如图,在某圆锥形灯罩的轴截面中,,,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线在该房间水平地面上形成的最大圆面面积为平方米假设该水平地面足够大,则点O到此房间屋顶的距离约为
A.
米
B.
米
C.
米
D.
米
如图,已知?的三边长为a?,b?,c?,且?,若平行于三角形一边的直线l?将?的周长分成相等的两部分,设图中的小三角形、、的面积分别为,则的大小关系是???
.
A.
?
B.
C.
D.
如图,点A和点B都在坐标轴上,,M为AB的中点,,MP交y轴于点C,交x轴于点E,MQ交x轴于点D,交y轴于点F,在AB的左侧以M为中心旋转,设AD的长为,BC的长为n,则下列结论正确的是
A.
∽
B.
C.
∽
D.
二、填空题(本大题共8小题,共24.0分)
若,则.
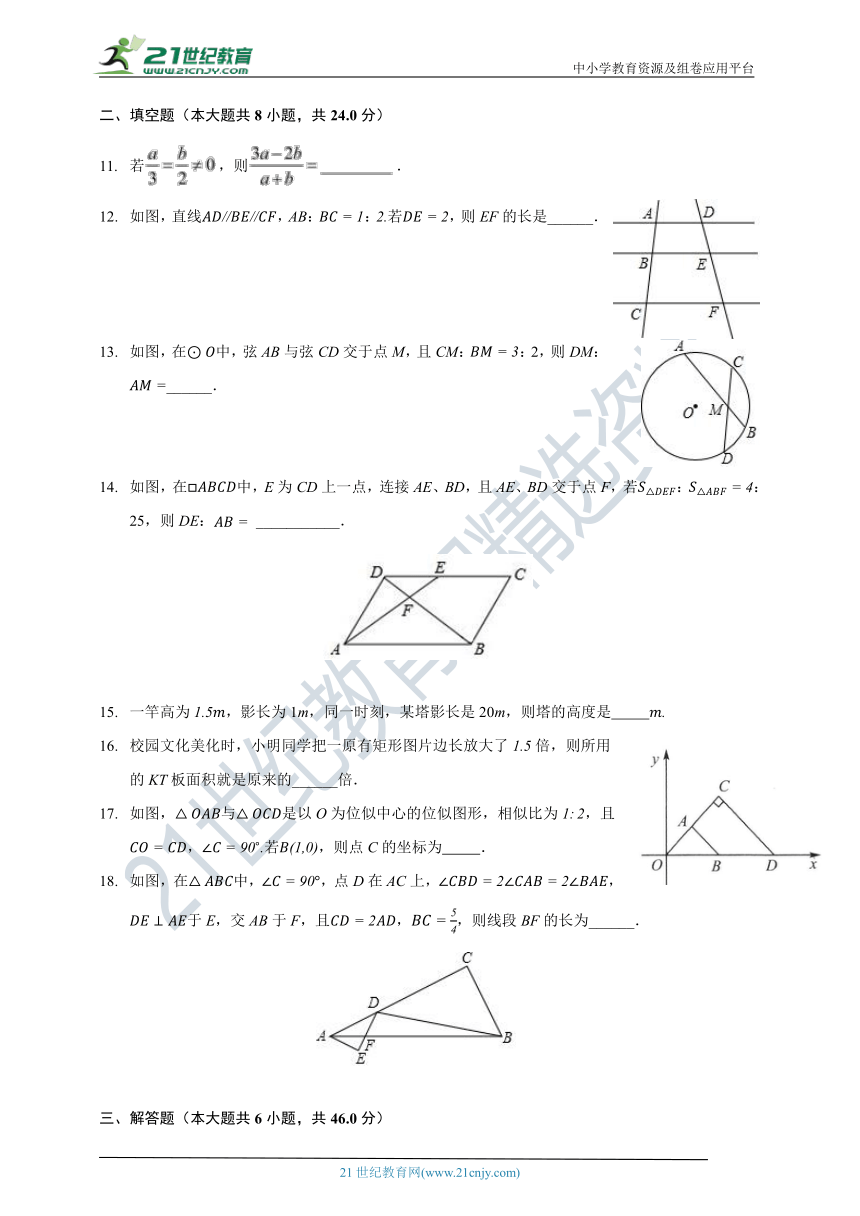
如图,直线,AB::若,则EF的长是______.
如图,在中,弦AB与弦CD交于点M,且CM::2,则DM:______.
如图,在中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若::25,则DE:___________.
一竿高为,影长为1m,同一时刻,某塔影长是20m,则塔的高度是??????????
校园文化美化时,小明同学把一原有矩形图片边长放大了倍,则所用的KT板面积就是原来的______倍.
如图,与是以O为位似中心的位似图形,相似比为,且,若,则点C的坐标为??????????.
如图,在中,,点D在AC上,,于E,交AB于F,且,,则线段BF的长为______.
三、解答题(本大题共6小题,共46.0分)
在一张比例尺为的设计图纸上有一个矩形花坛设计图,测得图纸上矩形花坛的长为12cm,宽为6cm.
设计图纸上矩形花坛的长与宽和花坛实际的长与宽是否成比例
求这个矩形花坛的实际长和宽.
如图所示,在中,点D是AB上的一点,过点D作交边AC于点E,过点E作交AD于点已知,求:
???
的值.
???
的值.
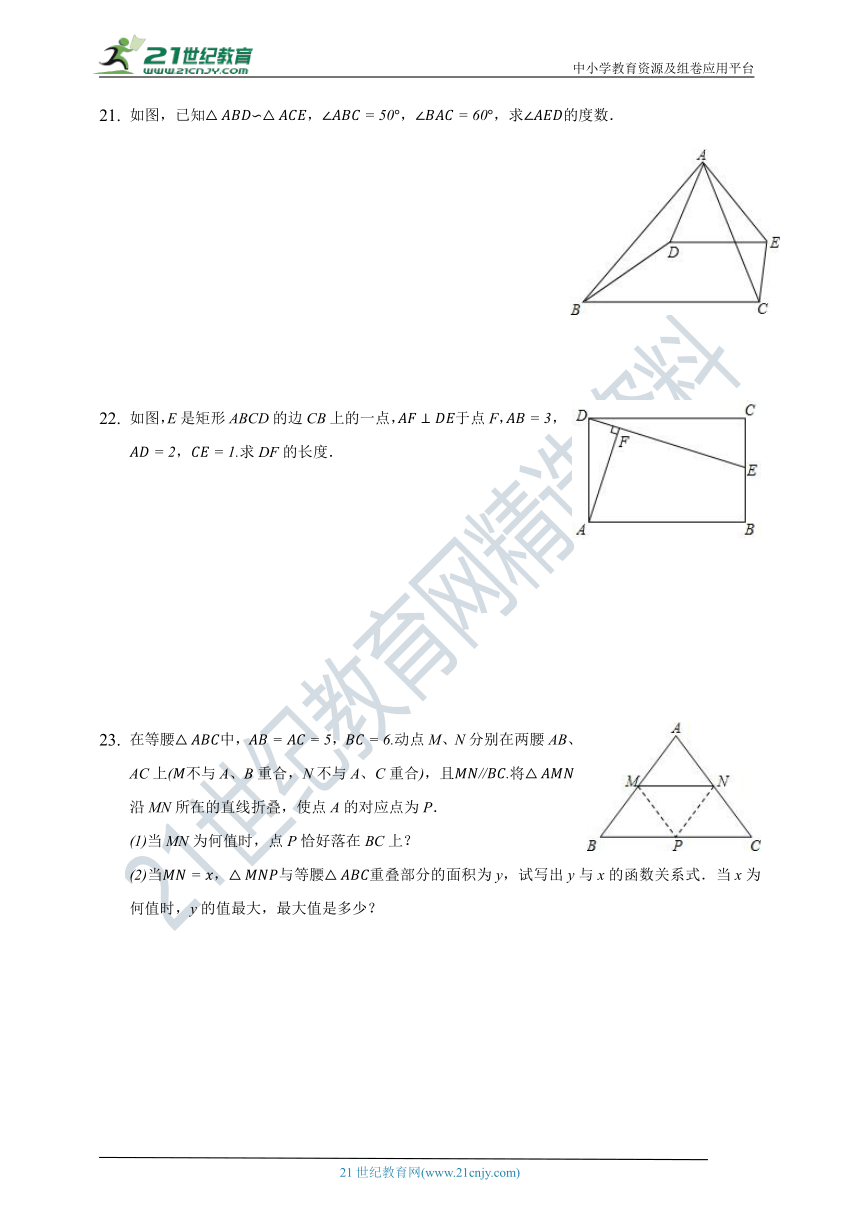
如图,已知∽,,,求的度数.
如图,E是矩形ABCD的边CB上的一点,于点F,,,求DF的长度.
在等腰中,,动点M、N分别在两腰AB、AC上不与A、B重合,N不与A、C重合,且将沿MN所在的直线折叠,使点A的对应点为P.
当MN为何值时,点P恰好落在BC上?
当,与等腰重叠部分的面积为y,试写出y与x的函数关系式.当x为何值时,y的值最大,最大值是多少?
以点,,为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.
直接写出E点坐标及直线AE的解析式;
求经过点O、D、C三点抛物线的解析式及顶点F的坐标;
一动点P从点A出发,沿射线AB以每秒一个单位长度的速度匀速运动.
?当t为何值时,直线PE把分成面积之比为1:3的两部分;
?在P点的运动过程中,是否存在某一时刻使为直角三角形?若存在,求出t的值;若不存在,请说明理由.
答案和解析
1.【答案】C
解:,
A.,所以16:14不能与14:16组成比例;
B.,所以13:12不能与14:16组成比例;
C.,所以7:8能与14:16组成比例;
D.,所以13:15不能与14:16组成比例.
故选C.
2.【答案】C
解:,,
,
,
:::5.
故选C.
3.【答案】C
解:∽,的周长为3,的周长为1,
三角形的相似比是3:1,
与的面积之比为9:1.
故选:C.
4.【答案】B
解:,,
,
又,
∽,
,
,
.
故选:B.
5.【答案】B
解:由题意知:光线AP与光线PC分别为入射光线和反射光线,,
∽,
,
米.
故选B.
6.【答案】A
解:四边形ABCD与四边形相似,
,,
∽,
.
故选A.
7.【答案】A
解:,位似比为1:2,
点E的对应点的坐标为或.
故选A.
8.【答案】C
解:如图,,,是等边三角形,
延长OA交地面于点,延长OB交地面于点,
可得OAB,则为等边三角形,
设光在该房间水平地面上形成的最大圆面的半径为r米,
则,解得,米,
根据等边三角形的性质知,点O到的距离为3米,
点O到此房间屋顶的距离约为米.
故选C.
9.【答案】D
解:设的面积为S,周长为C.
若,如图1,
则有∽,
;
若,如图2,
同理可得:;
若,如图3,
同理可得:.
,
,
,
.
故选D.
10.【答案】B
解:,
,,
是AB的中点,
点M的坐标为.
,,
,
,.
,
.
.
∽,故A选项不符合题意;
,即.
;故B选项符合题意;
,
不一定等于,
不一定与相似,故选项C不符合题意;
∽,
,故选项D不符合题意.
故选B.
11.【答案】1
解:,
,
.
故答案为1.
12.【答案】4
解:,
,即,
.
故答案为4.
13.【答案】2:3
解:连接AD、BC,如图所示.
,,
∽,
,
.
故答案为:2:3.
连接AD、BC,根据圆周角定理可得出、,进而可得出∽,根据相似三角形的性质可求出,此题得解.
本题考查了相似三角形的判定与性质以及圆周角定理,利用相似三角形的判定定理找出∽是解题的关键.
14.【答案】2:5
解:四边形ABCD为平行四边形,
,
∽,
::5,
故答案为2:5.
15.【答案】30
解:在同一时刻物高与影长成正比例
:塔的高度:20
塔的高度为30米.
故答案为:30.
16.【答案】
解:小明同学把一原有矩形图片边长放大了倍,
所用的KT板面积就是原来的:.
故答案为:.
直接利用相似多边形的性质分析得出答案.
此题主要考查了相似多边形的性质,正确把握相似多边形的面积比等于相似比的平方是解题关键.
17.【答案】
解:连接CB,
根据题意可得,,,等腰与等腰是位似图形,相似比为,
点B的坐标为,
,
,
?
,
,
故答案为.
18.【答案】
解:作交DE的延长线于H,ED的延长线交BC的延长线于作于R.
,
,,
,
,
,,
,
,,
,
,
,
,可以假设,
,,
∽,
,可得,
,
,
,
由∽,可得,
,,
,,,
,
,
,
,
在中,,
,
或舍弃,
,,
,
故答案为.
19.【答案】解:根据比例尺的定义可以得到设计图纸上矩形花坛的长与宽和花坛实际的长与宽是成比例;
设这个矩形花坛的实际长和宽分别为xcm,ycm.
由题意得
12::100,
解得:,
,
,
解得:,
则.
答:这个矩形花坛的实际长为12m,宽为6m.
20.【答案】解:,
,
,,
;
,
,
,
.
21.【答案】解:,,
,
∽,
,,
,,
,
∽,
,
.
22.【答案】解:四边形ABCD是矩形,
,.
,
.
,
,.
又,
,
∽,
,即,
,即DF的长度为.
23.【答案】解:连接AP,交MN于O,
将沿MN所在的直线折叠,使点A的对应点为P,
,,,,
,
∽,,
,
,
,
当时,点P恰好落在BC上;
过点A作于D,交MN于O,
,
,
∽,
,
,,,
,,
,
,
,
,
当时,
根据题意得:,
与等腰重叠部分的面积为,
,
当时,即时,y最大,最大值为3;
当时,
连接AP交MN于O,
则,
,
,∽,∽∽,
,,
即:,,
,
,
,,
,
当时,y有最大值,最大值为4,
综上所述:当时,y的值最大,最大值是4.
24.【答案】解:四边形OABC为矩形,是由沿AC翻折而成,且,,,则,
,,
≌,
,
设,则,
.
,
点为
设过A,E两点直线解析式为,则,
直线AE的解析式为:;
过D作于G,故∽,
,
,
,,即,,
,
由于过点O、D、C的抛物线经过原点,则设,而,,
,解之得,
,
,
故经点F的坐标为;
易求直线AC的解析式为,设直线PE交AC于H,,
过H作垂足为M,则∽,
,
::3或3:1,
:3或3:1即:4或3:4
或6,而或6,
,,
直线的解析式为,当时,;
直线的解析式为,当时,.
故当秒或15秒,直线EP把分成面积之比为1:3两部分.
当时,
,,
,即;
当时,
直线AE的解析式为:;
设直线PE的解析式为,
,
解得,
直线PE的解析式为,
当时,,
,即.
当秒或秒时,为直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
浙教版九年级数学上册单元测试卷
第4章
相似三角形
姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分)
与能组成比例的是
A.
?16:14
B.
13:12
C.
7:8
D.
13:15
如图,在中,,且,,则????
A.
B.
C.
D.
已知∽,的周长为3,的周长为1,则与的面积之比为
A.
3:1
B.
1:3
C.
9:1
D.
1:9
如图,在中,,且,,则BC等于
A.
10cm
B.
16cm
C.
12cm
D.
如图是小明测量某古城墙高度的示意图,点P处放一水平的平面镜,然后,后退至点B,从点A经平面镜刚好看到古城墙CD的顶端C处,已知,,且测得米,米,米,那么该古城墙的高度是
A.
6米
B.
8米
C.
18米
D.
24米
已知四边形ABCD∽四边形,四边形ABCD与四边形的周长分别为24,36,则它们对角线AC与的比为
A.
B.
C.
D.
直角坐标系中,,,以O为位似中心,按位似比为把缩小,则点E的对应点的坐标为?????
A.
或
B.
或
C.
D.
如图,在某圆锥形灯罩的轴截面中,,,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线在该房间水平地面上形成的最大圆面面积为平方米假设该水平地面足够大,则点O到此房间屋顶的距离约为
A.
米
B.
米
C.
米
D.
米
如图,已知?的三边长为a?,b?,c?,且?,若平行于三角形一边的直线l?将?的周长分成相等的两部分,设图中的小三角形、、的面积分别为,则的大小关系是???
.
A.
?
B.
C.
D.
如图,点A和点B都在坐标轴上,,M为AB的中点,,MP交y轴于点C,交x轴于点E,MQ交x轴于点D,交y轴于点F,在AB的左侧以M为中心旋转,设AD的长为,BC的长为n,则下列结论正确的是
A.
∽
B.
C.
∽
D.
二、填空题(本大题共8小题,共24.0分)
若,则.
如图,直线,AB::若,则EF的长是______.
如图,在中,弦AB与弦CD交于点M,且CM::2,则DM:______.
如图,在中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若::25,则DE:___________.
一竿高为,影长为1m,同一时刻,某塔影长是20m,则塔的高度是??????????
校园文化美化时,小明同学把一原有矩形图片边长放大了倍,则所用的KT板面积就是原来的______倍.
如图,与是以O为位似中心的位似图形,相似比为,且,若,则点C的坐标为??????????.
如图,在中,,点D在AC上,,于E,交AB于F,且,,则线段BF的长为______.
三、解答题(本大题共6小题,共46.0分)
在一张比例尺为的设计图纸上有一个矩形花坛设计图,测得图纸上矩形花坛的长为12cm,宽为6cm.
设计图纸上矩形花坛的长与宽和花坛实际的长与宽是否成比例
求这个矩形花坛的实际长和宽.
如图所示,在中,点D是AB上的一点,过点D作交边AC于点E,过点E作交AD于点已知,求:
???
的值.
???
的值.
如图,已知∽,,,求的度数.
如图,E是矩形ABCD的边CB上的一点,于点F,,,求DF的长度.
在等腰中,,动点M、N分别在两腰AB、AC上不与A、B重合,N不与A、C重合,且将沿MN所在的直线折叠,使点A的对应点为P.
当MN为何值时,点P恰好落在BC上?
当,与等腰重叠部分的面积为y,试写出y与x的函数关系式.当x为何值时,y的值最大,最大值是多少?
以点,,为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.
直接写出E点坐标及直线AE的解析式;
求经过点O、D、C三点抛物线的解析式及顶点F的坐标;
一动点P从点A出发,沿射线AB以每秒一个单位长度的速度匀速运动.
?当t为何值时,直线PE把分成面积之比为1:3的两部分;
?在P点的运动过程中,是否存在某一时刻使为直角三角形?若存在,求出t的值;若不存在,请说明理由.
答案和解析
1.【答案】C
解:,
A.,所以16:14不能与14:16组成比例;
B.,所以13:12不能与14:16组成比例;
C.,所以7:8能与14:16组成比例;
D.,所以13:15不能与14:16组成比例.
故选C.
2.【答案】C
解:,,
,
,
:::5.
故选C.
3.【答案】C
解:∽,的周长为3,的周长为1,
三角形的相似比是3:1,
与的面积之比为9:1.
故选:C.
4.【答案】B
解:,,
,
又,
∽,
,
,
.
故选:B.
5.【答案】B
解:由题意知:光线AP与光线PC分别为入射光线和反射光线,,
∽,
,
米.
故选B.
6.【答案】A
解:四边形ABCD与四边形相似,
,,
∽,
.
故选A.
7.【答案】A
解:,位似比为1:2,
点E的对应点的坐标为或.
故选A.
8.【答案】C
解:如图,,,是等边三角形,
延长OA交地面于点,延长OB交地面于点,
可得OAB,则为等边三角形,
设光在该房间水平地面上形成的最大圆面的半径为r米,
则,解得,米,
根据等边三角形的性质知,点O到的距离为3米,
点O到此房间屋顶的距离约为米.
故选C.
9.【答案】D
解:设的面积为S,周长为C.
若,如图1,
则有∽,
;
若,如图2,
同理可得:;
若,如图3,
同理可得:.
,
,
,
.
故选D.
10.【答案】B
解:,
,,
是AB的中点,
点M的坐标为.
,,
,
,.
,
.
.
∽,故A选项不符合题意;
,即.
;故B选项符合题意;
,
不一定等于,
不一定与相似,故选项C不符合题意;
∽,
,故选项D不符合题意.
故选B.
11.【答案】1
解:,
,
.
故答案为1.
12.【答案】4
解:,
,即,
.
故答案为4.
13.【答案】2:3
解:连接AD、BC,如图所示.
,,
∽,
,
.
故答案为:2:3.
连接AD、BC,根据圆周角定理可得出、,进而可得出∽,根据相似三角形的性质可求出,此题得解.
本题考查了相似三角形的判定与性质以及圆周角定理,利用相似三角形的判定定理找出∽是解题的关键.
14.【答案】2:5
解:四边形ABCD为平行四边形,
,
∽,
::5,
故答案为2:5.
15.【答案】30
解:在同一时刻物高与影长成正比例
:塔的高度:20
塔的高度为30米.
故答案为:30.
16.【答案】
解:小明同学把一原有矩形图片边长放大了倍,
所用的KT板面积就是原来的:.
故答案为:.
直接利用相似多边形的性质分析得出答案.
此题主要考查了相似多边形的性质,正确把握相似多边形的面积比等于相似比的平方是解题关键.
17.【答案】
解:连接CB,
根据题意可得,,,等腰与等腰是位似图形,相似比为,
点B的坐标为,
,
,
?
,
,
故答案为.
18.【答案】
解:作交DE的延长线于H,ED的延长线交BC的延长线于作于R.
,
,,
,
,
,,
,
,,
,
,
,
,可以假设,
,,
∽,
,可得,
,
,
,
由∽,可得,
,,
,,,
,
,
,
,
在中,,
,
或舍弃,
,,
,
故答案为.
19.【答案】解:根据比例尺的定义可以得到设计图纸上矩形花坛的长与宽和花坛实际的长与宽是成比例;
设这个矩形花坛的实际长和宽分别为xcm,ycm.
由题意得
12::100,
解得:,
,
,
解得:,
则.
答:这个矩形花坛的实际长为12m,宽为6m.
20.【答案】解:,
,
,,
;
,
,
,
.
21.【答案】解:,,
,
∽,
,,
,,
,
∽,
,
.
22.【答案】解:四边形ABCD是矩形,
,.
,
.
,
,.
又,
,
∽,
,即,
,即DF的长度为.
23.【答案】解:连接AP,交MN于O,
将沿MN所在的直线折叠,使点A的对应点为P,
,,,,
,
∽,,
,
,
,
当时,点P恰好落在BC上;
过点A作于D,交MN于O,
,
,
∽,
,
,,,
,,
,
,
,
,
当时,
根据题意得:,
与等腰重叠部分的面积为,
,
当时,即时,y最大,最大值为3;
当时,
连接AP交MN于O,
则,
,
,∽,∽∽,
,,
即:,,
,
,
,,
,
当时,y有最大值,最大值为4,
综上所述:当时,y的值最大,最大值是4.
24.【答案】解:四边形OABC为矩形,是由沿AC翻折而成,且,,,则,
,,
≌,
,
设,则,
.
,
点为
设过A,E两点直线解析式为,则,
直线AE的解析式为:;
过D作于G,故∽,
,
,
,,即,,
,
由于过点O、D、C的抛物线经过原点,则设,而,,
,解之得,
,
,
故经点F的坐标为;
易求直线AC的解析式为,设直线PE交AC于H,,
过H作垂足为M,则∽,
,
::3或3:1,
:3或3:1即:4或3:4
或6,而或6,
,,
直线的解析式为,当时,;
直线的解析式为,当时,.
故当秒或15秒,直线EP把分成面积之比为1:3两部分.
当时,
,,
,即;
当时,
直线AE的解析式为:;
设直线PE的解析式为,
,
解得,
直线PE的解析式为,
当时,,
,即.
当秒或秒时,为直角三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
