第3章 圆的基本性质单元测试卷(含解析)
文档属性
| 名称 | 第3章 圆的基本性质单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-11 16:38:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级数学上册单元测试卷
第3章
圆的基本性质
姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分)
已知的半径是4,点P到圆心的距离,则点P与的位置关系是
A.
点P在圆上
B.
点P在圆外
C.
点P在圆内
D.
无法确定
如图,,O是AB上一点,直线OD与AB所夹的,要使,直线OD绕点O按逆时针方向至少旋转
A.
B.
C.
D.
如图,已知的直径于点E,则下列结论可能错误的是.
A.
B.
C.
弧弧BD
D.
≌
如图所示,在中,,,以点C为圆心,BC为半径的圆分别交AB,AC于点D,E,则的度数为?
???
A.
B.
C.
D.
如图,点A,B,C都在上,且点C在弦AB所对的优弧上,若,则的度数是?
?
?
A.
B.
C.
D.
如图,四边形ABCD内接于,,则
A.
B.
C.
D.
古代数学家祖冲之和他的儿子根据刘徽的“割圆术”用圆内接正多边形的周长代替圆周长,来计算圆周率的近似值.他从正六边形算起,一直算到正24576边形,将圆周率精确到小数后七位,在世界上领先一千多年.根据这个办法,由圆内接正六边形算得的圆周率的近似值是
A.
B.
3
C.
D.
在矩形ABCD中,已知,,现有一根长为2cm的木棒EF紧贴着矩形的边即两个端点始终落在矩形的边上,按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为
A.
B.
C.
D.
如图,在三个等圆上各有一条劣弧,弧AB、弧CD、弧EF,如果,那么与EF的大小关系是???
???
A.
B.
C.
D.
大小关系不确定
设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为?
?
A.
3
B.
2
C.
4或10
D.
2或5
二、填空题(本大题共8小题,共24.0分)
已知的半径是2,如果B是外一点,那么线段AB长度的取值范围是??????????.
把一个正六边形绕着其对称中心旋转一定的角度,要使旋转后的图形与原来的图形重合,那么旋转的角度至少是______
如图,AB为的弦,P为AB上一点,且,,,则的半径为______.
如图,AD为的直径,A,B,C三点在上,,BD交AC于点E,,则为______
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且,,则______.
正n边形的一个外角为,外接圆半径为4,则它的边长为______.
在中,,,则这个三角形的外接圆的直径是?
?
?
?
?
?
?
?
?。
如图,A、B、C是上的三点,以BC为一边,作,过BC上一点P,作交BD于点若,,则点P到弦AB的距离为???????????.
三、解答题(本大题共6小题,共46.0分)
在矩形ABCD中,,,现以点A为圆心画圆,使B,C,D三点至少有一个点在圆内,且至少有一点在圆外,试确定的半径r的取值范围.
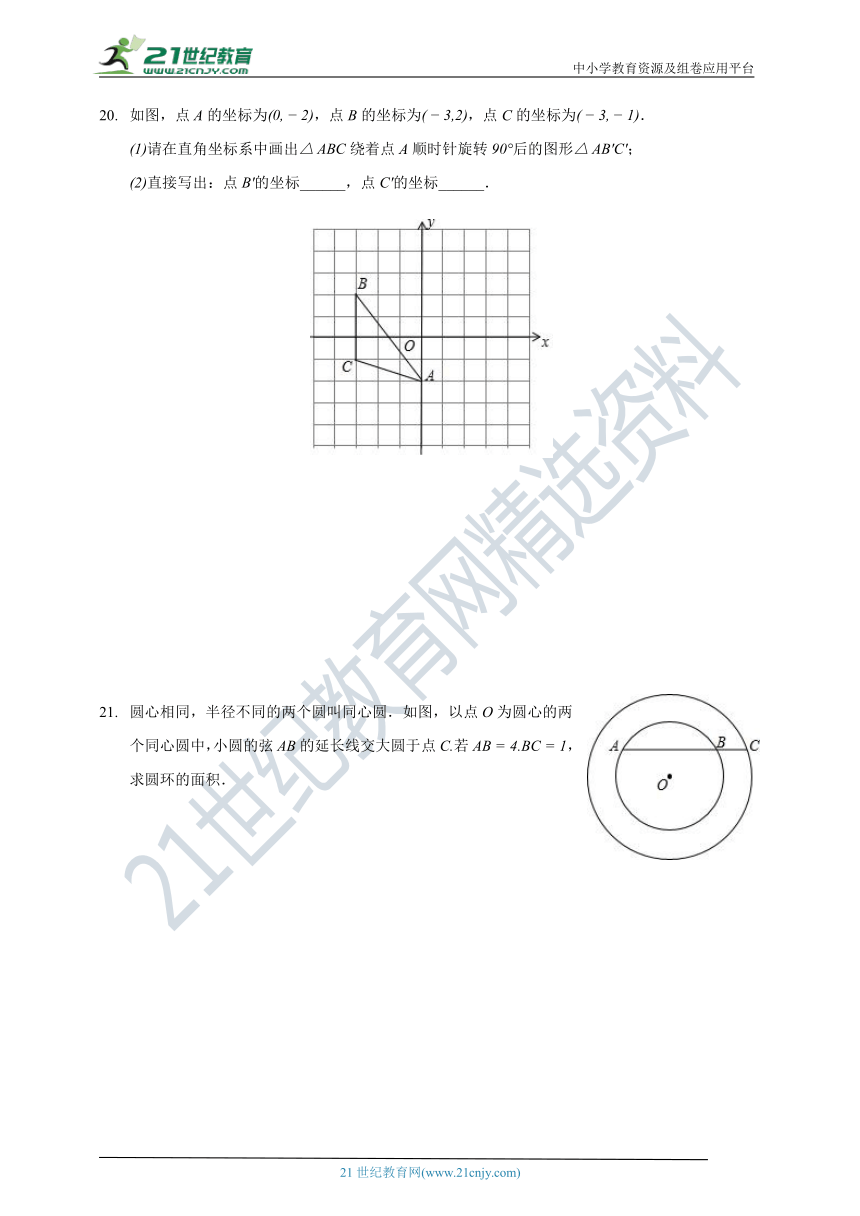
如图,点A的坐标为,点B的坐标为,点C的坐标为.
请在直角坐标系中画出绕着点A顺时针旋转后的图形;
直接写出:点的坐标______,点的坐标______.
圆心相同,半径不同的两个圆叫同心圆.如图,以点O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点若,求圆环的面积.
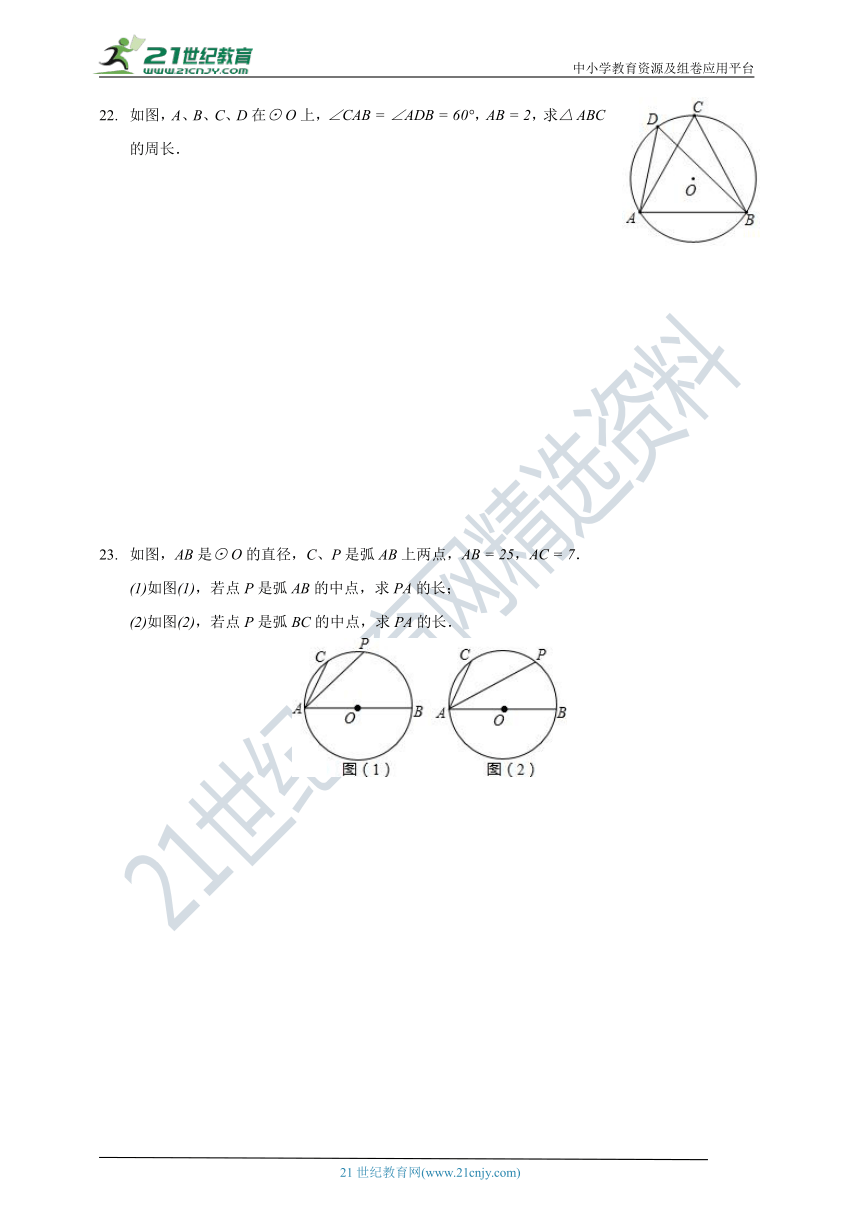
如图,A、B、C、D在上,,,求的周长.
如图,AB是的直径,C、P是弧AB上两点,,.
如图,若点P是弧AB的中点,求PA的长;
如图,若点P是弧BC的中点,求PA的长.
把一副三角板如图1放置,其中,,,斜边,,把三角板DCE绕点C顺时针旋转得到如图,这时AB与交于点O,与相交于点F.
求的度数;
求线段的长
若把三角形绕着点C顺时针再旋转得,这时点B在的内部、外部、还是边上?
答案和解析
1.【答案】C
解:的半径为4,点P到圆心的距离,?
,?
点P与的位置关系是:点P在圆内,?
故选C.
2.【答案】D
解:,
,
,
故选D.
3.【答案】B
解:的直径于点E
,
,,
在和中,
,
,
选项A
、C
、D
正确,不符合题意;选项B
不正确,符合题意.
故选B
.
4.【答案】C
解:,,
,
,
,
,
的度数为.
故选C.
5.【答案】C
解:.
故选C.
6.【答案】C
解:,
.
.
故选C.
7.【答案】B
解:由题意时,,
故选:B.
8.【答案】D
解:如图所示:由题意根据直角三角形斜边上的中线等于斜边的一半,得出P到B点距离始终为1,
则木棒EF的中点P在运动过程中的轨迹为分别以A,B,C,D为圆心,1cm为半径的弧,
故所围成的图形的面积为:矩形面积个扇形面积
故选:D.
9.【答案】C
解:如图,在上取一点M使,
则,
,,
在中,,
.
故选:C.
10.【答案】B
解:为外一点,若点P到的最短距离为3,最长距离为7,
的直径为:,
的半径为2,
故选B.
11.【答案】
略
12.【答案】60
解:正六边形旋转最小的角度,,
故答案为:
13.【答案】8
解:过O作,垂足为E,连接OA,
,,
,,
在中,,
在中,,
故答案为:8.
14.【答案】20
解:为的直径,
,
,
.
.
故答案为20.
15.【答案】
解:四边形ABCD是圆内接四边形,
,
是的一个外角,
,
,
故答案为.
16.【答案】4
解:正n边形的一个外角为,
,
正六边形的外接圆半径与边长相等,
正六边形的边长为4.
故答案为:4.
17.【答案】8或10
解:根据题意得
斜边是BC,即外接圆直径是8;
?斜边是AC,即外接圆直径是;
故答案为8或10.
18.【答案】
解:此题比较复杂,考查圆周角定理及角平分线的性质.
过P作,
,交BD于点E,,
为的角平分线,
又
即
,
则点P到弦AB的距离为,
故答案为:.
19.【答案】解:如图,
在矩形ABCD中,,,
,
以点A为圆心画圆,使B,C,D三点至少有一个点在圆内,且至少有一点在圆外,
圆的半径r满足.
20.【答案】?
解:如图,为所作;
点的坐标为,点的坐标为.
故答案为,.
利用网格特点和旋转的性质画出B、C点的对应点、即可;
利用所画图形写出点的坐标,点的坐标.
本题考查了作图旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
21.【答案】解:如图,过点O作,垂足为D,
,,
,,
.
22.【答案】解:,
而,
是等边三角形,
的周长.
23.【答案】解:如图所示,连接PB,
是的直径且P是的中点,
,,
又在等腰三角形中有,
;
如图所示:连接相交于M点,作于点N,
点为弧BC的中点,
,,
又因为AB为直径,
,
,
,
,
又因为,
∽
,
又,,,
代入得,
,
在中,有
在中有
.
24.【答案】解:如图所示,,,
,
又,
;
,
,
,
,
又,
即是等腰直角三角形.
,
,
,
又,
,
在中,;
点B在内部,
理由如下:设或延长线交于点P
则,
在中,,
,即,
点B在内部.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
浙教版九年级数学上册单元测试卷
第3章
圆的基本性质
姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30.0分)
已知的半径是4,点P到圆心的距离,则点P与的位置关系是
A.
点P在圆上
B.
点P在圆外
C.
点P在圆内
D.
无法确定
如图,,O是AB上一点,直线OD与AB所夹的,要使,直线OD绕点O按逆时针方向至少旋转
A.
B.
C.
D.
如图,已知的直径于点E,则下列结论可能错误的是.
A.
B.
C.
弧弧BD
D.
≌
如图所示,在中,,,以点C为圆心,BC为半径的圆分别交AB,AC于点D,E,则的度数为?
???
A.
B.
C.
D.
如图,点A,B,C都在上,且点C在弦AB所对的优弧上,若,则的度数是?
?
?
A.
B.
C.
D.
如图,四边形ABCD内接于,,则
A.
B.
C.
D.
古代数学家祖冲之和他的儿子根据刘徽的“割圆术”用圆内接正多边形的周长代替圆周长,来计算圆周率的近似值.他从正六边形算起,一直算到正24576边形,将圆周率精确到小数后七位,在世界上领先一千多年.根据这个办法,由圆内接正六边形算得的圆周率的近似值是
A.
B.
3
C.
D.
在矩形ABCD中,已知,,现有一根长为2cm的木棒EF紧贴着矩形的边即两个端点始终落在矩形的边上,按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为
A.
B.
C.
D.
如图,在三个等圆上各有一条劣弧,弧AB、弧CD、弧EF,如果,那么与EF的大小关系是???
???
A.
B.
C.
D.
大小关系不确定
设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为?
?
A.
3
B.
2
C.
4或10
D.
2或5
二、填空题(本大题共8小题,共24.0分)
已知的半径是2,如果B是外一点,那么线段AB长度的取值范围是??????????.
把一个正六边形绕着其对称中心旋转一定的角度,要使旋转后的图形与原来的图形重合,那么旋转的角度至少是______
如图,AB为的弦,P为AB上一点,且,,,则的半径为______.
如图,AD为的直径,A,B,C三点在上,,BD交AC于点E,,则为______
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且,,则______.
正n边形的一个外角为,外接圆半径为4,则它的边长为______.
在中,,,则这个三角形的外接圆的直径是?
?
?
?
?
?
?
?
?。
如图,A、B、C是上的三点,以BC为一边,作,过BC上一点P,作交BD于点若,,则点P到弦AB的距离为???????????.
三、解答题(本大题共6小题,共46.0分)
在矩形ABCD中,,,现以点A为圆心画圆,使B,C,D三点至少有一个点在圆内,且至少有一点在圆外,试确定的半径r的取值范围.
如图,点A的坐标为,点B的坐标为,点C的坐标为.
请在直角坐标系中画出绕着点A顺时针旋转后的图形;
直接写出:点的坐标______,点的坐标______.
圆心相同,半径不同的两个圆叫同心圆.如图,以点O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点若,求圆环的面积.
如图,A、B、C、D在上,,,求的周长.
如图,AB是的直径,C、P是弧AB上两点,,.
如图,若点P是弧AB的中点,求PA的长;
如图,若点P是弧BC的中点,求PA的长.
把一副三角板如图1放置,其中,,,斜边,,把三角板DCE绕点C顺时针旋转得到如图,这时AB与交于点O,与相交于点F.
求的度数;
求线段的长
若把三角形绕着点C顺时针再旋转得,这时点B在的内部、外部、还是边上?
答案和解析
1.【答案】C
解:的半径为4,点P到圆心的距离,?
,?
点P与的位置关系是:点P在圆内,?
故选C.
2.【答案】D
解:,
,
,
故选D.
3.【答案】B
解:的直径于点E
,
,,
在和中,
,
,
选项A
、C
、D
正确,不符合题意;选项B
不正确,符合题意.
故选B
.
4.【答案】C
解:,,
,
,
,
,
的度数为.
故选C.
5.【答案】C
解:.
故选C.
6.【答案】C
解:,
.
.
故选C.
7.【答案】B
解:由题意时,,
故选:B.
8.【答案】D
解:如图所示:由题意根据直角三角形斜边上的中线等于斜边的一半,得出P到B点距离始终为1,
则木棒EF的中点P在运动过程中的轨迹为分别以A,B,C,D为圆心,1cm为半径的弧,
故所围成的图形的面积为:矩形面积个扇形面积
故选:D.
9.【答案】C
解:如图,在上取一点M使,
则,
,,
在中,,
.
故选:C.
10.【答案】B
解:为外一点,若点P到的最短距离为3,最长距离为7,
的直径为:,
的半径为2,
故选B.
11.【答案】
略
12.【答案】60
解:正六边形旋转最小的角度,,
故答案为:
13.【答案】8
解:过O作,垂足为E,连接OA,
,,
,,
在中,,
在中,,
故答案为:8.
14.【答案】20
解:为的直径,
,
,
.
.
故答案为20.
15.【答案】
解:四边形ABCD是圆内接四边形,
,
是的一个外角,
,
,
故答案为.
16.【答案】4
解:正n边形的一个外角为,
,
正六边形的外接圆半径与边长相等,
正六边形的边长为4.
故答案为:4.
17.【答案】8或10
解:根据题意得
斜边是BC,即外接圆直径是8;
?斜边是AC,即外接圆直径是;
故答案为8或10.
18.【答案】
解:此题比较复杂,考查圆周角定理及角平分线的性质.
过P作,
,交BD于点E,,
为的角平分线,
又
即
,
则点P到弦AB的距离为,
故答案为:.
19.【答案】解:如图,
在矩形ABCD中,,,
,
以点A为圆心画圆,使B,C,D三点至少有一个点在圆内,且至少有一点在圆外,
圆的半径r满足.
20.【答案】?
解:如图,为所作;
点的坐标为,点的坐标为.
故答案为,.
利用网格特点和旋转的性质画出B、C点的对应点、即可;
利用所画图形写出点的坐标,点的坐标.
本题考查了作图旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
21.【答案】解:如图,过点O作,垂足为D,
,,
,,
.
22.【答案】解:,
而,
是等边三角形,
的周长.
23.【答案】解:如图所示,连接PB,
是的直径且P是的中点,
,,
又在等腰三角形中有,
;
如图所示:连接相交于M点,作于点N,
点为弧BC的中点,
,,
又因为AB为直径,
,
,
,
,
又因为,
∽
,
又,,,
代入得,
,
在中,有
在中有
.
24.【答案】解:如图所示,,,
,
又,
;
,
,
,
,
又,
即是等腰直角三角形.
,
,
,
又,
,
在中,;
点B在内部,
理由如下:设或延长线交于点P
则,
在中,,
,即,
点B在内部.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
