浙教版九年级数学上册 3.6-圆内接四边形课件(共19张PPT)
文档属性
| 名称 | 浙教版九年级数学上册 3.6-圆内接四边形课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
3.6圆内接四边形
复习提问:
1、圆周角定理的内容是怎样叙述的?
答:一条弧所对的圆周角等于它所对的圆心角的一半。
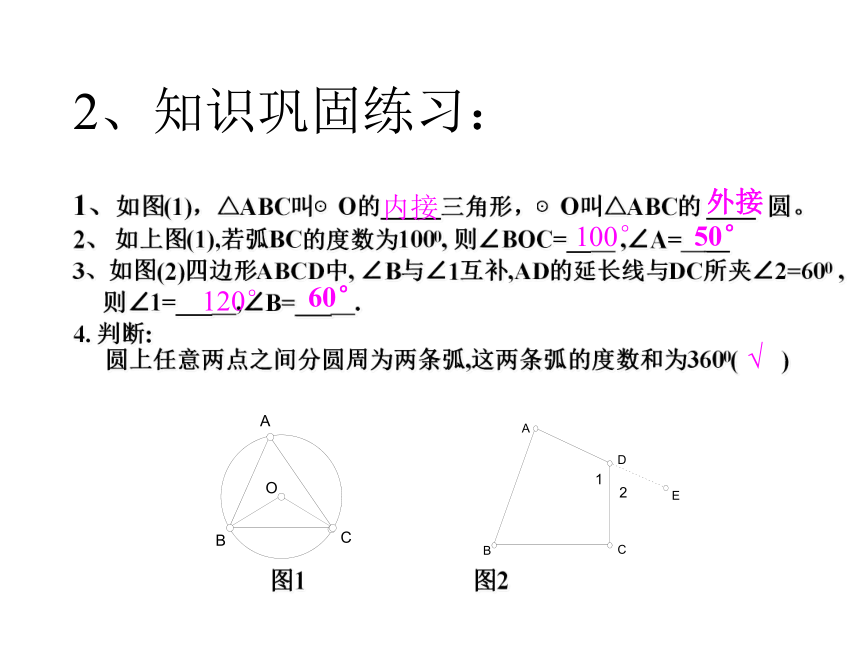
2、知识巩固练习:
1、如图(1),△ABC叫⊙O的_____三角形,⊙O叫△ABC的
____
圆。
2、
如上图(1),若弧BC的度数为1000,
则∠BOC=__
,∠A=
__
3、如图(2)四边形ABCD中,
∠B与∠1互补,AD的延长线与DC所夹∠2=600
,
则∠1=___
,∠B=___
.
4.
判断:
圆上任意两点之间分圆周为两条弧,这两条弧的度数和为3600(
)
图1
图2
内接
外接
100°
50°
120°
60°
√
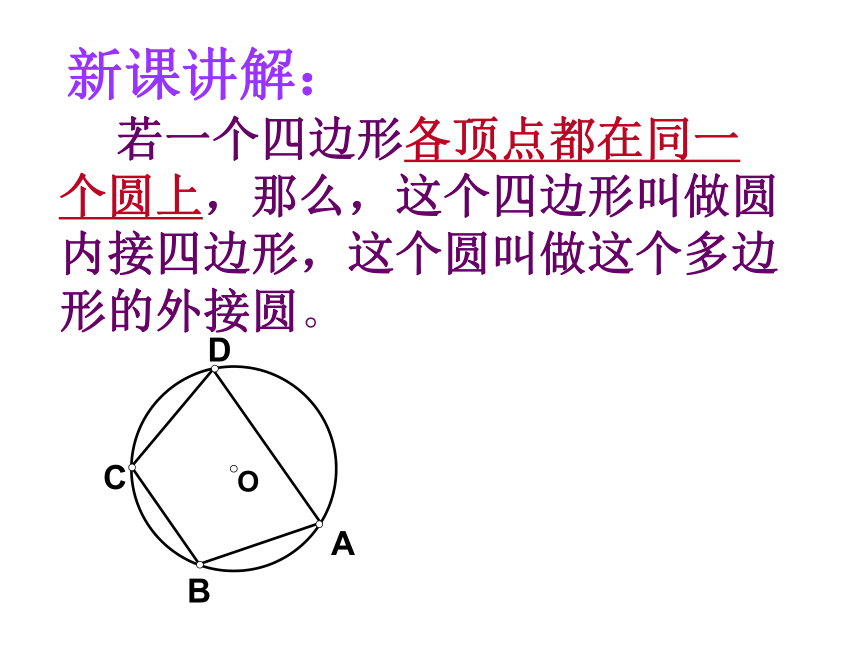
新课讲解:
若一个四边形各顶点都在同一个圆上,那么,这个四边形叫做圆内接四边形,这个圆叫做这个多边形的外接圆。
O
A
C
D
B
O
C
A
B
D
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
思考:∠A与∠C有什么关系?∠B与∠D有什么关系?
C
O
D
B
A
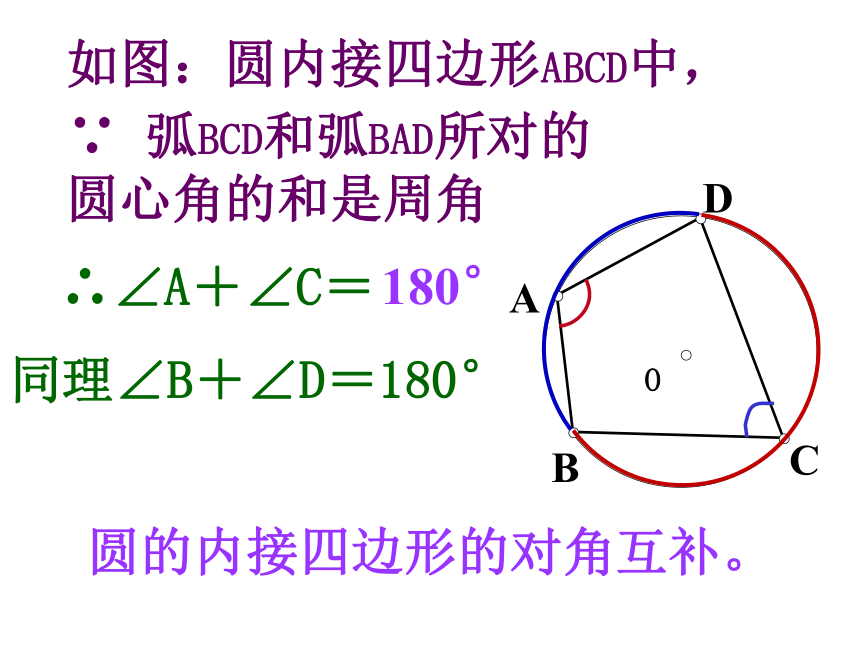
如图:圆内接四边形ABCD中,
∵
弧BCD和弧BAD所对的圆心角的和是周角
∴∠A+∠C=
180°
同理∠B+∠D=180°
圆的内接四边形的对角互补。
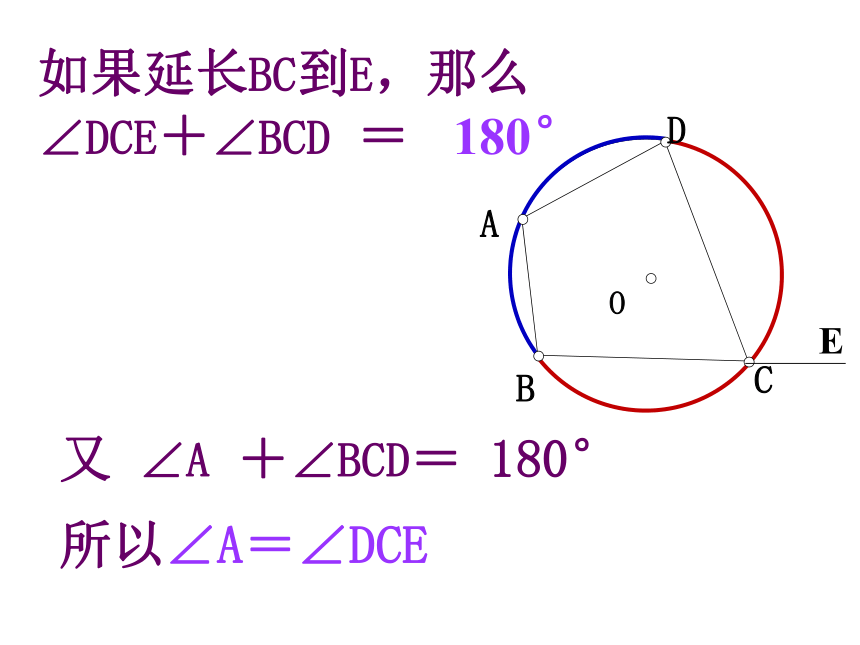
如果延长BC到E,那么∠DCE+∠BCD
=
180°
所以∠A=∠DCE
又
∠A
+∠BCD=
180°
C
O
D
B
A
E
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。
圆内接四边形的一个
外角等于它的内对角。
C
O
D
B
A
E
C
O
D
B
A
E
1
2
3
4
5
6
7
定理:
圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
要会用到解题中
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
几何表达式:
∵ ABCD是⊙O的内接四边形,
∴
∠A+∠C=180°
且∠B=∠1
巩固练习:
1、如图,四边形ABCD为⊙O
的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。
A
O
D
B
C
2.求证:圆内接平行四边形是矩形。
O
C
D
B
A
3.已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。
求证:四边形ABCD
是矩形。
(1)如图5,四边形ABCD内接于⊙O,则∠A+∠C=__
,∠B+∠ADC=_____;若∠B=800,
则∠ADC=______
∠CDE=______
(2)如图6,四边形ABCD内接于⊙O,∠AOC=1000
则∠B=______∠D=______
(3)四边形ABCD内接于⊙O,
∠A:∠C=1:3,则∠A=_____,
180°
180°
100°
80°
?
50°
130°
45°
4.填空
图5
图6)
(
(4)梯形ABCD内接于⊙O,AD∥BC,
∠B=750,则∠C=_____
75°
圆的内接梯形一定是_____梯形。
等
腰
若ABCD为圆内接四边形,则下列哪个选项可能成立(
)
(A)∠A∶∠B∶∠C∶∠D
=
1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D
=
2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D
=
3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D
=
4∶3∶2∶1
B
补充练习:
再见!
再见!
再见!
再见!
再见!
再见!
再见!
再见!
3.6圆内接四边形
复习提问:
1、圆周角定理的内容是怎样叙述的?
答:一条弧所对的圆周角等于它所对的圆心角的一半。
2、知识巩固练习:
1、如图(1),△ABC叫⊙O的_____三角形,⊙O叫△ABC的
____
圆。
2、
如上图(1),若弧BC的度数为1000,
则∠BOC=__
,∠A=
__
3、如图(2)四边形ABCD中,
∠B与∠1互补,AD的延长线与DC所夹∠2=600
,
则∠1=___
,∠B=___
.
4.
判断:
圆上任意两点之间分圆周为两条弧,这两条弧的度数和为3600(
)
图1
图2
内接
外接
100°
50°
120°
60°
√
新课讲解:
若一个四边形各顶点都在同一个圆上,那么,这个四边形叫做圆内接四边形,这个圆叫做这个多边形的外接圆。
O
A
C
D
B
O
C
A
B
D
如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。
思考:∠A与∠C有什么关系?∠B与∠D有什么关系?
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵
弧BCD和弧BAD所对的圆心角的和是周角
∴∠A+∠C=
180°
同理∠B+∠D=180°
圆的内接四边形的对角互补。
如果延长BC到E,那么∠DCE+∠BCD
=
180°
所以∠A=∠DCE
又
∠A
+∠BCD=
180°
C
O
D
B
A
E
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。
圆内接四边形的一个
外角等于它的内对角。
C
O
D
B
A
E
C
O
D
B
A
E
1
2
3
4
5
6
7
定理:
圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
要会用到解题中
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
几何表达式:
∵ ABCD是⊙O的内接四边形,
∴
∠A+∠C=180°
且∠B=∠1
巩固练习:
1、如图,四边形ABCD为⊙O
的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。
A
O
D
B
C
2.求证:圆内接平行四边形是矩形。
O
C
D
B
A
3.已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。
求证:四边形ABCD
是矩形。
(1)如图5,四边形ABCD内接于⊙O,则∠A+∠C=__
,∠B+∠ADC=_____;若∠B=800,
则∠ADC=______
∠CDE=______
(2)如图6,四边形ABCD内接于⊙O,∠AOC=1000
则∠B=______∠D=______
(3)四边形ABCD内接于⊙O,
∠A:∠C=1:3,则∠A=_____,
180°
180°
100°
80°
?
50°
130°
45°
4.填空
图5
图6)
(
(4)梯形ABCD内接于⊙O,AD∥BC,
∠B=750,则∠C=_____
75°
圆的内接梯形一定是_____梯形。
等
腰
若ABCD为圆内接四边形,则下列哪个选项可能成立(
)
(A)∠A∶∠B∶∠C∶∠D
=
1∶2∶3∶4
(B)∠A∶∠B∶∠C∶∠D
=
2∶1∶3∶4
(C)∠A∶∠B∶∠C∶∠D
=
3∶2∶1∶4
(D)∠A∶∠B∶∠C∶∠D
=
4∶3∶2∶1
B
补充练习:
再见!
再见!
再见!
再见!
再见!
再见!
再见!
再见!
同课章节目录
