浙教版九年级数学上册单元测试卷附答案:第4章 相似三角形(Word版)
文档属性
| 名称 | 浙教版九年级数学上册单元测试卷附答案:第4章 相似三角形(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 11:35:02 | ||
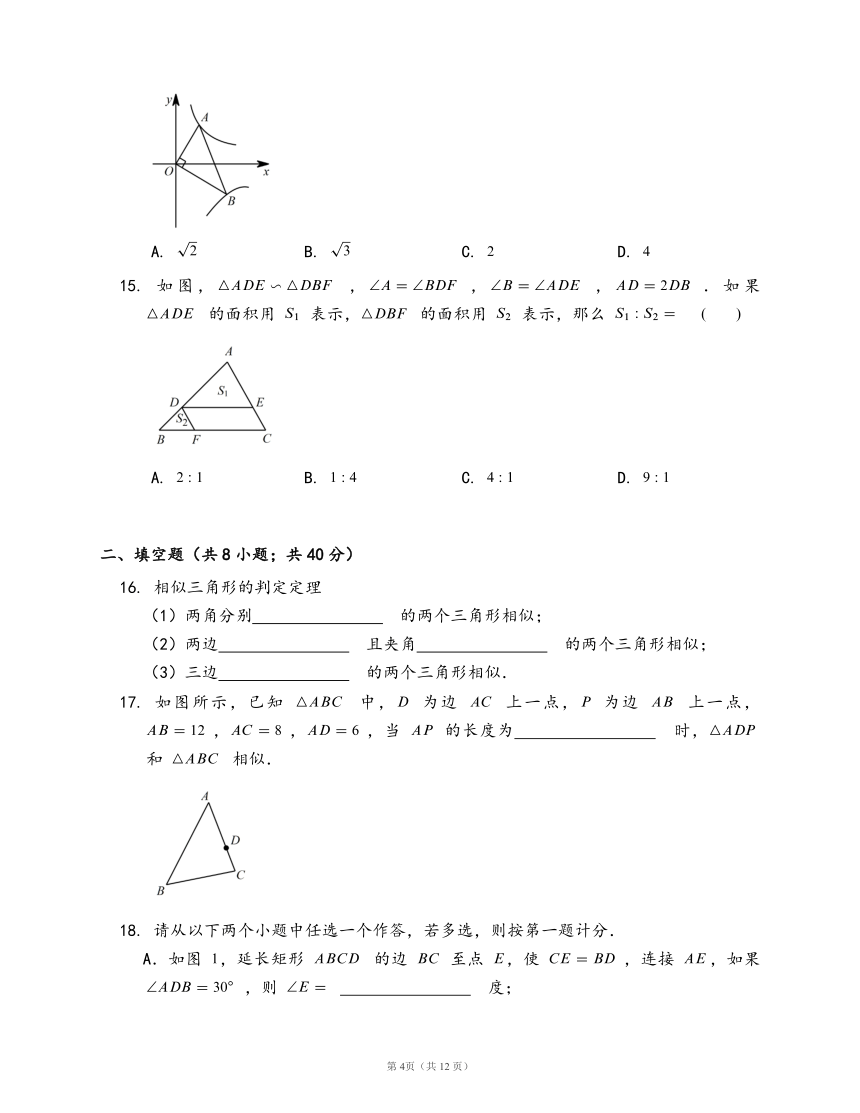
图片预览




文档简介
第4章
相似三角形
一、选择题(共15小题;共45分)
1.
下列各组图形一定相似的是
A.
两个菱形
B.
两个矩形
C.
两个直角梯形
D.
两个正方形
2.
如图,在
中,,,,,则
的长为
A.
B.
C.
D.
3.
如果
,那么
A.
B.
C.
D.
4.
如图,小正方形的边长均为
,则图中三角形(阴影部分)与
相似的是
A.
B.
C.
D.
5.
已知
,五边形
的最短边为
,最长边为
,五边形
的最长边是
,则五边形
的最短边是
A.
B.
C.
D.
6.
如图,在
中,点
,
分别在边
,
上,若
,则
A.
B.
C.
D.
7.
已知两点
,,先将线段
向左平移一个单位,再以原点
为位似中心,在第一象限内将其缩小为原来的
得到线段
,则点
的对应点
的坐标为
A.
B.
C.
D.
8.
如图,,,,,,,,,
都是方格纸中的格点(即小正方形的顶点),要使
与
相似,则点
应是
,,,
四点中的
A.
或
B.
或
C.
或
D.
或
9.
下列结论中,不正确的是
A.
有一个角相等,两条边对应成比例的两个三角形相似
B.
顺次连接三角形各边中点所得的三角形与原三角形相似
C.
如果三角形两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似
D.
钝角相等的两个等腰三角形相似
10.
应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的"大唐芙蓉园".该园占地面积约为
,若按比例尺
缩小后,其面积大约相当于
A.
一个篮球场的面积
B.
一张乒乓球台台面的面积
C.
《陕西日报》的一个版面的面积
D.
《数学》课本封面的面积
11.
若一个三角形各边的长度都扩大到原来的
倍,则扩大后的三角形各角的度数都
A.
缩小到原来的
B.
不变
C.
扩大到原来的
倍
D.
扩大到原来的
倍
12.
已知菱形
,,
是动点,边长为
,,,若
,则
A.
B.
C.
D.
13.
中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离
的示意图中,记照板“内芯”的高度为
,观测者的眼睛(图中用点
表示)与
,
在同一水平线上,则下列结论中,正确的是
A.
B.
C.
D.
14.
如图,已知点
,
分别在反比例函数
,
的图象上,且
,则
的值为
A.
B.
C.
D.
15.
如图,,,,.如果
的面积用
表示,
的面积用
表示,那么
A.
B.
C.
D.
二、填空题(共8小题;共40分)
16.
相似三角形的判定定理
(1)两角分别
?
的两个三角形相似;
(2)两边
?
且夹角
?
的两个三角形相似;
(3)三边
?
的两个三角形相似.
17.
如图所示,已知
中,
为边
上一点,
为边
上一点,,,,当
的长度为
?
时,
和
相似.
18.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.如图
,延长矩形
的边
至点
,使
,连接
,如果
,则
?
度;
B.如图
,,,,,则
?,
?.
19.
如图,已知
,且相似比是
,已知
,则
?.
20.
已知
,,
是
,
的比例中项,则
?.
21.
一个三角形的三边之比为
,另一个三角形的最短边长为
,另外两边长为
?时,这两个三角形相似.
22.
如图,线段
两个端点的坐标分别为
,.以原点
为位似中心,在第一象限内将线段
缩小为原来的
后得到线段
,则端点
的坐标为
?.
23.
如图,已知第一象限内的点
在反比例函数
的图象上,第二象限内的点
在反比例函数
的图象上,且
,,则
的面积为
?.
三、解答题(共5小题;共65分)
24.
周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点
,在他们所在的岸边选择了点
,使得
与河岸垂直,并在
点竖起标杆
,再在
的延长线上选择点
竖起标杆
,使得点
与点
,
共线.
已知:,,测得
,,.测量示意图如图所示.请根据相关测量信息,求河宽
.
25.
如图,将一张长宽之比为
的矩形纸片
依次不断对折,可以得到矩形
,矩形
,矩形
,矩形
.
(1)在折叠过程中,这些矩形的长和宽的比变了吗?请说明理由;
(2)在这些矩形中,有成比例的线段吗?
26.
如图,两条直线
,
被三条平行线
,,
所截,且
,,求
的长.
27.
已知:如图,在正方形
中,
是
上的点,且
,
是
的中点.求证:.
28.
如图,正三角形
的边长为
.
(1)如图
1,正方形
的顶点
,
在边
上,顶点
在边
上.在正三角形
及其内部,以
为位似中心,作正方形
的位似正方形
,且使正方形
的面积最大(不要求写作法);
(2)求(1)中作出的正方形
的边长;
(3)如图
2,在正三角形
中放入正方形
和正方形
,使得
,
在边
上,点
,
分别在边
上,求这两个正方形面积和的最大值及最小值,并说明理由.
答案
第一部分
1.
D
【解析】A.任意两个菱形,各边成比例、各角不一定对应相等,不一定相似,本选项不合题意
B.任意两个矩形,各角对应相等、各边不一定成比例,不一定相似,本选项不合题意;
C.任意两个直角梯形,形状不一定相同,不一定相似,本选项不合题意;
D.任意两个正方形,各角对应相等,各边成比例,一定相似,本选项符合题意.故选D.
2.
B
【解析】,
.
即
,
解得
.
3.
D
4.
B
5.
A
6.
A
7.
A
8.
C
【解析】设小正方形的边长为
,则
的各边分别为
,,.当
是
或
时,
的各边分别是
,,,与
各边成比例,故选C.
9.
A
10.
C
11.
B
12.
A
【解析】过点
作
交
于点
,
,
,
四边形
是菱形,
,
是等边三角形,
,
是等边三角形,
,
,
.
13.
B
【解析】因为
,
所以
,
所以
.
14.
C
15.
C
第二部分
16.
相等,成比例,相等,成比例
17.
或
18.
,,
19.
20.
21.
,
22.
23.
【解析】如图,过点
作
轴于点
,过点
作
轴于点
,
则
,.
,,
,
,
.
在
中,已知
,
设
,则
,利用勾股定理可得
,
解得
.
第三部分
24.
,,
.
,
.
,
,
.
河宽
为
.
25.
(1)
矩形
,矩形
,矩形
,矩形
的长和宽的比不变.
理由如下:设矩形
的宽为
,则长为
,
,,,,,
,,,,
矩形
,矩形
,矩形
,矩形
的长和宽的比不变.
??????(2)
有成比例的线段,如
.
26.
,
,又
,
,
.
27.
在正方形
中,
是
的中点,
.
,
.
又
,
.
在
和
中,
,,
.
28.
(1)
如图
,正方形
即为所求.
??????(2)
设正方形
的边长为
.
为正三角形,
.
.
,即
.
??????(3)
如图,连接
,,,则
.
设正方形
,正方形
的边长分别为
,,它们的面积和为
,则
,.
.
.
延长
交
于点
,则
.
在
中,.
,即
.
所以
.
ⅰ)当
时,即
时,
最小.
.
ⅱ)当
最大,即当
最大且
最小时,
最大.
,由(2)知,.
.
.
第1页(共12
页)
相似三角形
一、选择题(共15小题;共45分)
1.
下列各组图形一定相似的是
A.
两个菱形
B.
两个矩形
C.
两个直角梯形
D.
两个正方形
2.
如图,在
中,,,,,则
的长为
A.
B.
C.
D.
3.
如果
,那么
A.
B.
C.
D.
4.
如图,小正方形的边长均为
,则图中三角形(阴影部分)与
相似的是
A.
B.
C.
D.
5.
已知
,五边形
的最短边为
,最长边为
,五边形
的最长边是
,则五边形
的最短边是
A.
B.
C.
D.
6.
如图,在
中,点
,
分别在边
,
上,若
,则
A.
B.
C.
D.
7.
已知两点
,,先将线段
向左平移一个单位,再以原点
为位似中心,在第一象限内将其缩小为原来的
得到线段
,则点
的对应点
的坐标为
A.
B.
C.
D.
8.
如图,,,,,,,,,
都是方格纸中的格点(即小正方形的顶点),要使
与
相似,则点
应是
,,,
四点中的
A.
或
B.
或
C.
或
D.
或
9.
下列结论中,不正确的是
A.
有一个角相等,两条边对应成比例的两个三角形相似
B.
顺次连接三角形各边中点所得的三角形与原三角形相似
C.
如果三角形两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似
D.
钝角相等的两个等腰三角形相似
10.
应中共中央总书记胡锦涛同志的邀请,中国国民党主席连战先生、亲民党主席宋楚瑜先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的"大唐芙蓉园".该园占地面积约为
,若按比例尺
缩小后,其面积大约相当于
A.
一个篮球场的面积
B.
一张乒乓球台台面的面积
C.
《陕西日报》的一个版面的面积
D.
《数学》课本封面的面积
11.
若一个三角形各边的长度都扩大到原来的
倍,则扩大后的三角形各角的度数都
A.
缩小到原来的
B.
不变
C.
扩大到原来的
倍
D.
扩大到原来的
倍
12.
已知菱形
,,
是动点,边长为
,,,若
,则
A.
B.
C.
D.
13.
中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离
的示意图中,记照板“内芯”的高度为
,观测者的眼睛(图中用点
表示)与
,
在同一水平线上,则下列结论中,正确的是
A.
B.
C.
D.
14.
如图,已知点
,
分别在反比例函数
,
的图象上,且
,则
的值为
A.
B.
C.
D.
15.
如图,,,,.如果
的面积用
表示,
的面积用
表示,那么
A.
B.
C.
D.
二、填空题(共8小题;共40分)
16.
相似三角形的判定定理
(1)两角分别
?
的两个三角形相似;
(2)两边
?
且夹角
?
的两个三角形相似;
(3)三边
?
的两个三角形相似.
17.
如图所示,已知
中,
为边
上一点,
为边
上一点,,,,当
的长度为
?
时,
和
相似.
18.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.如图
,延长矩形
的边
至点
,使
,连接
,如果
,则
?
度;
B.如图
,,,,,则
?,
?.
19.
如图,已知
,且相似比是
,已知
,则
?.
20.
已知
,,
是
,
的比例中项,则
?.
21.
一个三角形的三边之比为
,另一个三角形的最短边长为
,另外两边长为
?时,这两个三角形相似.
22.
如图,线段
两个端点的坐标分别为
,.以原点
为位似中心,在第一象限内将线段
缩小为原来的
后得到线段
,则端点
的坐标为
?.
23.
如图,已知第一象限内的点
在反比例函数
的图象上,第二象限内的点
在反比例函数
的图象上,且
,,则
的面积为
?.
三、解答题(共5小题;共65分)
24.
周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点
,在他们所在的岸边选择了点
,使得
与河岸垂直,并在
点竖起标杆
,再在
的延长线上选择点
竖起标杆
,使得点
与点
,
共线.
已知:,,测得
,,.测量示意图如图所示.请根据相关测量信息,求河宽
.
25.
如图,将一张长宽之比为
的矩形纸片
依次不断对折,可以得到矩形
,矩形
,矩形
,矩形
.
(1)在折叠过程中,这些矩形的长和宽的比变了吗?请说明理由;
(2)在这些矩形中,有成比例的线段吗?
26.
如图,两条直线
,
被三条平行线
,,
所截,且
,,求
的长.
27.
已知:如图,在正方形
中,
是
上的点,且
,
是
的中点.求证:.
28.
如图,正三角形
的边长为
.
(1)如图
1,正方形
的顶点
,
在边
上,顶点
在边
上.在正三角形
及其内部,以
为位似中心,作正方形
的位似正方形
,且使正方形
的面积最大(不要求写作法);
(2)求(1)中作出的正方形
的边长;
(3)如图
2,在正三角形
中放入正方形
和正方形
,使得
,
在边
上,点
,
分别在边
上,求这两个正方形面积和的最大值及最小值,并说明理由.
答案
第一部分
1.
D
【解析】A.任意两个菱形,各边成比例、各角不一定对应相等,不一定相似,本选项不合题意
B.任意两个矩形,各角对应相等、各边不一定成比例,不一定相似,本选项不合题意;
C.任意两个直角梯形,形状不一定相同,不一定相似,本选项不合题意;
D.任意两个正方形,各角对应相等,各边成比例,一定相似,本选项符合题意.故选D.
2.
B
【解析】,
.
即
,
解得
.
3.
D
4.
B
5.
A
6.
A
7.
A
8.
C
【解析】设小正方形的边长为
,则
的各边分别为
,,.当
是
或
时,
的各边分别是
,,,与
各边成比例,故选C.
9.
A
10.
C
11.
B
12.
A
【解析】过点
作
交
于点
,
,
,
四边形
是菱形,
,
是等边三角形,
,
是等边三角形,
,
,
.
13.
B
【解析】因为
,
所以
,
所以
.
14.
C
15.
C
第二部分
16.
相等,成比例,相等,成比例
17.
或
18.
,,
19.
20.
21.
,
22.
23.
【解析】如图,过点
作
轴于点
,过点
作
轴于点
,
则
,.
,,
,
,
.
在
中,已知
,
设
,则
,利用勾股定理可得
,
解得
.
第三部分
24.
,,
.
,
.
,
,
.
河宽
为
.
25.
(1)
矩形
,矩形
,矩形
,矩形
的长和宽的比不变.
理由如下:设矩形
的宽为
,则长为
,
,,,,,
,,,,
矩形
,矩形
,矩形
,矩形
的长和宽的比不变.
??????(2)
有成比例的线段,如
.
26.
,
,又
,
,
.
27.
在正方形
中,
是
的中点,
.
,
.
又
,
.
在
和
中,
,,
.
28.
(1)
如图
,正方形
即为所求.
??????(2)
设正方形
的边长为
.
为正三角形,
.
.
,即
.
??????(3)
如图,连接
,,,则
.
设正方形
,正方形
的边长分别为
,,它们的面积和为
,则
,.
.
.
延长
交
于点
,则
.
在
中,.
,即
.
所以
.
ⅰ)当
时,即
时,
最小.
.
ⅱ)当
最大,即当
最大且
最小时,
最大.
,由(2)知,.
.
.
第1页(共12
页)
同课章节目录
