浙教版九年级数学上册单元卷附答案:第3章 圆的基本性质(Word版)
文档属性
| 名称 | 浙教版九年级数学上册单元卷附答案:第3章 圆的基本性质(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 11:43:30 | ||
图片预览



文档简介
第3章
圆的基本性质
一、选择题(共15小题;共45分)
1.
给出下列说法:①直径是弦;②优弧是半圆;③半径是圆的组成部分;④两个半径不相等的圆中,大的半圆的弧长小于小的半圆的周长.其中正确的有
A.
个
B.
个
C.
个
D.
个
2.
如图,
的半径为
,
为弦,,垂足为
,若
,则弦
的长为
A.
B.
C.
D.
3.
如图,
为
的弦,,则
等于
A.
B.
C.
D.
4.
下列说法中,正确的是
A.
等弦所对的弧相等
B.
等弧所对的弦相等
C.
圆心角相等,则所对的弦也相等
D.
等弦所对的圆心角相等
5.
在平面直角坐标系中,
的圆心在原点上,半径为
,则下面各点在
上的是
A.
B.
C.
D.
6.
已知圆的半径是
,则该圆的内接正三角形的面积是
A.
B.
C.
D.
7.
如图,
的斜边
与量角器的直径恰好重合,
点与
刻度线的一端重合,,射线
绕点
转动,与量角器外沿交于点
,若射线
将
分割出以
为边的等腰三角形,则点
在量角器上对应的度数是
A.
B.
C.
或
D.
或
8.
如图,
的半径
弦
于点
,连接
并延长交
于点
,连接
.若
,,则
的长为
A.
B.
C.
D.
9.
如图,有一圆心角为
,半径长为
的扇形,若将
,
重合后围成一圆锥侧面,那么圆锥的高是
A.
B.
C.
D.
10.
已知
是
的外接圆,
于点
,且
,则
的度数为
A.
B.
C.
或
D.
或
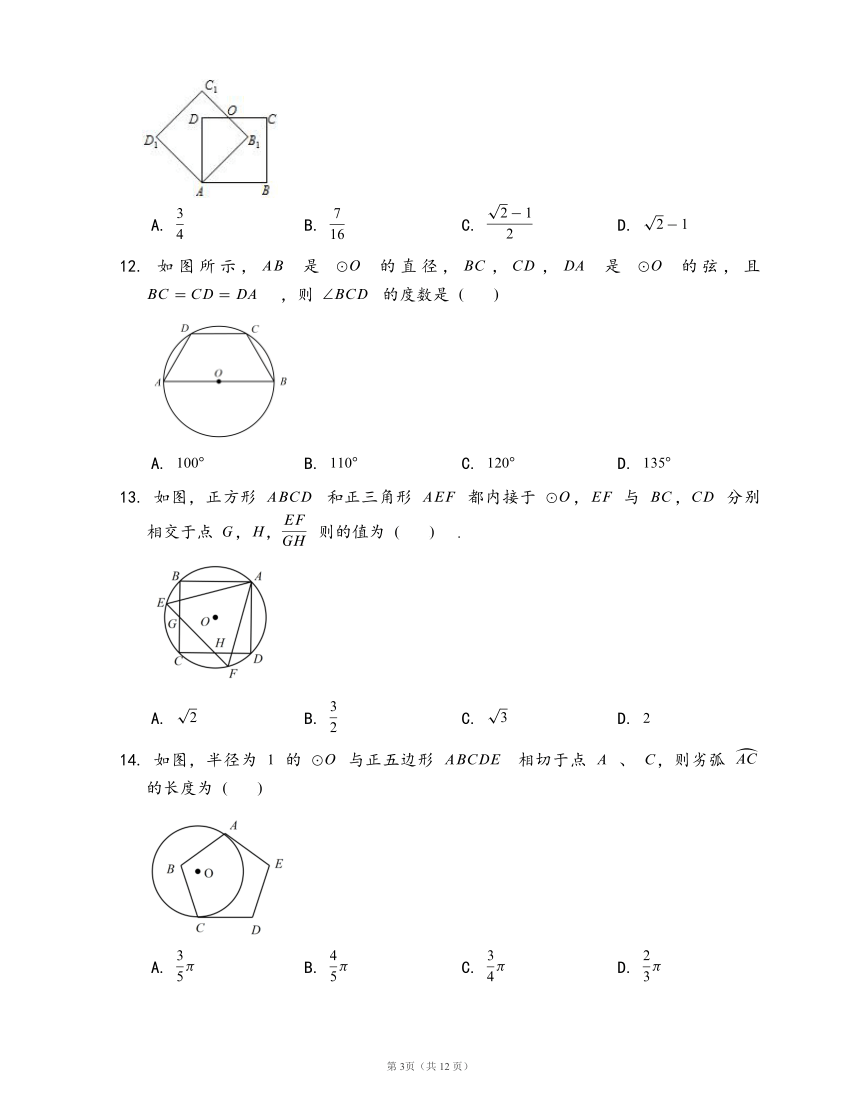
11.
如图,边长为
的正方形
绕点
逆时针旋转
后得到正方形
,边
与
交于点
,则四边形
的面积是
A.
B.
C.
D.
12.
如图所示,
是
的直径,,,
是
的弦,且
,则
的度数是
A.
B.
C.
D.
13.
如图,正方形
和正三角形
都内接于
,
与
,
分别相交于点
,,
则的值为
A.
B.
C.
D.
14.
如图,半径为
的
与正五边形
相切于点
、
,则劣弧
的长度为
A.
B.
C.
D.
15.
如图,将
绕点
顺时针旋转
后,得到
,且
为
的中点,则
等于
A.
;
B.
;
C.
;
D.
;
二、填空题(共8小题;共40分)
16.
如果一个圆锥的母线长为
,底面半径为
,那么这个圆锥的侧面积为
?.
17.
以边长为
的正方形
的顶点
为圆心,以
为半径作
,则点
在
?.(填“外”,“上”或“内”)
18.
如图,
为
的直径,弦
与
交于点
,连接
.若
,,则
?
.
19.
已知正六边形
的边心距为
,则正六边形的半径为
?
.
20.
如图,在等边
中,,
是
的中点,将
绕点
旋转后得到
,那么线段
的长度为
?.
21.
如图,
的直径
垂直弦
于点
,且
,,则
的长为
?.
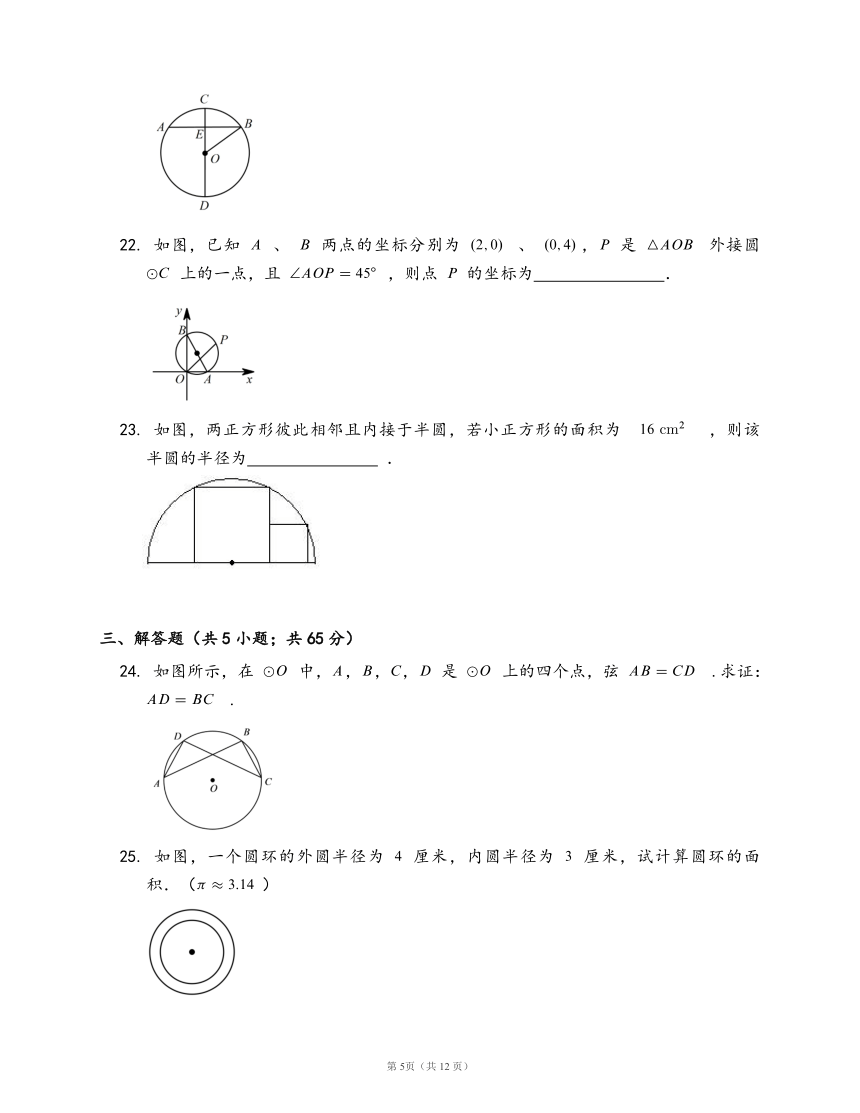
22.
如图,已知
、
两点的坐标分别为
、
,
是
外接圆
上的一点,且
,则点
的坐标为
?.
23.
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
,则该半圆的半径为
?
.
三、解答题(共5小题;共65分)
24.
如图所示,在
中,,,,
是
上的四个点,弦
.求证:
.
25.
如图,一个圆环的外圆半径为
厘米,内圆半径为
厘米,试计算圆环的面积.()
26.
小云出黑板报时遇到了一个难题,在版面设计过程中需要将一个半圆面三等分,请帮她设计一个合理的等分方案,要求尺规作图,保留作图痕迹.
27.
如图,
是
的直径,弦
于点
,,,求
的长.
28.
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,
的三个顶点坐标分别为
,,.
(1)画出
关于
轴对称的
,直接写出点
的坐标
?.
(2)画出
绕点
逆时针旋转
后的
.
(3)在(2)的条件下,求线段
扫过的面积(结果保留
).
答案
第一部分
1.
A
2.
A
3.
D
4.
B
5.
B
6.
B
【解析】由题意画图:
连接
,,过
作
,垂足为
.
是等边三角形,
.
,
,
,
.
.
7.
D
【解析】如图,点
是
中点,连接
.
因为点
在量角器上对应的度数
,
因为当射线
将
分割出以
为边的等腰三角形时,
或
,
所以点
在量角器上对应的度数
或
.
8.
D
【解析】连接
.
是直径,
.
,,
.
设
,则
.
在
中,,解得
,
,.
在
中,.
在
中,.
9.
A
【解析】提示:易得圆锥的弧长为
,
所以圆锥的底面周长为
,底面半径为
,
所以圆锥的高为
.
10.
C
11.
D
【解析】连接
、
.
由题意可知:,
、
、
共线,
,
.
12.
C
【解析】提示:
为等边三角形.
13.
C
【解析】如图,
连接
交
于点
,连接
、
,,
设
的半径是
,
则
,
是
的平分线,
,
,
,
,
,
,
,
,,
,
,
,
即则
的值是
.
14.
B
【解析】因为正五边形
的内角和是
,
则正五边形
的一个内角为:.
连接
、
、
,
圆
与正五边形
相切于点
、
,
,
,
所以劣弧
的长度为:.
故选B.
15.
D
【解析】旋转
后,,,可证
为等边三角形;再根据
,证明
为
的直角三角形,寻找线段
与
之间的数量关系.
第二部分
16.
17.
上
18.
【解析】提示:连接
.
由
是直径可知
,从而求出
.
19.
【解析】如图所示,
连接
,,过
作
,
多边形
是正六边形,
,
,解得
.
20.
21.
【解析】,,
,,.
,
.
22.
【解析】,,
,
,
点横纵坐标相等,可设为
,即
,
,
是直径,
外接圆的圆心为
中点,坐标
,
点在圆上,
点到圆心的距离为圆的半径
.
过点
作
,过点
作
于
交
于
,
,
,,,
根据勾股定理得:,
解得:,
.
23.
第三部分
24.
中的弦
,
.
.
.
25.
(平方厘米).
26.
如图即为所求.
【解析】作
的垂直平分线
交
于点
;
分别以
、
为圆心,以
或
的长为半径画弧,分别交半圆于点
、
;
连接
、
即可.
27.
弦
于点
,,
.
在
中,,,
,
.
28.
(1)
,正确画出对称后的图形.
??????(2)
正确画出旋转后的图形.
??????(3)
.
第3页(共12
页)
圆的基本性质
一、选择题(共15小题;共45分)
1.
给出下列说法:①直径是弦;②优弧是半圆;③半径是圆的组成部分;④两个半径不相等的圆中,大的半圆的弧长小于小的半圆的周长.其中正确的有
A.
个
B.
个
C.
个
D.
个
2.
如图,
的半径为
,
为弦,,垂足为
,若
,则弦
的长为
A.
B.
C.
D.
3.
如图,
为
的弦,,则
等于
A.
B.
C.
D.
4.
下列说法中,正确的是
A.
等弦所对的弧相等
B.
等弧所对的弦相等
C.
圆心角相等,则所对的弦也相等
D.
等弦所对的圆心角相等
5.
在平面直角坐标系中,
的圆心在原点上,半径为
,则下面各点在
上的是
A.
B.
C.
D.
6.
已知圆的半径是
,则该圆的内接正三角形的面积是
A.
B.
C.
D.
7.
如图,
的斜边
与量角器的直径恰好重合,
点与
刻度线的一端重合,,射线
绕点
转动,与量角器外沿交于点
,若射线
将
分割出以
为边的等腰三角形,则点
在量角器上对应的度数是
A.
B.
C.
或
D.
或
8.
如图,
的半径
弦
于点
,连接
并延长交
于点
,连接
.若
,,则
的长为
A.
B.
C.
D.
9.
如图,有一圆心角为
,半径长为
的扇形,若将
,
重合后围成一圆锥侧面,那么圆锥的高是
A.
B.
C.
D.
10.
已知
是
的外接圆,
于点
,且
,则
的度数为
A.
B.
C.
或
D.
或
11.
如图,边长为
的正方形
绕点
逆时针旋转
后得到正方形
,边
与
交于点
,则四边形
的面积是
A.
B.
C.
D.
12.
如图所示,
是
的直径,,,
是
的弦,且
,则
的度数是
A.
B.
C.
D.
13.
如图,正方形
和正三角形
都内接于
,
与
,
分别相交于点
,,
则的值为
A.
B.
C.
D.
14.
如图,半径为
的
与正五边形
相切于点
、
,则劣弧
的长度为
A.
B.
C.
D.
15.
如图,将
绕点
顺时针旋转
后,得到
,且
为
的中点,则
等于
A.
;
B.
;
C.
;
D.
;
二、填空题(共8小题;共40分)
16.
如果一个圆锥的母线长为
,底面半径为
,那么这个圆锥的侧面积为
?.
17.
以边长为
的正方形
的顶点
为圆心,以
为半径作
,则点
在
?.(填“外”,“上”或“内”)
18.
如图,
为
的直径,弦
与
交于点
,连接
.若
,,则
?
.
19.
已知正六边形
的边心距为
,则正六边形的半径为
?
.
20.
如图,在等边
中,,
是
的中点,将
绕点
旋转后得到
,那么线段
的长度为
?.
21.
如图,
的直径
垂直弦
于点
,且
,,则
的长为
?.
22.
如图,已知
、
两点的坐标分别为
、
,
是
外接圆
上的一点,且
,则点
的坐标为
?.
23.
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为
,则该半圆的半径为
?
.
三、解答题(共5小题;共65分)
24.
如图所示,在
中,,,,
是
上的四个点,弦
.求证:
.
25.
如图,一个圆环的外圆半径为
厘米,内圆半径为
厘米,试计算圆环的面积.()
26.
小云出黑板报时遇到了一个难题,在版面设计过程中需要将一个半圆面三等分,请帮她设计一个合理的等分方案,要求尺规作图,保留作图痕迹.
27.
如图,
是
的直径,弦
于点
,,,求
的长.
28.
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,
的三个顶点坐标分别为
,,.
(1)画出
关于
轴对称的
,直接写出点
的坐标
?.
(2)画出
绕点
逆时针旋转
后的
.
(3)在(2)的条件下,求线段
扫过的面积(结果保留
).
答案
第一部分
1.
A
2.
A
3.
D
4.
B
5.
B
6.
B
【解析】由题意画图:
连接
,,过
作
,垂足为
.
是等边三角形,
.
,
,
,
.
.
7.
D
【解析】如图,点
是
中点,连接
.
因为点
在量角器上对应的度数
,
因为当射线
将
分割出以
为边的等腰三角形时,
或
,
所以点
在量角器上对应的度数
或
.
8.
D
【解析】连接
.
是直径,
.
,,
.
设
,则
.
在
中,,解得
,
,.
在
中,.
在
中,.
9.
A
【解析】提示:易得圆锥的弧长为
,
所以圆锥的底面周长为
,底面半径为
,
所以圆锥的高为
.
10.
C
11.
D
【解析】连接
、
.
由题意可知:,
、
、
共线,
,
.
12.
C
【解析】提示:
为等边三角形.
13.
C
【解析】如图,
连接
交
于点
,连接
、
,,
设
的半径是
,
则
,
是
的平分线,
,
,
,
,
,
,
,
,,
,
,
,
即则
的值是
.
14.
B
【解析】因为正五边形
的内角和是
,
则正五边形
的一个内角为:.
连接
、
、
,
圆
与正五边形
相切于点
、
,
,
,
所以劣弧
的长度为:.
故选B.
15.
D
【解析】旋转
后,,,可证
为等边三角形;再根据
,证明
为
的直角三角形,寻找线段
与
之间的数量关系.
第二部分
16.
17.
上
18.
【解析】提示:连接
.
由
是直径可知
,从而求出
.
19.
【解析】如图所示,
连接
,,过
作
,
多边形
是正六边形,
,
,解得
.
20.
21.
【解析】,,
,,.
,
.
22.
【解析】,,
,
,
点横纵坐标相等,可设为
,即
,
,
是直径,
外接圆的圆心为
中点,坐标
,
点在圆上,
点到圆心的距离为圆的半径
.
过点
作
,过点
作
于
交
于
,
,
,,,
根据勾股定理得:,
解得:,
.
23.
第三部分
24.
中的弦
,
.
.
.
25.
(平方厘米).
26.
如图即为所求.
【解析】作
的垂直平分线
交
于点
;
分别以
、
为圆心,以
或
的长为半径画弧,分别交半圆于点
、
;
连接
、
即可.
27.
弦
于点
,,
.
在
中,,,
,
.
28.
(1)
,正确画出对称后的图形.
??????(2)
正确画出旋转后的图形.
??????(3)
.
第3页(共12
页)
同课章节目录
