浙教版九年级数学上册单元卷附答案:第4章 相似三角形(Word版)
文档属性
| 名称 | 浙教版九年级数学上册单元卷附答案:第4章 相似三角形(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 11:46:08 | ||
图片预览



文档简介
第4章
相似三角形
一、选择题(共15小题;共45分)
1.
观察下列各组图形,其中不相似的是
A.
B.
C.
D.
2.
如图,已知直线
,直线
,
与
,,
分别交于点
,,,,,,,,,则
A.
B.
C.
D.
3.
已知
,则下列比例式成立的是
A.
B.
C.
D.
4.
如图,点
在
的边
上,要判断
与
相似,添加一个条件,不正确的是
A.
B.
C.
D.
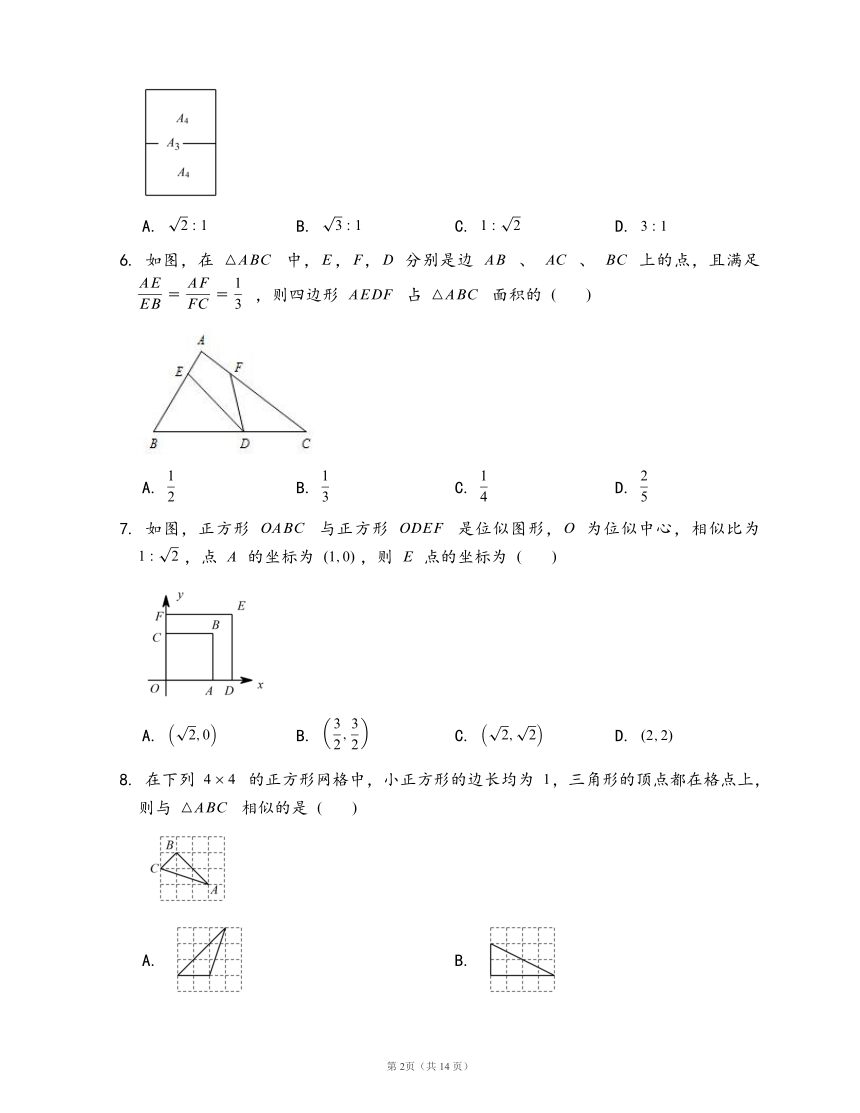
5.
复印纸的型号
,,,,
等,它们之间存在着这样一种关系:将其中某一型号(如
)的复印纸较长边的中点对折后,就能得到两张下一型号()的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为
A.
B.
C.
D.
6.
如图,在
中,,,
分别是边
、
、
上的点,且满足
,则四边形
占
面积的
A.
B.
C.
D.
7.
如图,正方形
与正方形
是位似图形,
为位似中心,相似比为
,点
的坐标为
,则
点的坐标为
A.
B.
C.
D.
8.
在下列
的正方形网格中,小正方形的边长均为
,三角形的顶点都在格点上,则与
相似的是
A.
B.
C.
D.
9.
如图所示,如果
,那么添加下列一个条件后,仍不能确定
的是
A.
B.
C.
D.
10.
为了弘扬雷锋精神,某中学准备在校园内建造一座高
的雷锋人体雕像,向全体师生征集设计方案.小兵同学查阅了有关资料,了解到黄金分割数常用于人体雕像的设计中.如图是小兵同学根据黄金分割数设计的雷锋人体雕像的方案,其中雷锋人体雕像下部的设计高度(精确到
,参考数据:,,)是
A.
B.
C.
D.
11.
如图,如果
与
都是正方形网格中的格点三角形(顶点在格点上),那么
与
的周长比为
A.
B.
C.
D.
12.
如图,已知在
中,点
,,
分别是边
,,
上的点,,,且
,那么
等于
A.
B.
C.
D.
13.
如图,正方形
的边长为
,点
,
分别在边
,
上,,动点
从点
出发沿直线向点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,经过若干次反弹,当动点
第一次回到点
时,动点
所经过的路程长为
A.
B.
C.
D.
14.
在平面直角坐标系中,点
是双曲线
上任意一点,连接
,过点
作
的垂线与双曲线
交于点
,连接
,已知
,则
A.
B.
C.
D.
15.
某小区现有一块等腰直角三角形形状的绿地,腰长为
米,直角顶点为
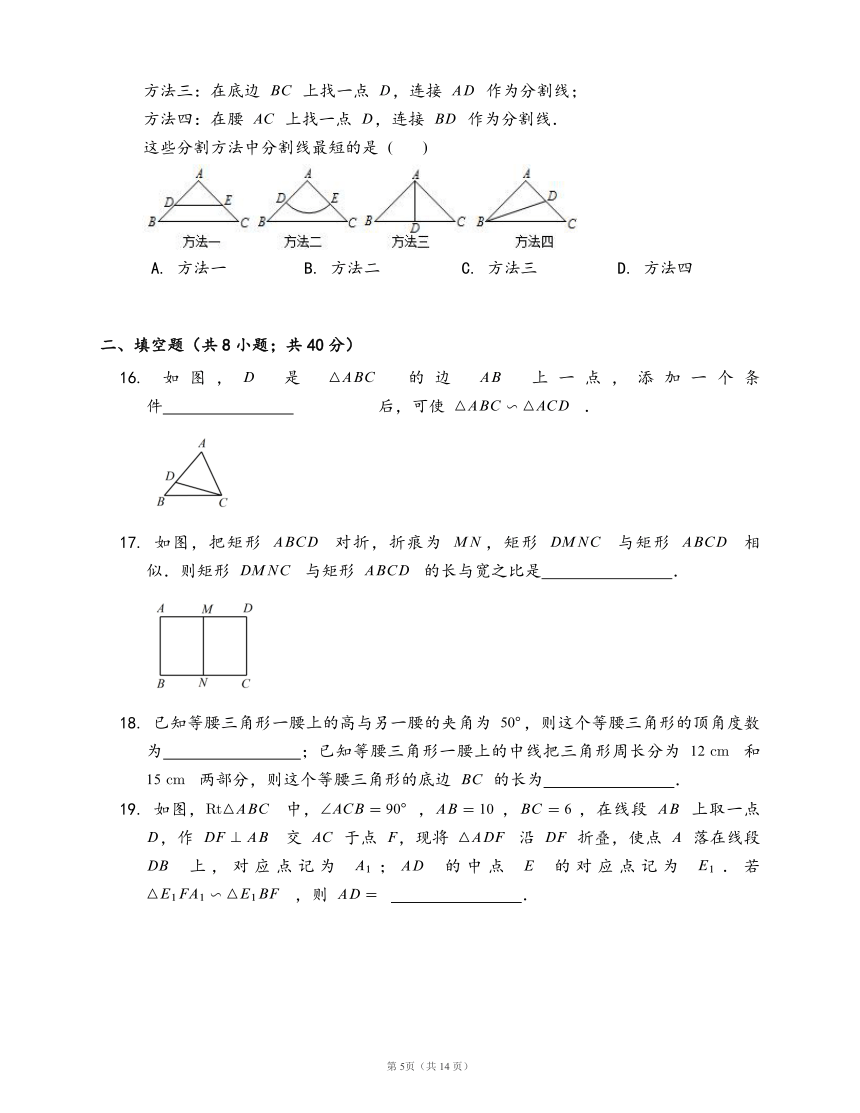
.小区物业管委会准备把它分割成面积相等的两块,有如下的分割方法:
方法一:在腰
上找一点
,作
,交
于点
,
作为分割线;
方法二:以点
为圆心,
为半径作弧,交
于点
,交
于点
,弧
作为分割线;
方法三:在底边
上找一点
,连接
作为分割线;
方法四:在腰
上找一点
,连接
作为分割线.
这些分割方法中分割线最短的是
A.
方法一
B.
方法二
C.
方法三
D.
方法四
二、填空题(共8小题;共40分)
16.
如图,
是
的边
上一点,添加一个条件
?
后,可使
.
17.
如图,把矩形
对折,折痕为
,矩形
与矩形
相似.则矩形
与矩形
的长与宽之比是
?.
18.
已知等腰三角形一腰上的高与另一腰的夹角为
,则这个等腰三角形的顶角度数为
?;已知等腰三角形一腰上的中线把三角形周长分为
和
两部分,则这个等腰三角形的底边
的长为
?.
19.
如图,
中,,,,在线段
上取一点
,作
交
于点
,现将
沿
折叠,使点
落在线段
上,对应点记为
;
的中点
的对应点记为
.若
,则
?.
20.
学校平面图的比例尺是
,平面图上校园面积为
,学校的实际面积是
?
.
21.
在
和
中,,,,,.当
?
时,.
22.
如图,在平面直角坐标系中,正方形
与正方形
是以原点
为位似中心的位似图形,且位似比为
.点
,,
在
轴上,若正方形
的边长为
,则
点坐标为
?.
23.
如图,在平面直角坐标系中,已知点
,
的坐标分别
,,
是
的中点,过点
作
轴的垂线,垂足为
.动点
从点
出发,沿
向点
匀速运动,过点
作
轴的垂线,垂足为
,连接
,.当
所在直线与
所在直线第一次垂直时,点
的坐标为
?.
三、解答题(共5小题;共65分)
24.
一次数学实践课中,小明测量教室前的一棵水杉树高
.他测得
长的竹竿在阳光下的影子是
,当他马上测量树影时,发现树影的上半部分落在墙
上(如图所示).他先测得留在墙上的影高
为
,又测得地面部分的影长
为
.你能帮小明计算出水杉树的树高
是多少吗?
25.
下列各组数能否成比例?如果能成比例,请写出一个比例式.
(1),,,;
(2),,,..
26.
如图,在
中,
是边
的中点,点
在边
上,,
的延长线交于点
.求证:.
27.
如图,
中,,
分别是
,
上的点,且满足
,连接
.
求证:.
28.
已知:如图,在四边形
中,,,,四边形的周长为
,求
和
的长.
答案
第一部分
1.
A
2.
B
3.
B
4.
D
5.
A
6.
C
【解析】
连接
.易证
,
.
和
有同底
,
,
四边形
占
面积的
.
7.
C
【解析】
正方形
与正方形
是位似图形,
为位似中心,相似比为
,
.
点
的坐标为
,即
,
.
四边形
是正方形,
.
点的坐标为
.
8.
B
9.
C
10.
C
【解析】设雷锋人体雕像的下部为
,则上部为
.
由已知可得
,
解得
.
11.
D
【解析】如图,设正方形网格的边长为
,由勾股定理得:
,,
,.
同理可求:,,
,,
.
.
.
12.
A
【解析】因为
,,
所以
.
因为
,
所以
.
13.
C
【解析】根据已知中的点
,
的位置,可知入射角的正切值为
,第一次碰撞点为
,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得,
第二次碰撞点为
,在
上,且
,
第三次碰撞点为
,在
上,且
,
第四次碰撞点为
,在
上,且
,
第五次碰撞点为
,在
上,且
,
第六次回到
点,,
由勾股定理可以得出
,,,,,,
故小球经过的路程为:.
14.
B
【解析】作
轴于
,
轴于
,
点
是双曲线
上的点,点
是双曲线
上的点,
,,
,
,
,
,
,
,
,
,
.
15.
C
【解析】根据等腰直角三角形的性质,
方法一中,,有
,
腰长为
米,
,
;
方法二中,,故
,则
,
故
.
方法三中,;
方法四中,;
则方法三中的分割线最短.
第二部分
16.
(答案不唯一)
17.
【解析】设矩形
的长
,宽
,则
.
矩形
与矩形
相似.
,即
,即
.
.
18.
或
,
或
19.
【解析】在
中,,,
,
.
设
,则
,,,
.
,
,
.
在
中,
,
,
即
,
解得
(舍去),
,
.
20.
21.
22.
23.
【解析】
点
、
的坐标分别为
,
,
,
.
由
,
是
的中点,
可得
,
.
设
,则
.
当
所在直线与
所在直线第一次垂直时,
,
又
,
,
.
.
,即
.
解得
,(舍去).
.
又
,
.
第三部分
24.
连接
,过
作
交
于点
.(),
,
,则
,
().
25.
(1)
,,
,,,
成比例,可以表示为
.
??????(2)
,
,,,
不成比例.
26.
过点
作
,交
于点
.
则
.
.
,
,即
.
27.
因为
,
所以
.
又因为
,
所以
.
所以
.
28.
连接
.
,,
是等边三角形.
.
,
.
,四边形的周长为
,
.
设
.则
.
根据勾股定理
.
解得
.
.
.
第2页(共14
页)
相似三角形
一、选择题(共15小题;共45分)
1.
观察下列各组图形,其中不相似的是
A.
B.
C.
D.
2.
如图,已知直线
,直线
,
与
,,
分别交于点
,,,,,,,,,则
A.
B.
C.
D.
3.
已知
,则下列比例式成立的是
A.
B.
C.
D.
4.
如图,点
在
的边
上,要判断
与
相似,添加一个条件,不正确的是
A.
B.
C.
D.
5.
复印纸的型号
,,,,
等,它们之间存在着这样一种关系:将其中某一型号(如
)的复印纸较长边的中点对折后,就能得到两张下一型号()的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为
A.
B.
C.
D.
6.
如图,在
中,,,
分别是边
、
、
上的点,且满足
,则四边形
占
面积的
A.
B.
C.
D.
7.
如图,正方形
与正方形
是位似图形,
为位似中心,相似比为
,点
的坐标为
,则
点的坐标为
A.
B.
C.
D.
8.
在下列
的正方形网格中,小正方形的边长均为
,三角形的顶点都在格点上,则与
相似的是
A.
B.
C.
D.
9.
如图所示,如果
,那么添加下列一个条件后,仍不能确定
的是
A.
B.
C.
D.
10.
为了弘扬雷锋精神,某中学准备在校园内建造一座高
的雷锋人体雕像,向全体师生征集设计方案.小兵同学查阅了有关资料,了解到黄金分割数常用于人体雕像的设计中.如图是小兵同学根据黄金分割数设计的雷锋人体雕像的方案,其中雷锋人体雕像下部的设计高度(精确到
,参考数据:,,)是
A.
B.
C.
D.
11.
如图,如果
与
都是正方形网格中的格点三角形(顶点在格点上),那么
与
的周长比为
A.
B.
C.
D.
12.
如图,已知在
中,点
,,
分别是边
,,
上的点,,,且
,那么
等于
A.
B.
C.
D.
13.
如图,正方形
的边长为
,点
,
分别在边
,
上,,动点
从点
出发沿直线向点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,经过若干次反弹,当动点
第一次回到点
时,动点
所经过的路程长为
A.
B.
C.
D.
14.
在平面直角坐标系中,点
是双曲线
上任意一点,连接
,过点
作
的垂线与双曲线
交于点
,连接
,已知
,则
A.
B.
C.
D.
15.
某小区现有一块等腰直角三角形形状的绿地,腰长为
米,直角顶点为
.小区物业管委会准备把它分割成面积相等的两块,有如下的分割方法:
方法一:在腰
上找一点
,作
,交
于点
,
作为分割线;
方法二:以点
为圆心,
为半径作弧,交
于点
,交
于点
,弧
作为分割线;
方法三:在底边
上找一点
,连接
作为分割线;
方法四:在腰
上找一点
,连接
作为分割线.
这些分割方法中分割线最短的是
A.
方法一
B.
方法二
C.
方法三
D.
方法四
二、填空题(共8小题;共40分)
16.
如图,
是
的边
上一点,添加一个条件
?
后,可使
.
17.
如图,把矩形
对折,折痕为
,矩形
与矩形
相似.则矩形
与矩形
的长与宽之比是
?.
18.
已知等腰三角形一腰上的高与另一腰的夹角为
,则这个等腰三角形的顶角度数为
?;已知等腰三角形一腰上的中线把三角形周长分为
和
两部分,则这个等腰三角形的底边
的长为
?.
19.
如图,
中,,,,在线段
上取一点
,作
交
于点
,现将
沿
折叠,使点
落在线段
上,对应点记为
;
的中点
的对应点记为
.若
,则
?.
20.
学校平面图的比例尺是
,平面图上校园面积为
,学校的实际面积是
?
.
21.
在
和
中,,,,,.当
?
时,.
22.
如图,在平面直角坐标系中,正方形
与正方形
是以原点
为位似中心的位似图形,且位似比为
.点
,,
在
轴上,若正方形
的边长为
,则
点坐标为
?.
23.
如图,在平面直角坐标系中,已知点
,
的坐标分别
,,
是
的中点,过点
作
轴的垂线,垂足为
.动点
从点
出发,沿
向点
匀速运动,过点
作
轴的垂线,垂足为
,连接
,.当
所在直线与
所在直线第一次垂直时,点
的坐标为
?.
三、解答题(共5小题;共65分)
24.
一次数学实践课中,小明测量教室前的一棵水杉树高
.他测得
长的竹竿在阳光下的影子是
,当他马上测量树影时,发现树影的上半部分落在墙
上(如图所示).他先测得留在墙上的影高
为
,又测得地面部分的影长
为
.你能帮小明计算出水杉树的树高
是多少吗?
25.
下列各组数能否成比例?如果能成比例,请写出一个比例式.
(1),,,;
(2),,,..
26.
如图,在
中,
是边
的中点,点
在边
上,,
的延长线交于点
.求证:.
27.
如图,
中,,
分别是
,
上的点,且满足
,连接
.
求证:.
28.
已知:如图,在四边形
中,,,,四边形的周长为
,求
和
的长.
答案
第一部分
1.
A
2.
B
3.
B
4.
D
5.
A
6.
C
【解析】
连接
.易证
,
.
和
有同底
,
,
四边形
占
面积的
.
7.
C
【解析】
正方形
与正方形
是位似图形,
为位似中心,相似比为
,
.
点
的坐标为
,即
,
.
四边形
是正方形,
.
点的坐标为
.
8.
B
9.
C
10.
C
【解析】设雷锋人体雕像的下部为
,则上部为
.
由已知可得
,
解得
.
11.
D
【解析】如图,设正方形网格的边长为
,由勾股定理得:
,,
,.
同理可求:,,
,,
.
.
.
12.
A
【解析】因为
,,
所以
.
因为
,
所以
.
13.
C
【解析】根据已知中的点
,
的位置,可知入射角的正切值为
,第一次碰撞点为
,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得,
第二次碰撞点为
,在
上,且
,
第三次碰撞点为
,在
上,且
,
第四次碰撞点为
,在
上,且
,
第五次碰撞点为
,在
上,且
,
第六次回到
点,,
由勾股定理可以得出
,,,,,,
故小球经过的路程为:.
14.
B
【解析】作
轴于
,
轴于
,
点
是双曲线
上的点,点
是双曲线
上的点,
,,
,
,
,
,
,
,
,
,
.
15.
C
【解析】根据等腰直角三角形的性质,
方法一中,,有
,
腰长为
米,
,
;
方法二中,,故
,则
,
故
.
方法三中,;
方法四中,;
则方法三中的分割线最短.
第二部分
16.
(答案不唯一)
17.
【解析】设矩形
的长
,宽
,则
.
矩形
与矩形
相似.
,即
,即
.
.
18.
或
,
或
19.
【解析】在
中,,,
,
.
设
,则
,,,
.
,
,
.
在
中,
,
,
即
,
解得
(舍去),
,
.
20.
21.
22.
23.
【解析】
点
、
的坐标分别为
,
,
,
.
由
,
是
的中点,
可得
,
.
设
,则
.
当
所在直线与
所在直线第一次垂直时,
,
又
,
,
.
.
,即
.
解得
,(舍去).
.
又
,
.
第三部分
24.
连接
,过
作
交
于点
.(),
,
,则
,
().
25.
(1)
,,
,,,
成比例,可以表示为
.
??????(2)
,
,,,
不成比例.
26.
过点
作
,交
于点
.
则
.
.
,
,即
.
27.
因为
,
所以
.
又因为
,
所以
.
所以
.
28.
连接
.
,,
是等边三角形.
.
,
.
,四边形的周长为
,
.
设
.则
.
根据勾股定理
.
解得
.
.
.
第2页(共14
页)
同课章节目录
