浙教版八年级数学上册单元卷附答案:第1章 三角形的初步认识(Word版)
文档属性
| 名称 | 浙教版八年级数学上册单元卷附答案:第1章 三角形的初步认识(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 14:34:15 | ||
图片预览




文档简介
第1章
三角形的初步认识
一、选择题(共15小题;共45分)
1.
图中的三角形被木板遮住了一部分,这个三角形是
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
以上都有可能
2.
如图,,,则
A.
垂直平分
B.
垂直平分
C.
平分
D.
以上结论都不正确
3.
下列语句是命题的是
A.
画两条相等的线段
B.
在线段
上取点
C.
等腰三角形是轴对称图形
D.
垂线段最短吗?
4.
在下列条件中,不能判定两个三角形全等的是
A.
两边及其夹角对应相等
B.
两角及其夹边对应相等
C.
两边及一边的对角对应相等
D.
三边对应相等
5.
如图所示,,则图中相等的线段有(不添加其他字母)
A.
对
B.
对
C.
对
D.
对
6.
用反证法证明“”时,应先假设
A.
B.
C.
D.
7.
如图,
中,,
是
的平分线交
于点
,若
,
,
则
的面积是
A.
B.
C.
D.
无法确定
8.
下列给出
个命题:
①
内错角相等;
②
对顶角相等;
③
对于任意实数
,代数式
总是正数;
④
若三条线段
,,
满足
,则三条线段
,,
一定能组成三角形.
其中正确命题的个数是
A.
个
B.
个
C.
个
D.
个
9.
已知三角形的两边长分别为
和
,则下列长度的四条线段中能作为第三边的是
A.
B.
C.
D.
10.
如图,,点
在线段
上,若
,,则
的度数是
A.
B.
C.
D.
11.
如图,已知
,,
与
相交于点
,则图中全等三角形的对数为
A.
B.
C.
D.
12.
用直尺和圆规作一个角等于已知角的示意图如下,则说明
的依据是
A.
B.
C.
D.
13.
如图所示,下面是利用尺规作
的角平分线
的作法,在用尺规作角平分线的过程中,用到的三角形全等的判定方法是
作法:
①以点
为圆心,适当长为半径画弧,分别交
,
于点
,;
②分别以点
,
为圆心,大于
的长为半径画弧,两弧在
内交于一点
;
③画射线
,射线
就是
的角平分线.
A.
B.
C.
D.
14.
在锐角三角形
中,高
和
交于点
,且
,则
的度数是
A.
B.
C.
D.
或
15.
如图,在
中,
为
上一点,,
两点分别在
,
边上.若
,,,则
A.
B.
C.
D.
二、填空题(共7小题;共35分)
16.
如图,已知
,,则补充条件
?
可使
(填写你认为合理的一个条件).
17.
在
和
中,,,,,,,根据
?
可判定
.
18.
如图,在
中,
是
的外角,
与
的平分线相交于点
,
与
的平分线相交于点
,如果
,那么
?
(用含
的代数式表示).
19.
命题“如果,那么,互为相反数”的逆命题为
?.
20.
阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:经过已知直线上一点作这条直线的垂线.
已知:直线
和
上一点
.求作:
的垂线,使它经过点
.
小艾的作法如下:
如图,(1)在直线
上取一点
,使点
与点
不重合,以点
为圆心,
长为半径作弧,交
于
,
两点;
(2)分别以点
和点
为圆心,大于
长为半径作弧,两弧相交于点
;
(3)作直线
.
所以直线
就是所求作的垂线.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是
?.
21.
一个三角形的两边长分别为
和
,第三边长为整数,则这个三角形的周长为
?.
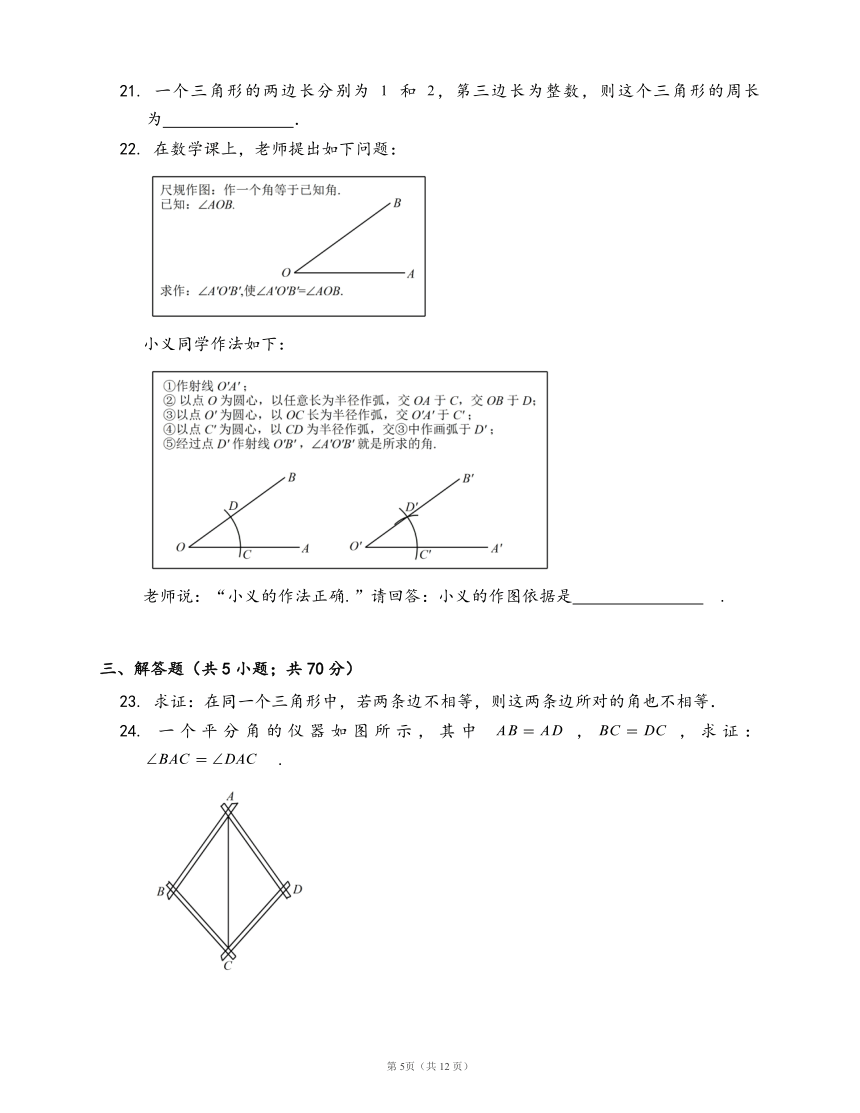
22.
在数学课上,老师提出如下问题:
小义同学作法如下:
老师说:“小义的作法正确.”请回答:小义的作图依据是
?
.
三、解答题(共5小题;共70分)
23.
求证:在同一个三角形中,若两条边不相等,则这两条边所对的角也不相等.
24.
一个平分角的仪器如图所示,其中
,,求证:
.
25.
已知:如图,点
,
在
上,,,,
与
交于点
.求证:.
26.
如图所示,,则图中相等的线段、相等的角各有哪些?图中的
与
,
与
还有怎样的关系?请说明理由.
27.
解答题:
(1)如图①,
的内角
的平分线与外角
的平分线相交于
点,,求
的度数.
(2)如图,四边形
中,设
,,
为四边形
的内角
与外角
的平分线所在直线相交而形成的锐角.
①如图②,若
,求
的度数.(用
,
的代数式表示)
②如图③,若
,请在图③中画出
,并求得
?.(用
,
的代数式表示)
答案
第一部分
1.
D
2.
B
【解析】由已知条件
,利用线段的垂直平分线的性质的逆用可得点
在
的垂直平分线上,同理,点
也在
的垂直平分线上,所以
垂直平分
.
3.
C
4.
C
5.
D
6.
A
7.
A
【解析】作
于
.
是
的平分线,,
,
,
则
的面积
.
8.
B
9.
B
10.
A
【解析】因为
,,,
所以
.
因为
是
的外角,
所以
.
11.
A
12.
A
【解析】作图的步骤:
①以
为圆心,任意长为半径画弧,分别交
、
于点
、
;
②任意作一点
,作射线
,以
为圆心,
长为半径画弧,交
于点
;
③以
为圆心,
长为半径画弧,交前弧于点
;
④过点
作射线
.
所以
就是与
相等的角;
作图完毕.
在
与
,
,
,
,
显然运用的判定方法是
.
13.
C
14.
B
【解析】如图,
为锐角三角形,
高
和
在三角形内.
高
和
交于点
,
.
,,,
.
又
,,
在
与
中,
().
.
,
.
15.
B
【解析】易证
.
.
,
,
.
第二部分
16.
(答案不唯一)
17.
18.
19.
如果,互为相反数,那么
【解析】【分析】根据互逆命题的定义写出逆命题即可.
【解析】解:命题“如果,那么,互为相反数”的逆命题为:
如果,互为相反数,那么;
故答案为:如果,互为相反数,那么.
【点评】本题考查的是命题与定理、互逆命题,掌握逆命题的确定方法是解题的关键.
20.
等腰三角形“三线合一”,两点确定一条直线.
21.
【解析】设第三边为
.
根据三角形的三边关系,得
,即
.
为整数,
的值为
.
三角形的周长为
.
22.
三边分别相等的两个三角形全等;全等三角形对应角相等(写出其中一个即可)
第三部分
23.
假设这两个角相等,那么这两个角所对的边也相等.
这与已知“两条边不相等”相矛盾,所以假设不成立.
24.
在
与
中,
,
.
25.
,,
,,即
,
在
和
中,
,
(全等三角形对应边相等),,
,
,即
.
26.
图中相等的线段有:,,,.
图中相等的角有:,,,.
平行线有:,.
理由:,
,,.
,
.
,
,,,
,.
27.
(1)
的一个内角
的平分线和一个外角
的平分线相交于点
,
,.
??????(2)
①
延长
,
交于点
.
,,,
.
②
【解析】②延长
,
交于点
.
,
同理:
第1页(共12
页)
三角形的初步认识
一、选择题(共15小题;共45分)
1.
图中的三角形被木板遮住了一部分,这个三角形是
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
以上都有可能
2.
如图,,,则
A.
垂直平分
B.
垂直平分
C.
平分
D.
以上结论都不正确
3.
下列语句是命题的是
A.
画两条相等的线段
B.
在线段
上取点
C.
等腰三角形是轴对称图形
D.
垂线段最短吗?
4.
在下列条件中,不能判定两个三角形全等的是
A.
两边及其夹角对应相等
B.
两角及其夹边对应相等
C.
两边及一边的对角对应相等
D.
三边对应相等
5.
如图所示,,则图中相等的线段有(不添加其他字母)
A.
对
B.
对
C.
对
D.
对
6.
用反证法证明“”时,应先假设
A.
B.
C.
D.
7.
如图,
中,,
是
的平分线交
于点
,若
,
,
则
的面积是
A.
B.
C.
D.
无法确定
8.
下列给出
个命题:
①
内错角相等;
②
对顶角相等;
③
对于任意实数
,代数式
总是正数;
④
若三条线段
,,
满足
,则三条线段
,,
一定能组成三角形.
其中正确命题的个数是
A.
个
B.
个
C.
个
D.
个
9.
已知三角形的两边长分别为
和
,则下列长度的四条线段中能作为第三边的是
A.
B.
C.
D.
10.
如图,,点
在线段
上,若
,,则
的度数是
A.
B.
C.
D.
11.
如图,已知
,,
与
相交于点
,则图中全等三角形的对数为
A.
B.
C.
D.
12.
用直尺和圆规作一个角等于已知角的示意图如下,则说明
的依据是
A.
B.
C.
D.
13.
如图所示,下面是利用尺规作
的角平分线
的作法,在用尺规作角平分线的过程中,用到的三角形全等的判定方法是
作法:
①以点
为圆心,适当长为半径画弧,分别交
,
于点
,;
②分别以点
,
为圆心,大于
的长为半径画弧,两弧在
内交于一点
;
③画射线
,射线
就是
的角平分线.
A.
B.
C.
D.
14.
在锐角三角形
中,高
和
交于点
,且
,则
的度数是
A.
B.
C.
D.
或
15.
如图,在
中,
为
上一点,,
两点分别在
,
边上.若
,,,则
A.
B.
C.
D.
二、填空题(共7小题;共35分)
16.
如图,已知
,,则补充条件
?
可使
(填写你认为合理的一个条件).
17.
在
和
中,,,,,,,根据
?
可判定
.
18.
如图,在
中,
是
的外角,
与
的平分线相交于点
,
与
的平分线相交于点
,如果
,那么
?
(用含
的代数式表示).
19.
命题“如果,那么,互为相反数”的逆命题为
?.
20.
阅读下面材料:
数学课上,老师提出如下问题:
尺规作图:经过已知直线上一点作这条直线的垂线.
已知:直线
和
上一点
.求作:
的垂线,使它经过点
.
小艾的作法如下:
如图,(1)在直线
上取一点
,使点
与点
不重合,以点
为圆心,
长为半径作弧,交
于
,
两点;
(2)分别以点
和点
为圆心,大于
长为半径作弧,两弧相交于点
;
(3)作直线
.
所以直线
就是所求作的垂线.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是
?.
21.
一个三角形的两边长分别为
和
,第三边长为整数,则这个三角形的周长为
?.
22.
在数学课上,老师提出如下问题:
小义同学作法如下:
老师说:“小义的作法正确.”请回答:小义的作图依据是
?
.
三、解答题(共5小题;共70分)
23.
求证:在同一个三角形中,若两条边不相等,则这两条边所对的角也不相等.
24.
一个平分角的仪器如图所示,其中
,,求证:
.
25.
已知:如图,点
,
在
上,,,,
与
交于点
.求证:.
26.
如图所示,,则图中相等的线段、相等的角各有哪些?图中的
与
,
与
还有怎样的关系?请说明理由.
27.
解答题:
(1)如图①,
的内角
的平分线与外角
的平分线相交于
点,,求
的度数.
(2)如图,四边形
中,设
,,
为四边形
的内角
与外角
的平分线所在直线相交而形成的锐角.
①如图②,若
,求
的度数.(用
,
的代数式表示)
②如图③,若
,请在图③中画出
,并求得
?.(用
,
的代数式表示)
答案
第一部分
1.
D
2.
B
【解析】由已知条件
,利用线段的垂直平分线的性质的逆用可得点
在
的垂直平分线上,同理,点
也在
的垂直平分线上,所以
垂直平分
.
3.
C
4.
C
5.
D
6.
A
7.
A
【解析】作
于
.
是
的平分线,,
,
,
则
的面积
.
8.
B
9.
B
10.
A
【解析】因为
,,,
所以
.
因为
是
的外角,
所以
.
11.
A
12.
A
【解析】作图的步骤:
①以
为圆心,任意长为半径画弧,分别交
、
于点
、
;
②任意作一点
,作射线
,以
为圆心,
长为半径画弧,交
于点
;
③以
为圆心,
长为半径画弧,交前弧于点
;
④过点
作射线
.
所以
就是与
相等的角;
作图完毕.
在
与
,
,
,
,
显然运用的判定方法是
.
13.
C
14.
B
【解析】如图,
为锐角三角形,
高
和
在三角形内.
高
和
交于点
,
.
,,,
.
又
,,
在
与
中,
().
.
,
.
15.
B
【解析】易证
.
.
,
,
.
第二部分
16.
(答案不唯一)
17.
18.
19.
如果,互为相反数,那么
【解析】【分析】根据互逆命题的定义写出逆命题即可.
【解析】解:命题“如果,那么,互为相反数”的逆命题为:
如果,互为相反数,那么;
故答案为:如果,互为相反数,那么.
【点评】本题考查的是命题与定理、互逆命题,掌握逆命题的确定方法是解题的关键.
20.
等腰三角形“三线合一”,两点确定一条直线.
21.
【解析】设第三边为
.
根据三角形的三边关系,得
,即
.
为整数,
的值为
.
三角形的周长为
.
22.
三边分别相等的两个三角形全等;全等三角形对应角相等(写出其中一个即可)
第三部分
23.
假设这两个角相等,那么这两个角所对的边也相等.
这与已知“两条边不相等”相矛盾,所以假设不成立.
24.
在
与
中,
,
.
25.
,,
,,即
,
在
和
中,
,
(全等三角形对应边相等),,
,
,即
.
26.
图中相等的线段有:,,,.
图中相等的角有:,,,.
平行线有:,.
理由:,
,,.
,
.
,
,,,
,.
27.
(1)
的一个内角
的平分线和一个外角
的平分线相交于点
,
,.
??????(2)
①
延长
,
交于点
.
,,,
.
②
【解析】②延长
,
交于点
.
,
同理:
第1页(共12
页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
