浙教版八年级数学上册第4章 图形与坐标单元满分冲刺卷(word版,含解析)
文档属性
| 名称 | 浙教版八年级数学上册第4章 图形与坐标单元满分冲刺卷(word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 14:31:36 | ||
图片预览




文档简介
第4章
图形与坐标
一、选择题(共16小题;共48分)
1.
下图所示的四条射线中,表示北偏西
的是
A.
射线
B.
射线
C.
射线
D.
射线
2.
在平面直角坐标系中,已知点
,则点
在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3.
“健步走”越来越受到人们的喜爱.一个健步走小组将自己的活动场地定在奥林匹克公园(路线:森林公园——
玲珑塔
——
国家体育场——水立方),如图,假设在奥林匹克公园设计图上规定玲珑塔的坐标为
,森林公园的坐标为
,则终点水立方的坐标为
A.
B.
C.
D.
4.
下列说法错误的是
A.
当横坐标乘以
,纵坐标不变时,所得图形与原图形关于
轴对称
B.
当横坐标不变,纵坐标乘以
时,所得图形与原图形关于
轴对称
C.
当横、纵坐标都加上(或减去)
时,所得图形与原图形关于原点对称
D.
当横、纵坐标都乘以
时,所得图形与原图形关于原点对称
5.
平面直角坐标系中点
到
轴的距离是
,到
轴的距离是
,则这样的点
共有
A.
个
B.
个
C.
个
D.
个
6.
若点
在
轴上,则点
在第
象限.
A.
一
B.
二
C.
三
D.
四
7.
在国外留学的叔叔送给聪聪一个新奇的玩具——智能流氓兔.它的新奇之处在于若第一次向正南跳一下,第二次就掉头向正北跳两下,第三次又掉头向正南跳三下……而且每一跳的距离为
.如果流氓兔位于原点处,第一次向正南跳(记
轴正半轴方向为正北,
个单位为
),那么跳完第
次后,流氓兔所在位置的坐标为
A.
B.
C.
D.
8.
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于
轴的正方形:边长为
的正方形内部有
个整点,边长为
的正方形内部有
个整点,边长为
的正方形内部有
个整点,,则边长为
的正方形内部的整点有
A.
个
B.
个
C.
个
D.
个
9.
如图,
处在
处的南偏西
方向,
处在
处的南偏东
方向,
处在
处的北偏东
方向,则
等于
A.
B.
C.
D.
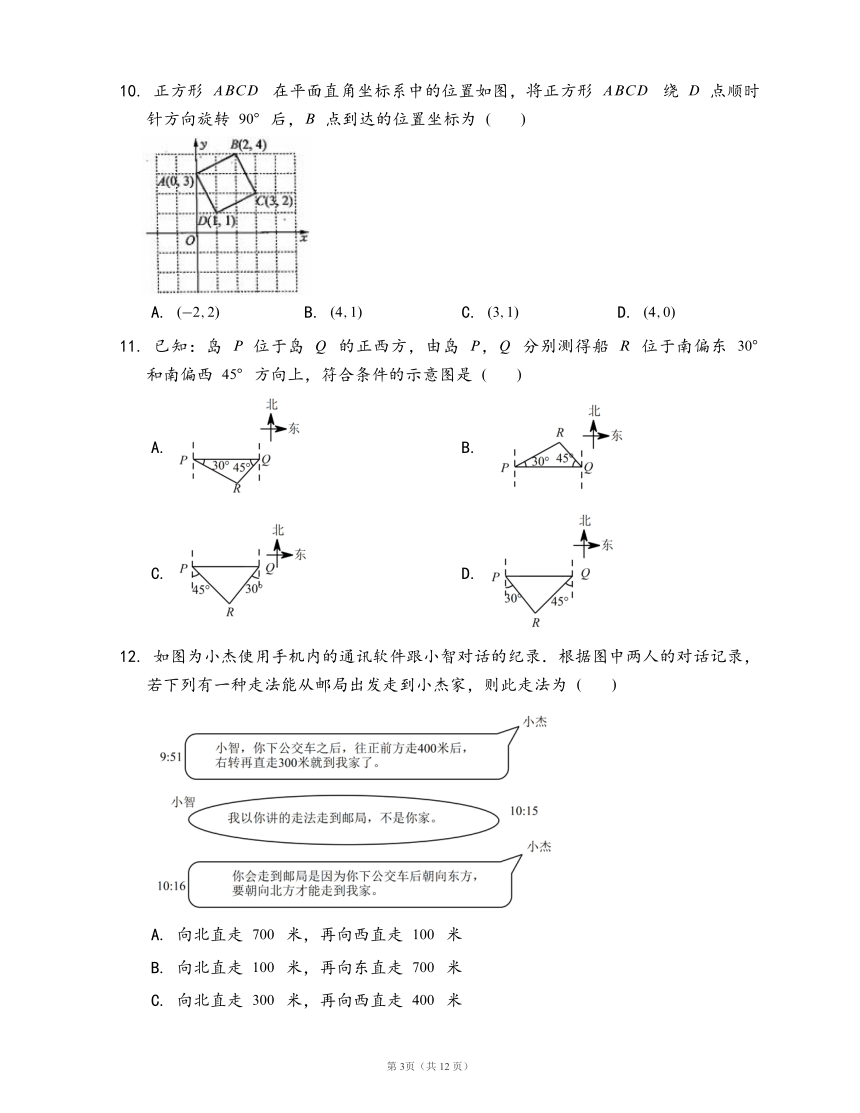
10.
正方形
在平面直角坐标系中的位置如图,将正方形
绕
点顺时针方向旋转
后,
点到达的位置坐标为
A.
B.
C.
D.
11.
已知:岛
位于岛
的正西方,由岛
,
分别测得船
位于南偏东
和南偏西
方向上,符合条件的示意图是
A.
B.
C.
D.
12.
如图为小杰使用手机内的通讯软件跟小智对话的纪录.根据图中两人的对话记录,若下列有一种走法能从邮局出发走到小杰家,则此走法为
A.
向北直走
米,再向西直走
米
B.
向北直走
米,再向东直走
米
C.
向北直走
米,再向西直走
米
D.
向北直走
米,再向东直走
米
13.
在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第
步向右走
个单位,第
步向右走
个单位,第
步向上走
个单位,第
步向右走
个单位
依此类推,第
步的走法是:当
能被
整除时,则向上走
个单位;当
被
除,余数为
时,则向右走
个单位;当
被
除,余数为
时,则向右走
个单位,当走完第
步时,棋子所处位置的坐标是
A.
B.
C.
D.
14.
已知点
在第一、三象限的角平分线上,则
的坐标为
A.
B.
C.
D.
15.
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用
表示,小军的位置用
表示,那么你的位置可以表示成
A.
B.
C.
D.
16.
如图,在平面直角坐标系中,已知点
,,,,动点
从点
出发,以每秒
个单位的速度按逆时针方向沿四边形
的边做环绕运动;另一动点
从点
出发,以每秒
个单位的速度按顺时针方向沿四边形
的边做环绕运动,则第
次相遇点的坐标是
A.
B.
C.
D.
二、填空题(共8小题;共40分)
17.
小红坐在第
排
号用
表示,则
表示小红坐在第
?排
?号.
18.
若点
在第三象限,则点
在第
?象限.
19.
如图所示是台州市地图的一部分,分别以正东、正北方向为
轴、
轴的正方向建立直角坐标系,规定一个单位长度表示
.甲、乙两人对着地图如下描述路桥区
处的位置,则椒江区
处的坐标是
?.
20.
如图,在平面直角坐标系中,直线
是第一、三象限的角平分线.
实验与探究:
①由图观察易知
关于直线
的对称点
的坐标为
,请在图中分别标明
,
关于直线
的对称点
、
的位置,并写出他们的坐标:
?,
?;
归纳与发现:
②结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
关于第一、三象限的角平分线
的对称点
的坐标为
?(不必证明);
③点
在直线
的下方,则
,
的大小关系为
?;若在直线
的上方,则
?.
21.
东方红电影院一张
排
号的电影票若用
表示,则
表示的实际意义是
?.
22.
五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋
所在点的坐标是
,黑棋
所在点的坐标是
,现在轮到黑棋走,黑棋放到点
的位置就获得胜利,点
的坐标是
?.
23.
在平面直角坐标系中有一个已知点
,现在
轴向下平移
个单位,
轴向左平移
个单位,单位长度不变,得到新的坐标系,在新的坐标系下点
的坐标为(
,
),在旧的坐标系下,点
的坐标为
?;
24.
如图,
点的坐标为
,
点的坐标为
,
点的坐标为
,
点的坐标为
.小明发现:线段
与线段
存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是
?.
三、解答题(共5小题;共62分)
25.
在我国沿海地区,几乎每年夏秋两季都会或多或少地遭受台风的侵袭,加强台风的监测和预报,是减轻台风灾害的重要措施.下表是中央气象台
年发布的第
号台风“鲇鱼”的有关信息:
请在下面的经纬度地图上找到台风中心在
日
时和
日
时所在的位置.
26.
已知,
三个顶点的坐标分别为
,,.
(1)在网格中建立平面直角标系并画出
;
(2)求出
的面积;
(3)在图中作出
关于
轴对称的图形
,并写出点
,,
的坐标.
27.
如图,已知
,,,.
(1)求三角形
的面积;
(2)设
为坐标轴上一点,若
,求
点的坐标.
28.
我们知道,如果已知一点
相对于定点
的距离和方向,那么这个点就被唯一确定了.这就是说,我们可用角度和距离来确定平面上点的相对位置.如图①,在平面内取一定点
,叫做极点,引一条射线
,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任一点
,用
表示线段
的长度,
表示从
到
的角度,
叫做点
的极径,
叫做点
的极角,有序数对
就叫做点
的极坐标,这样就在平面上建立了极坐标系,极坐标为
的点
可表示为
.建立极坐标后,给定
和
就可以在平面内唯一确定一点
.如图②,如果点
的位置为
,点
的位置为
.
①
②
(1)请分别表示出点
与点
的位置.
(2)若以
为极点,
为极轴,分别写出点
,,
的极坐标.
29.
如图,在平面直角坐标系中,已知点
,
轴于
点.
(1)将点
绕原点逆时针方向旋转
后到点
点,求点
的坐标.
(2)将
平移得到
,点
的对应点是
,在坐标系中作出
,并写出点
和
的坐标.
答案
第一部分
1.
D
2.
B
【解析】点
在第二象限.
3.
A
4.
C
5.
D
6.
B
【解析】
点
在
轴上,
,即
,
则点
坐标为
,
点
在第二象限.
7.
C
【解析】用“”表示正南方向,用“”表示正北方向.
根据题意,得
流氓兔最后所在位置的坐标为
.
8.
B
【解析】设边长为
的正方形内部的整点的坐标为
,x,y都为整数.
则
,
.
故
只可取
,,,,,,
共
个,
只可取
,,,,,,
共
个.
它们共可组成点
的数目为
(个).
9.
C
10.
D
11.
D
12.
A
13.
C
14.
C
15.
D
16.
A
【解析】
,,,
,,即
.
经过
秒钟时,
与
在
处相遇.
接下来两个点走的路程为
的倍数时,两点相遇,
第二次相遇在
的中点
,
第三次相遇在
,
第四次相遇在
,
第五次相遇在
,
第六次相遇在
点
,
每五次相遇点重合一次,
,
即第
次相遇点的坐标与第四次相遇点的坐标重合,即
.
第二部分
17.
,
18.
一
19.
【解析】如图所示,连接
,作
轴于
点.
根据题意,可得
,,,.
所以
.
所以
点坐标为
.
20.
,,,,
21.
排
号
22.
23.
24.
或
第三部分
25.
26.
(1)
所作图形如图
所示:
??????(2)
.
??????(3)
所作图形如图
所示:
,,.
27.
(1)
,,,
,
.
??????(2)
当
在
轴上时,设
点坐标为
,
,解得
,;
当
在
轴上时,设
点坐标为
,
,
,
,解得
,.
点坐标为
或
或
或
.
28.
(1)
点
;.
??????(2)
点
的极径为
,极角为
;点
的极径为
,极角为
;点
的极径为
,极角为
,
点
,,.
29.
(1)
.
??????(2)
,.
第12页(共12
页)
图形与坐标
一、选择题(共16小题;共48分)
1.
下图所示的四条射线中,表示北偏西
的是
A.
射线
B.
射线
C.
射线
D.
射线
2.
在平面直角坐标系中,已知点
,则点
在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3.
“健步走”越来越受到人们的喜爱.一个健步走小组将自己的活动场地定在奥林匹克公园(路线:森林公园——
玲珑塔
——
国家体育场——水立方),如图,假设在奥林匹克公园设计图上规定玲珑塔的坐标为
,森林公园的坐标为
,则终点水立方的坐标为
A.
B.
C.
D.
4.
下列说法错误的是
A.
当横坐标乘以
,纵坐标不变时,所得图形与原图形关于
轴对称
B.
当横坐标不变,纵坐标乘以
时,所得图形与原图形关于
轴对称
C.
当横、纵坐标都加上(或减去)
时,所得图形与原图形关于原点对称
D.
当横、纵坐标都乘以
时,所得图形与原图形关于原点对称
5.
平面直角坐标系中点
到
轴的距离是
,到
轴的距离是
,则这样的点
共有
A.
个
B.
个
C.
个
D.
个
6.
若点
在
轴上,则点
在第
象限.
A.
一
B.
二
C.
三
D.
四
7.
在国外留学的叔叔送给聪聪一个新奇的玩具——智能流氓兔.它的新奇之处在于若第一次向正南跳一下,第二次就掉头向正北跳两下,第三次又掉头向正南跳三下……而且每一跳的距离为
.如果流氓兔位于原点处,第一次向正南跳(记
轴正半轴方向为正北,
个单位为
),那么跳完第
次后,流氓兔所在位置的坐标为
A.
B.
C.
D.
8.
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于
轴的正方形:边长为
的正方形内部有
个整点,边长为
的正方形内部有
个整点,边长为
的正方形内部有
个整点,,则边长为
的正方形内部的整点有
A.
个
B.
个
C.
个
D.
个
9.
如图,
处在
处的南偏西
方向,
处在
处的南偏东
方向,
处在
处的北偏东
方向,则
等于
A.
B.
C.
D.
10.
正方形
在平面直角坐标系中的位置如图,将正方形
绕
点顺时针方向旋转
后,
点到达的位置坐标为
A.
B.
C.
D.
11.
已知:岛
位于岛
的正西方,由岛
,
分别测得船
位于南偏东
和南偏西
方向上,符合条件的示意图是
A.
B.
C.
D.
12.
如图为小杰使用手机内的通讯软件跟小智对话的纪录.根据图中两人的对话记录,若下列有一种走法能从邮局出发走到小杰家,则此走法为
A.
向北直走
米,再向西直走
米
B.
向北直走
米,再向东直走
米
C.
向北直走
米,再向西直走
米
D.
向北直走
米,再向东直走
米
13.
在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第
步向右走
个单位,第
步向右走
个单位,第
步向上走
个单位,第
步向右走
个单位
依此类推,第
步的走法是:当
能被
整除时,则向上走
个单位;当
被
除,余数为
时,则向右走
个单位;当
被
除,余数为
时,则向右走
个单位,当走完第
步时,棋子所处位置的坐标是
A.
B.
C.
D.
14.
已知点
在第一、三象限的角平分线上,则
的坐标为
A.
B.
C.
D.
15.
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用
表示,小军的位置用
表示,那么你的位置可以表示成
A.
B.
C.
D.
16.
如图,在平面直角坐标系中,已知点
,,,,动点
从点
出发,以每秒
个单位的速度按逆时针方向沿四边形
的边做环绕运动;另一动点
从点
出发,以每秒
个单位的速度按顺时针方向沿四边形
的边做环绕运动,则第
次相遇点的坐标是
A.
B.
C.
D.
二、填空题(共8小题;共40分)
17.
小红坐在第
排
号用
表示,则
表示小红坐在第
?排
?号.
18.
若点
在第三象限,则点
在第
?象限.
19.
如图所示是台州市地图的一部分,分别以正东、正北方向为
轴、
轴的正方向建立直角坐标系,规定一个单位长度表示
.甲、乙两人对着地图如下描述路桥区
处的位置,则椒江区
处的坐标是
?.
20.
如图,在平面直角坐标系中,直线
是第一、三象限的角平分线.
实验与探究:
①由图观察易知
关于直线
的对称点
的坐标为
,请在图中分别标明
,
关于直线
的对称点
、
的位置,并写出他们的坐标:
?,
?;
归纳与发现:
②结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
关于第一、三象限的角平分线
的对称点
的坐标为
?(不必证明);
③点
在直线
的下方,则
,
的大小关系为
?;若在直线
的上方,则
?.
21.
东方红电影院一张
排
号的电影票若用
表示,则
表示的实际意义是
?.
22.
五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋
所在点的坐标是
,黑棋
所在点的坐标是
,现在轮到黑棋走,黑棋放到点
的位置就获得胜利,点
的坐标是
?.
23.
在平面直角坐标系中有一个已知点
,现在
轴向下平移
个单位,
轴向左平移
个单位,单位长度不变,得到新的坐标系,在新的坐标系下点
的坐标为(
,
),在旧的坐标系下,点
的坐标为
?;
24.
如图,
点的坐标为
,
点的坐标为
,
点的坐标为
,
点的坐标为
.小明发现:线段
与线段
存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是
?.
三、解答题(共5小题;共62分)
25.
在我国沿海地区,几乎每年夏秋两季都会或多或少地遭受台风的侵袭,加强台风的监测和预报,是减轻台风灾害的重要措施.下表是中央气象台
年发布的第
号台风“鲇鱼”的有关信息:
请在下面的经纬度地图上找到台风中心在
日
时和
日
时所在的位置.
26.
已知,
三个顶点的坐标分别为
,,.
(1)在网格中建立平面直角标系并画出
;
(2)求出
的面积;
(3)在图中作出
关于
轴对称的图形
,并写出点
,,
的坐标.
27.
如图,已知
,,,.
(1)求三角形
的面积;
(2)设
为坐标轴上一点,若
,求
点的坐标.
28.
我们知道,如果已知一点
相对于定点
的距离和方向,那么这个点就被唯一确定了.这就是说,我们可用角度和距离来确定平面上点的相对位置.如图①,在平面内取一定点
,叫做极点,引一条射线
,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任一点
,用
表示线段
的长度,
表示从
到
的角度,
叫做点
的极径,
叫做点
的极角,有序数对
就叫做点
的极坐标,这样就在平面上建立了极坐标系,极坐标为
的点
可表示为
.建立极坐标后,给定
和
就可以在平面内唯一确定一点
.如图②,如果点
的位置为
,点
的位置为
.
①
②
(1)请分别表示出点
与点
的位置.
(2)若以
为极点,
为极轴,分别写出点
,,
的极坐标.
29.
如图,在平面直角坐标系中,已知点
,
轴于
点.
(1)将点
绕原点逆时针方向旋转
后到点
点,求点
的坐标.
(2)将
平移得到
,点
的对应点是
,在坐标系中作出
,并写出点
和
的坐标.
答案
第一部分
1.
D
2.
B
【解析】点
在第二象限.
3.
A
4.
C
5.
D
6.
B
【解析】
点
在
轴上,
,即
,
则点
坐标为
,
点
在第二象限.
7.
C
【解析】用“”表示正南方向,用“”表示正北方向.
根据题意,得
流氓兔最后所在位置的坐标为
.
8.
B
【解析】设边长为
的正方形内部的整点的坐标为
,x,y都为整数.
则
,
.
故
只可取
,,,,,,
共
个,
只可取
,,,,,,
共
个.
它们共可组成点
的数目为
(个).
9.
C
10.
D
11.
D
12.
A
13.
C
14.
C
15.
D
16.
A
【解析】
,,,
,,即
.
经过
秒钟时,
与
在
处相遇.
接下来两个点走的路程为
的倍数时,两点相遇,
第二次相遇在
的中点
,
第三次相遇在
,
第四次相遇在
,
第五次相遇在
,
第六次相遇在
点
,
每五次相遇点重合一次,
,
即第
次相遇点的坐标与第四次相遇点的坐标重合,即
.
第二部分
17.
,
18.
一
19.
【解析】如图所示,连接
,作
轴于
点.
根据题意,可得
,,,.
所以
.
所以
点坐标为
.
20.
,,,,
21.
排
号
22.
23.
24.
或
第三部分
25.
26.
(1)
所作图形如图
所示:
??????(2)
.
??????(3)
所作图形如图
所示:
,,.
27.
(1)
,,,
,
.
??????(2)
当
在
轴上时,设
点坐标为
,
,解得
,;
当
在
轴上时,设
点坐标为
,
,
,
,解得
,.
点坐标为
或
或
或
.
28.
(1)
点
;.
??????(2)
点
的极径为
,极角为
;点
的极径为
,极角为
;点
的极径为
,极角为
,
点
,,.
29.
(1)
.
??????(2)
,.
第12页(共12
页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
