浙教版九年级数学上册第四章相似三角形综合测试卷(Word版 含答案)
文档属性
| 名称 | 浙教版九年级数学上册第四章相似三角形综合测试卷(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览



文档简介
第四章
相似三角形综合测试卷
一.选择题
1.如图,已知AD与BC相交于点O,AB∥CD,如果∠B=40°,∠D=30°,则∠AOC=(
)
A.
60°
B.
70°
C.
80°
D.
120°
2.已知线段a=4,b=9,线段x是a,b的比例中项,则x等于( )
A.
6
B.
6或-6
C.
-6
D.
36
3.如图,A﹑B两点分别位于一个池塘的两端,小明想用绳子测量A﹑B间的距离,但绳子不够,于是他想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,在AC的延长线上取一点D,使CD=CA,在BC的延长线上取一点E,使CE=CB,测得DE的长为5米,则AB两点间的距离为( )
A.
6米
B.
8米
C.
10米
D.
12米
4.如图,直线l
1∥l2∥l3
,
直线AC分别交l1
,
l2
,
l3于点A,B,C,直线DF分别交l1
,
l2
,
l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是(??????)
A.
3
B.
C.
D.
5.如图,在△ABC中,DE∥FG∥BC,AD:DF:FB=3:2:1,则△ADE,四边形DFGE,四边形FBCG的面积比为( )
A.
3:2:1
B.
9:4:1
C.
9:16:11
D.
9:25:36
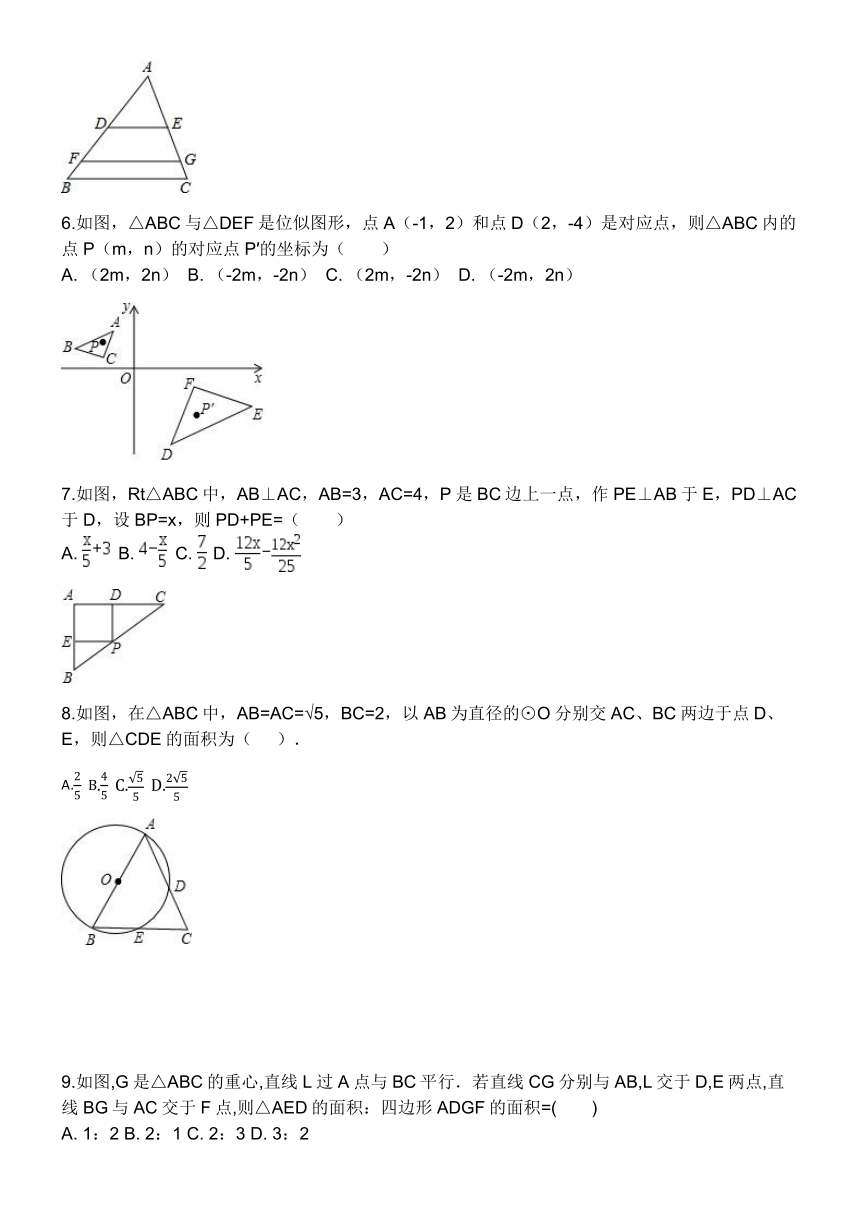
6.如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
A.
(2m,2n)
B.
(-2m,-2n)
C.
(2m,-2n)
D.
(-2m,2n)
7.如图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=( )
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC=√5,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为(
).
A.
B.
C.
D.
9.如图,G是△ABC的重心,直线L过A点与BC平行.若直线CG分别与AB,L交于D,E两点,直线BG与AC交于F点,则△AED的面积:四边形ADGF的面积=( )
A.
1:2
B.
2:1
C.
2:3
D.
3:2
10.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=;③
.
其中正确的是( )
A.
①②
B.
②③
C.
①③
D.
①②③
二.填空题
11.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为____.
12.已知,则
13.如图,E为ABCD的边AD延长线上一点,且D为AE的黄金分割点,即AD=AE,BE交DC于点F,已知AB=+1,则CF的长是________.
14.顶角是36°的等腰三角形称为黄金三角形,如图,在△ABC中,AB=AC=1,∠A=36°,BD是△ABC的角平分线,那么AD=
.
15.如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为____
16.
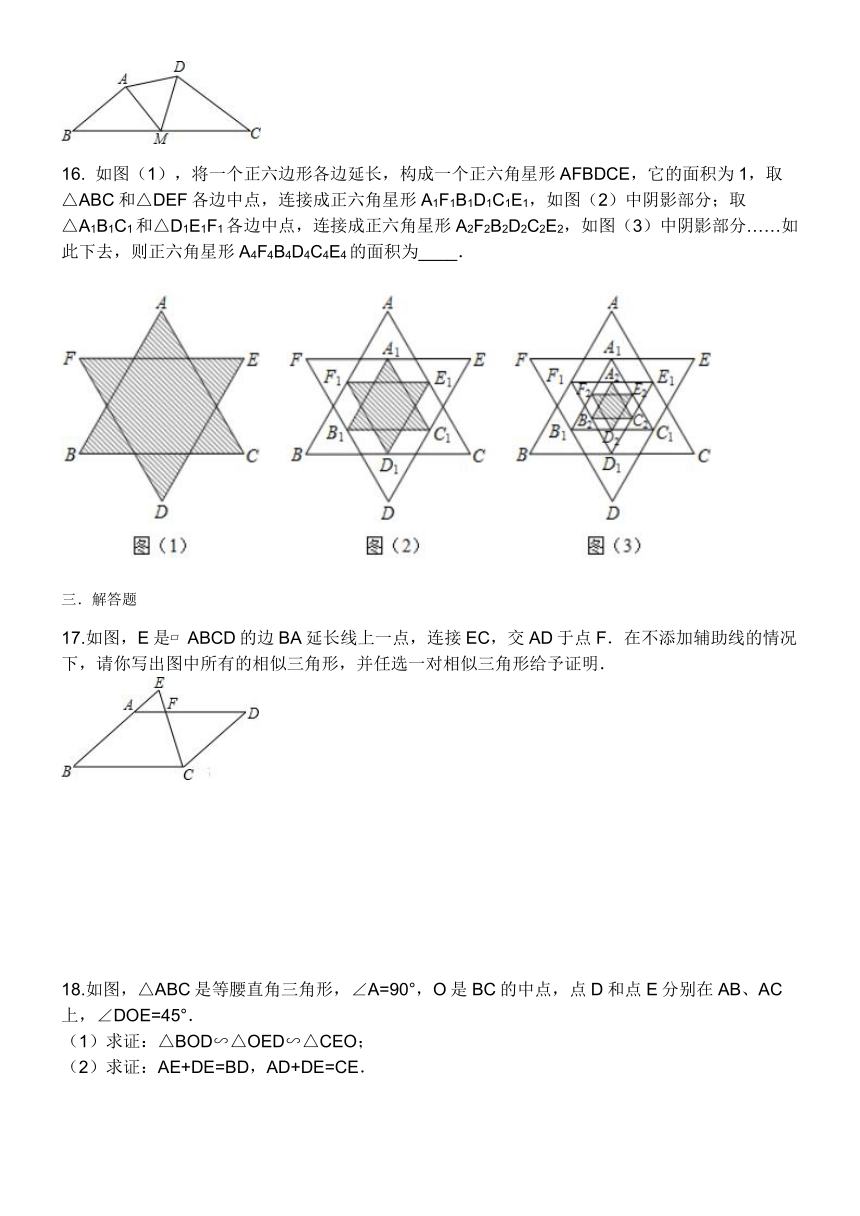
如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分……如此下去,则正六角星形A4F4B4D4C4E4的面积为____.
三.解答题
17.如图,E是?ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.
18.如图,△ABC是等腰直角三角形,∠A=90°,O是BC的中点,点D和点E分别在AB、AC上,∠DOE=45°.
(1)求证:△BOD∽△OED∽△CEO;
(2)求证:AE+DE=BD,AD+DE=CE.
19.小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
20.己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)当DF/FC=AD/DF时,求证:四边形BEFG是平行四边形.
21.如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)联结OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
22.已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°
(1)如图1,当四边形ABCD和EFCG均为正方形时,连接BF
①求证:△CAE∽△CBF;
②若BE=1,AE=2,求CE的长;
(2)如图2,当四边形ABCD和EFCG均为矩形,且==k时.若BE=1,AE=2,CE=3,则k=____.
参考答案
1.
--------------------------------------------------------------------------
【答案】利用平行线的性质和三角形外角等于和它不相邻的两个内角的和的性质就可求出.
∵AB∥CD,∴∠A=∠D=30°,再由三角形的外角的性质得,∠AOC=∠A+∠B=70°.
故选B.
2.
--------------------------------------------------------------------------
【解答】解:∵线段x是a,b的比例中项,
∴x2=ab,
即x2=36,
∴x=6(负数舍去),
故选A.
【分析】根据比例中项的定义可得x2=ab,从而易求x.
3.
--------------------------------------------------------------------------
C
4.
--------------------------------------------------------------------------
B
【解答】解:∵l1∥l2∥l3
,
∴
=
,即
=
,
解得,DE=
,
故选:B.
【分析】根据平行线分线段成比例定理得到比例式,求出DE的长.
5.
--------------------------------------------------------------------------
C
由DE∥FG∥BC,可得△ADE∽△AFG∽△ABC,又由AD:DF:FB=3:2:1,利用相似三角形的面积比等于相似比的平方,即可求得S
△ADE:S
△AFG:S
△ABC=9:25:36,然后设△ADE的面积是9a,则△AFG和△ABC的面积分别是25a,36a,即可求两个梯形的面积,继而求得答案.
解:∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∵AD:DF:FB=3:2:1,
∴AD:AF:AB=3:5:6,
∴S
△ADE:S
△AFG:S
△ABC=9:25:36,
设△ADE的面积是9a,则△AFG和△ABC的面积分别是25a,36a,
则S
四边形DFGE=S
△AFG-S
△ADE=16a,S
四边形FBCG=S
△ABC-S
△AFG=11a,
∴S
△ADE:S
四边形DFGE:S
四边形FBCG=9:16:11.
故选C.
6.
--------------------------------------------------------------------------
B.(-2m,-2n)
解:∵点A(-1,2)和点D(2,-4)是对应点,可得其位似比为1:2,
∴△ABC内的点P(m,n)的对应点P′的坐标为:(-2m,-2n).
故选:B.
直接利用位似图形的性质得出两图形的位似比进而得出答案.
7.
--------------------------------------------------------------------------
【解答】解:∵在Rt△ABC中,AB⊥AC,AB=3,AC=4,
∴由勾股定理得BC=5,
∵AB⊥AC,PE⊥AB,PD⊥AC,
∴PE∥AC,PD∥AB
∴△CDP∽△CAB,△BPE∽△BCA
∴,
∴PD=,PE=,
∴PD+PE=+=+3.
故选A.
【分析】先根据勾股定理求得BC的长,再根据相似三角形的判定得到△CDP∽△CAB,△BPE∽△BCA,利用相似三角形的边对应成比例就不难求得PD+PE了.
8.
--------------------------------------------------------------------------
A
9.
--------------------------------------------------------------------------
D
根据重心的概念得出D,F分别是三角形的中点.若设△ABC的面积是2,则△BCD的面积和△BCF的面积都是1.又因为BG:GF=CG:GD,可求得△CGF的面积.则四边形ADGF的面积也可求出.根据ASA可以证明△ADE≌△BDC,则△ADE的面积是1.则△AED的面积:四边形ADGF的面积可求.
解:设三角形ABC的面积是2
∴三角形BCD的面积和三角形BCF的面积都是1
∵BG:GF=CG:GD=2
∴三角形CGF的面积是
∴四边形ADGF的面积是2-1-
=
∵△ADE≌△BDC(ASA)
∴△ADE的面积是1
∴△AED的面积:四边形ADGF的面积=1:
=3:2.
故选D.
10.
--------------------------------------------------------------------------
B
【解答】①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=
x=BE,
∴EN=x,
∴CD=BD=DH+BH=(
+1)x,
即
=
+1,
∵EN∥DC,
∴△DCH∽△NEH,
∴
=
+1,即CH=(
+1)EH,正确;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而
,
∴
,
正确;
所以正确的只有②③.
故选B.
【分析】①如图,过H作HM⊥BC于M,根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;
②
设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三
角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用
对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用
相似三角形的性质即可结论②;
③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.此题比较复杂,综合性很强,主要考查了梯形的性质,相似三角形的判定和性质以及等腰直角三角形的性质.
11.
--------------------------------------------------------------------------
答案:2:3.
解:∵△ABC与△DEF相似比为2:3,
∴△ABC与△DEF对应边上中线的比为2:3.
【考点提示】
本题考查相似三角形,熟练掌握相似三角形的性质是解题关键;
【解题方法提示】
相似三角形的性质,相似三角形对应中线的比等于相似比;
根据相似三角形的相似比是2:3即可求出对应边上中线的比.
12.
--------------------------------------------------------------------------
答案为
13.
--------------------------------------------------------------------------
2
14.
--------------------------------------------------------------------------
解:∵AB=AC=1,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC=BD,
∵∠A=∠CBD,∠ACB=∠BCD,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=
AB=
.
故答案为
.
先根据等腰三角形的性质和三角形内角和计算出∠ABC=∠C=72°,再根据角平分线定义得到∠ABD=∠CBD=36°,易得AD=BC=BD,然后证明△ABC∽△BCD,利用相似得性质得AC:BC=BC:CD,则AC:AD=AD:CD,于是根据黄金分割点的定义得到点D为AC的黄金分割点,易得AD=
.
15.
--------------------------------------------------------------------------
解:∵∠BMD=∠BMA+∠AMD=∠C+∠CDM,
∵∠B=∠AMD=∠C=45°,
∴∠BMA=∠CDM,
∴△ABM∽△MCD,
∴=,
∵M为BC边的中点,
∴MC=BM,
∵AB=8,CD=9,
∴BM=MC=6,
∴BC=12,
延长BA与CD交于点E,
∵∠B=∠C=45°,
∴∠E=90°,BE=CE,
∴BE=CE=12,
∴AE=BE-AB=4,DE=CE-CD=3,
在Rt△AED中,AD=5.
故答案为5.
由∠BMD=∠BMA+∠AMD=∠C+∠CDM,∠B=∠AMD=∠C=45°,可证得△ABM∽△MCD,然后由相似三角形对应边成比例,求得MC与BM的值,然后延长BA与CD交于点E,由勾股定理,即可求得AD的长.
16.
--------------------------------------------------------------------------
答案:.
解:∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1DC1E1,且相似比为2:1,
∵正六角星形AFBDCE的面积为1,
∴正六角星形A1F1B1DC1E1的面积为,
同理可得,第二个六角星形的面积为:()2=,
第三个六角星形的面积为:()3=,
第四个六角星形的面积为:()4=.
1、认真观察题目,回想相似图形的判定与性质;
2、由A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,可得正六角星形AFBDCE∽正六角星形A1F1B1DC1E1,且相似比为2:1;
3、接下来,根据相似多边形的面积比等于相似比的平方即可求出正六角星形A1F1B1DC1E1的面积,同理可求出第二个、第三个、第四个六角星形的面积.
17.
--------------------------------------------------------------------------
【答案】根据平行线的性质和两角对应相等的两个三角形相似这一判定定理可证明图中相似三角形有:△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.
相似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.(3分)
如:△AEF∽△BEC.
在?ABCD中,AD∥BC,
∴∠1=∠B,∠2=∠3.(6分)
∴△AEF∽△BEC.(7分)
18.
--------------------------------------------------------------------------
【解答】证明:(1)∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BOD+∠BDO=180°,
∴∠BDO+∠BOD=135°,
∵∠EPF=45°,
又∵∠BOD+∠DOE+∠EOC=180°,
∴∠BOD+∠EOC=135°,
∴∠BOD=∠EOC,
又∵∠B=∠C,
∴△BOD∽△COE,
∴,
∵O是BC的中点,
∴,
∵∠B=∠DOE=45°,
∴△BOD∽△DOE,
∴△BOD∽△OED∽△CEO;
(2)连接AO,在AB上截取BF=AE,连接OF,
则AF=CE,
∵O是BC的中点,∠BAC=90°,AB=AC,
∴∠BAO=BAC=45°,AO=OC,
∴∠BAO=∠C,
在△AOF与△COE中,,
∴△AOF≌△COE,
∴OF=OE,∠AFO=∠CEO,
∵△BOD∽△DOE∽△COF,
∴∠EDO=∠FDO,∠CEO=∠DEO,
∴∠DEO=∠DFO,
在△DOF与△DOE中,,
∴△DOF≌△DOE,
∴DF=DE,
∵BD=BF+DF,
∴BD=AE+DE,
同理AD+DE=CE.
【分析】(1)由等腰直角三角形的性质得∠B=∠C=45°.根据三角形的内角和和平角的定义得到∠BOD=∠EOC,推出△BOD∽△COE,根据相似三角形的性质得到,等量代换得到,于是得到结论;
(2)连接AO,在AB上截取BF=AE,连接OF,则AF=CE,根据等腰直角三角形的性质得到∠BAO=∠C,根据全等三角形的性质得到OF=OE,∠AFO=∠CEO,根据相似三角形的性质得到∠DEO=∠DFO,推出△DOF≌△DOE,根据全等三角形的性质得到DF=DE,于是得到结论.
19.
--------------------------------------------------------------------------
解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDF,
设AB=x,BC=y
∴
,
解得
.经检验
""是此方程组的解。
答;这棵古松的高约为10.2米
【分析】这是一道实际问题,首先要将实际问题转化为数学问题。根据反射定律可以得到∠ACB=∠ECF,∠ADB=∠GDH,题中隐含了AB⊥BC,EF⊥BC,GH⊥BC,由此可证得△BAC∽△FEC、△ADB∽△GDF,根据相似三角形的性质建立方程组,求出方程组的解即可。
20.
--------------------------------------------------------------------------
证明:(1)∵四边形ABCD是菱形,
∴AB=AD,∠ABC=∠ADF,
∵∠BAF=∠DAE,
∴∠BAF-∠EAF=∠DAE-∠EAF,
即:∠BAE=∠DAF,
∴△BAE≌△DAF
∴BE=DF;
(2)∵四边形ABCD是菱形,
∴AD∥BC,
∴△ADG∽△EBG
∴ADBE=DGBG
又∵BE=DF,DFFC=ADDF
∴DGBG=ADDF=DFFC
∴GF∥BC
(平行线分线段成比例)
∴∠DGF=∠DBC
∵BC=CD
∴∠BDC=∠DBC=∠DGF
∴GF=DF=BE
∵GF∥BC,GF=BE
∴四边形BEFG是平行四边形
(1)证得△ABE与△AFD全等后即可证得结论;
(2))利用DFFC=ADDF得到FDFC=ADBE=DGGB,从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,最后证得BE=GF,利用一组对边平行且相等即可判定平行四边形.
21.
--------------------------------------------------------------------------
【解答】解:(1)如图,过点A作AD⊥y轴于点D,
∵AO=OB=4,
∴B(4,0).
∵∠AOB=120°,
∴∠AOD=30°,
∴AD=OA=2,OD=OA=2.
∴A(-2,2).
将A(-2,2),B(4,0)代入y=ax2+bx,得:
,解得:,
∴这条抛物线的表达式为y=x2-x;
(2)过点M作ME⊥x轴于点E,
∵y=x2-x=(x-2)2-,
∴M(2,-),即OE=2,EM=.
∴tan∠EOM==.
∴∠EOM=30°.
∴∠AOM=∠AOB+∠EOM=150°.
(3)过点A作AH⊥x轴于点H,
∵AH=2,HB=HO+OB=6,
∴tan∠ABH==.
∴∠ABH=30°,
∵∠AOM=150°,
∴∠OAM<30°,
∴∠OMA<30°,
∴点C不可能在点B的左侧,只能在点B的右侧.
∴∠ABC=180°-∠ABH=150°,
∵∠AOM=150°,
∴∠AOM=∠ABC.
∴△ABC与△AOM相似,有如下两种可能:
①△BAC与∽△OAM,②△BAC与∽△OMA
∵OD=2,ME=,
∴OM=,
∵AH=2,BH=6,
∴AB=4.
①当△BAC与∽△OAM时,
由=得,解得BC=4.
∴C1(8,0).
②当△BAC与∽△OMA时,
由=得,解得BC=12.
∴C2(16,0).
综上所述,如果点C在x轴上,且△ABC与△AOM相似,
则点C的坐标为(8,0)或(16,0).
【分析】(1)过点A作AD⊥y轴于点D,由已知易得∠AOD=30°,B(4,0),解直角三角形求得AD=2,OD=2,从而求得A点的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)过点M作ME⊥x轴于点E,先求得顶点M的坐标,然后根据tan∠EOM==.求得∠EOM=30°,即可求得∠AOM=∠AOB+∠EOM=150°.
(3)过点A作AH⊥x轴于点H,求得∠ABH=30°,根据∠AOM=150°,判断∠OAM<30°,∠OMA<30°,从而判定点C不可能在点B的左侧,只能在点B的右侧,易证得∠AOM=∠ABC.所以△ABC与△AOM相似,有两种可能:①△BAC与∽△OAM,②△BAC与∽△OMA,然后分两种情况分别讨论即可求得.
22.
--------------------------------------------------------------------------
(1)证明:
①∵四边形ABCD和EFCG均为正方形,
∴==,
∵∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF;
②∵△CAE∽△CBF,
∴∠CBF=∠CAE,=,
∵AE=2,
∴BF=,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
在Rt△EBF中,EF==,
∵四边形EFCG为正方形,
∴CE=EF=;
(3)连接BF,
∵=,∠ABC=∠EFC=90°,
∴Rt△ABC∽Rt△CEF,
∴=,
又∠ACB=∠ECF,
∴∠ACE=∠BCF,
∴△ACE∽△BCF,
∴==,
∵AE=2,
∴BF=,
∵∠EBF=90°,
∴EF2=BE2+BF2=1+,
∵CE=EF,
∴CE2=(1+)(1+)=9,解得k=或k=-(不合题意,舍去),
故答案为:.
(1)①首先根据四边形ABCD和EFCG均为正方形,可得==,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
②首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
(2)首先根据相似三角形判定的方法,判断出△ACE∽△BCF,即可判断出==,据此求出BF的长度是多少;然后判断出∠EBF=90°,在Rt△BEF中,根据勾股定理,求出EF的值是多少,进而求出k的值是多少即可.
相似三角形综合测试卷
一.选择题
1.如图,已知AD与BC相交于点O,AB∥CD,如果∠B=40°,∠D=30°,则∠AOC=(
)
A.
60°
B.
70°
C.
80°
D.
120°
2.已知线段a=4,b=9,线段x是a,b的比例中项,则x等于( )
A.
6
B.
6或-6
C.
-6
D.
36
3.如图,A﹑B两点分别位于一个池塘的两端,小明想用绳子测量A﹑B间的距离,但绳子不够,于是他想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,在AC的延长线上取一点D,使CD=CA,在BC的延长线上取一点E,使CE=CB,测得DE的长为5米,则AB两点间的距离为( )
A.
6米
B.
8米
C.
10米
D.
12米
4.如图,直线l
1∥l2∥l3
,
直线AC分别交l1
,
l2
,
l3于点A,B,C,直线DF分别交l1
,
l2
,
l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是(??????)
A.
3
B.
C.
D.
5.如图,在△ABC中,DE∥FG∥BC,AD:DF:FB=3:2:1,则△ADE,四边形DFGE,四边形FBCG的面积比为( )
A.
3:2:1
B.
9:4:1
C.
9:16:11
D.
9:25:36
6.如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
A.
(2m,2n)
B.
(-2m,-2n)
C.
(2m,-2n)
D.
(-2m,2n)
7.如图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=( )
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC=√5,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为(
).
A.
B.
C.
D.
9.如图,G是△ABC的重心,直线L过A点与BC平行.若直线CG分别与AB,L交于D,E两点,直线BG与AC交于F点,则△AED的面积:四边形ADGF的面积=( )
A.
1:2
B.
2:1
C.
2:3
D.
3:2
10.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=;③
.
其中正确的是( )
A.
①②
B.
②③
C.
①③
D.
①②③
二.填空题
11.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为____.
12.已知,则
13.如图,E为ABCD的边AD延长线上一点,且D为AE的黄金分割点,即AD=AE,BE交DC于点F,已知AB=+1,则CF的长是________.
14.顶角是36°的等腰三角形称为黄金三角形,如图,在△ABC中,AB=AC=1,∠A=36°,BD是△ABC的角平分线,那么AD=
.
15.如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为____
16.
如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分……如此下去,则正六角星形A4F4B4D4C4E4的面积为____.
三.解答题
17.如图,E是?ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.
18.如图,△ABC是等腰直角三角形,∠A=90°,O是BC的中点,点D和点E分别在AB、AC上,∠DOE=45°.
(1)求证:△BOD∽△OED∽△CEO;
(2)求证:AE+DE=BD,AD+DE=CE.
19.小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
20.己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)当DF/FC=AD/DF时,求证:四边形BEFG是平行四边形.
21.如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)联结OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
22.已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°
(1)如图1,当四边形ABCD和EFCG均为正方形时,连接BF
①求证:△CAE∽△CBF;
②若BE=1,AE=2,求CE的长;
(2)如图2,当四边形ABCD和EFCG均为矩形,且==k时.若BE=1,AE=2,CE=3,则k=____.
参考答案
1.
--------------------------------------------------------------------------
【答案】利用平行线的性质和三角形外角等于和它不相邻的两个内角的和的性质就可求出.
∵AB∥CD,∴∠A=∠D=30°,再由三角形的外角的性质得,∠AOC=∠A+∠B=70°.
故选B.
2.
--------------------------------------------------------------------------
【解答】解:∵线段x是a,b的比例中项,
∴x2=ab,
即x2=36,
∴x=6(负数舍去),
故选A.
【分析】根据比例中项的定义可得x2=ab,从而易求x.
3.
--------------------------------------------------------------------------
C
4.
--------------------------------------------------------------------------
B
【解答】解:∵l1∥l2∥l3
,
∴
=
,即
=
,
解得,DE=
,
故选:B.
【分析】根据平行线分线段成比例定理得到比例式,求出DE的长.
5.
--------------------------------------------------------------------------
C
由DE∥FG∥BC,可得△ADE∽△AFG∽△ABC,又由AD:DF:FB=3:2:1,利用相似三角形的面积比等于相似比的平方,即可求得S
△ADE:S
△AFG:S
△ABC=9:25:36,然后设△ADE的面积是9a,则△AFG和△ABC的面积分别是25a,36a,即可求两个梯形的面积,继而求得答案.
解:∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∵AD:DF:FB=3:2:1,
∴AD:AF:AB=3:5:6,
∴S
△ADE:S
△AFG:S
△ABC=9:25:36,
设△ADE的面积是9a,则△AFG和△ABC的面积分别是25a,36a,
则S
四边形DFGE=S
△AFG-S
△ADE=16a,S
四边形FBCG=S
△ABC-S
△AFG=11a,
∴S
△ADE:S
四边形DFGE:S
四边形FBCG=9:16:11.
故选C.
6.
--------------------------------------------------------------------------
B.(-2m,-2n)
解:∵点A(-1,2)和点D(2,-4)是对应点,可得其位似比为1:2,
∴△ABC内的点P(m,n)的对应点P′的坐标为:(-2m,-2n).
故选:B.
直接利用位似图形的性质得出两图形的位似比进而得出答案.
7.
--------------------------------------------------------------------------
【解答】解:∵在Rt△ABC中,AB⊥AC,AB=3,AC=4,
∴由勾股定理得BC=5,
∵AB⊥AC,PE⊥AB,PD⊥AC,
∴PE∥AC,PD∥AB
∴△CDP∽△CAB,△BPE∽△BCA
∴,
∴PD=,PE=,
∴PD+PE=+=+3.
故选A.
【分析】先根据勾股定理求得BC的长,再根据相似三角形的判定得到△CDP∽△CAB,△BPE∽△BCA,利用相似三角形的边对应成比例就不难求得PD+PE了.
8.
--------------------------------------------------------------------------
A
9.
--------------------------------------------------------------------------
D
根据重心的概念得出D,F分别是三角形的中点.若设△ABC的面积是2,则△BCD的面积和△BCF的面积都是1.又因为BG:GF=CG:GD,可求得△CGF的面积.则四边形ADGF的面积也可求出.根据ASA可以证明△ADE≌△BDC,则△ADE的面积是1.则△AED的面积:四边形ADGF的面积可求.
解:设三角形ABC的面积是2
∴三角形BCD的面积和三角形BCF的面积都是1
∵BG:GF=CG:GD=2
∴三角形CGF的面积是
∴四边形ADGF的面积是2-1-
=
∵△ADE≌△BDC(ASA)
∴△ADE的面积是1
∴△AED的面积:四边形ADGF的面积=1:
=3:2.
故选D.
10.
--------------------------------------------------------------------------
B
【解答】①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=
x=BE,
∴EN=x,
∴CD=BD=DH+BH=(
+1)x,
即
=
+1,
∵EN∥DC,
∴△DCH∽△NEH,
∴
=
+1,即CH=(
+1)EH,正确;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而
,
∴
,
正确;
所以正确的只有②③.
故选B.
【分析】①如图,过H作HM⊥BC于M,根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;
②
设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三
角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用
对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用
相似三角形的性质即可结论②;
③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.此题比较复杂,综合性很强,主要考查了梯形的性质,相似三角形的判定和性质以及等腰直角三角形的性质.
11.
--------------------------------------------------------------------------
答案:2:3.
解:∵△ABC与△DEF相似比为2:3,
∴△ABC与△DEF对应边上中线的比为2:3.
【考点提示】
本题考查相似三角形,熟练掌握相似三角形的性质是解题关键;
【解题方法提示】
相似三角形的性质,相似三角形对应中线的比等于相似比;
根据相似三角形的相似比是2:3即可求出对应边上中线的比.
12.
--------------------------------------------------------------------------
答案为
13.
--------------------------------------------------------------------------
2
14.
--------------------------------------------------------------------------
解:∵AB=AC=1,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC=BD,
∵∠A=∠CBD,∠ACB=∠BCD,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=
AB=
.
故答案为
.
先根据等腰三角形的性质和三角形内角和计算出∠ABC=∠C=72°,再根据角平分线定义得到∠ABD=∠CBD=36°,易得AD=BC=BD,然后证明△ABC∽△BCD,利用相似得性质得AC:BC=BC:CD,则AC:AD=AD:CD,于是根据黄金分割点的定义得到点D为AC的黄金分割点,易得AD=
.
15.
--------------------------------------------------------------------------
解:∵∠BMD=∠BMA+∠AMD=∠C+∠CDM,
∵∠B=∠AMD=∠C=45°,
∴∠BMA=∠CDM,
∴△ABM∽△MCD,
∴=,
∵M为BC边的中点,
∴MC=BM,
∵AB=8,CD=9,
∴BM=MC=6,
∴BC=12,
延长BA与CD交于点E,
∵∠B=∠C=45°,
∴∠E=90°,BE=CE,
∴BE=CE=12,
∴AE=BE-AB=4,DE=CE-CD=3,
在Rt△AED中,AD=5.
故答案为5.
由∠BMD=∠BMA+∠AMD=∠C+∠CDM,∠B=∠AMD=∠C=45°,可证得△ABM∽△MCD,然后由相似三角形对应边成比例,求得MC与BM的值,然后延长BA与CD交于点E,由勾股定理,即可求得AD的长.
16.
--------------------------------------------------------------------------
答案:.
解:∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1DC1E1,且相似比为2:1,
∵正六角星形AFBDCE的面积为1,
∴正六角星形A1F1B1DC1E1的面积为,
同理可得,第二个六角星形的面积为:()2=,
第三个六角星形的面积为:()3=,
第四个六角星形的面积为:()4=.
1、认真观察题目,回想相似图形的判定与性质;
2、由A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,可得正六角星形AFBDCE∽正六角星形A1F1B1DC1E1,且相似比为2:1;
3、接下来,根据相似多边形的面积比等于相似比的平方即可求出正六角星形A1F1B1DC1E1的面积,同理可求出第二个、第三个、第四个六角星形的面积.
17.
--------------------------------------------------------------------------
【答案】根据平行线的性质和两角对应相等的两个三角形相似这一判定定理可证明图中相似三角形有:△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.
相似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.(3分)
如:△AEF∽△BEC.
在?ABCD中,AD∥BC,
∴∠1=∠B,∠2=∠3.(6分)
∴△AEF∽△BEC.(7分)
18.
--------------------------------------------------------------------------
【解答】证明:(1)∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BOD+∠BDO=180°,
∴∠BDO+∠BOD=135°,
∵∠EPF=45°,
又∵∠BOD+∠DOE+∠EOC=180°,
∴∠BOD+∠EOC=135°,
∴∠BOD=∠EOC,
又∵∠B=∠C,
∴△BOD∽△COE,
∴,
∵O是BC的中点,
∴,
∵∠B=∠DOE=45°,
∴△BOD∽△DOE,
∴△BOD∽△OED∽△CEO;
(2)连接AO,在AB上截取BF=AE,连接OF,
则AF=CE,
∵O是BC的中点,∠BAC=90°,AB=AC,
∴∠BAO=BAC=45°,AO=OC,
∴∠BAO=∠C,
在△AOF与△COE中,,
∴△AOF≌△COE,
∴OF=OE,∠AFO=∠CEO,
∵△BOD∽△DOE∽△COF,
∴∠EDO=∠FDO,∠CEO=∠DEO,
∴∠DEO=∠DFO,
在△DOF与△DOE中,,
∴△DOF≌△DOE,
∴DF=DE,
∵BD=BF+DF,
∴BD=AE+DE,
同理AD+DE=CE.
【分析】(1)由等腰直角三角形的性质得∠B=∠C=45°.根据三角形的内角和和平角的定义得到∠BOD=∠EOC,推出△BOD∽△COE,根据相似三角形的性质得到,等量代换得到,于是得到结论;
(2)连接AO,在AB上截取BF=AE,连接OF,则AF=CE,根据等腰直角三角形的性质得到∠BAO=∠C,根据全等三角形的性质得到OF=OE,∠AFO=∠CEO,根据相似三角形的性质得到∠DEO=∠DFO,推出△DOF≌△DOE,根据全等三角形的性质得到DF=DE,于是得到结论.
19.
--------------------------------------------------------------------------
解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDF,
设AB=x,BC=y
∴
,
解得
.经检验
""是此方程组的解。
答;这棵古松的高约为10.2米
【分析】这是一道实际问题,首先要将实际问题转化为数学问题。根据反射定律可以得到∠ACB=∠ECF,∠ADB=∠GDH,题中隐含了AB⊥BC,EF⊥BC,GH⊥BC,由此可证得△BAC∽△FEC、△ADB∽△GDF,根据相似三角形的性质建立方程组,求出方程组的解即可。
20.
--------------------------------------------------------------------------
证明:(1)∵四边形ABCD是菱形,
∴AB=AD,∠ABC=∠ADF,
∵∠BAF=∠DAE,
∴∠BAF-∠EAF=∠DAE-∠EAF,
即:∠BAE=∠DAF,
∴△BAE≌△DAF
∴BE=DF;
(2)∵四边形ABCD是菱形,
∴AD∥BC,
∴△ADG∽△EBG
∴ADBE=DGBG
又∵BE=DF,DFFC=ADDF
∴DGBG=ADDF=DFFC
∴GF∥BC
(平行线分线段成比例)
∴∠DGF=∠DBC
∵BC=CD
∴∠BDC=∠DBC=∠DGF
∴GF=DF=BE
∵GF∥BC,GF=BE
∴四边形BEFG是平行四边形
(1)证得△ABE与△AFD全等后即可证得结论;
(2))利用DFFC=ADDF得到FDFC=ADBE=DGGB,从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,最后证得BE=GF,利用一组对边平行且相等即可判定平行四边形.
21.
--------------------------------------------------------------------------
【解答】解:(1)如图,过点A作AD⊥y轴于点D,
∵AO=OB=4,
∴B(4,0).
∵∠AOB=120°,
∴∠AOD=30°,
∴AD=OA=2,OD=OA=2.
∴A(-2,2).
将A(-2,2),B(4,0)代入y=ax2+bx,得:
,解得:,
∴这条抛物线的表达式为y=x2-x;
(2)过点M作ME⊥x轴于点E,
∵y=x2-x=(x-2)2-,
∴M(2,-),即OE=2,EM=.
∴tan∠EOM==.
∴∠EOM=30°.
∴∠AOM=∠AOB+∠EOM=150°.
(3)过点A作AH⊥x轴于点H,
∵AH=2,HB=HO+OB=6,
∴tan∠ABH==.
∴∠ABH=30°,
∵∠AOM=150°,
∴∠OAM<30°,
∴∠OMA<30°,
∴点C不可能在点B的左侧,只能在点B的右侧.
∴∠ABC=180°-∠ABH=150°,
∵∠AOM=150°,
∴∠AOM=∠ABC.
∴△ABC与△AOM相似,有如下两种可能:
①△BAC与∽△OAM,②△BAC与∽△OMA
∵OD=2,ME=,
∴OM=,
∵AH=2,BH=6,
∴AB=4.
①当△BAC与∽△OAM时,
由=得,解得BC=4.
∴C1(8,0).
②当△BAC与∽△OMA时,
由=得,解得BC=12.
∴C2(16,0).
综上所述,如果点C在x轴上,且△ABC与△AOM相似,
则点C的坐标为(8,0)或(16,0).
【分析】(1)过点A作AD⊥y轴于点D,由已知易得∠AOD=30°,B(4,0),解直角三角形求得AD=2,OD=2,从而求得A点的坐标,然后根据待定系数法即可求得抛物线的解析式;
(2)过点M作ME⊥x轴于点E,先求得顶点M的坐标,然后根据tan∠EOM==.求得∠EOM=30°,即可求得∠AOM=∠AOB+∠EOM=150°.
(3)过点A作AH⊥x轴于点H,求得∠ABH=30°,根据∠AOM=150°,判断∠OAM<30°,∠OMA<30°,从而判定点C不可能在点B的左侧,只能在点B的右侧,易证得∠AOM=∠ABC.所以△ABC与△AOM相似,有两种可能:①△BAC与∽△OAM,②△BAC与∽△OMA,然后分两种情况分别讨论即可求得.
22.
--------------------------------------------------------------------------
(1)证明:
①∵四边形ABCD和EFCG均为正方形,
∴==,
∵∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF;
②∵△CAE∽△CBF,
∴∠CBF=∠CAE,=,
∵AE=2,
∴BF=,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
在Rt△EBF中,EF==,
∵四边形EFCG为正方形,
∴CE=EF=;
(3)连接BF,
∵=,∠ABC=∠EFC=90°,
∴Rt△ABC∽Rt△CEF,
∴=,
又∠ACB=∠ECF,
∴∠ACE=∠BCF,
∴△ACE∽△BCF,
∴==,
∵AE=2,
∴BF=,
∵∠EBF=90°,
∴EF2=BE2+BF2=1+,
∵CE=EF,
∴CE2=(1+)(1+)=9,解得k=或k=-(不合题意,舍去),
故答案为:.
(1)①首先根据四边形ABCD和EFCG均为正方形,可得==,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
②首先根据△CAE∽△CBF,判断出∠CAE=∠CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
(2)首先根据相似三角形判定的方法,判断出△ACE∽△BCF,即可判断出==,据此求出BF的长度是多少;然后判断出∠EBF=90°,在Rt△BEF中,根据勾股定理,求出EF的值是多少,进而求出k的值是多少即可.
同课章节目录
