2.5有理数的乘方(1) 教学课件(共23张PPT)
文档属性
| 名称 | 2.5有理数的乘方(1) 教学课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览








文档简介
有理数的乘方一
1.除法法则:
两个有理数相除, 同号得正, 异号得负,并把绝对值相除;0除以任何非0数都得0.
2.除法和乘法之间的关系:
除以一个数, 等于乘以这个数的倒数.
知识回顾
假设一张厚度为0.09mm的纸连续对折始终是可能的,对折多少次后,所得的厚度将超过你的身高?
新课导入
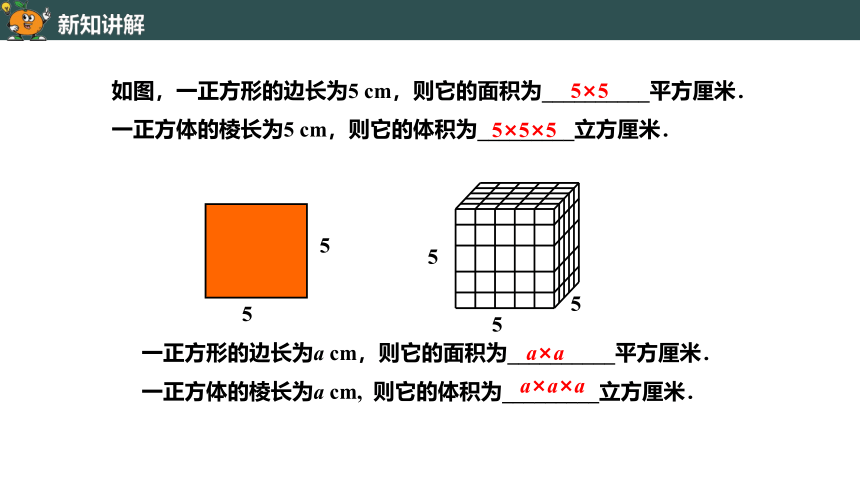
如图,一正方形的边长为5 cm,则它的面积为__________平方厘米.
一正方体的棱长为5 cm,则它的体积为_________立方厘米.
5
5
5
5
5
5×5
5×5×5
一正方形的边长为a cm,则它的面积为__________平方厘米.
一正方体的棱长为a cm, 则它的体积为_________立方厘米.
a×a×a
a×a
新知讲解
5×5记作52,读作:5的平方(5的二次方);
5×5×5记作53,读作:5的立方(5的三次方).
类似地,5×5×5×5记作_________;
5×5×5 ×5×5记作_________;
记作_________ .
5×5×???×5
n个5
54
55
5n
a×a记作_________;
a×a×a记作_________;
记作_________.
a×a ×… ×a ×a
n个a
a2
a3
an
新知讲解
这种求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
an
幂
指数
(因数的个数)
底数
(相同因数)
an读做“ a的n次方”,或读做“a的n次幂”.
新知讲解
(1)一个数可以看作这个数的本身的一次方.
(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.
(3)分数的乘方,在书写的时候也一定要把整个分数用小括号括起来.
注意
1.把下列相同因数的乘积写成幂的形式,并说出底数和指数.
(1)(-6)×(-6) ×(-6);
(2) ;
写为 ,底数是 ,指数是4;
2.把 写成几个相同因数相乘的形式.
解: .
写为(-6)3,底数是-6,指数是3;
写为(-2)10,底数是-2,指数是10.
做一做
说说下列各数的意义,它们一样吗?
43,42,4×2.
43表示3个4相乘;42表示2个4相乘;3×4表示3个4相加.
(-3)4和-34.
(-3)4的意义是-3的4次方,即4个-3相乘;
-34的意义是4的4次方的相反数.
和 .
的意义是 的平方,即2个 相乘;
的意义是“2的平方再除以3”.
巩固练习
例1 计算:
(1) (-3)2;(2)1.53;(3) ;(4) (-1)11.
解:(1) (-3)2=(-3)×(-3)=9;
(2)1.53=1.5×1.5×1.5=3.375;
(3)
;
(4) .
例题讲解
计算:
(1)73; (2)(-3)4; (3) ; (4) ;(5)1.52.
解:(1)73=7×7×7=343
(2)(-2)4=(-2)× (-2) × (-2) × (-2) =16
(3)
(4)
(5)2.62=2.6 × 2.6=6.76
变式训练
计算:
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1000
=10000
=100
=-1000
=10000
观察上面的计算的结果,你能发现什么规律?
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
做一做
例2 计算:
(1) -32 ; (2)3×23; (3)(3×2)3;(4)8÷(-2)3.
解:(1) -32 =-(3×3)=-9;
(2)3×23=3×8=24;
(3)(3×2)3=63=216;
(4)8÷(-2)3= 8÷ (-8)=-1.
有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
例题讲解
计算:
(1)8×23; (2)(5×2)3;
(3)(-2)2×(-3)2; (4)(-2)3÷22.
解:(1)8×23=8×8=64;
(2)(2×5)3=103=1000;
(3)(-4)2×(-3)2=16 × 9=144;
(4)(-2)4÷22 =(-16)÷4=-4.
变式训练
1.计算(﹣1)2017的结果是( )
A.﹣1 B.1 C.﹣2017 D.2017
解:(﹣1)2017=﹣1,
故选A.
课后练习
2.若a=﹣2×32,b=(﹣2×3)2,c=﹣(2×3)2,则下列大小关系中正确的是( )
A.a>b>c B.b>c>a C.b>a>c D.c>a>b
【分析】分别计算出各数,再根据有理数比较大小的法则进行比较即可.
解:∵a=﹣2×32=﹣2×9=﹣18,b=(﹣2×3)2=36,
c=﹣(2×3)2=﹣36,
又∵36>﹣18>﹣36,
∴b>a>c.故选C.
课后练习
3.如果n是正整数,那么n[1﹣(﹣1)n]的值( )
A.一定是零 B.一定是偶数 C.一定是奇数 D.是零或偶数
【分析】分为两种情况当n是偶数时,当n是奇数时,求出即可.
解:当n是偶数时,原式=n[1﹣1]=0,
当n是奇数时,原式=n[1+1]=2n,是偶数;
故选D.
课后练习
4、35 表示 ( )
A . 3个5相乘 B . 5个3相乘
C . 5与3的积 D. 5个3相加的和
5、计算(-1)5的值等于( )
A.-1 B.1 C.-2 D.2
6、对于乘积(-2)×(-2)×(-2)×(-2),记法正确的是( )
A.-24 B.-(+2)4 C.(-2)4 D.(-2)×4
B
A
C
课后练习
7.某种细胞每过30分钟便由1个分裂成2个.请根据你所学的知识,计算1天(24小时)后1个细胞可以分裂成多少个细胞.
解:根据题意得:1天(24小时)后1个细胞可以分裂成248个细胞.
课后练习
8.2011年3月11日,日本大地震引发福岛核电站核泄漏,其中一种主要放射性元素是碘131,这种物质会不断蜕变为其他物质,平均每经过1天剩留的物质约为原来的91.7%.问3天后剩留的物质是原来的百分之几(精确到0.1%)?
(91.7%)?≈77.1%.
课后练习
1.有理数的乘方:求几个相同因数的积的运算叫做乘方.
2.幂的性质:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.0的任何正整数次幂都为0.
3 .有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
课后小结
教材练习题
课后作业
谢
谢
观
看
1.除法法则:
两个有理数相除, 同号得正, 异号得负,并把绝对值相除;0除以任何非0数都得0.
2.除法和乘法之间的关系:
除以一个数, 等于乘以这个数的倒数.
知识回顾
假设一张厚度为0.09mm的纸连续对折始终是可能的,对折多少次后,所得的厚度将超过你的身高?
新课导入
如图,一正方形的边长为5 cm,则它的面积为__________平方厘米.
一正方体的棱长为5 cm,则它的体积为_________立方厘米.
5
5
5
5
5
5×5
5×5×5
一正方形的边长为a cm,则它的面积为__________平方厘米.
一正方体的棱长为a cm, 则它的体积为_________立方厘米.
a×a×a
a×a
新知讲解
5×5记作52,读作:5的平方(5的二次方);
5×5×5记作53,读作:5的立方(5的三次方).
类似地,5×5×5×5记作_________;
5×5×5 ×5×5记作_________;
记作_________ .
5×5×???×5
n个5
54
55
5n
a×a记作_________;
a×a×a记作_________;
记作_________.
a×a ×… ×a ×a
n个a
a2
a3
an
新知讲解
这种求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
an
幂
指数
(因数的个数)
底数
(相同因数)
an读做“ a的n次方”,或读做“a的n次幂”.
新知讲解
(1)一个数可以看作这个数的本身的一次方.
(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.
(3)分数的乘方,在书写的时候也一定要把整个分数用小括号括起来.
注意
1.把下列相同因数的乘积写成幂的形式,并说出底数和指数.
(1)(-6)×(-6) ×(-6);
(2) ;
写为 ,底数是 ,指数是4;
2.把 写成几个相同因数相乘的形式.
解: .
写为(-6)3,底数是-6,指数是3;
写为(-2)10,底数是-2,指数是10.
做一做
说说下列各数的意义,它们一样吗?
43,42,4×2.
43表示3个4相乘;42表示2个4相乘;3×4表示3个4相加.
(-3)4和-34.
(-3)4的意义是-3的4次方,即4个-3相乘;
-34的意义是4的4次方的相反数.
和 .
的意义是 的平方,即2个 相乘;
的意义是“2的平方再除以3”.
巩固练习
例1 计算:
(1) (-3)2;(2)1.53;(3) ;(4) (-1)11.
解:(1) (-3)2=(-3)×(-3)=9;
(2)1.53=1.5×1.5×1.5=3.375;
(3)
;
(4) .
例题讲解
计算:
(1)73; (2)(-3)4; (3) ; (4) ;(5)1.52.
解:(1)73=7×7×7=343
(2)(-2)4=(-2)× (-2) × (-2) × (-2) =16
(3)
(4)
(5)2.62=2.6 × 2.6=6.76
变式训练
计算:
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1000
=10000
=100
=-1000
=10000
观察上面的计算的结果,你能发现什么规律?
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
做一做
例2 计算:
(1) -32 ; (2)3×23; (3)(3×2)3;(4)8÷(-2)3.
解:(1) -32 =-(3×3)=-9;
(2)3×23=3×8=24;
(3)(3×2)3=63=216;
(4)8÷(-2)3= 8÷ (-8)=-1.
有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
例题讲解
计算:
(1)8×23; (2)(5×2)3;
(3)(-2)2×(-3)2; (4)(-2)3÷22.
解:(1)8×23=8×8=64;
(2)(2×5)3=103=1000;
(3)(-4)2×(-3)2=16 × 9=144;
(4)(-2)4÷22 =(-16)÷4=-4.
变式训练
1.计算(﹣1)2017的结果是( )
A.﹣1 B.1 C.﹣2017 D.2017
解:(﹣1)2017=﹣1,
故选A.
课后练习
2.若a=﹣2×32,b=(﹣2×3)2,c=﹣(2×3)2,则下列大小关系中正确的是( )
A.a>b>c B.b>c>a C.b>a>c D.c>a>b
【分析】分别计算出各数,再根据有理数比较大小的法则进行比较即可.
解:∵a=﹣2×32=﹣2×9=﹣18,b=(﹣2×3)2=36,
c=﹣(2×3)2=﹣36,
又∵36>﹣18>﹣36,
∴b>a>c.故选C.
课后练习
3.如果n是正整数,那么n[1﹣(﹣1)n]的值( )
A.一定是零 B.一定是偶数 C.一定是奇数 D.是零或偶数
【分析】分为两种情况当n是偶数时,当n是奇数时,求出即可.
解:当n是偶数时,原式=n[1﹣1]=0,
当n是奇数时,原式=n[1+1]=2n,是偶数;
故选D.
课后练习
4、35 表示 ( )
A . 3个5相乘 B . 5个3相乘
C . 5与3的积 D. 5个3相加的和
5、计算(-1)5的值等于( )
A.-1 B.1 C.-2 D.2
6、对于乘积(-2)×(-2)×(-2)×(-2),记法正确的是( )
A.-24 B.-(+2)4 C.(-2)4 D.(-2)×4
B
A
C
课后练习
7.某种细胞每过30分钟便由1个分裂成2个.请根据你所学的知识,计算1天(24小时)后1个细胞可以分裂成多少个细胞.
解:根据题意得:1天(24小时)后1个细胞可以分裂成248个细胞.
课后练习
8.2011年3月11日,日本大地震引发福岛核电站核泄漏,其中一种主要放射性元素是碘131,这种物质会不断蜕变为其他物质,平均每经过1天剩留的物质约为原来的91.7%.问3天后剩留的物质是原来的百分之几(精确到0.1%)?
(91.7%)?≈77.1%.
课后练习
1.有理数的乘方:求几个相同因数的积的运算叫做乘方.
2.幂的性质:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.0的任何正整数次幂都为0.
3 .有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
课后小结
教材练习题
课后作业
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
