2.5有理数的乘方(2) 教学课件(共16张PPT)
文档属性
| 名称 | 2.5有理数的乘方(2) 教学课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览






文档简介
有理数的乘方二
1.有理数的乘方:求几个相同因数的积的运算叫做乘方.
2.幂的性质:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.0的任何正整数次幂都为0.
3 .有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
知识回顾
情境一:2003年10月15日,中国首次进行载人航天飞行,飞船绕地球飞行了14圈,行程约60万 km,已知赤道长度约40000 km,飞船行程相当于多少个赤道长?
情境二:如果某市每人每天节约用水0.5千克,该市约有1千3百万人口,那么该市每天节约用水多少千克?
在日常的生产和生活中,我们经常遇到一些较大的数,怎样使较大的数读写方便呢?
导入新课
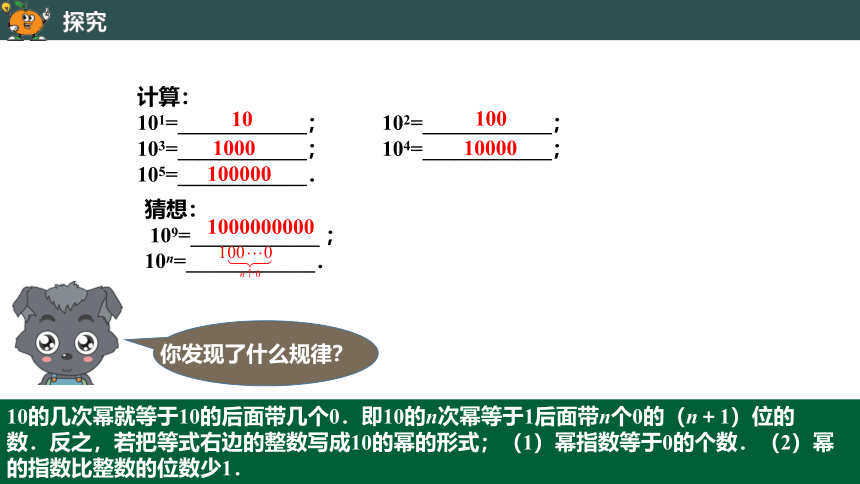
计算:
101=____________; 102=____________;
103=____________; 104=____________;
105=____________.
猜想:
109=____________ ;
10n=____________.
你发现了什么规律?
10的几次幂就等于10的后面带几个0.即10的n次幂等于1后面带n个0的(n+1)位的数.反之,若把等式右边的整数写成10的幂的形式;(1)幂指数等于0的个数.(2)幂的指数比整数的位数少1.
10
100
1000
10000
100000
1000000000
探究
你能借用10的乘方的方法来表示较大的数吗?
600000=6×_____________=6×_____________;
100000
105
20000000=2×_____________=2×_____________;
10000000
107
6500000=6.5×_____________=6.5×___________;
1000000
106
科学记数法:把一个数表示成a(1≤a<10)与10的幂相乘的形式,叫做科学记数法.
探究
1、科学记数法中与10的幂相乘的数a,必须是整数数位只有一位的数,即1≤a<10.
2、10的幂指数n比原数整数数位少1.所以,用科学记数法表示的数,一个突出的特点就是这个数的整数数位一目了然,这对于判断一个数的大小是非常方便的.
总结
例3 (1)用科学记数法表示下列各数:
23 000; .
(2)下列用科学记数法表示的数,原来(指和一般10进制记数法表示的结果)各是什么数?
4.315×103; 1.02×106;
(3)计算:(8.1×108)÷(9×105).
解:(1)230 000=2.3×105;
.
(2)4.315×103=4315;
1.02×106=1020000.
(3)
.
例题讲解
1、用科学记数法表示下列各数:
314000; 510000000; .
解: 314000=3.14×105;
.
510000000=5.1×108;
2、下列用科学记数法表示的数,原来各是什么数?
7×107,2.3×103,6.05×106,-1.93×104.
解:7×107=30000000, 2.3×103=2300,
6.05×106=6050000, -1.93×104=-19300.
3、计算(6×1013)÷(1.2×104).
.
变式练习
例4 如果平均每人每天需要粮食0.5 kg,那么全国每天大约需要粮食多少kg?1年呢(全国人口约1.37×109人,结果用科学记数法表示)?
解:0.5×1.37×109
=0.685×1 000 000 000
=6850 000 000
=6.85×108(kg).
按一年为365天计算,
6.85×108×365
=6.85×365×100 000 000
=250 025 000 000
≈2.5×1011(kg).
答:全国一天大约需要粮食6.85×108kg,一年大约需要粮食2.5×1011kg.
例题讲解
1.PM2.5是指大气中直径小于或等于2.5×10﹣3毫米的颗粒物,也称为可入肺颗粒物,把2.5×10﹣3用小数形式表示正确的是( )A.0.000025 B.0.00025 C.0.0025 D.0.025
【分析】科学记数法的标准形式为a×10n(1≤|a|<10,n为整数),n是负几小数点向左移动几位就可以得到.21*cnjy*com
解:2.5×10﹣3用小数形式表示正确的是0.0025,
故选:C.
课后练习
2、用科学记数法表示下列各数:
(1)-800200;(2)2021;(3)1000;(4)-301.
解:(1)-800200=-8.002×105;
(2)2021=2.021×103;
(3)10000=1×104;
(4)-301=-3.01×102.
课后练习
3、将下列用科学记数法表示的数还原:
(1)2.21×103;
(2)6.0×108;
(3)5.03×105.
解:(1)2.21×103=2210,
(2)6.0×108=600000000,
(3)5.03×105=503000.
课后练习
4.已知一台计算机的运算速度为1.2×109次/秒.
(1)求这台计算机6×103秒运算了多少次?
(2)若该计算机完成一道证明题需要进行1.08×1013次运算,求完成这道证明题需要多少分钟?
解:(1)这台计算机6×103秒,则一共计算了:6×103×1.2×109=7.2×1012(次),
答:这台计算机6×103秒运算了7.2×1012次;
(2)由题意可得:1.08×1013÷1.2×109=9×103(秒)=150(分钟),
答:完成这道证明题需要150分钟.
课后练习
把一个数表示成a(1≤a<10)与10的幂相乘的形式,叫做科学记数法.
科学记数法中与10的幂相乘的数a,必须是整数数位只有一位的数,即1≤a<10. 10的幂指数n比原数整数数位少1.
课后小结
教材练习题
课后作业
谢
谢
观
看
1.有理数的乘方:求几个相同因数的积的运算叫做乘方.
2.幂的性质:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.0的任何正整数次幂都为0.
3 .有理数运算顺序:对于有理数的混合运算,应先算乘方,再算乘除,最后算加减,如果遇到括号,就先进行括号里的运算.
知识回顾
情境一:2003年10月15日,中国首次进行载人航天飞行,飞船绕地球飞行了14圈,行程约60万 km,已知赤道长度约40000 km,飞船行程相当于多少个赤道长?
情境二:如果某市每人每天节约用水0.5千克,该市约有1千3百万人口,那么该市每天节约用水多少千克?
在日常的生产和生活中,我们经常遇到一些较大的数,怎样使较大的数读写方便呢?
导入新课
计算:
101=____________; 102=____________;
103=____________; 104=____________;
105=____________.
猜想:
109=____________ ;
10n=____________.
你发现了什么规律?
10的几次幂就等于10的后面带几个0.即10的n次幂等于1后面带n个0的(n+1)位的数.反之,若把等式右边的整数写成10的幂的形式;(1)幂指数等于0的个数.(2)幂的指数比整数的位数少1.
10
100
1000
10000
100000
1000000000
探究
你能借用10的乘方的方法来表示较大的数吗?
600000=6×_____________=6×_____________;
100000
105
20000000=2×_____________=2×_____________;
10000000
107
6500000=6.5×_____________=6.5×___________;
1000000
106
科学记数法:把一个数表示成a(1≤a<10)与10的幂相乘的形式,叫做科学记数法.
探究
1、科学记数法中与10的幂相乘的数a,必须是整数数位只有一位的数,即1≤a<10.
2、10的幂指数n比原数整数数位少1.所以,用科学记数法表示的数,一个突出的特点就是这个数的整数数位一目了然,这对于判断一个数的大小是非常方便的.
总结
例3 (1)用科学记数法表示下列各数:
23 000; .
(2)下列用科学记数法表示的数,原来(指和一般10进制记数法表示的结果)各是什么数?
4.315×103; 1.02×106;
(3)计算:(8.1×108)÷(9×105).
解:(1)230 000=2.3×105;
.
(2)4.315×103=4315;
1.02×106=1020000.
(3)
.
例题讲解
1、用科学记数法表示下列各数:
314000; 510000000; .
解: 314000=3.14×105;
.
510000000=5.1×108;
2、下列用科学记数法表示的数,原来各是什么数?
7×107,2.3×103,6.05×106,-1.93×104.
解:7×107=30000000, 2.3×103=2300,
6.05×106=6050000, -1.93×104=-19300.
3、计算(6×1013)÷(1.2×104).
.
变式练习
例4 如果平均每人每天需要粮食0.5 kg,那么全国每天大约需要粮食多少kg?1年呢(全国人口约1.37×109人,结果用科学记数法表示)?
解:0.5×1.37×109
=0.685×1 000 000 000
=6850 000 000
=6.85×108(kg).
按一年为365天计算,
6.85×108×365
=6.85×365×100 000 000
=250 025 000 000
≈2.5×1011(kg).
答:全国一天大约需要粮食6.85×108kg,一年大约需要粮食2.5×1011kg.
例题讲解
1.PM2.5是指大气中直径小于或等于2.5×10﹣3毫米的颗粒物,也称为可入肺颗粒物,把2.5×10﹣3用小数形式表示正确的是( )A.0.000025 B.0.00025 C.0.0025 D.0.025
【分析】科学记数法的标准形式为a×10n(1≤|a|<10,n为整数),n是负几小数点向左移动几位就可以得到.21*cnjy*com
解:2.5×10﹣3用小数形式表示正确的是0.0025,
故选:C.
课后练习
2、用科学记数法表示下列各数:
(1)-800200;(2)2021;(3)1000;(4)-301.
解:(1)-800200=-8.002×105;
(2)2021=2.021×103;
(3)10000=1×104;
(4)-301=-3.01×102.
课后练习
3、将下列用科学记数法表示的数还原:
(1)2.21×103;
(2)6.0×108;
(3)5.03×105.
解:(1)2.21×103=2210,
(2)6.0×108=600000000,
(3)5.03×105=503000.
课后练习
4.已知一台计算机的运算速度为1.2×109次/秒.
(1)求这台计算机6×103秒运算了多少次?
(2)若该计算机完成一道证明题需要进行1.08×1013次运算,求完成这道证明题需要多少分钟?
解:(1)这台计算机6×103秒,则一共计算了:6×103×1.2×109=7.2×1012(次),
答:这台计算机6×103秒运算了7.2×1012次;
(2)由题意可得:1.08×1013÷1.2×109=9×103(秒)=150(分钟),
答:完成这道证明题需要150分钟.
课后练习
把一个数表示成a(1≤a<10)与10的幂相乘的形式,叫做科学记数法.
科学记数法中与10的幂相乘的数a,必须是整数数位只有一位的数,即1≤a<10. 10的幂指数n比原数整数数位少1.
课后小结
教材练习题
课后作业
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
