2.7近似数 教学课件(共23张PPT)
文档属性
| 名称 | 2.7近似数 教学课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览








文档简介
近似数
曾侯乙编钟是1978年春夏之交被发掘而问世,是战国时代初期南部诸候国曾国国君曾候乙的殡葬物。由64个青铜编钟组成,分3层排列,共8组,最大的高153.4厘米,最小的高20.2厘米,其造型壮观,配备齐全,音列充实,音顿准确,堪称中国古代编钟之最,经考古判断,该编钟是约2400年前春秋晚期的文物.
新课导入
上面节前语中,64这个数与曾侯乙编钟的实际个数完全符合.像这样与实际完全符合的数称为准确数.在节前语中,3, 8 这两个数也是准确数.153.4, 20.2, 2400这三个数是通过测量或估计得到的,它们与最大编钟和最小编钟的实际高度,以及制造编钟的实际年代比较接近,但不完全符合.像这样与实际接近的数称为近似数.
新课导入
什么叫准确数?
什么叫近似数?
与实际完全符合的数称为准确数。
与实际接近的数称为近似数。
注意:通过测量或估计得到的都是近似数
归纳
下列叙述中的各数,哪些是准确数?哪些是近似数?说明你的理由.
(1)教室里有24张课桌;
(2)小明的身高为1.57 m;
(3)某本书的定价是4.5元;
(4)月球与地球之间的平均距离大约是38万千米;
(5)美国一家猫粮制作公司称:在美国共有8500万只猫咪,22%的猫主人都选择猫咪爱看的频道.
近似数
近似数
近似数
准确数
准确数
做一做
下列问题中,哪些是近似数?哪些是精确数?
(1)餐桌的长度是2.13 米;
(2)一星期有 7天;
(3)光的速度是每秒 30万千米;?
(4)李刚家共有4 口人;
(5)七(6)班有50名学生;
(6)小华的体重是 43.1公斤.
近似数
近似数
准确数
近似数
准确数
准确数
练习
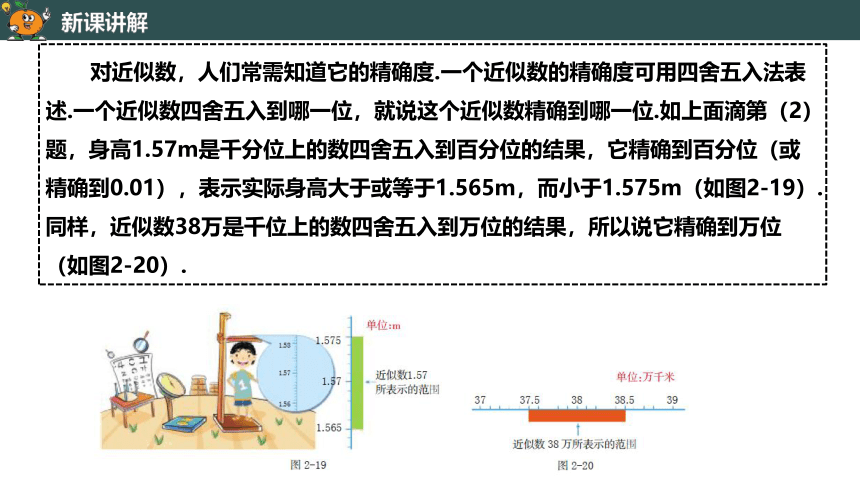
对近似数,人们常需知道它的精确度.一个近似数的精确度可用四舍五入法表述.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.如上面滴第(2)题,身高1.57m是千分位上的数四舍五入到百分位的结果,它精确到百分位(或精确到0.01),表示实际身高大于或等于1.565m,而小于1.575m(如图2-19).同样,近似数38万是千位上的数四舍五入到万位的结果,所以说它精确到万位(如图2-20).
新课讲解
下列由四舍五入法得到的近似数各精确到哪一位?
(1)11亿; (2)36.8; (3)1.2万; (4)1.20万.
解:(1)11亿精确到亿位,因为11亿=1100 000 000;
(2)36.8,精确到十分位;
(3)1.2万精确到千位,因为1.2万=12 000;
(4)1.20万精确到百位,因为1.20万=12 000.
两点注意:
1、两个近似数 1.2 与 1.20 表示的精确度不同.
2、两个近似数 1.2万 与 1.2 精确到的数位不同.
做一做
用四舍五入法,按括号内的要求对下列各数取近似值.
(1)0.33448(精确到千分位);
(2)64.8(精确到个位);
(3)1.5952(精确到0.01);
(4)0.05069(精确到0.001);
(5)85960(精确到百位,并用科学记数法表示).
解: (1) 0.33448≈0.334;
(2)64.8≈65;
(3)1.5046≈1.50;
(4)0.05069 ≈0.051;
(5)85960 ≈86000≈8.60×104.
做一做
一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
用四舍五入法时:
(1)明确需要确定到哪一位.
(2)根据需要把精确度后一位数字四舍五入.
归纳
近似数的计算我们一般用计算器作为辅助计算工具,人们常用的计算器有简易计算器、科学计算器(如图2-21)和图形计算器等.用科学计算器进行混合运算的按键顺序与书写顺序基本相同。近似计算中可按精确度要求求将用计算器算得的结果取近似值.
新课讲解
例1 用计算器计算:
(1) ;
(2) (精确到个位).
解:(1)按键顺序为:
显示:
∴
.
(2)按键顺序为:
显示:
∴
.
例题讲解
例2 杭州市2009年献血量从2008年的46170升增加到48755升,增长的百分比是多少(精确以0.01%)?
解:2009年比2008年增长的百分比为 .
用计算器计算,按键顺序为:
显示:
∴ .
答:杭州市献血量2009年比2008年增长5.60%.
例题讲解
1.近似数5.0×102精确到( )
A.十分位 B.个位 C.十位 D.百位
解:近似数5.0×102精确到十位.
故选C.
课后练习
2.对于用四舍五入法得到的近似数4.609万,下列说法中正确的是( )
A.它精确到千分位 B.它精确到0.01
C.它精确到万位 D.它精确到十位
解:4.609万精确到0.001万,即十位.
故选D.
课后练习
3.下列说法正确的是( )
A.近似数3.5和3.50精确度相同
B.近似数0.0120有3个有效数字
C.近似数7.05×104精确到百分位
D.近似数3千和3000的有效数字都是3
解:A、近似数3.5精确到十分位,3.50精确到百分位,故A错误;
B、近似数0.0120有3个有效数字,故B正确;
C、近似数7.05×104精确到百位,故C错误;
D、近似数3千的有效数字是3,而3000的有效数字都是3,0,0,0,故D错误;
故选B.
课后练习
4、下列由四舍五入法得到的近似数,各精确到哪一位?
(1)136.32;(2)0.0301;(3)19.053;
(4)320.03;(5)4.001.
解:(1)136.32精确到百分位;(2)0.0301精确到万分位;
(3)19.053精确到千分位;(4)320.03精确到百位;
(5)4.001精确到千分位.
课后练习
5、用计算器求下列各式的值:
(1)24.12×2+3.452×4.2;(精确到0.1);???
(2)(2.42-1.32)×3.1+4.13;(精确到0.01).
解:(1)24.12×2+3.452×4.2,
=1211.6105,
≈1211.6;
(2)(2.42-1.32)×3.1+4.13,
=81.538,
≈81.54.
课后练习
6.小丽与小明在讨论问题:
小丽:如果你把7498近似到4位数,你就会得到7000.
小明:不,我有另外一种解答方法,可以得到不同的答案,首先,将7498近似到百位,得到7500,接着再把7500近似到千位,就得到8000.
你怎样评价小丽和小明的说法呢?
解:小丽是正确的,小明错误.
7498近似到4位数,要把百位上的数字四舍五入即可.
课后练习
7.一名宇航员向地球总站发回两组数据:甲、乙两颗行星的直径分别为6.1×104千米和6.10×104千米,这两组数据之间有差别吗?如果没有,请说明理由;如果有,请说明有哪些差别.
解:有差别.
因为6.1×104精确到千位,有2个有效数字,
而6.10×104精确到百位,有3个有效数字.
课后练习
1、准确数和近似数.
2、精确度即表示一个近似数近似的程度.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
3、计算器
分类:简单计算器、科学技术器、图形计算器.
构造:键盘、面板.
课后总结
课后练习题
课后作业
谢
谢
观
看
曾侯乙编钟是1978年春夏之交被发掘而问世,是战国时代初期南部诸候国曾国国君曾候乙的殡葬物。由64个青铜编钟组成,分3层排列,共8组,最大的高153.4厘米,最小的高20.2厘米,其造型壮观,配备齐全,音列充实,音顿准确,堪称中国古代编钟之最,经考古判断,该编钟是约2400年前春秋晚期的文物.
新课导入
上面节前语中,64这个数与曾侯乙编钟的实际个数完全符合.像这样与实际完全符合的数称为准确数.在节前语中,3, 8 这两个数也是准确数.153.4, 20.2, 2400这三个数是通过测量或估计得到的,它们与最大编钟和最小编钟的实际高度,以及制造编钟的实际年代比较接近,但不完全符合.像这样与实际接近的数称为近似数.
新课导入
什么叫准确数?
什么叫近似数?
与实际完全符合的数称为准确数。
与实际接近的数称为近似数。
注意:通过测量或估计得到的都是近似数
归纳
下列叙述中的各数,哪些是准确数?哪些是近似数?说明你的理由.
(1)教室里有24张课桌;
(2)小明的身高为1.57 m;
(3)某本书的定价是4.5元;
(4)月球与地球之间的平均距离大约是38万千米;
(5)美国一家猫粮制作公司称:在美国共有8500万只猫咪,22%的猫主人都选择猫咪爱看的频道.
近似数
近似数
近似数
准确数
准确数
做一做
下列问题中,哪些是近似数?哪些是精确数?
(1)餐桌的长度是2.13 米;
(2)一星期有 7天;
(3)光的速度是每秒 30万千米;?
(4)李刚家共有4 口人;
(5)七(6)班有50名学生;
(6)小华的体重是 43.1公斤.
近似数
近似数
准确数
近似数
准确数
准确数
练习
对近似数,人们常需知道它的精确度.一个近似数的精确度可用四舍五入法表述.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.如上面滴第(2)题,身高1.57m是千分位上的数四舍五入到百分位的结果,它精确到百分位(或精确到0.01),表示实际身高大于或等于1.565m,而小于1.575m(如图2-19).同样,近似数38万是千位上的数四舍五入到万位的结果,所以说它精确到万位(如图2-20).
新课讲解
下列由四舍五入法得到的近似数各精确到哪一位?
(1)11亿; (2)36.8; (3)1.2万; (4)1.20万.
解:(1)11亿精确到亿位,因为11亿=1100 000 000;
(2)36.8,精确到十分位;
(3)1.2万精确到千位,因为1.2万=12 000;
(4)1.20万精确到百位,因为1.20万=12 000.
两点注意:
1、两个近似数 1.2 与 1.20 表示的精确度不同.
2、两个近似数 1.2万 与 1.2 精确到的数位不同.
做一做
用四舍五入法,按括号内的要求对下列各数取近似值.
(1)0.33448(精确到千分位);
(2)64.8(精确到个位);
(3)1.5952(精确到0.01);
(4)0.05069(精确到0.001);
(5)85960(精确到百位,并用科学记数法表示).
解: (1) 0.33448≈0.334;
(2)64.8≈65;
(3)1.5046≈1.50;
(4)0.05069 ≈0.051;
(5)85960 ≈86000≈8.60×104.
做一做
一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
用四舍五入法时:
(1)明确需要确定到哪一位.
(2)根据需要把精确度后一位数字四舍五入.
归纳
近似数的计算我们一般用计算器作为辅助计算工具,人们常用的计算器有简易计算器、科学计算器(如图2-21)和图形计算器等.用科学计算器进行混合运算的按键顺序与书写顺序基本相同。近似计算中可按精确度要求求将用计算器算得的结果取近似值.
新课讲解
例1 用计算器计算:
(1) ;
(2) (精确到个位).
解:(1)按键顺序为:
显示:
∴
.
(2)按键顺序为:
显示:
∴
.
例题讲解
例2 杭州市2009年献血量从2008年的46170升增加到48755升,增长的百分比是多少(精确以0.01%)?
解:2009年比2008年增长的百分比为 .
用计算器计算,按键顺序为:
显示:
∴ .
答:杭州市献血量2009年比2008年增长5.60%.
例题讲解
1.近似数5.0×102精确到( )
A.十分位 B.个位 C.十位 D.百位
解:近似数5.0×102精确到十位.
故选C.
课后练习
2.对于用四舍五入法得到的近似数4.609万,下列说法中正确的是( )
A.它精确到千分位 B.它精确到0.01
C.它精确到万位 D.它精确到十位
解:4.609万精确到0.001万,即十位.
故选D.
课后练习
3.下列说法正确的是( )
A.近似数3.5和3.50精确度相同
B.近似数0.0120有3个有效数字
C.近似数7.05×104精确到百分位
D.近似数3千和3000的有效数字都是3
解:A、近似数3.5精确到十分位,3.50精确到百分位,故A错误;
B、近似数0.0120有3个有效数字,故B正确;
C、近似数7.05×104精确到百位,故C错误;
D、近似数3千的有效数字是3,而3000的有效数字都是3,0,0,0,故D错误;
故选B.
课后练习
4、下列由四舍五入法得到的近似数,各精确到哪一位?
(1)136.32;(2)0.0301;(3)19.053;
(4)320.03;(5)4.001.
解:(1)136.32精确到百分位;(2)0.0301精确到万分位;
(3)19.053精确到千分位;(4)320.03精确到百位;
(5)4.001精确到千分位.
课后练习
5、用计算器求下列各式的值:
(1)24.12×2+3.452×4.2;(精确到0.1);???
(2)(2.42-1.32)×3.1+4.13;(精确到0.01).
解:(1)24.12×2+3.452×4.2,
=1211.6105,
≈1211.6;
(2)(2.42-1.32)×3.1+4.13,
=81.538,
≈81.54.
课后练习
6.小丽与小明在讨论问题:
小丽:如果你把7498近似到4位数,你就会得到7000.
小明:不,我有另外一种解答方法,可以得到不同的答案,首先,将7498近似到百位,得到7500,接着再把7500近似到千位,就得到8000.
你怎样评价小丽和小明的说法呢?
解:小丽是正确的,小明错误.
7498近似到4位数,要把百位上的数字四舍五入即可.
课后练习
7.一名宇航员向地球总站发回两组数据:甲、乙两颗行星的直径分别为6.1×104千米和6.10×104千米,这两组数据之间有差别吗?如果没有,请说明理由;如果有,请说明有哪些差别.
解:有差别.
因为6.1×104精确到千位,有2个有效数字,
而6.10×104精确到百位,有3个有效数字.
课后练习
1、准确数和近似数.
2、精确度即表示一个近似数近似的程度.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
3、计算器
分类:简单计算器、科学技术器、图形计算器.
构造:键盘、面板.
课后总结
课后练习题
课后作业
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
