浙教版 2.3有理数的乘法 第1课时 同步课件(22张PPT)
文档属性
| 名称 | 浙教版 2.3有理数的乘法 第1课时 同步课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览







文档简介
有理数的乘法一
图中显示的是位于三峡白鹤梁的用做水位测量标志的线刻石鱼.假设水位按每小时3厘米的速度下降,经2小时后水位下降多少厘米?
新课导入
由小学里学过的乘法的意义,可列出怎样算式?
如何在数轴上表示?
3×2=3+3=6.
若以某一时刻的水位为基准,规定水位上升为正,下降为负,你会列出怎样的算式?
(-3)×2.
所以(-3)×2=-6
新课讲解
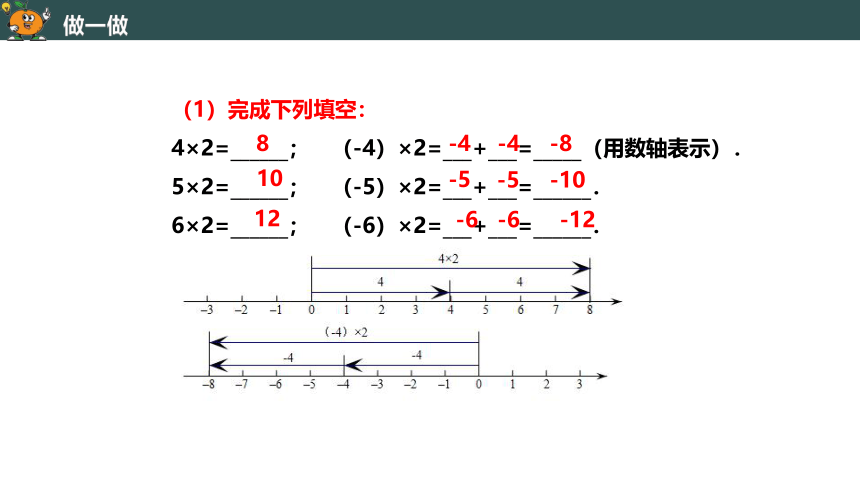
(1)完成下列填空:
4×2=______; (-4)×2=___+___=_____(用数轴表示).
5×2=______; (-5)×2=___+___=______.
6×2=______; (-6)×2=___+___=______.
8
-4
-4
-8
10
-5
-5
-10
12
-6
-6
-12
做一做
(2)观察上面左右两列算式中相乘两数及计算结果的符号,你有什么发现?
(+4)×(+2)= +8
(-4)× (+2) = -8
当改变相乘两数中一个数的符号时,其积就变为原来积的相反数.
做一做
根据你的发现写出下列各算式的结果:
3×7=________, (-3)×7=________,
3×(-7)=_________, (-3)×(-7)=_______,
0 ×7=_______, 0×(-7)=______.
(1)两数相乘时,积的符号与这两个数的符号有什么关系?
(2)积的绝对值与这两个乘数的绝对值有什么关系?
有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘,都得0.
21
21
-21
-21
0
0
做一做
不计算,直接确定下列积的符号:
(1) 30×(-10)
(2) (-1)×2
(3) (-3)×(-9)
(4) 1.1×2.7
-
+
-
+
针对训练
例1 计算:
(1) ; (2)(-2.5)×4; (3)(-5)×0 × ;
(4) ; (5) .
解:(1)
(2)(-2.5)×4=-(2.5 ×4 )=1
(3)
(4)
(5)
例题讲解
有理数乘法运算步骤:
再确定积的符号
后进行绝对值的乘法运算
先判断类型
(同号、异号等)
归纳
几个有理数相乘怎样确定积的符号呢?
观察下列各式,它们的积是正的还是负的?并计算进行验证.
(1)(-1) ×2 ×3 ×4
(2) (-1) ×(-2 )×3 ×4
(3) (-1) ×(-2 )×(-3 )×4
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
=-24
=+24
=-24
=+24
=0
多个不为零的有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数时,则积为正;
负因数的个数为奇数时,则积为负;
几个有理数相乘,当有一个因数为 0 时,积为0 .
归纳
与 的乘积等于1, 与-3的乘积等于1.
若两个有理数乘积为1,
就称这两个有理数互为倒数.
0有倒数吗?为什么?
注意:0没有倒数.
如 的倒数是 , 的倒数是 .
注意
(1)0没有倒数.
(2)求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
(3)正数的倒数是正数,负数的倒数是负数.
(4)求小数的倒数时,要先把小数化成分数.
(5)求带分数的倒数时,要先把带分数化成假分数.
归纳
1.计算(﹣3)×|﹣2|的结果等于( )
A.6 B.5 C.﹣6 D.﹣5
解:原式=(﹣3)×2
=﹣6.
故选C.
课后练习
2.若a+b<0,ab<0,则( )
A.a>0,b>0
B.a<0,b<0
C.a,b两数一正一负,且正数的绝对值大于负数的绝对值
D.a,b两数一正一负,且负数的绝对值大于正数的绝对值
解:∵ab<0,
∴a、b异号,
又∵a+b<0,
∴负数的绝对值大于正数的绝对值.
故选D.
课后练习
(1)2×3×4×(-5)
(2)2×3×(-4) ×(-5)
(3) 2×(-3) ×(-4) ×(-5)
(4) (-2) ×(-3) ×(-4) ×(-5)
=-120
=+120
=-120
=+120
3.计算
课后练习
4.求下列各数的倒数:
(1) - 2 (2)- 1 (3 )1
(4) (5) 1.2
解:(1)-3的倒数是 ;(2)-1的倒数是-1;
(3)1的倒数是1; (4) 的倒数是 ;
(5) 1.2的倒数是 ;
课后练习
5.计算:
(1)(-25)×(+4.8); (2) ;
(3)0 ×(-9.5); (4) .
解:(1)(-25)×(+4.8)=-(25 × 4.8)=-120;
(2) ;
(3)0 ×(-9.5)=0;
(4) .
课后练习
6.如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
课后练习
【分析】(1)将点A向右移动3个单位长度得到点C的位置,依据相反数的定义得到点B表示的数;
(2)依据有理数的乘法法则计算即可;
(3)找出AB的中点,然后可得到与点C重合的数.
解:(1)如图所示:
(2)﹣5×2=﹣10.
(3)A、B中点所表示的数为﹣3,点C与数﹣8所表示的点重合.
故答案为:﹣8.
课后练习
1、有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0.
2、多个不为零的有理数相乘,积的符号由负因数的个数确定:负因数的个数为偶数时,则积为正;负因数的个数为奇数时,则积为负;几个有理数相乘,当有一个因数为 0 时,积为0 .
3、若两个有理数乘积为1,就称这两个有理数互为倒数.
课堂小结
教材练习题
课后作业
谢
谢
观
看
图中显示的是位于三峡白鹤梁的用做水位测量标志的线刻石鱼.假设水位按每小时3厘米的速度下降,经2小时后水位下降多少厘米?
新课导入
由小学里学过的乘法的意义,可列出怎样算式?
如何在数轴上表示?
3×2=3+3=6.
若以某一时刻的水位为基准,规定水位上升为正,下降为负,你会列出怎样的算式?
(-3)×2.
所以(-3)×2=-6
新课讲解
(1)完成下列填空:
4×2=______; (-4)×2=___+___=_____(用数轴表示).
5×2=______; (-5)×2=___+___=______.
6×2=______; (-6)×2=___+___=______.
8
-4
-4
-8
10
-5
-5
-10
12
-6
-6
-12
做一做
(2)观察上面左右两列算式中相乘两数及计算结果的符号,你有什么发现?
(+4)×(+2)= +8
(-4)× (+2) = -8
当改变相乘两数中一个数的符号时,其积就变为原来积的相反数.
做一做
根据你的发现写出下列各算式的结果:
3×7=________, (-3)×7=________,
3×(-7)=_________, (-3)×(-7)=_______,
0 ×7=_______, 0×(-7)=______.
(1)两数相乘时,积的符号与这两个数的符号有什么关系?
(2)积的绝对值与这两个乘数的绝对值有什么关系?
有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘,都得0.
21
21
-21
-21
0
0
做一做
不计算,直接确定下列积的符号:
(1) 30×(-10)
(2) (-1)×2
(3) (-3)×(-9)
(4) 1.1×2.7
-
+
-
+
针对训练
例1 计算:
(1) ; (2)(-2.5)×4; (3)(-5)×0 × ;
(4) ; (5) .
解:(1)
(2)(-2.5)×4=-(2.5 ×4 )=1
(3)
(4)
(5)
例题讲解
有理数乘法运算步骤:
再确定积的符号
后进行绝对值的乘法运算
先判断类型
(同号、异号等)
归纳
几个有理数相乘怎样确定积的符号呢?
观察下列各式,它们的积是正的还是负的?并计算进行验证.
(1)(-1) ×2 ×3 ×4
(2) (-1) ×(-2 )×3 ×4
(3) (-1) ×(-2 )×(-3 )×4
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
=-24
=+24
=-24
=+24
=0
多个不为零的有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数时,则积为正;
负因数的个数为奇数时,则积为负;
几个有理数相乘,当有一个因数为 0 时,积为0 .
归纳
与 的乘积等于1, 与-3的乘积等于1.
若两个有理数乘积为1,
就称这两个有理数互为倒数.
0有倒数吗?为什么?
注意:0没有倒数.
如 的倒数是 , 的倒数是 .
注意
(1)0没有倒数.
(2)求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
(3)正数的倒数是正数,负数的倒数是负数.
(4)求小数的倒数时,要先把小数化成分数.
(5)求带分数的倒数时,要先把带分数化成假分数.
归纳
1.计算(﹣3)×|﹣2|的结果等于( )
A.6 B.5 C.﹣6 D.﹣5
解:原式=(﹣3)×2
=﹣6.
故选C.
课后练习
2.若a+b<0,ab<0,则( )
A.a>0,b>0
B.a<0,b<0
C.a,b两数一正一负,且正数的绝对值大于负数的绝对值
D.a,b两数一正一负,且负数的绝对值大于正数的绝对值
解:∵ab<0,
∴a、b异号,
又∵a+b<0,
∴负数的绝对值大于正数的绝对值.
故选D.
课后练习
(1)2×3×4×(-5)
(2)2×3×(-4) ×(-5)
(3) 2×(-3) ×(-4) ×(-5)
(4) (-2) ×(-3) ×(-4) ×(-5)
=-120
=+120
=-120
=+120
3.计算
课后练习
4.求下列各数的倒数:
(1) - 2 (2)- 1 (3 )1
(4) (5) 1.2
解:(1)-3的倒数是 ;(2)-1的倒数是-1;
(3)1的倒数是1; (4) 的倒数是 ;
(5) 1.2的倒数是 ;
课后练习
5.计算:
(1)(-25)×(+4.8); (2) ;
(3)0 ×(-9.5); (4) .
解:(1)(-25)×(+4.8)=-(25 × 4.8)=-120;
(2) ;
(3)0 ×(-9.5)=0;
(4) .
课后练习
6.如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
课后练习
【分析】(1)将点A向右移动3个单位长度得到点C的位置,依据相反数的定义得到点B表示的数;
(2)依据有理数的乘法法则计算即可;
(3)找出AB的中点,然后可得到与点C重合的数.
解:(1)如图所示:
(2)﹣5×2=﹣10.
(3)A、B中点所表示的数为﹣3,点C与数﹣8所表示的点重合.
故答案为:﹣8.
课后练习
1、有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0.
2、多个不为零的有理数相乘,积的符号由负因数的个数确定:负因数的个数为偶数时,则积为正;负因数的个数为奇数时,则积为负;几个有理数相乘,当有一个因数为 0 时,积为0 .
3、若两个有理数乘积为1,就称这两个有理数互为倒数.
课堂小结
教材练习题
课后作业
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
