6.2菱形(1)

(共16张PPT)
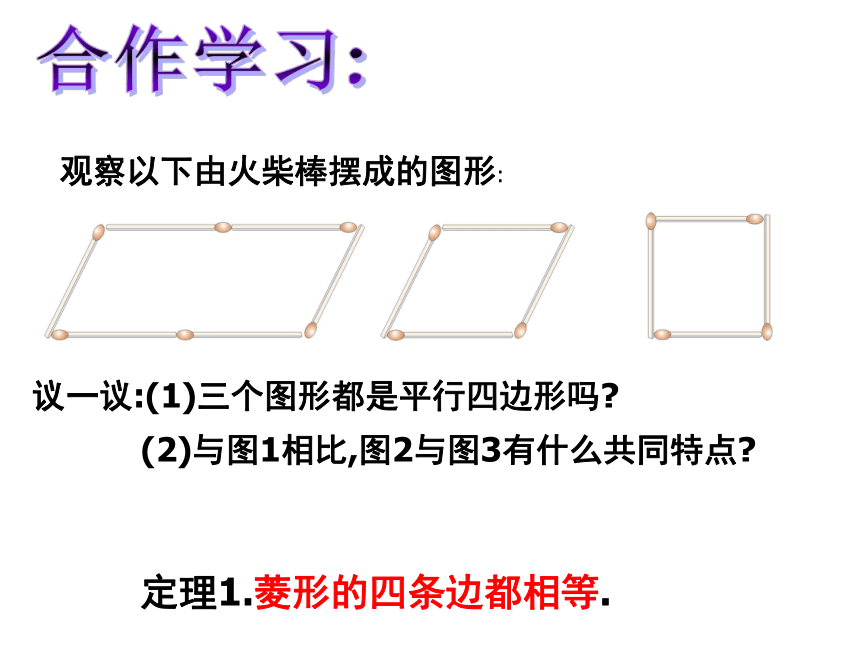
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗
(2)与图1相比,图2与图3有什么共同特点
定理1.菱形的四条边都相等.
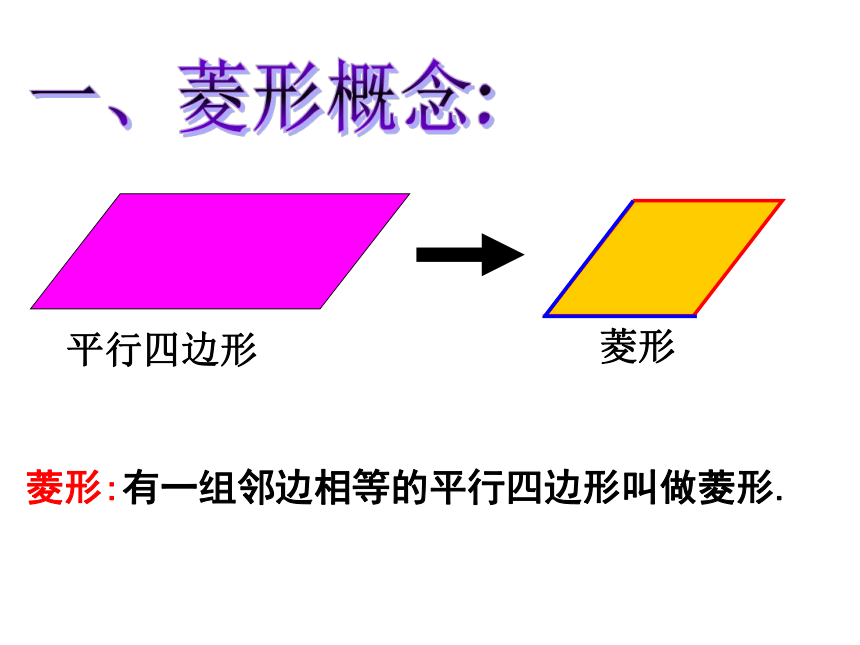
平行四边形
菱形
菱形:有一组邻边相等的平行四边形叫做菱形.
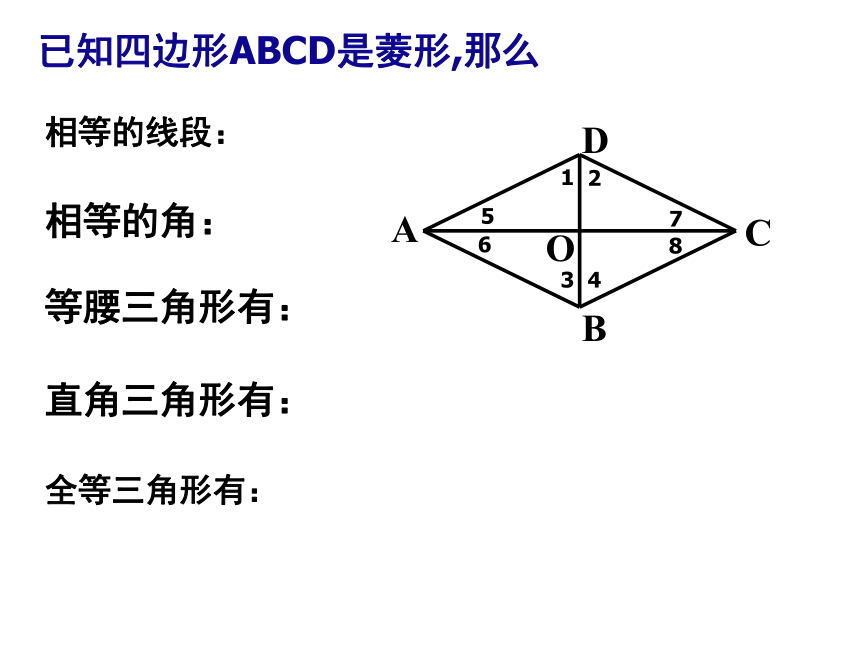
相等的线段：
相等的角：
等腰三角形有：
直角三角形有：
全等三角形有：
已知四边形ABCD是菱形,那么
1
2
3
4
5
6
7
8
A
B
C
D
O
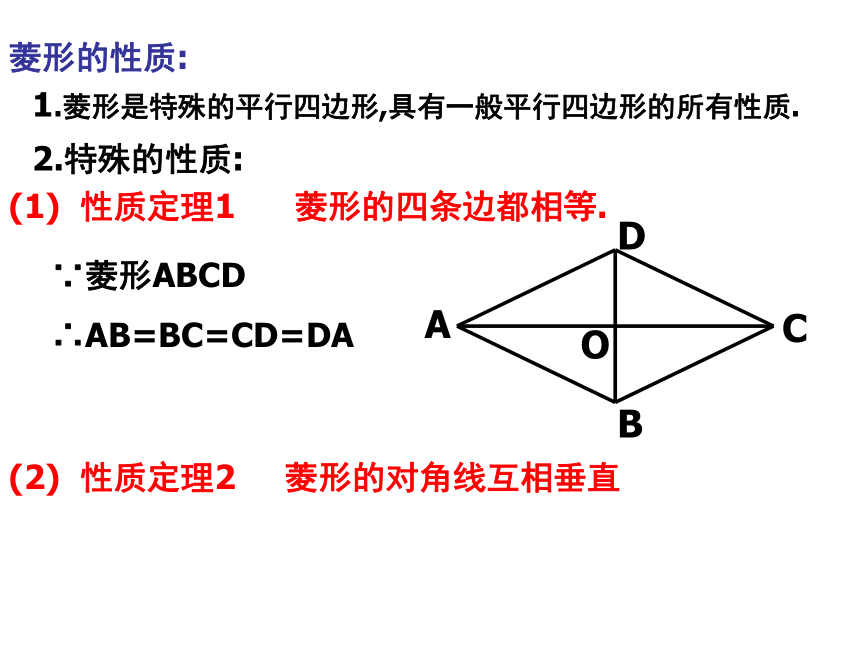
菱形的性质:
1.菱形是特殊的平行四边形,具有一般平行四边形的所有性质.
2.特殊的性质:
(1) 性质定理1 菱形的四条边都相等.
(2) 性质定理2 菱形的对角线互相垂直
∵菱形ABCD
∴AB=BC=CD=DA
A
B
C
D
O
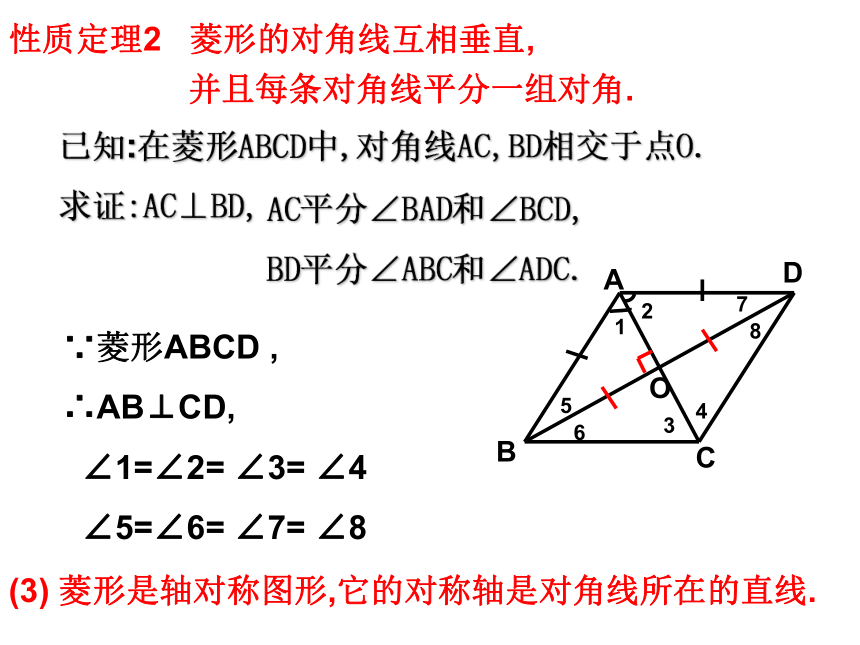
性质定理2 菱形的对角线互相垂直,
已知:在菱形ABCD中,对角线AC,BD相交于点O.
求证:AC⊥BD,
∵菱形ABCD ,
∴AB⊥CD,
∠1=∠2= ∠3= ∠4
∠5=∠6= ∠7= ∠8
3
4
5
6
7
8
O
B
C
A
D
(3) 菱形是轴对称图形,它的对称轴是对角线所在的直线.
并且每条对角线平分一组对角.
AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
1
2
.
.
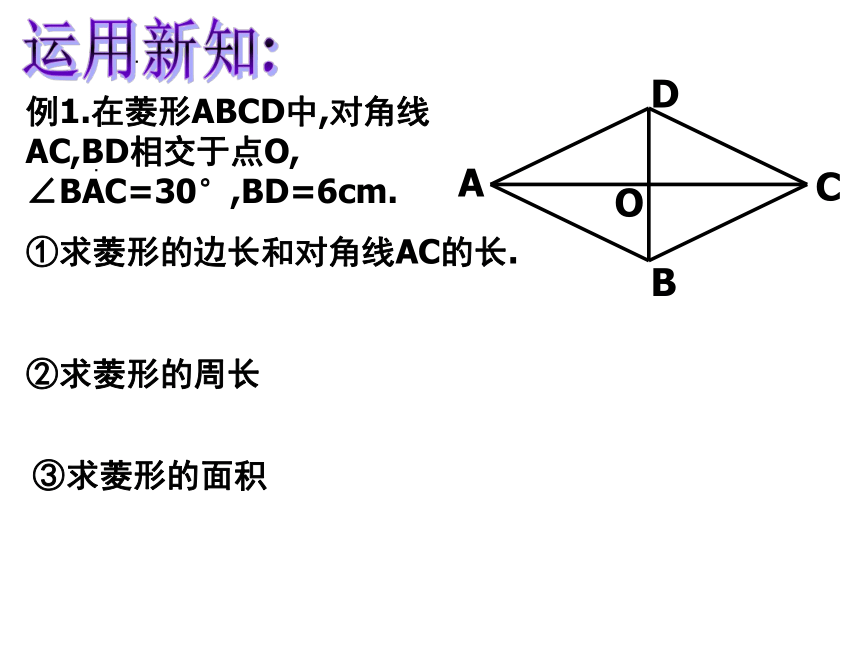
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6cm.
①求菱形的边长和对角线AC的长.
A
B
C
D
O
②求菱形的周长
③求菱形的面积
.
.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6cm.
A
B
C
D
O
④有两动点P，Q ，P：从A到B，
Q：从C到B，速度都是1cm/s，两点同时出发，找出运动过程始终全等的三角形，说明理由。
⑤当P，Q分别运动到AB，AC的中点时，问此时
DP与AB有什么位置关系
PQ的长时多少
(3)△DPQ是什么三角形
.
.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6cm.
A
B
C
D
O
④有两动点P，Q ，P：从A到B，
Q：从C到B，速度都是1cm/s，两点同时出发，找出运动过程始终全等的三角形，说明理由。
⑥若把第④小题中的Q，改为从B点出发，向C点运动，
在运动的过程中，有没有全等三角形
(2)在运动的过程中，∠PDQ为多少度
(3) 在运动的过程中△DPQ是什么三角形
2菱形的两条对角线长分别为6cm和8cm，则菱形的边长是（ ）
A.10cm B.7cm
C. 5cm D.4cm
3
4
C
菱形ABCD的面积是多少？
高是多少？
A
B
C
D
O
【菱形的面积公式】
A
B
C
D
O
面积：S菱形=底×高
=对角线乘积的一半
D
O
A
C
B
菱形ABCD的周长为16，邻角的度数比为1：2
1.求菱形ABCD的对角线的长；
2.求菱形ABCD的面积．
一路下来，大家收获不小吧！说说你的感受，让大家一起来分享，怎么样？
菱形所具有的特性：
1、菱形的四条边都相等
2、菱形的对角线互相垂直，且一条对角线平分一组对角
3、菱形的面积等于对角线乘积的一半
2、已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AB=1。
求（1）∠ABC的度数；
（2）对角线AC、BD的长；
（3）菱形ABCD的面积。
A
B
C
D
E
O
挑战自我
已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系
N
F
E
D
A
C
B
M
1
2
3
4