4.3 相似三角形性质及应用

(共15张PPT)
边长放大10倍
周长放大10倍
角度不变
面积放大100倍
观察—思考
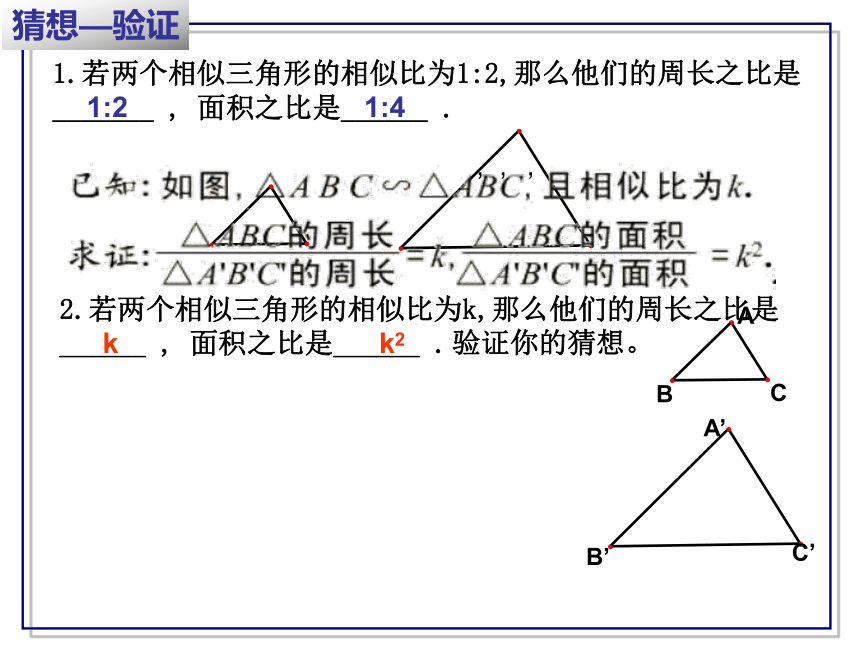
1.若两个相似三角形的相似比为1:2,那么他们的周长之比是_______ , 面积之比是______ .
猜想—验证
2.若两个相似三角形的相似比为k,那么他们的周长之比是______ , 面积之比是______ .
1:2
1:4
k
k2
验证你的猜想。
A
B
C
A’
B’
C’
’
’
’
相似三角形的性质
若两个相似三角形的相似比为k，则
(1).对应边上的高线，中线，对应角的角平分线之比为k.
(2).两个三角形的周长之比为k.
(3).两个三角形的面积之比为k2.
知识概括
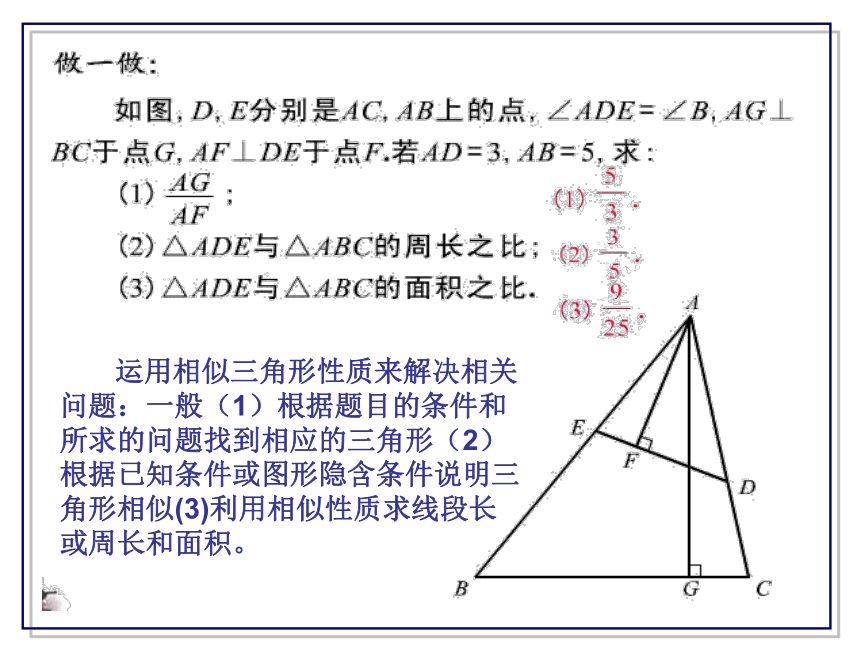
2.如图,DE∥BC，AD:BD=1:3，如果△ADE的周长等于5cm，那么△ABC的周长等于_____cm。S△ADE : S四边形DBCE=________
知识应用
运用相似三角形性质来解决相关问题：一般（1）根据题目的条件和所求的问题找到相应的三角形（2）根据已知条件或图形隐含条件说明三角形相似(3)利用相似性质求线段长或周长和面积。
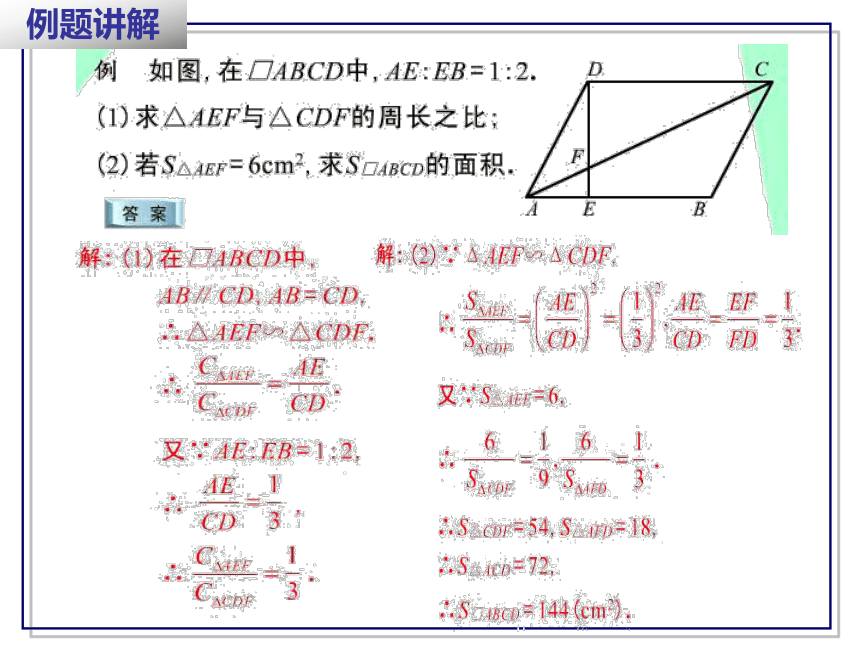
例题讲解
，
一
根据图形你能说说这个小组的测量方案吗？
C
A
B
B’
A’
C’
如图，把△ABC沿BC边平移到△A’B’C’的位置，使得他们重叠部分（图中阴影部分）的面积是△ABC面积的一半 , 若BC= ，则此三角形移动的距离BB’是多少？
如图，AD∥BC，∠D=90°，DC=7，AD=2，BC=3，点P在线段DC上，问：当PC的长为何值时，△PAD与△PBC相似？