浙教版七年级数学上册2.1有理数的加法同步练习附答案
文档属性
| 名称 | 浙教版七年级数学上册2.1有理数的加法同步练习附答案 | 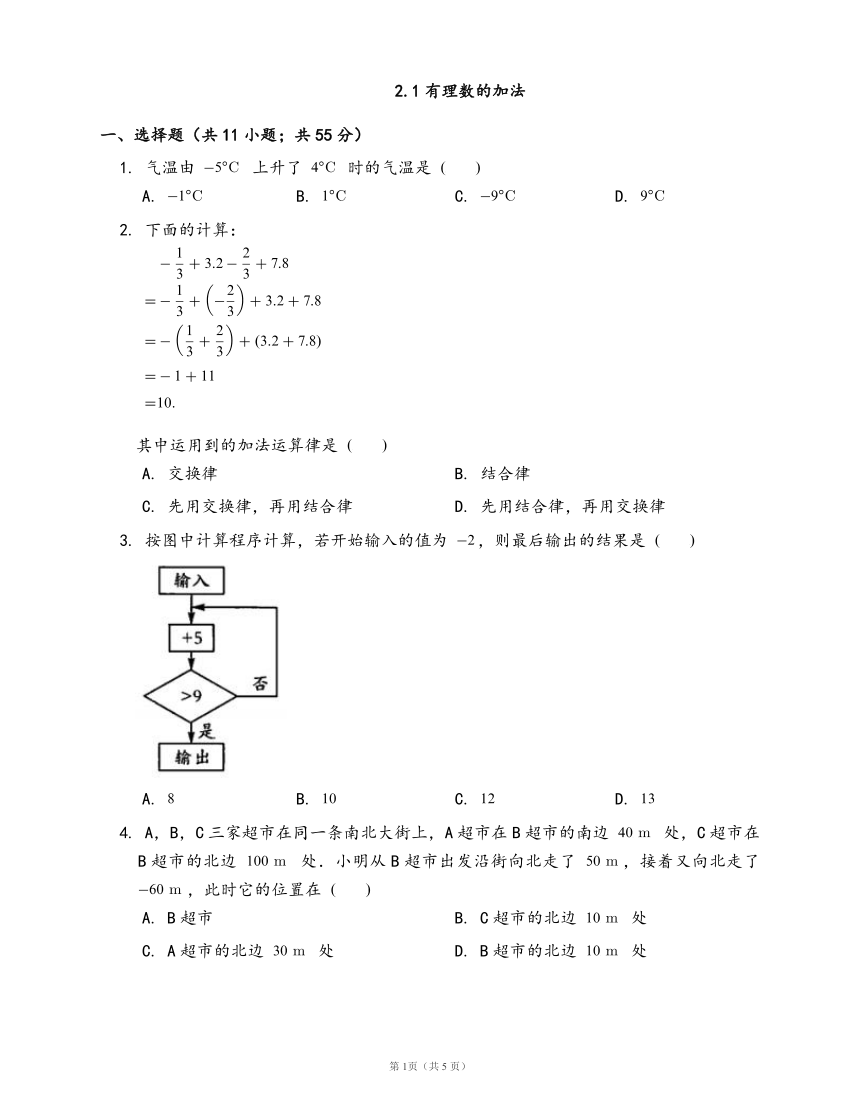 | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 17:18:00 | ||
图片预览


文档简介
2.1有理数的加法
一、选择题(共11小题;共55分)
1.
气温由
上升了
时的气温是
A.
B.
C.
D.
2.
下面的计算:
其中运用到的加法运算律是
A.
交换律
B.
结合律
C.
先用交换律,再用结合律
D.
先用结合律,再用交换律
3.
按图中计算程序计算,若开始输入的值为
,则最后输出的结果是
A.
B.
C.
D.
4.
A,B,C三家超市在同一条南北大街上,A超市在B超市的南边
处,C超市在B超市的北边
处.小明从B超市出发沿街向北走了
,接着又向北走了
,此时它的位置在
A.
B超市
B.
C超市的北边
处
C.
A超市的北边
处
D.
B超市的北边
处
5.
如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前
个格子中所填整数之和是
,则
的值可以是
A.
B.
C.
D.
6.
下列交换加数位置的变形中,正确的是
A.
B.
C.
D.
7.
王老师外出学习,
天后回到家里,他撕下了这
天的日历,发现这
天日期的数字相加的和为
,那么王老师回家这天是
A.
号
B.
号
C.
号
D.
号
8.
计算
的结果是
A.
B.
C.
D.
9.
下列各式中正确利用了加法运算律的是
A.
B.
C.
D.
10.
某公交车原坐有
人,经过
个站点时上、下车的人数情况如下(上车为正,下车为负):,,,,则车上还有
A.
人
B.
人
C.
人
D.
人
11.
把
这
个数填入
方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛書”(图
),是世界上最早的“幻方”.图
是仅可以看到部分数值的“九宫格”,则其中
的值为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
12.
,运用的有理数加法的
?律,如果
,,
是有理数,用
,,
的式子表示为
?.
13.
如果一辆汽车从仓库出发向东行驶了
千米后到达商场,卸完货向西行驶了
千米到达加油站,那么加油站位于仓库的
?面(填方向),距仓库
?千米.
14.
填空:
()
?;
()
?;
()
?;
()
?.
15.
某计算程序是:当输入一个数时,显示的结果总等于这个数的绝对值与
的和.若输入
,则显示的结果是
?;若输入某数后,显示的结果是
,则输入的数是
?.
16.
年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循一定的规律,如表所示:
那么第
颗行星到太阳的距离是
?天文单位.
三、解答题(共3小题;共40分)
17.
数学课上李老师提出一个问题:“绝对值小于
的整数共有多少个?”王明一下子举手了,老师请他回答,王明答道:“不就是
,,,,,,,,
这九个吗.”张华认为王明的回答有错,起来补充道:“李老师,王明还漏了
,,,,,,,,,所以一共有
个.”你觉得张华的补充完整了吗?为什么?
18.
将
,,,,,,,,
这
个数分别填入如图方阵的
个空格中,使得横,竖,斜对角的
个数相加的和相等.
19.
计算:.
答案
第一部分
1.
A
【解析】根据题意,得
,
则气温由
上升了
时的气温是
.
2.
C
3.
D
4.
C
5.
B
6.
D
7.
D
8.
B
9.
A
10.
B
11.
A
第二部分
12.
结合,
13.
西,
14.
,,,
15.
,
16.
第三部分
17.
不完整,还有零,共有
个.
18.
答案不唯一,如下:
19.
第2页(共5
页)
一、选择题(共11小题;共55分)
1.
气温由
上升了
时的气温是
A.
B.
C.
D.
2.
下面的计算:
其中运用到的加法运算律是
A.
交换律
B.
结合律
C.
先用交换律,再用结合律
D.
先用结合律,再用交换律
3.
按图中计算程序计算,若开始输入的值为
,则最后输出的结果是
A.
B.
C.
D.
4.
A,B,C三家超市在同一条南北大街上,A超市在B超市的南边
处,C超市在B超市的北边
处.小明从B超市出发沿街向北走了
,接着又向北走了
,此时它的位置在
A.
B超市
B.
C超市的北边
处
C.
A超市的北边
处
D.
B超市的北边
处
5.
如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前
个格子中所填整数之和是
,则
的值可以是
A.
B.
C.
D.
6.
下列交换加数位置的变形中,正确的是
A.
B.
C.
D.
7.
王老师外出学习,
天后回到家里,他撕下了这
天的日历,发现这
天日期的数字相加的和为
,那么王老师回家这天是
A.
号
B.
号
C.
号
D.
号
8.
计算
的结果是
A.
B.
C.
D.
9.
下列各式中正确利用了加法运算律的是
A.
B.
C.
D.
10.
某公交车原坐有
人,经过
个站点时上、下车的人数情况如下(上车为正,下车为负):,,,,则车上还有
A.
人
B.
人
C.
人
D.
人
11.
把
这
个数填入
方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛書”(图
),是世界上最早的“幻方”.图
是仅可以看到部分数值的“九宫格”,则其中
的值为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
12.
,运用的有理数加法的
?律,如果
,,
是有理数,用
,,
的式子表示为
?.
13.
如果一辆汽车从仓库出发向东行驶了
千米后到达商场,卸完货向西行驶了
千米到达加油站,那么加油站位于仓库的
?面(填方向),距仓库
?千米.
14.
填空:
()
?;
()
?;
()
?;
()
?.
15.
某计算程序是:当输入一个数时,显示的结果总等于这个数的绝对值与
的和.若输入
,则显示的结果是
?;若输入某数后,显示的结果是
,则输入的数是
?.
16.
年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循一定的规律,如表所示:
那么第
颗行星到太阳的距离是
?天文单位.
三、解答题(共3小题;共40分)
17.
数学课上李老师提出一个问题:“绝对值小于
的整数共有多少个?”王明一下子举手了,老师请他回答,王明答道:“不就是
,,,,,,,,
这九个吗.”张华认为王明的回答有错,起来补充道:“李老师,王明还漏了
,,,,,,,,,所以一共有
个.”你觉得张华的补充完整了吗?为什么?
18.
将
,,,,,,,,
这
个数分别填入如图方阵的
个空格中,使得横,竖,斜对角的
个数相加的和相等.
19.
计算:.
答案
第一部分
1.
A
【解析】根据题意,得
,
则气温由
上升了
时的气温是
.
2.
C
3.
D
4.
C
5.
B
6.
D
7.
D
8.
B
9.
A
10.
B
11.
A
第二部分
12.
结合,
13.
西,
14.
,,,
15.
,
16.
第三部分
17.
不完整,还有零,共有
个.
18.
答案不唯一,如下:
19.
第2页(共5
页)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
