二次函数的应用复习

(共23张PPT)
图中的这些图片你看到什么？
想到了数学中什么知识？
二次函数的应用复习
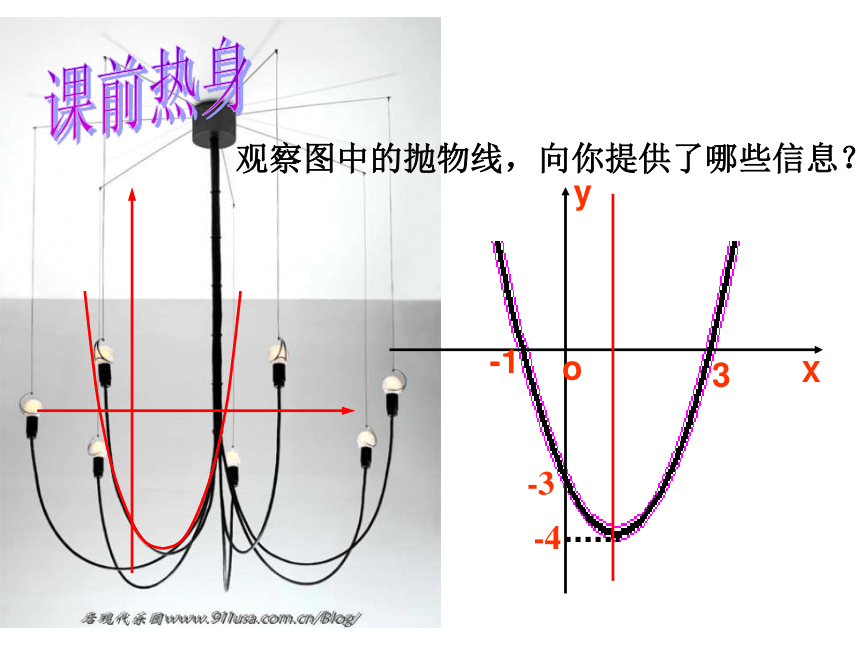
观察图中的抛物线，向你提供了哪些信息？
X
y
o
3
-1
-4
-3
如图是某公园一圆形喷水池，水流在各方向沿形状相同的抛物线落下。建立如图所示的坐标系，如果喷头所在处A（0，1.25），水流路线最高处B（1，2.25），则该抛物线的表达式为　　　　　　　　　。如果不考虑其他因素，那么水池的半径至少要　　米，才能使喷出的水流不致落到池外。
Y
O x
B(1,2.25)
．
(0,1.25) A
y= －(x-1)2 +2.25
2.5
问题1：
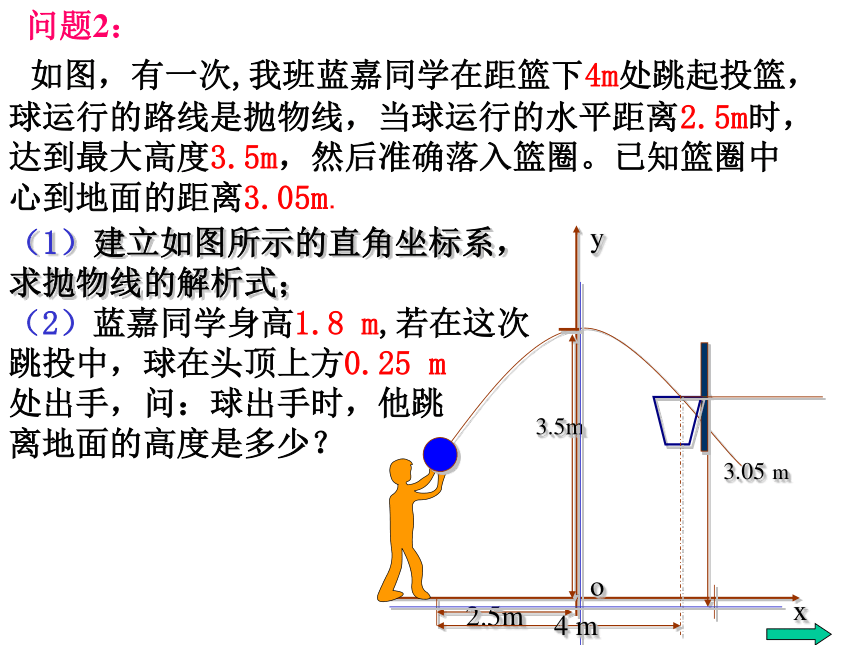
（2）蓝嘉同学身高1.8 m,若在这次跳投中，球在头顶上方0.25 m
处出手，问：球出手时，他跳
离地面的高度是多少？
x
y
o
如图，有一次,我班蓝嘉同学在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离2.5m时，达到最大高度3.5m，然后准确落入篮圈。已知篮圈中心到地面的距离3.05m.
3.05 m
2.5m
3.5m
（1）建立如图所示的直角坐标系，
求抛物线的解析式；
4 m
问题2：
解：（1）建立如图所示的直角坐标系，则球的最高点和球篮筐中心的坐标分别为(0,3.5),(1.5,3.05).
3.5=c
3.05=1.52a+c
设所求的二次函数的表达式为 y=ax2+c.
将以上两点坐标代入，得
解得
a= -02
c= 3.5
∴该抛物线的表达式为y=-0.2x2+3.5
(2)球的出手点的横坐标为-2.5，将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时，才能投中。
∴球出手时，他跳离地面的高度为
2.25-1.8-0.25=0.2m
实际问题
数学问题
求解数学问题
思路：
问题3:如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
A
B
C
D
解：
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
(2)当x＝ 时，在0S最大值＝ ＝36（平方米）
∴ S＝x（24－4x）
＝－4x2＋24 x （0∴ 0<24－4x ≤8 ， 4≤x<6此时对称轴x=3不在4≤x<6范围内，由增减性得：
∴当x＝4m时，S最大值＝32 平方米
X

8米
问题4：某商场将进价40元一个的某种商品按50元一个售出时，能卖出500个，已知这种商品每个涨价一元，销量减少10个，为赚得最大利润，售价定为多少？最大利润是多少？
分析：利润=（每件商品所获利润）× （销售件数）
设每个涨价x元， 那么
（3）销售量可以表示为
（1）销售价可以表示为
（50+x）元（x≥ 0，且为整数）
(500-10x) 个
（2）一个商品所获利润可以表示为
（50+x-40）元
（4）共获利润可以表示为
(50+x-40)(500-10x)元
小试牛刀
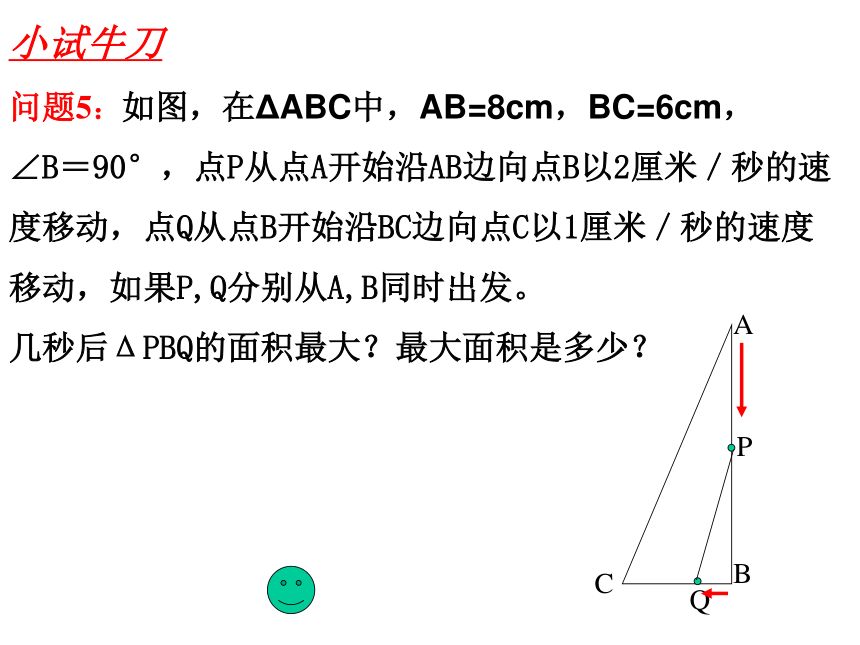
问题5：如图，在ΔABC中，AB=8cm，BC=6cm，
∠B＝90°，点P从点A开始沿AB边向点B以2厘米／秒的速度移动，点Q从点B开始沿BC边向点C以1厘米／秒的速度
移动，如果P,Q分别从A,B同时出发。
几秒后ΔPBQ的面积最大？最大面积是多少？
C
B
A
P
Q
解：根据题意，设经过x秒后ΔPBQ的面积y最大
AP=2x cm PB=（8-2x ） cm
QB=x cm
则 y=1/2 x（8-2x）
=-x2 +4x
=-（x2 -4x +4 -4）
= -（x - 2）2 + 4
所以，当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2
（0A
B
C
P
Q
在矩形荒地ABCD中，AB=10，BC=6,今在四边上分别选取E、F、G、H四点，且AE=AH=CF=CG=x，建一个花园，如何设计，可使花园面积最大？
D
C
A
B
G
H
F
E
10
6
解：设花园的面积为y
则 y=60-x2 -（10-x）（6-x）
=-2x2 + 16x
（0=-2（x-4）2 + 32
所以当x=4时 花园的最大面积为32
如图，等腰Rt△ABC中，AB＝２，点P、Q分别从A、C
两点同时出发，以相等的速度作直线运动，已知点P沿
射线AB运动，点Q沿边BC的延长线运动，PQ与直线AC
相交于点D。
(1)设AP的长为x，△PCQ的面积为S，求出
S关于x的函数关系式；
(2)当AP的长为何值时，S△PCQ= S△ABC
当P在线段AB的延长线上时
S△PCQ＝
即S＝　 (x>2）
解：（１）∵P、Q分别从A、C两点同时出发，速度相等
∴AP=CQ=x
当P在线段AB上时
S△PCQ＝
CQ PB
即S＝ 　 (0=
AP PB
(2)当S△PCQ＝S△ABC时，有
＝２
此方程无解
②　 ＝２
　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　
∴ x1=1+ , x2=1－ (舍去)
∴当AP长为1+ 时，S△PCQ＝S△ABC
问题6 若咱们这个班的全体同学利用中考前某周日，每两个同学都通过一次电话，互相鼓励，共同提高。那么咱班同学们之间共通了多少次电话？
为了解决该问题，我们可把本班人数n与通电话次数s间的关系用下列模型来表示（如图1）：
⑴若把n作为点的横坐标，s作为纵坐标，根据上述模型中的数据，在给出的平面直角坐标系图2中，描出相应各点，并用平滑的曲线连接起来；
·
·
·
·
·
⑵根据图中各点的排列规律，猜一猜上述各点会不会在某一函数的图象上？如果在，求出该函数的解析式 。
·
·
·
·
·
⑶ 根据⑵中得出的函数的关系式，求咱班同学之间共通了多少次电话。
（4）若某校初三（1）班同学之间相互共通过561次电 话，则该班有多少位同学呢？
数学建模思想
由实验获得数据
图象
函数的类别
描点法
判断或估计
根据图象和数据
待定系数法
函数关系式
实验数据
验证函数
7.如图（单位：米），等腰直角三角形ABC与正方形EFMN重叠，AB落在EF上，现将等腰直角三角形ABC以2米/秒的速度沿射线FM移动，直到AB与MN重合.设x秒时，三角形与正方形重叠部分的面积为y米2
⑴写出y与x的函数表达式及x的取值范围；
⑵画出该函数的图象；
⑶当重叠部分的面积是三角形面积
的一半时，三角形移动了多长时间？
你能利用图象来估计吗？
A（E）
B（F）
C（M）
N
10
y=-2x2+50
(0≤x≤5)
x
y
-2 -1 O 1 2 3 4 5 6 7
60
50
40
30
20
10
-10
-20
●
●
●
●
●
y=-2x2+50 (0≤x≤5)
通过本节课的学习你有什么收获？
实际问题
抽象
转化
数学问题
运用
二次函数知识
问题的解
一、根据实际问题中的抛物线，先建立平面直角坐标系，再求抛物线表达式来解决问题。
二、根据实际问题建立函数的表达式解决实际问题
总结
返回解释
检验
谢谢大家！