浙教版九年级上册数学 第2讲 二次函数的图像与性质同步学案(含答案)
文档属性
| 名称 | 浙教版九年级上册数学 第2讲 二次函数的图像与性质同步学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2讲
二次函数的图像与性质
一、课前检测
1.
若A(﹣,y1),B(-1,y2),C(,y3)为二次函数y=﹣x2-4x+5的图象上的三
点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y3<y2<y1
C.y3<y1<y2
D.y2<y1<y3
2.
对于抛物线y=﹣(x+1)2+3,下列结论:
①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);
④x>1时,y随x的增大而减小,其中正确结论的个数为( )
A.1
B.2
C.3
D.4
3.
已知二次函数y=mx2+(2m+1)x+m-1的图象与x轴有两个交点,则m的取值范围是
( )
A.m<
B.m≤
C.m>﹣且m≠0
D.m≤且m≠0
4.
已知抛物线y=x2-kx-8经过点P(2,-8),则k=__________,这条抛物线的顶点坐标
是__________.
5.
如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当-2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
二、考点梳理
考点一、二次函数的性质:
1.
二次函数y=ax2+bx+c(a≠0)有以下性质:
2.
二次函数y=ax2+bx+c的图象与x轴有没有交点由b2-4ac的符号决定:
当b2-4ac>0时,其图象与x轴有两个交点.
当b2-4ac=0时,其图象与x轴只有一个交点.
当b2-4ac<0时,其图象与x轴没有交点.
3.
二次函数的三种表达式:
(1)一般式:y=ax2+bx+c(a≠0).
(2)顶点式:y=a(x-m)2+k(a≠0).
(3)交点式:y=a(x-x1)(x-x2)(a≠0).
4.
讨论二次函数y=ax2+bx+c的增减性时,关键是抓住对称轴,分对称轴左侧(x≤﹣)
和对称轴右侧(x≥﹣)来讨论,再结合开口方向具体讨论.
三、重点突破
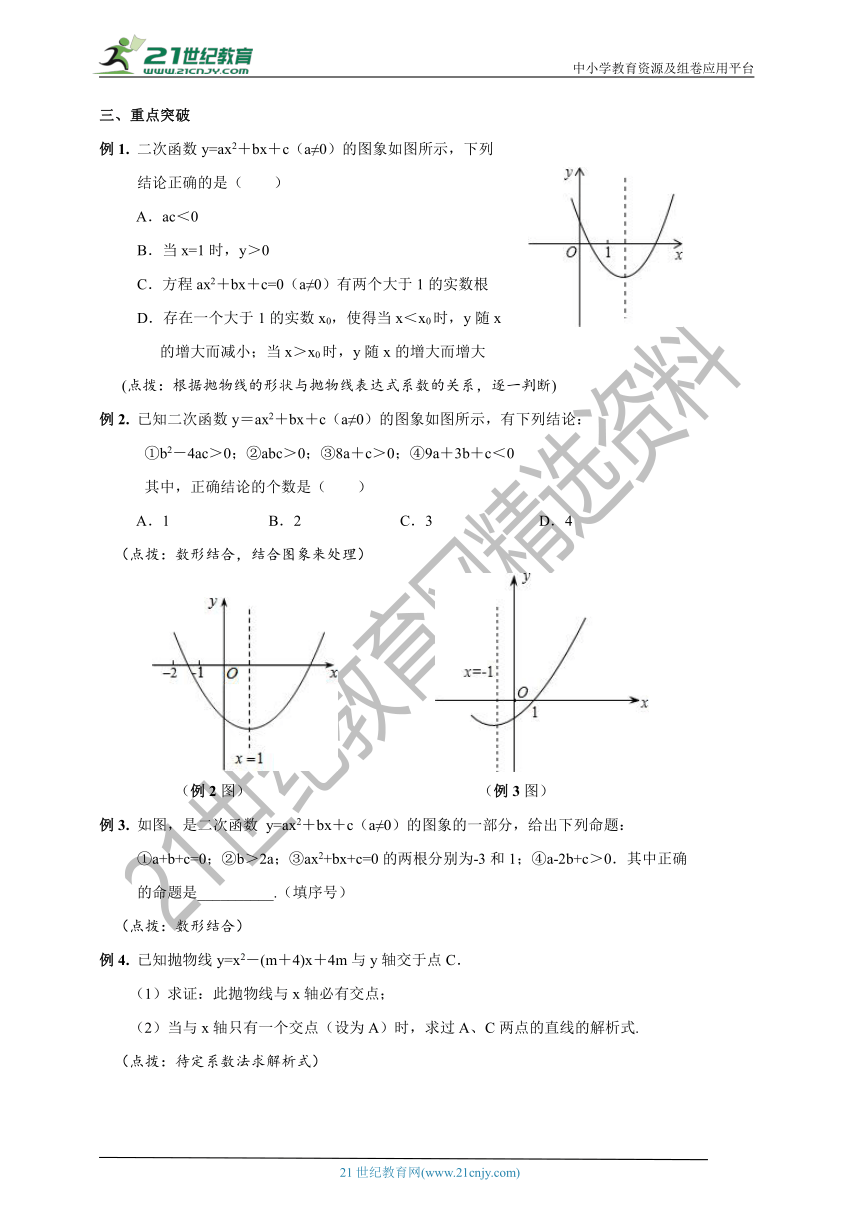
例1.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列
结论正确的是( )
A.ac<0
B.当x=1时,y>0
C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D.存在一个大于1的实数x0,使得当x<x0时,y随x
的增大而减小;当x>x0时,y随x的增大而增大
(点拨:根据抛物线的形状与抛物线表达式系数的关系,逐一判断)
例2.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0
其中,正确结论的个数是( )
A.1
B.2
C.3
D.4
(点拨:数形结合,结合图象来处理)
(例2图)
(例3图)
例3.
如图,是二次函数
y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确
的命题是__________.(填序号)
(点拨:数形结合)
例4.
已知抛物线y=x2-(m+4)x+4m与y轴交于点C.
(1)求证:此抛物线与x轴必有交点;
(2)当与x轴只有一个交点(设为A)时,求过A、C两点的直线的解析式.
(点拨:待定系数法求解析式)
例5.
已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
(点拨:注意分类讨论)
例6.
如图,一次函数y=kx+b的图象与x轴和y轴分别交于点A(﹣8,0)和点B(0,4),
线段AB的垂直平分线CD交x轴于点C,交AB于点D.
(1)求直线AB的函数表达式.
(2)求过A,B,C三点的抛物线的函数表达式.
(3)抛物线对应的二次函数有最大值还是有最小值?此时x等于多少?相应的最大值
或最小值是多少?
(点拨:二次函数的性质)
例7.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)直接写出x2+bx+c>x+m的解.
(点拨:待定系数法求函数解析式)
例8.已知二次函数y=x2-2x-8.
(1)求二次函数的顶点坐标,对称轴,最值;
(2)当x在什么范围内,y随x的增大而减小;
(3)把二次函数y=x2-2x-8向左平移三个单位长度,再向下平移四个单位长度得到的函
数解析式是什么?
(4)二次函数y=x2-2x-8与二次函数___________________关于y轴对称.
(点拨:二次函数图象与性质)
例9.已知函数y=(m-1)x2+2x+m.
(1)若该函数图象与x轴只有一个交点,求m的值.
(2)若该函数图象与坐标轴有两个交点,求m的值.
(点拨:分类讨论要周全,不重不漏)
例10.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三
点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大
于二次函数的值.
(点拨:(3)画出图象,再根据图象直接得出答案)
四、经典练习
A组
(一)选择题(共4小题)
1.
二次函数y=x2+2x-5有( )
A.最大值﹣5
B.最小值﹣5
C.最大值﹣6
D.最小值﹣6
2.
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直
线x=1,则下列结论正确的是( )
A.ac>0
B.方程ax2+bx+c=0的两个根是x1=-1,x2=3
C.2a-b=0
D.当x>0时,y随x的增大而增大
3.
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,
且x1≠x2,x1+x2=2.其中正确的有( )
A.①②③
B.②④
C.②⑤
D.②③⑤
4.
不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )
A.在y=x直线上
B.在直线y=﹣x上
C.在x轴上
D.在y轴上
(二)
填空题(共3小题)
5.
如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B
(3,
0),则由图象可知,不等式ax2+bx+c>0的解集是_____________.
(第5题图)
(第7题图)
6.
已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值
范围是__________.
7.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直
线交抛物线y=x2于点B、C,则BC的长为__________.
(三)解答题(共3小题)
8.
已知抛物线y=x2-4x+m-1.
(1)若抛物线与x轴只有一个交点,求m的值;
(2)若抛物线与直线y=2x-m只有一个交点,求m的值.
9.
已知开口向上的抛物线y=ax2-2x+|a|-4经过点(0,-3).
(1)确定此抛物线的解析式;
(2)当x取何值时,y有最小值,并求出这个最小值.
10.
如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=8,点D在BC上运动(不运动至B,C),
DE∥AC,交AB于E,=.设BD=x,△ADE的面积为y.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)x为何值时,△ADE的面积最大?最大面积是多少?
B组
(一)选择题(共4小题)
1.
若有二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x=x1+x2时,
函数值为( )
A.a+c
B.a-c
C.-c
D.c
2.
二次函数y=x2-x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a-1时,
函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
3.
如图,抛物线y1=a(x+2)2?3与y2=(x?3)2+1交于点A(1,3)过点A作x轴的平行线,
分别交两条抛物线于点B、C,则以下结论:
①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;
其中,结论正确的是( )
A.①②
B.②③
C.③④
D.①④
4.
对于抛物线y=﹣4x+x2-7,有下列说法:①抛物线的开口向上.②对称轴为x=2.③顶
点坐标为(2,-3).④点(﹣,-9)在抛物线上.⑤抛物线与x轴有两个交点,其中
正确的有( )
A.1个
B.2个
C.3个
D.4个
(二)填空题(共3小题)
5.
如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶
点A、B、C,则ac的值是__________.
6.
已知抛物线y=x2-2x-3的图象与x轴交于A,B两点,在x轴上方的抛物线上有一点C,
使△ABC的面积为10,则C点坐标为__________.
7.
抛物线y=(m-1)x2+2x+m图象与坐标轴有且只有2个交点,则m=__________.
(三)解答题(共3小题)
8.
已知二次函数y有最大值4,且图象与x轴两交点间的距离是8,对称轴为x=-3,求此
二次函数的解析式.
9.
若函数y=3x2-(9+a)x+6+2a(x是自变量且x为整数),在x=6或x=7时取得最小
值,求a的取值范围.
10.
已知二次函数y=x2+bx-3的图象经过点P(-2,5).
(1)求b的值并写出当1<x≤3时y的取值范围;
(2)设P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图象上,
①当m=4时,y1、y2、y3能否作为同一个三角形三边的长?请说明理由;
②当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,
请说明理由.
五、优化提高
1.
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,
-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是(,);
②当m>0时,函数图象截x轴所得的线段长度大于;
③当m<0时,函数在x>时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④
B.①②④
C.①③④
D.②④
2.
已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构
成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图
象.它们的顶点在一条直线上,这条直线的解析式是y=____________________.
3.
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x
…
-1
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
(1)求该二次函数的关系式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,试比较y1与y2
的大小.
4.
已知:关于x的方程ax2-(1-3a)x+2a-1=0.
(1)当a取何值时,二次函数y=ax2-(1-3a)x+2a-1的对称轴是x=-2;
(2)求证:a取任何实数时,方程ax2-(1-3a)x+2a-1=0总有实数根.
5.
已知抛物线y=ax2+bx+c与y轴交于点(0,3a),对称轴为x=1.
(1)试用含a的代数式表示b、c.
(2)当抛物线与直线y=x-1交于点(2,1)时,求此抛物线的解析式.
(3)求当b(c+6)取得最大值时的抛物线的顶点坐标.
参考答案
一、课前检测
1.
C
【解答】∵二次函数y=-x2-4x+5中a=-1<0,
∴抛物线开口向下,对称轴为x=﹣=﹣=﹣2,
∵B(-1,y2),C(,y3)中横坐标均大于-2,
∴它们在对称轴的右侧y3<y2,
∵A(﹣,y1)中横坐标小于-2,
∴它在对称轴的左侧,
而它关于x=-2的对称点为2×(-2)-(﹣)=﹣,>﹣>-1,
∵a<0时,抛物线开口向下,在对称轴的右侧y随x的增大而减小,∴y3<y1<y2.
2.
C
3.
C
【分析】根据二次函数y=mx2+(2m+1)x+m-1的图象与x轴有两个交点,可得
△=(2m+1)2-4m×(m-1)>0且m≠0.
4.
2
(1,-9)
5.(1)将A(-1,0),B(0,-3),C(4,5)代入y=ax2+bx+c中,得
a?b+c=0
c=?3
16a+4b+c=5
解得a=1,b=?2,c=?3,
∴抛物线解析式为:y=x2-2x-3,即y=(x-1)2-4,顶点坐标为(1,-4).
(2)∵对称轴x=1,开口向上,
∴当-2<x<2时,y有最小值为-4,
x=-2时,对应点离对称轴较远,函数有最大值为5,∴-4≤y<5.
(3)∵抛物线经过A(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点为(3,0),
又抛物线开口向上,
∴当x>3或x<-1时,y>0.
三、重点突破
例1.
D
【解答】A、抛物线开口向上,a>0,抛物线与y轴交于正半轴,c>0,所以ac>0,错误;
B、由图象可知,当x=1时,y<0,错误;
C、方程ax2+bx+c=0(a≠0)有一个根小于1,一个根大于1,错误;
D、由于函数图象的对称轴在x=1的右侧,所以存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大,正确.
例2.
D
【解答】①由图知抛物线与x轴有两个不同的交点,则△=b2-4ac>0,故①正确;
②抛物线开口向上,得:a>0;抛物线的对称轴为x=﹣=1,b=-2a,故b<0;
抛物线交y轴于负半轴,得:c<0;∴abc>0;故②正确;
③根据②可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故③正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确.
例3.
①③
【分析】由图象可知过(1,0),代入得到a+b+c=0;根据﹣=-1,推出b=2a;根据图象关于对称轴对称,得出与X轴的交点是(-3,0),(1,0);由a-2b+c=a-2b-a-b=-3b<0,根据结论判断即可.
例4.(1)证明:∵△=(m+4)2-16m=(m-4)2,∴△≥0,∴此抛物线与x轴必有交点.
(2)当只有一个交点时,m=4,解析式为y=x2-8x+16,∴A(4,0),C(0,16),
设直线AC为y=kx+16,∴k=-4,即直线AC为y=-4x+16.
例5.(1)当x=0时,y=1.
∴不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1).
(2)①当m=0时,函数y=mx2-6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+1的图象与x轴只有一个交点,则方程mx2-6x+1=0有两个相等的实数根,∴△=(-6)2-4m=0,m=9.
综上,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或9.
例6.
(1)由题意得,
-8k+b=0
b=4,
解得,k=,b=4,∴直线AB的函数表达式为y=x+4.
(2)连结BC,设OC=x,∵OA=8,∴AC=8-x,
∵在Rt△BOC中,OB=4,OC=x,BC=AC=8-x,∴x2+42=(8-x)2,解得x=3,
∴点C的坐标为(-3,0).
设所求抛物线的函数表达式为y=a(x-x1)(x-x2)(a≠0),
∵抛物线过点A(-8,0),C(-3,0),∴y=a(x+8)(x+3)(a≠0),
∵抛物线过点B(0,4),∴4=a(0+8)(0+3),解得a=,∴y=(x+8)(x+3),即y=x2+x+4.
(3)∵a=>0,∴抛物线对应的二次函数有最小值,当x=﹣=﹣时,y最小=﹣.
例7.(1)把点A(1,0),B(3,2)分别代入直线y=x+m和抛物线y=x2+bx+c得:
0=1+m,
0=1+b+c
2=9+3b+c
∴m=-1,b=-3,c=2,
∴y=x-1,y=x2-3x+2.
(2)x2-3x+2>x-1,解得:x<1或x>3.
例8.(1)顶点(1,-9);对称轴:直线x=1;最小值:-9
(2)x≤1
(3)y=(x+2)2-13
(4)y=x2+2x-8
例9.(1)当m-1=0时,函数y=2x+1的图象为一条直线,与x轴只有一个交点,
∴m=1符合题意.
当m-1≠0,图象为抛物线,
∴△=4-4m(m-1)=0,解得m1=
EQ
\F(1+,2),m2=
EQ
\F(1-,2),
综上,当m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,函数y=(m-1)x2+2x+m与x轴只有一个交点.
(2)同(1),m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,
函数y=(m-1)x2+2x+m与x轴有一个交点,与y轴有一个交点.
∴m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,与坐标轴有两个交点.
当m=0时,y=﹣x2+2x与x轴交于(0,0),(2,0)两点,与y轴交于(0,0),
∴与坐标轴有两个交点
综上,m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)或m=0时,图象与坐标轴有两个交点.
例10.(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
∴
4a+2b+c=0
c=?1
16a+4b+c=5
∴a=,b=﹣,c=﹣1,
∴二次函数的解析式为y=x2-x-1.
(2)当y=0时,得x2-x-1,
解得x1=2,x2=-1,∴点D坐标为(-1,0).
(3)图象如图,
当一次函数的值大于二次函数的值时,
x的取值范围是-1<x<4.
四、经典练习
A组
1.
D
2.
B
【解答】A、抛物线开口向上,则a>0,抛物线与y轴的交点在x轴下方,则c<0,所以ac<0,所以A选项错误;
B、抛物线的对称轴为直线x=1,点(3,0)关于直线x=1的对称点为(-1,0),则方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以B选项正确;
C、抛物线的对称轴为直线x=﹣=1,则b=-2a,即2a+b=0,所以C选项错误;
D、当0<x<1,y随x的增大而减小;x>1时,y随x的增大而增大,所以D选项错误.
3.
D
【分析】根据抛物线开口方向得a<0,由抛物线对称轴为直线x=﹣
=1,得到b=-2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)的右侧,则当x=-1时,y<0,所以a-b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1-x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=-﹣,然后把b=-2a代入计算得到x1+x2=2.
4.
B
【分析】直接利用配方法可求顶点坐标为(-m,m),即可判断顶点所在直线.
5.
x<-1或x>3
【分析】由抛物线与x轴的一个交点(3,0)和对称轴x=1可以确定另一交点坐标为(-1,0),又y=ax2+bx+c>0时,图象在x轴上方,由此可求x的取值范围.
6.
m≥-2
【分析】根据二次函数性质,利用二次函数的对称轴不大于2列式计算即可得解.
7.
6
【解答】∵抛物线y=ax2+3与y轴交于点A,∴A点坐标为(0,3).
当y=3时,
x2=3,解得x=±3,∴B点坐标为(-3,3),C点坐标为(3,3),
∴BC=3-(-3)=6.
8.(1)∵函数y=x2-4x+m-1,抛物线与x轴只有一个交点,
∴b2-4ac=16-4(m-1)=20-4m=0,解得:m=5.
(2)联立抛物线与直线解析式消掉y得,x2-4x+m-1=2x-m,整理得,x2-6x+2m-1=0,
∵抛物线与直线只有一个交点,∴△=b2-4ac=(-6)2-4×1×(2m-1)=0,解得m=5.
9.(1)由抛物线过(0,-3),得:-3=|a|-4,∴|a|=1,即a=±1.
∵抛物线开口向上,∴a=1,∴抛物线的解析式为y=x2-2x-3.
(2)∵y=x2-2x-3=(x-1)2-4,∴当x=1时,y有最小值-4.
10.(1)∵=,设BD=x,∴DE=x,
设△ADE中DE边上的高为h,∵DE∥AC,∴h=CD=BC-BD=8-x,
∴y=DE?CD=×x?(8-x),即y=﹣x2+3x.
自变量x的取值范围是0<x<8.
(2)x=﹣
EQ
\F(3,2×(﹣))=4时,y最大==6,即当x=4时,△ADE的面积最大为6.
B组
1.
D
【解答】二次函数y=ax2+c的对称轴是y轴,当x取x1,x2(x1≠x2)时,函数值相等,即以x1,x2为横坐标的点关于y轴对称,则x1+x2=0,此时函数值为y=ax2+c=0+c=c.
2.
C
【解答】∵对称轴是x=,0<x1<,故由对称性<x2<1,
当x=a时,y<0,则a的范围是x1<a<x2,∴a-1<0,当x<时y随x的增大而减小,
当x=0时函数值是m.因而当x=a-1<0时,函数值y一定大于m.
3.
D
【解答】①∵抛物线y2=(x-3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=,故本小题错误;
③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=(x+2)2-3,
当x=0时,y1=(0+2)2-3=﹣,y2=(0-3)2+1=,故y2-y1=+=,故本小题错误;
④∵物线y1=a(x+2)2-3与y2=(x-3)2+1交于点A(1,3),
∴y1的对称轴为x=-2,y2的对称轴为x=3,∴B(-5,3),C(5,3)
∴AB=6,AC=4,∴2AB=3AC,故本小题正确.
4.
C
【解答】抛物线y=-4x+x2-7可化为y=(x-2)2-11的形式,
①因为抛物线y=-4x+x2-7中,a=1>0,所以抛物线开口向上,故本小题正确;
②由抛物线顶点式可知,其对称轴方程是x=2,故本小题正确;
③由抛物线顶点式可知,其顶点坐标是(2,-11),故本小题错误;
④当x=﹣时,y=(﹣-2)2-11=﹣,故本小题错误.
⑤因为△=(-4)2-4×1×(-7)=44>0,所以抛物线与x轴有两个不同的交点,故正确.
5.﹣2
【解答】设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=﹣,则ac=﹣?2m=-2.
6.
(4,5)或(-2,5)
【解答】由x2-2x-3=0得x1=3,x2=-1,∴AB距离为4,
要使△ABC的面积为10,C的纵坐标应为5,
把y=5时代入函数y=x2-2x-3得x2-2x-3=5,解得x1=4,x2=-2.
∴C点坐标为(4,5)或(-2,5).
7.
-1或2或0
【解答】∵抛物线y=(m-1)x2+2x+m图象与坐标轴有且只有2个交点,
而抛物线与y轴始终有一个交点,∴与x轴只有一个交点,
∴△=4-2(m-1)m=0,∴m=-1或2;
另外当m=0时,y=-x2+2x与x轴的一个交点(0,0)正好是与y轴的交点,即此时也与坐标轴只有两个交点.
综上,m=-1或2或0.
8.y=﹣(x+7)(x-1)
【解答】∵该函数图象与x轴两交点间的距离是8,对称轴为x=-3,
∴抛物线与x轴的两个交点坐标是(-7,0)、(1,0).
故设该抛物线解析式为y=a(x+7)(x-1)(a≠0).
把顶点(-3,4)代入得到:4=a(-3+7)(-3-1),解得a=﹣.
则该二次函数解析式为:y=﹣(x+7)(x-1).
9.24<a<36
【解答】抛物线的对称轴为直线x=﹣=,
∵在x=6或x=7时取得最小值,x是整数,
∴
>5.5①
<7.5②,
解不等式①得,a>24,解不等式②得,a<36,
∴不等式组的解是24<a<36,即a的取值范围是24<a<36.
10.(1)把(-2,5)代入二次函数y=x2+bx-3得:5=4-2b-3,∴b=-2,
∴y=x2-2x-3=(x-1)2-4,∴抛物线的开口方向向上,对称轴是直线x=1,
把x=1代入得y=-4,x=3代入得y=0,∴当1<x≤3时y取值范围是-4<y≤0.
(2)①当m=4时,y1、y2、y3不能作为同一个三角形三边的长.
理由是当m=4时,P1(4,y1)、P2(5,y2)、P3(6,y3),
代入抛物线的解析式得:y1=5,y2=12,y3=21,
∵5+12<21,∴当m=4时,y1、y2、y3不能作为同一个三角形三边的长.
②理由是:∵把P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)代入y=x2-2x-3=(x-1)2-4得:∴y1=(m-1)2-4,y2=(m+1-1)2-4,y3=(m+2-1)2-4,
∴y1+y2-y3=(m-1)2-4+(m+1-1)2-4-[(m+2-1)2-4]=(m-2)2-8,
∵m≥5,∴(m-2)2-8>0,∴y1+y2>y3,
根据三角形的三边关系定理:三角形的任意两边之和大于第三边(也可求出两小边的和大于第三边),
∴当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长.
五、优化提高
1.
B
【解答】根据定义可得函数y=2mx2+(1-m)x+(-1-m),
①当m=-3时,函数解析式为y=-6x2+4x+2,
∴﹣=﹣=,
==,∴顶点坐标是(,),正确.
②函数y=2mx2+(1-m)x+(-1-m)与x轴两交点坐标为(1,0),(﹣,0),
当m>0时,1-(﹣)=+>,正确;
③当m<0时,函数y=2mx2+(1-m)x+(-1-m)开口向下,对称轴x=->,
∴x可能在对称轴左侧也可能在对称轴右侧,错误;
④y=2mx2+(1-m)x+(-1-m)=m(2x2-x-1)+x-1,若使函数图象恒经过一点,m≠0时,应使2x2-x-1=0,可得x1=1,x2=﹣,当x=1时,y=0,当x=﹣时,y=﹣,则函数一定经过点(1,0)和(﹣,﹣),正确.
2.
x?1
【解答】由已知得抛物线顶点坐标为(2a,a-1),
设x=2a①,y=a-1②,
①-②×2,消去a得,x-2y=2,即y=x-1.
3.(1)根据题意,当x=0时,y=5;当x=1时,y=2;
∴
5=c
2=1+b+c
解得b=?4,c=5,∴该二次函数关系式为y=x2-4x+5.
(2)∵y=x2-4x+5=(x-2)2+1,
∴当x=2时,y有最小值,最小值是1.
(3)∵A(m,y1),B(m+1,y2)两点都在函数y=x2-4x+5的图象上,
∴y1=m2-4m+5,y2=(m+1)2-4(m+1)+5=m2-2m+2,
y2-y1=(m2-2m+2)-(m2-4m+5)=2m-3,
∴①当2m-3<0,即m<时,y1>y2;
②当2m-3=0,即m=时,y1=y2;
③当2m-3>0,即m>时,y1<y2.
4.
(1)当对称轴是x=-2,
∴x=﹣==-2,解得:a=-1.
(2)①当a=0时,方程为一元一次方程,方程ax2-(1-3a)x+2a-1=0有一个实数根.
②∵当a≠0时,方程为一元二次方程,
∴△=[-(1-3a)]2-4a(2a-1)=a2-2a+1=(a-1)2≥0,
∴方程有实数根,
∴a取任何实数时,方程ax2-(1-3a)x+2a-1=0总有实数根.
5.(1)∵抛物线与y轴交于点(0,3a),∴c=3a,
∵对称轴为=1,∴x=﹣=1,∴b=-2a.
(2)∵抛物线与直线y=x-1交于点(2,1),
∴(2,1)在抛物线上,
∴1=a×22+2(-2a)+3a,∴a=,
∴b=﹣2a=﹣,c=3a=1,
∴抛物线为y=x2-x+1.
(3)∵b(c+6)=﹣2a(3a+6)=﹣6a2-12a=﹣6(a+1)2+6,
当a=﹣1时,b(c+6)的最大值为6;
∴抛物线y=﹣x2+2x-3=﹣(x-1)2-2,故抛物线的顶点坐标为(1,-2).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第2讲
二次函数的图像与性质
一、课前检测
1.
若A(﹣,y1),B(-1,y2),C(,y3)为二次函数y=﹣x2-4x+5的图象上的三
点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y3<y2<y1
C.y3<y1<y2
D.y2<y1<y3
2.
对于抛物线y=﹣(x+1)2+3,下列结论:
①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);
④x>1时,y随x的增大而减小,其中正确结论的个数为( )
A.1
B.2
C.3
D.4
3.
已知二次函数y=mx2+(2m+1)x+m-1的图象与x轴有两个交点,则m的取值范围是
( )
A.m<
B.m≤
C.m>﹣且m≠0
D.m≤且m≠0
4.
已知抛物线y=x2-kx-8经过点P(2,-8),则k=__________,这条抛物线的顶点坐标
是__________.
5.
如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当-2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
二、考点梳理
考点一、二次函数的性质:
1.
二次函数y=ax2+bx+c(a≠0)有以下性质:
2.
二次函数y=ax2+bx+c的图象与x轴有没有交点由b2-4ac的符号决定:
当b2-4ac>0时,其图象与x轴有两个交点.
当b2-4ac=0时,其图象与x轴只有一个交点.
当b2-4ac<0时,其图象与x轴没有交点.
3.
二次函数的三种表达式:
(1)一般式:y=ax2+bx+c(a≠0).
(2)顶点式:y=a(x-m)2+k(a≠0).
(3)交点式:y=a(x-x1)(x-x2)(a≠0).
4.
讨论二次函数y=ax2+bx+c的增减性时,关键是抓住对称轴,分对称轴左侧(x≤﹣)
和对称轴右侧(x≥﹣)来讨论,再结合开口方向具体讨论.
三、重点突破
例1.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列
结论正确的是( )
A.ac<0
B.当x=1时,y>0
C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D.存在一个大于1的实数x0,使得当x<x0时,y随x
的增大而减小;当x>x0时,y随x的增大而增大
(点拨:根据抛物线的形状与抛物线表达式系数的关系,逐一判断)
例2.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0
其中,正确结论的个数是( )
A.1
B.2
C.3
D.4
(点拨:数形结合,结合图象来处理)
(例2图)
(例3图)
例3.
如图,是二次函数
y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确
的命题是__________.(填序号)
(点拨:数形结合)
例4.
已知抛物线y=x2-(m+4)x+4m与y轴交于点C.
(1)求证:此抛物线与x轴必有交点;
(2)当与x轴只有一个交点(设为A)时,求过A、C两点的直线的解析式.
(点拨:待定系数法求解析式)
例5.
已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
(点拨:注意分类讨论)
例6.
如图,一次函数y=kx+b的图象与x轴和y轴分别交于点A(﹣8,0)和点B(0,4),
线段AB的垂直平分线CD交x轴于点C,交AB于点D.
(1)求直线AB的函数表达式.
(2)求过A,B,C三点的抛物线的函数表达式.
(3)抛物线对应的二次函数有最大值还是有最小值?此时x等于多少?相应的最大值
或最小值是多少?
(点拨:二次函数的性质)
例7.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)直接写出x2+bx+c>x+m的解.
(点拨:待定系数法求函数解析式)
例8.已知二次函数y=x2-2x-8.
(1)求二次函数的顶点坐标,对称轴,最值;
(2)当x在什么范围内,y随x的增大而减小;
(3)把二次函数y=x2-2x-8向左平移三个单位长度,再向下平移四个单位长度得到的函
数解析式是什么?
(4)二次函数y=x2-2x-8与二次函数___________________关于y轴对称.
(点拨:二次函数图象与性质)
例9.已知函数y=(m-1)x2+2x+m.
(1)若该函数图象与x轴只有一个交点,求m的值.
(2)若该函数图象与坐标轴有两个交点,求m的值.
(点拨:分类讨论要周全,不重不漏)
例10.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三
点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大
于二次函数的值.
(点拨:(3)画出图象,再根据图象直接得出答案)
四、经典练习
A组
(一)选择题(共4小题)
1.
二次函数y=x2+2x-5有( )
A.最大值﹣5
B.最小值﹣5
C.最大值﹣6
D.最小值﹣6
2.
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直
线x=1,则下列结论正确的是( )
A.ac>0
B.方程ax2+bx+c=0的两个根是x1=-1,x2=3
C.2a-b=0
D.当x>0时,y随x的增大而增大
3.
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,
且x1≠x2,x1+x2=2.其中正确的有( )
A.①②③
B.②④
C.②⑤
D.②③⑤
4.
不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )
A.在y=x直线上
B.在直线y=﹣x上
C.在x轴上
D.在y轴上
(二)
填空题(共3小题)
5.
如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B
(3,
0),则由图象可知,不等式ax2+bx+c>0的解集是_____________.
(第5题图)
(第7题图)
6.
已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值
范围是__________.
7.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直
线交抛物线y=x2于点B、C,则BC的长为__________.
(三)解答题(共3小题)
8.
已知抛物线y=x2-4x+m-1.
(1)若抛物线与x轴只有一个交点,求m的值;
(2)若抛物线与直线y=2x-m只有一个交点,求m的值.
9.
已知开口向上的抛物线y=ax2-2x+|a|-4经过点(0,-3).
(1)确定此抛物线的解析式;
(2)当x取何值时,y有最小值,并求出这个最小值.
10.
如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=8,点D在BC上运动(不运动至B,C),
DE∥AC,交AB于E,=.设BD=x,△ADE的面积为y.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)x为何值时,△ADE的面积最大?最大面积是多少?
B组
(一)选择题(共4小题)
1.
若有二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x=x1+x2时,
函数值为( )
A.a+c
B.a-c
C.-c
D.c
2.
二次函数y=x2-x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a-1时,
函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
3.
如图,抛物线y1=a(x+2)2?3与y2=(x?3)2+1交于点A(1,3)过点A作x轴的平行线,
分别交两条抛物线于点B、C,则以下结论:
①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;
其中,结论正确的是( )
A.①②
B.②③
C.③④
D.①④
4.
对于抛物线y=﹣4x+x2-7,有下列说法:①抛物线的开口向上.②对称轴为x=2.③顶
点坐标为(2,-3).④点(﹣,-9)在抛物线上.⑤抛物线与x轴有两个交点,其中
正确的有( )
A.1个
B.2个
C.3个
D.4个
(二)填空题(共3小题)
5.
如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过正方形ABOC的三个顶
点A、B、C,则ac的值是__________.
6.
已知抛物线y=x2-2x-3的图象与x轴交于A,B两点,在x轴上方的抛物线上有一点C,
使△ABC的面积为10,则C点坐标为__________.
7.
抛物线y=(m-1)x2+2x+m图象与坐标轴有且只有2个交点,则m=__________.
(三)解答题(共3小题)
8.
已知二次函数y有最大值4,且图象与x轴两交点间的距离是8,对称轴为x=-3,求此
二次函数的解析式.
9.
若函数y=3x2-(9+a)x+6+2a(x是自变量且x为整数),在x=6或x=7时取得最小
值,求a的取值范围.
10.
已知二次函数y=x2+bx-3的图象经过点P(-2,5).
(1)求b的值并写出当1<x≤3时y的取值范围;
(2)设P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图象上,
①当m=4时,y1、y2、y3能否作为同一个三角形三边的长?请说明理由;
②当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,
请说明理由.
五、优化提高
1.
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,
-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是(,);
②当m>0时,函数图象截x轴所得的线段长度大于;
③当m<0时,函数在x>时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④
B.①②④
C.①③④
D.②④
2.
已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构
成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图
象.它们的顶点在一条直线上,这条直线的解析式是y=____________________.
3.
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x
…
-1
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
(1)求该二次函数的关系式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,试比较y1与y2
的大小.
4.
已知:关于x的方程ax2-(1-3a)x+2a-1=0.
(1)当a取何值时,二次函数y=ax2-(1-3a)x+2a-1的对称轴是x=-2;
(2)求证:a取任何实数时,方程ax2-(1-3a)x+2a-1=0总有实数根.
5.
已知抛物线y=ax2+bx+c与y轴交于点(0,3a),对称轴为x=1.
(1)试用含a的代数式表示b、c.
(2)当抛物线与直线y=x-1交于点(2,1)时,求此抛物线的解析式.
(3)求当b(c+6)取得最大值时的抛物线的顶点坐标.
参考答案
一、课前检测
1.
C
【解答】∵二次函数y=-x2-4x+5中a=-1<0,
∴抛物线开口向下,对称轴为x=﹣=﹣=﹣2,
∵B(-1,y2),C(,y3)中横坐标均大于-2,
∴它们在对称轴的右侧y3<y2,
∵A(﹣,y1)中横坐标小于-2,
∴它在对称轴的左侧,
而它关于x=-2的对称点为2×(-2)-(﹣)=﹣,>﹣>-1,
∵a<0时,抛物线开口向下,在对称轴的右侧y随x的增大而减小,∴y3<y1<y2.
2.
C
3.
C
【分析】根据二次函数y=mx2+(2m+1)x+m-1的图象与x轴有两个交点,可得
△=(2m+1)2-4m×(m-1)>0且m≠0.
4.
2
(1,-9)
5.(1)将A(-1,0),B(0,-3),C(4,5)代入y=ax2+bx+c中,得
a?b+c=0
c=?3
16a+4b+c=5
解得a=1,b=?2,c=?3,
∴抛物线解析式为:y=x2-2x-3,即y=(x-1)2-4,顶点坐标为(1,-4).
(2)∵对称轴x=1,开口向上,
∴当-2<x<2时,y有最小值为-4,
x=-2时,对应点离对称轴较远,函数有最大值为5,∴-4≤y<5.
(3)∵抛物线经过A(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点为(3,0),
又抛物线开口向上,
∴当x>3或x<-1时,y>0.
三、重点突破
例1.
D
【解答】A、抛物线开口向上,a>0,抛物线与y轴交于正半轴,c>0,所以ac>0,错误;
B、由图象可知,当x=1时,y<0,错误;
C、方程ax2+bx+c=0(a≠0)有一个根小于1,一个根大于1,错误;
D、由于函数图象的对称轴在x=1的右侧,所以存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大,正确.
例2.
D
【解答】①由图知抛物线与x轴有两个不同的交点,则△=b2-4ac>0,故①正确;
②抛物线开口向上,得:a>0;抛物线的对称轴为x=﹣=1,b=-2a,故b<0;
抛物线交y轴于负半轴,得:c<0;∴abc>0;故②正确;
③根据②可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故③正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确.
例3.
①③
【分析】由图象可知过(1,0),代入得到a+b+c=0;根据﹣=-1,推出b=2a;根据图象关于对称轴对称,得出与X轴的交点是(-3,0),(1,0);由a-2b+c=a-2b-a-b=-3b<0,根据结论判断即可.
例4.(1)证明:∵△=(m+4)2-16m=(m-4)2,∴△≥0,∴此抛物线与x轴必有交点.
(2)当只有一个交点时,m=4,解析式为y=x2-8x+16,∴A(4,0),C(0,16),
设直线AC为y=kx+16,∴k=-4,即直线AC为y=-4x+16.
例5.(1)当x=0时,y=1.
∴不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1).
(2)①当m=0时,函数y=mx2-6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+1的图象与x轴只有一个交点,则方程mx2-6x+1=0有两个相等的实数根,∴△=(-6)2-4m=0,m=9.
综上,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或9.
例6.
(1)由题意得,
-8k+b=0
b=4,
解得,k=,b=4,∴直线AB的函数表达式为y=x+4.
(2)连结BC,设OC=x,∵OA=8,∴AC=8-x,
∵在Rt△BOC中,OB=4,OC=x,BC=AC=8-x,∴x2+42=(8-x)2,解得x=3,
∴点C的坐标为(-3,0).
设所求抛物线的函数表达式为y=a(x-x1)(x-x2)(a≠0),
∵抛物线过点A(-8,0),C(-3,0),∴y=a(x+8)(x+3)(a≠0),
∵抛物线过点B(0,4),∴4=a(0+8)(0+3),解得a=,∴y=(x+8)(x+3),即y=x2+x+4.
(3)∵a=>0,∴抛物线对应的二次函数有最小值,当x=﹣=﹣时,y最小=﹣.
例7.(1)把点A(1,0),B(3,2)分别代入直线y=x+m和抛物线y=x2+bx+c得:
0=1+m,
0=1+b+c
2=9+3b+c
∴m=-1,b=-3,c=2,
∴y=x-1,y=x2-3x+2.
(2)x2-3x+2>x-1,解得:x<1或x>3.
例8.(1)顶点(1,-9);对称轴:直线x=1;最小值:-9
(2)x≤1
(3)y=(x+2)2-13
(4)y=x2+2x-8
例9.(1)当m-1=0时,函数y=2x+1的图象为一条直线,与x轴只有一个交点,
∴m=1符合题意.
当m-1≠0,图象为抛物线,
∴△=4-4m(m-1)=0,解得m1=
EQ
\F(1+,2),m2=
EQ
\F(1-,2),
综上,当m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,函数y=(m-1)x2+2x+m与x轴只有一个交点.
(2)同(1),m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,
函数y=(m-1)x2+2x+m与x轴有一个交点,与y轴有一个交点.
∴m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)时,与坐标轴有两个交点.
当m=0时,y=﹣x2+2x与x轴交于(0,0),(2,0)两点,与y轴交于(0,0),
∴与坐标轴有两个交点
综上,m=1或
EQ
\F(1+,2)或
EQ
\F(1-,2)或m=0时,图象与坐标轴有两个交点.
例10.(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
∴
4a+2b+c=0
c=?1
16a+4b+c=5
∴a=,b=﹣,c=﹣1,
∴二次函数的解析式为y=x2-x-1.
(2)当y=0时,得x2-x-1,
解得x1=2,x2=-1,∴点D坐标为(-1,0).
(3)图象如图,
当一次函数的值大于二次函数的值时,
x的取值范围是-1<x<4.
四、经典练习
A组
1.
D
2.
B
【解答】A、抛物线开口向上,则a>0,抛物线与y轴的交点在x轴下方,则c<0,所以ac<0,所以A选项错误;
B、抛物线的对称轴为直线x=1,点(3,0)关于直线x=1的对称点为(-1,0),则方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以B选项正确;
C、抛物线的对称轴为直线x=﹣=1,则b=-2a,即2a+b=0,所以C选项错误;
D、当0<x<1,y随x的增大而减小;x>1时,y随x的增大而增大,所以D选项错误.
3.
D
【分析】根据抛物线开口方向得a<0,由抛物线对称轴为直线x=﹣
=1,得到b=-2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)的右侧,则当x=-1时,y<0,所以a-b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1-x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=-﹣,然后把b=-2a代入计算得到x1+x2=2.
4.
B
【分析】直接利用配方法可求顶点坐标为(-m,m),即可判断顶点所在直线.
5.
x<-1或x>3
【分析】由抛物线与x轴的一个交点(3,0)和对称轴x=1可以确定另一交点坐标为(-1,0),又y=ax2+bx+c>0时,图象在x轴上方,由此可求x的取值范围.
6.
m≥-2
【分析】根据二次函数性质,利用二次函数的对称轴不大于2列式计算即可得解.
7.
6
【解答】∵抛物线y=ax2+3与y轴交于点A,∴A点坐标为(0,3).
当y=3时,
x2=3,解得x=±3,∴B点坐标为(-3,3),C点坐标为(3,3),
∴BC=3-(-3)=6.
8.(1)∵函数y=x2-4x+m-1,抛物线与x轴只有一个交点,
∴b2-4ac=16-4(m-1)=20-4m=0,解得:m=5.
(2)联立抛物线与直线解析式消掉y得,x2-4x+m-1=2x-m,整理得,x2-6x+2m-1=0,
∵抛物线与直线只有一个交点,∴△=b2-4ac=(-6)2-4×1×(2m-1)=0,解得m=5.
9.(1)由抛物线过(0,-3),得:-3=|a|-4,∴|a|=1,即a=±1.
∵抛物线开口向上,∴a=1,∴抛物线的解析式为y=x2-2x-3.
(2)∵y=x2-2x-3=(x-1)2-4,∴当x=1时,y有最小值-4.
10.(1)∵=,设BD=x,∴DE=x,
设△ADE中DE边上的高为h,∵DE∥AC,∴h=CD=BC-BD=8-x,
∴y=DE?CD=×x?(8-x),即y=﹣x2+3x.
自变量x的取值范围是0<x<8.
(2)x=﹣
EQ
\F(3,2×(﹣))=4时,y最大==6,即当x=4时,△ADE的面积最大为6.
B组
1.
D
【解答】二次函数y=ax2+c的对称轴是y轴,当x取x1,x2(x1≠x2)时,函数值相等,即以x1,x2为横坐标的点关于y轴对称,则x1+x2=0,此时函数值为y=ax2+c=0+c=c.
2.
C
【解答】∵对称轴是x=,0<x1<,故由对称性<x2<1,
当x=a时,y<0,则a的范围是x1<a<x2,∴a-1<0,当x<时y随x的增大而减小,
当x=0时函数值是m.因而当x=a-1<0时,函数值y一定大于m.
3.
D
【解答】①∵抛物线y2=(x-3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=,故本小题错误;
③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=(x+2)2-3,
当x=0时,y1=(0+2)2-3=﹣,y2=(0-3)2+1=,故y2-y1=+=,故本小题错误;
④∵物线y1=a(x+2)2-3与y2=(x-3)2+1交于点A(1,3),
∴y1的对称轴为x=-2,y2的对称轴为x=3,∴B(-5,3),C(5,3)
∴AB=6,AC=4,∴2AB=3AC,故本小题正确.
4.
C
【解答】抛物线y=-4x+x2-7可化为y=(x-2)2-11的形式,
①因为抛物线y=-4x+x2-7中,a=1>0,所以抛物线开口向上,故本小题正确;
②由抛物线顶点式可知,其对称轴方程是x=2,故本小题正确;
③由抛物线顶点式可知,其顶点坐标是(2,-11),故本小题错误;
④当x=﹣时,y=(﹣-2)2-11=﹣,故本小题错误.
⑤因为△=(-4)2-4×1×(-7)=44>0,所以抛物线与x轴有两个不同的交点,故正确.
5.﹣2
【解答】设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=﹣,则ac=﹣?2m=-2.
6.
(4,5)或(-2,5)
【解答】由x2-2x-3=0得x1=3,x2=-1,∴AB距离为4,
要使△ABC的面积为10,C的纵坐标应为5,
把y=5时代入函数y=x2-2x-3得x2-2x-3=5,解得x1=4,x2=-2.
∴C点坐标为(4,5)或(-2,5).
7.
-1或2或0
【解答】∵抛物线y=(m-1)x2+2x+m图象与坐标轴有且只有2个交点,
而抛物线与y轴始终有一个交点,∴与x轴只有一个交点,
∴△=4-2(m-1)m=0,∴m=-1或2;
另外当m=0时,y=-x2+2x与x轴的一个交点(0,0)正好是与y轴的交点,即此时也与坐标轴只有两个交点.
综上,m=-1或2或0.
8.y=﹣(x+7)(x-1)
【解答】∵该函数图象与x轴两交点间的距离是8,对称轴为x=-3,
∴抛物线与x轴的两个交点坐标是(-7,0)、(1,0).
故设该抛物线解析式为y=a(x+7)(x-1)(a≠0).
把顶点(-3,4)代入得到:4=a(-3+7)(-3-1),解得a=﹣.
则该二次函数解析式为:y=﹣(x+7)(x-1).
9.24<a<36
【解答】抛物线的对称轴为直线x=﹣=,
∵在x=6或x=7时取得最小值,x是整数,
∴
>5.5①
<7.5②,
解不等式①得,a>24,解不等式②得,a<36,
∴不等式组的解是24<a<36,即a的取值范围是24<a<36.
10.(1)把(-2,5)代入二次函数y=x2+bx-3得:5=4-2b-3,∴b=-2,
∴y=x2-2x-3=(x-1)2-4,∴抛物线的开口方向向上,对称轴是直线x=1,
把x=1代入得y=-4,x=3代入得y=0,∴当1<x≤3时y取值范围是-4<y≤0.
(2)①当m=4时,y1、y2、y3不能作为同一个三角形三边的长.
理由是当m=4时,P1(4,y1)、P2(5,y2)、P3(6,y3),
代入抛物线的解析式得:y1=5,y2=12,y3=21,
∵5+12<21,∴当m=4时,y1、y2、y3不能作为同一个三角形三边的长.
②理由是:∵把P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)代入y=x2-2x-3=(x-1)2-4得:∴y1=(m-1)2-4,y2=(m+1-1)2-4,y3=(m+2-1)2-4,
∴y1+y2-y3=(m-1)2-4+(m+1-1)2-4-[(m+2-1)2-4]=(m-2)2-8,
∵m≥5,∴(m-2)2-8>0,∴y1+y2>y3,
根据三角形的三边关系定理:三角形的任意两边之和大于第三边(也可求出两小边的和大于第三边),
∴当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长.
五、优化提高
1.
B
【解答】根据定义可得函数y=2mx2+(1-m)x+(-1-m),
①当m=-3时,函数解析式为y=-6x2+4x+2,
∴﹣=﹣=,
==,∴顶点坐标是(,),正确.
②函数y=2mx2+(1-m)x+(-1-m)与x轴两交点坐标为(1,0),(﹣,0),
当m>0时,1-(﹣)=+>,正确;
③当m<0时,函数y=2mx2+(1-m)x+(-1-m)开口向下,对称轴x=->,
∴x可能在对称轴左侧也可能在对称轴右侧,错误;
④y=2mx2+(1-m)x+(-1-m)=m(2x2-x-1)+x-1,若使函数图象恒经过一点,m≠0时,应使2x2-x-1=0,可得x1=1,x2=﹣,当x=1时,y=0,当x=﹣时,y=﹣,则函数一定经过点(1,0)和(﹣,﹣),正确.
2.
x?1
【解答】由已知得抛物线顶点坐标为(2a,a-1),
设x=2a①,y=a-1②,
①-②×2,消去a得,x-2y=2,即y=x-1.
3.(1)根据题意,当x=0时,y=5;当x=1时,y=2;
∴
5=c
2=1+b+c
解得b=?4,c=5,∴该二次函数关系式为y=x2-4x+5.
(2)∵y=x2-4x+5=(x-2)2+1,
∴当x=2时,y有最小值,最小值是1.
(3)∵A(m,y1),B(m+1,y2)两点都在函数y=x2-4x+5的图象上,
∴y1=m2-4m+5,y2=(m+1)2-4(m+1)+5=m2-2m+2,
y2-y1=(m2-2m+2)-(m2-4m+5)=2m-3,
∴①当2m-3<0,即m<时,y1>y2;
②当2m-3=0,即m=时,y1=y2;
③当2m-3>0,即m>时,y1<y2.
4.
(1)当对称轴是x=-2,
∴x=﹣==-2,解得:a=-1.
(2)①当a=0时,方程为一元一次方程,方程ax2-(1-3a)x+2a-1=0有一个实数根.
②∵当a≠0时,方程为一元二次方程,
∴△=[-(1-3a)]2-4a(2a-1)=a2-2a+1=(a-1)2≥0,
∴方程有实数根,
∴a取任何实数时,方程ax2-(1-3a)x+2a-1=0总有实数根.
5.(1)∵抛物线与y轴交于点(0,3a),∴c=3a,
∵对称轴为=1,∴x=﹣=1,∴b=-2a.
(2)∵抛物线与直线y=x-1交于点(2,1),
∴(2,1)在抛物线上,
∴1=a×22+2(-2a)+3a,∴a=,
∴b=﹣2a=﹣,c=3a=1,
∴抛物线为y=x2-x+1.
(3)∵b(c+6)=﹣2a(3a+6)=﹣6a2-12a=﹣6(a+1)2+6,
当a=﹣1时,b(c+6)的最大值为6;
∴抛物线y=﹣x2+2x-3=﹣(x-1)2-2,故抛物线的顶点坐标为(1,-2).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
