浙教版九年级上册数学 第4讲 二次函数与系数、方程、不等式同步学案(含答案)
文档属性
| 名称 | 浙教版九年级上册数学 第4讲 二次函数与系数、方程、不等式同步学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 11:43:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4讲
二次方程与系数、方程、不等式
一、课前检测
1.
二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
(第1题图)
(第2题图)
2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;
③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确
的个数为( )
A.1
B.2
C.3
D.4
3.
已知拋物线y=﹣x2+2,当1≤x≤5时,y的最大值是( )
A.2
B.
C.
D.
4.
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
5.
已知函数表达式为y=x2-4x+3.
(1)该函数的图象与x轴有几个交点?并求出交点坐标;
(2)画出函数y=x2-4x+3的图象,观察图象直接写出当y>0时或y<0时相应的x的
取值范围.
(3)试问:当x为何值时,函数值y为15.
二、考点梳理
考点一、二次函数的图象、性质与系数的关系
1.
a的正负决定抛物线的开口方向:
a>0,开口向上
a<0,开口向下
2.
a与b决定抛物线的对称轴x=﹣的位置:
a,b同号,对称轴在y轴左侧
a,b异号,对称轴在y轴右侧
3.
c决定抛物线与y轴交点的位置:
c>0,交点在y轴的正半轴上
c=0,交点是原点
c<0,交点在y轴的负半轴上
4.
b2-4ac决定抛物线与x轴有无交点
b2-4ac>0,有两个交点
b2-4ac=0,只有一个交点
b2-4ac<0,没有交点
5.
a+b+c与a-b+c是由点(1,a+b+c)与点(-1,a-b+c)确定的.同理,也可确
定4a+2b+c,4a-2b+c,9a+3b+c,9a-3b+c等代数式的符号.
考点二、二次函数与一元二次不等式的关系
1.
不等式ax2+bx+c>0(a≠0)的解为y=ax2+bx+c(a≠0)
在x轴上方的点所对应的x值所组成的范围.
2.
不等式ax2+bx+c<0(a≠0)的解为y=ax2+bx+c(a≠0)
在x轴下方的点所对应的x值所组成的范围.
3.
不等式中如果带有等号,其解集也相应带有等号.
考点三、二次函数与一元二次方程之间的关系
1.
已知二次函数y=ax2+bx+c的函数值为k,求自变量x的值,就是一元二次方程ax2+
bx+c=k,反过来,解一元二次方程ax2+bx+c=k,就是把二次函数y=ax2+bx+c-
k的函数值看做0,求自变量的值.学习理解这部分知识,可以类比一次函数与一元一次
方程的关系.
2.
抛物线与x轴的交点与一元二次方程根的关系:
若抛物线与x轴没有交点一元二次方程没有实数根b2-4ac<0;
若抛物线与x轴有一个交点一元二次方程有两个相等的实数根b2-4ac=0;
若抛物线与x轴有两个交点一元二次方程有两个不相等实数根b2-4ac>0.
3.
抛物线y=ax2+bx+c与x轴的两个交点(x1,0)(x2,0),同样满足x1+x2=﹣,
x1·x2=,两个交点之间的距离|x1-x2|=.
三、重点突破
例1.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:
①abc<0;②2a+b=0;③a-b+c>0;④4a+c<2b;⑤4ac-b2<0.其中正确的是( )
A.①②⑤
B.只有①
C.③④
D.①④⑤
(点拨:注意数形结合)
(例1图)
(例2图)
例2.
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,
n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )
A.m<n
B.m>n
C.m=n
D.m、n的大小关系不能确定
(点拨:先判断a,b,c的符号)
例3.
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2
-4ac.则
M,N,P,Q中,值小于0的数有________个.
(点拨:利用对称轴的范围求2a与b的关系)
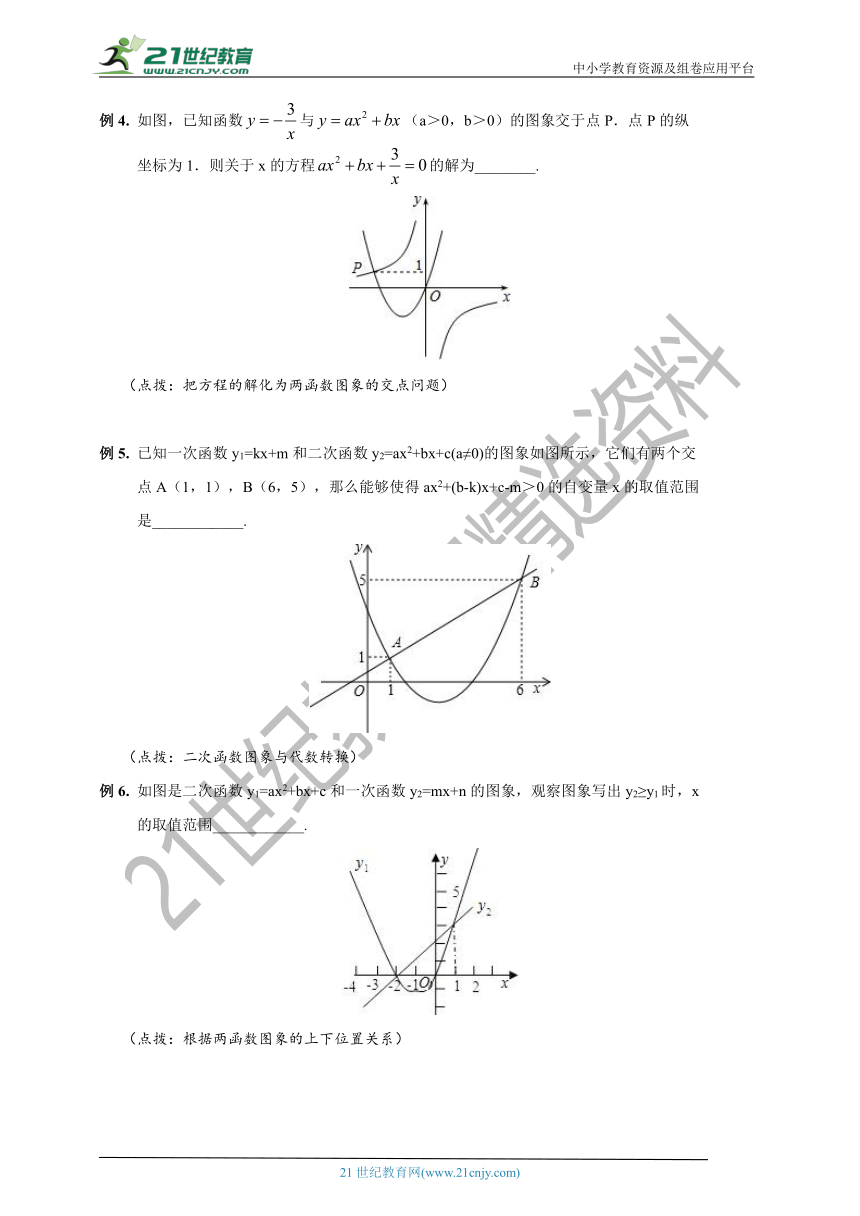
例4.
如图,已知函数与(a>0,b>0)的图象交于点P.点P的纵
坐标为1.则关于x的方程的解为________.
(点拨:把方程的解化为两函数图象的交点问题)
例5.
已知一次函数y1=kx+m和二次函数y2=ax2+bx+c(a≠0)的图象如图所示,它们有两个交
点A(1,1),B(6,5),那么能够使得ax2+(b-k)x+c-m>0的自变量x的取值范围
是____________.
(点拨:二次函数图象与代数转换)
例6.
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x
的取值范围____________.
(点拨:根据两函数图象的上下位置关系)
例7.(1)请在坐标系中画出二次函数y=x2-2x的大致图象.
(2)根据方程的根与函数图象的关系,将方程x2-2x=1的根在图上近似的表示出来
(描点).
(3)观察图象,直接写出方程x2-2x=1的根.(精确到0.1)
(点拨:(1)确定顶点坐标和与x轴y轴交点,作出图形)
例8.如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的
立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立
柱FE的高度为3.6米.
(1)求正中间的立柱OC的高度;
(2)是否存在一根立柱,其高度恰好是OC的一半?请说明理由.
(点拨:以O为原点,以AB所在的直线为x轴,建立直角坐标系)
例9.已知A=a+2,B=a2-a+5,C=a2+5a-19,其中a>2.
(1)比较A,B的大小.
(2)比较A,C的大小.
(点拨:作差法比较大小)
例10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k取值范围.
四、经典练习
A组
(一)选择题(共5小题)
1.
如图,将二次函数y=31x2
-999x+892的图形画在坐标
平面上,判断方程31x2
-999x+892=0的两根,下列叙
述何者正确( )
A.两根相异,且均为正根
B.两根相异,且只有一个正根
C.两根相同,且为正根
D.两根相同,且为负根
2.
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(第2题图)
(第3题图)
3.
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,
设P=a+b+c,则P的取值范围是( )
A.-3<P<-1
B.-6<P<0
C.-3<P<0
D.-6<P<-3
4.
如图,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式﹣+x2
+1<0的解集是( )
A.x>1
B.x<-1
C.-1<x<0
D.0<x<1
(第4题图)
(第5题图)
5.
菱形ABCD边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD
上一动点,AE+CF=4,则△BEF面积的最小值为( )
A.2
B.3
C.4
D.6
(二)
填空题(共2小题)
6.
若实数a,b满足a+b2=1,则2a2+7b2的最小值是_________.
7.
若抛物线y=x2-bx+9的顶点在x轴上,则b的值为_________.
(三)解答题(共3小题)
8.
一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是
,铅球运行路线如图.
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
9.
利用图象判断方程x2=3x-2是否有解,若有解,请写出它的近似解(结果精确到0.1).
10.
已知一元二次方程x2+px+q+1=0的一根为2.
(1)求q关于p的关系式;
(2)若p=2q,求方程的另一根;
(3)求证:抛物线y=x2+px+q与x轴有两个交点.
B组
(一)选择题(共5小题)
1.
方程2x-x2=的正根的个数为( )
A.0个
B.1个
C.2个
D.3个
2.
二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx-t=0
(t为实数)在-1<x<4的范围内有解,则t的取值范围是( )
A.t≥-1
B.-1≤t<3
C.-1≤t<8
D.3<t<8
3.
某幢建筑物,从10m高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在
平面与墙面垂直).如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落
地点B离墙的距离OB是( )
A.2
m
B.3
m
C.4
m
D.5
m
4.
关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:
①2a+b<0;②ab<0;③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;④抛物线
y=2x2+ax+b-2的顶点在第四象限.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2
+bx+c|=k(k≠0)有两个不相等
的实数根,则k的取值范围是( )
A.k<-3
B.k>-3
C.k<3
D.k>3
(二)填空题(共2小题)
6.
如图,已知抛物线y=x2+bx+c经过点(0,-3),请你确定一个b的值,使该抛物线与x
轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是___________.
7.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s
的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不
与点C重合).如果P、Q分别从A、B同时出发,那么经过_______秒,四边形APQC的
面积最小.
(三)解答题(共3小题)
8.
(?http:?/??/?www.m?/?math?/?report?/?detail?/?b3e75d2e-66d9-4bbd-a32c-0b021841e315"
\t
"http:?/??/?www.m?/?math?/?ques?/?detail?/?_blank?)如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴
交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,
请说明理由.
9.
如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,-4),B(x1,0),
C(x2,0)三点,且|x2-x1|=5.
(1)求b,c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,
求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
10.
已知抛物线y=ax2+bx+c与y轴交于点C,与x轴交于点A(x1,0)、B(x2,0)(x1
<x2),顶点M的纵坐标为-4,若x1、x2是方程x2-2(m-1)x+m2-7=0的两个根,且x21+x22=10.
(1)求A、B两点的坐标;
(2)求抛物线的解析式及点C的坐标;
(3)在抛物线上是否存在点P,使三角形PAB的面积等于四边形ACMB的面积的2倍?若
存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
五、优化提高
1.
已知二次函数y=ax2+bx+c的图象与x轴交于(1,0)和(x1,0),其中
-2
<x1<-1,与y轴交于正半轴上一点.下列结论:①b>0;②ac<b2;
③a>b;④-a<c<-2a.其中所有正确结论的序号是____________.
2.
求y=-x2+2x-2在t≤x≤t+1上的最大值和最小值.(t为常数)
3.
若、是关于一元二次方程(a≠0)的两个根,则方程的两个根、
和系数a、b、c有如下关系:,.把它称为一元二次方程根与系
数关系定理.如果设二次函数(a≠0)的图象与x轴的两个交点为A(,
0),B(,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:
.
参考以上定理和结论,解答下列问题:
设二次函数(a>0)的图象与x轴的两个交点A(,0),B(,0),
抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求的值;
(2)当△ABC为等边三角形时,求的值.
4.
(?http:?/??/?www.m?/?math?/?report?/?detail?/?12af6e7d-d15b-4531-b9aa-290d3c2ca33e"
\t
"http:?/??/?www.m?/?math?/?ques?/?detail?/?_blank?)已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标
为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点
的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的
对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,
使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;
若不存在,请说明理由.
参考答案
一、课前检测
1.
B
【分析】根据二次函数的图象判断得出a>0,﹣>0,∴b<0,再判断一次函数图象与实际是否相符,判断正误.
2.
C
【解答】根据图示知,抛物线开口方向向上,抛物线与y轴交与负半轴,对称轴在y轴右侧,则a>0,c<0,b<0,所以abc>0.故①错误;
根据图象得对称轴x=1,即﹣=1,所以b=-2a,即2a+b=0,故②正确;
当x=3时,y=0,即9a+3b+c=0.故③错误;
根据图示知,当-1<x<3时,y<,故④正确;
根据图示知,当x<0时,y随x的增大而减小,故⑤正确.
3.
C
4.
D
【解答】∵二次函数y=kx2-6x+3的图象与x轴有交点,
∴方程kx2-6x+3=0(k≠0)有实数根,
即△=36-12k≥0,k≤3,由于是二次函数,故k≠0,则k的取值范围是k≤3且k≠0.
5.解方程x2-4x+3=0,得x1=1,x2=3,所以该函数的图象与x轴有两个交点,交点坐标分别为(1,0),(3,0).
(2)y=x2
-4x+3=(x-2)2-1,画图略.
当x<1或x>3时,y>0;当1<x<3时,y<0.
(3)令x2-4x+3=15,得x2-4x-12=0,解得x1=-2,x2=6.
故当x=-2或x=6时,函数y=x2-4x+3的值为15.
三、重点突破
例1.
D
【分析】根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号.
例2.
A
【解答】∵抛物线开口向下,∴a<0,
∵对称轴在y轴右边,∴b>0,
∵抛物线经过原点,∴c=0,
∴a-b+c<0;
∵x=1时,y>0,∴a+b+c>0,
∵c=0,∴a+b>0.
∵x=﹣>1,a<0,∴b>-2a,∴2a+b>0,
m=|a-b+c|+|2a+b+c|=b-a+(2a+b)=a+2b,
n=|a+b+c|+|2a-b-c|=a+b+(b-2a)=2b-a,
∵m-n=(a+2b)-(2b-a)=2a,
∵a<0,∴2a<0,即m-n<0,∴m<n.
例3.
3
【解答】∵图象开口向下,∴a<0,
∵对称轴在y轴左侧,∴a,b同号,∴a<0,b<0,
∵图象经过y轴正半轴,∴c>0,
∴M=a+b-c<0;
当x=-2时,y=4a-2b+c<0,∴N=4a-2b+c<0;
∵﹣>-1,a<0,∴b>2a,∴2a-b<0,
∴P=2a-b<0;
∵图象与x轴有两个交点,∴b2-4ac>0,Q=b2-4ac>0.
值小于0的数有M,N,P共3个.
例4.
x=-3
【解答】∵P的纵坐标为1,∴1=﹣,∴x=-3,
∵ax2+bx+=0化为于x的方程ax2+bx=﹣的形式,
∴此方程的解即为两函数图象交点的横坐标的值,∴x=-3.
例5.
x<1或x>6
【分析】求ax2+(b-k)x+c-m>0自变量的取值范围也就是求ax2+bx+c>kx+m,即y2>y1的自变量取值范围,从图上看就是二次函数图象在上方一次函数图象时,横坐标x的取值范围.
例6.
-2≤x≤1
例7.(1)如下图,y=x2
-2x=(x-1)2-1,
作出顶点,作出与x轴的交点,图象光滑.
(2)正确作出点M,N;
(3)写出方程的根为-0.4,2.4.
例8.(1)根据题意可得中间立柱OC经过AB的中点O.
如图,以点O为原点,以AB所在的直线为x轴,建立直角坐标系.
问题转化为求点C的纵坐标.
|OF|=40(米),故B(50,0),E(-40,3.6)
设抛物线的解析式为y=ax2+c
∴
502a+c=0
402a+c=3.6
解得:a=﹣,c=10,
(2)设存在一根立柱的高度是OC的一半,即这根立柱的高度是5米.
则有﹣x2+10=5.解得:x=±25,
∵相邻立柱之间的间距为10米.最中间的立柱OC在y轴上,
根据题意每根立柱上的点的横坐标为10的整数倍,
∴x=±25与题意不符,∴不存在一根立柱,其高度恰好是OC高度的一半.
例9.(1)B-A=(a-1)2+2>0,∴B>A.
(2)C-A=a2+5a-19-a-2
=a2+4a-21
=(a+7)(a-3).
∵a>2,∴a+7>0,
从而当2<a<3时,A>C;
当a=3时,A=C;当a>3时,A<C.
例10.(1)由图象可知,图象与x轴交于(1,0)和(3,0)点,则方程ax2+bx+c=0的两个根为1和3.
(2)由图象可知当1<x<3时,不等式ax2+bx+c>0.
(3)由图象可知,y=ax2+bx+c(a≠0)的图象的对称轴为x=2,开口向下,即当x>2时,y随x的增大而减小.
(4)由图象可知,二次函数y=ax2+bx+c(a≠0)的最大值为2,
若方程ax2+bx+c=k有两个不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,
则k<2.
四、经典练习
A组
1.
A
2.
C
【解答】∵抛物线开口向下,∴a<0,
∵抛物线与y轴的交于正半轴,∴c>0,
∵抛物线的对称轴在y轴的左侧,那么有当a与b同号时(即ab>0),对称轴在y轴左,
∴ab>0,即b<0,∴bc<0,∴点P(a,bc)在第三象限,
3.
B
【解答】∵抛物线y=ax2+bx+c(c≠0)过点(-1,0)和点(0,-3),
∴0=a-b+c,-3=c,∴b=a-3,
∵当x=1时,y=ax2+bx+c=a+b+c,∴P=a+b+c=a+a-3-3=2a-6,
∵顶点在第四象限,a>0,∴b=a-3<0,∴a<3,
∴0<a<3,∴-6<2a-6<0,即-6<P<0.
4.
D
【分析】先把不等式整理成x2+1<,然后根据图形找出二次函数图象在反比例函数图象下方部分的x的取值范围即可.
5.
B
【解答】连接BD,AC,
∵菱形ABCD边长为4,∠BAD=60°;∴△ABD与△BCD为正三角形;∴BD=4,AC=4,
△ABE的边AE上的高与△BCF的边CF上的高都为2,∠ADC=120°;
设AE为x,则CF为4-x;
∴S△DEF=ED?DFsin120°=(4-x)[4-(4-x)]
EQ
\F(,2)=﹣
EQ
\F(,4)x2+x,
由图示可知:S△BEF=S菱形ABCD-S△ABE-S△BCF-S△DEF
=×4×4-CF-AE-S△DEF
=8-(CF+AE)-S△DEF=8-4-S△DEF=
EQ
\F(,4)x2-x+4,
根据二次函数的性质,△BEF面积的最小值=﹣
=
EQ
\F(4×
EQ
\F(,4)×4-3,)=3.
6.
2
【解答】方法一:∵a+b2=1,∴a=1-b2,
∴2a2+7b2=2(1-b2)2+7b2
=2b4+3b2+2=2(b2+)2+2-=2(b2+)2+
,
∵b2≥0,∴2(b2+)2
+>0,
∴当b2=0,即b=0时,2a2+7b2的值最小.∴最小值是2.
方法二:∵a+b2=1,∴b2=1-a,
∴2a2+7b2=2a2+7(1-a)=2a2-7a+7=2(a-)2
+,
∵b2≥0,∴1-a≥0,∴a≤1,∴当a=1,即b=0时,2a2+7b2的值最小.∴最小值是2.
7.
±6
【分析】抛物线y=ax2+bx+c的顶点坐标为(﹣,),因为抛物线y=x2-bx+9的顶点在x轴上,所以顶点的纵坐标为零,列方程求解.
8.(1)当y=0时,﹣x2+x+=0,
解之得x1=10,x2=-2(不合题意,舍去),
∴推铅球的水平距离是10米.
(2)y=﹣x2+x+
=﹣(x2-8x+16-16)+
=﹣(x2-8x+16)++
=﹣(x-4)2+3,
当x=4时,y取最大值3,
∴铅球行进高度不能达到4m,最高能达到3m.
9.令y=x2-3x+2,画出其图象如图:
x1=3-≈1.7,x2=3+≈5.3.
10.(1)∵一元二次方程x2+px+q+1=0的一根为2,
∴4+2p+q+1=0,即q=-2p-5.
(2)设一元二次方程x2+px+q+1=0的一根为t,
则由韦达定理,得
2+t=?p
2t=q+1
p=2q
解得,t=0
,p=?2
,q=?1
,
∴原方程的另一根为0.
(3)证明:令x2+px+q=0.则△=p2-4q=p2-4(-2p-5)=(p+4)2+4>0,即△>0,
∴关于x的方程x2+px+q=0有两个不相等的实数根.即抛物线y=x2+px+q与x轴有两个交点.
B组
1.
A
【分析】此题实质是求函数y1=2x-x2和函数y2=的图象在一、四象限有没有交点,根据两个已知函数的图象的交点情况,直接判断.
【解答】设函数y1=2x-x2,函数y2=,
∵函数y1=2x-x2的图象在一、三、四象限,开口向下,顶点坐标为(1,1),对称轴x=1;
函数y2=的图象在一、三象限;而两函数在第一象限没有交点,交点在第三象限.
即方程2x-x2=的正根的个数为0个.
2.
C
【解答】对称轴为直线x=﹣=1,解得b=-2,
∴二次函数解析式为y=x2-2x,即y=(x-1)2-1,
x=-1时,y=1+2=3,
x=4时,y=16-2×4=8,
∵x2+bx-t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当-1≤t<8时,在-1<x<4的范围内有解.
3.
B
【解答】以抛物线所在平面与墙面的交线为y轴,和水平面的交线为x轴建立坐标系.
则由题设条件知,抛物线的顶点M(1,),
A点坐标为(0,10).
于是可设抛物线方程为y=a(x-1)2+.
将A点坐标(0,10)代入该方程可求得a的值为﹣.
∴抛物线方程为:y=﹣(x-1)2+.
令y=0,得(x-1)2=4,∴x=3或-1(舍去).∴B点的坐标为(3,0),故OB=3
m.
4.
C
【解答】∵x=2是方程2x2+ax+b=0的根,∴2×4+2a+b=0,∴2a+b=-8<0,故①正确;
∵x=2是方程2x2+ax+b=0的两个根中较小的根,∴﹣>2+2,>2×2,
∴a<-8,b>8,∴ab<0,故②正确;
∵方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,
∴二次函数y=2x2+ax+b与x轴有两个交点,且对称轴在直线x=2的右边,
∴二次函数y=2x2+ax+b顶点坐标在第四象限,
向上平移2个单位得到二次函数y=2x2+ax+b+2,与x轴不一定有交点,
∴关于x的方程2x2+ax+b+2=0有两个不相等的实数根错误,故③错误;
向下平移2个单位得到二次函数y=2x2+ax+b-2,顶点坐标一定在第四象限,故④正确;
综上所述,正确的结论有①②④共3个.
5.
D
【解答】∵当ax2+bx+c≥0,y=ax2+bx+c(a≠0)的图象在x轴上方,
∴此时y=|ax2+bx+c|=ax2+bx+c,
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象,
∵当ax2+bx+c<0时,y=ax2+bx+c(a≠0)的图象在x轴下方,
∴此时y=|ax2+bx+c|=-(ax2+bx+c)
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象,
∵y=ax2+bx+c(a≠0)的顶点纵坐标是-3,
∴函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象的顶点纵坐标是3,
∴y=|ax2+bx+c|的图象如图,
∵观察图象可得当k≠0时,
函数图象在直线y=3的上方时,纵坐标相同的点有两个,
函数图象在直线y=3上时,纵坐标相同的点有三个,
函数图象在直线y=3的下方时,纵坐标相同的点有四个,
∴若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,
则函数图象应该在y=3的上边,故k>3.
6.1(在-2<b<2范围内的任何一个数)
【解答】把(0,-3)代入抛物线的解析式得:c=-3,∴y=x2+bx-3,
∵使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,
∴把x=1代入y=x2+bx-3得:y=1+b-3<0
把x=3代入y=x2+bx-3得:y=9+3b-3>0,
∴-2<b<2,
即在-2<b<2范围内的任何一个数都符合.
7.
3
【解答】设P、Q同时出发后经过的时间为t
s,四边形APQC的面积为S
mm2,
则有:S=S△ABC-S△PBQ=×12×24-×4t×(12?2t)
=4t2-24t+144
=4(t-3)2+108.
∵4>0∴当t=3s时,S取得最小值.
8.(1)依题意:x1+x2=-m,x1x2=m-1,
∵x12+x22+x1x2=7,∴(x1+x2)2-x1x2=7,
∴(-m)2-(m-1)=7,即m2-m-6=0,解得m1=-2,m2=3,
∵c=m-1<0,∴m=3不合题意,∴m=-2,∴抛物线的解析式是y=x2-2x-3.
(2)能.理由如下:
如图,设P是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
若∠POC=∠PCO,则PD应是线段OC的垂直平分线,
∵C的坐标为(0,-3),∴D的坐标为(0,-),
∴P的纵坐标应是-
,
令x2-2x-3=-,解得,x1=
EQ
\F(2?,2),x2=
EQ
\F(2+,2),
∴所求点P的坐标是(
EQ
\F(2?,2),-),(
EQ
\F(2+,2),-).
9.(1)∵抛物线y=﹣x2+bx+c,经过点A(0,-4),∴c=-4,
又∵由题意可知,x1、x2是方程﹣x2+bx+c的两个根,∴x1+x2=b,x1x2=6,
由已知得(x2-x1)2=25,
又∵(x2-x1)2=(x2+x1)2-4x1x2=b2-24,∴b2-24=25,解得b=±,
当b=时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.∴b=﹣.
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,
又∵y=﹣x2﹣x﹣4=﹣(x+)2+,
∴抛物线的顶点(-,)即为所求的点D.
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),根据菱形的性质,点P必是直线x=-3与抛物线y=﹣x2﹣x﹣4
的交点,
∴当x=-3时,y=﹣×(-3)2﹣×(-3)﹣4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形.
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上.
10.(1)∵x1,x2是方程x2-2(m-1)x+m2-7=0的两个根,
∴x1+x2=2(m-1),x1?x2=m2-7.
又∵x12+x22=10,∴(x1+x2)2-2x1x2=10,
∴[2(m-1)]2-2(m2-7)=10,即m2-4m+4=0.解得:m1=m2=2.
将m=2代入方程x2-2(m-1)x+m2-7=0,得:x2-2x-3=0,解得:x1=-1,x2=3.
∴点A的坐标为(-1,0),点B的坐标为(3,0).
(2)因为抛物线与x轴的交点为A(-1,0)、B(3,0),由对称性可知,顶点M的横坐标为1,则顶点M的坐标为(1,-4).
∴
a?b+c=0
9a+3b+c=0
a+b+c=?4
解得:a=1,b=?2,c=?3,
∴抛物线的解析式为y=x2-2x-3.
在y=x2-2x-3中,令x=0,得y=-3.∴点C的坐标为(0,-3).
(3)设抛物线的对称轴与x轴交于点D,
则AO=OD=1,DB=2,OC=3,
DM=4,AB=4.
∴S四边形ACMB=S△ACO+S梯形OCMD+S△DMB
=?AO?CO+(CO+MD)+DB?MD
=×1×3+×(3+4)×1+×2×4=9.
设P(x0,y0)为抛物线上一点,
则S△PAB=AB?|y0|.
若S△PAB=2S四边形ACMB,则?AB?|y0|=18,
∴丨y0丨=9,y0=±9.
将y0=9代入y=x2-2x-3中,得x2-2x-3=9,即x2-2x-12=0,
解得:x1=1-,x2=1+.
将y0=-9代入y=x2-2x-3中,得:x2-2x-3=-9,
即x2-2x+6=0.
∵△=(-2)2-4×1×6=-20<0,
∴此方程无实数根.
∴符合条件的点P有两个:P1(1-,9),P2(1+,9).
五、优化提高
1.②④
【解答】∵抛物线与x轴的交点为(1,0)和(x1,0),-2<x1<-1,与y轴交于正半轴,
∴a<0,
∵-2<x1<-1,∴﹣<﹣<0,∴b<0,b>a,故①错误,③错误;
∵抛物线与x轴有两个交点,∴b2-4ac>0,∴ac<b2,故②正确;
∵抛物线与x轴的交点有一个为(1,0),∴a+b+c=0,∴b=-a-c,
∵b<0,b>a(已证),∴-a-c<0,-a-c>a,∴c>-a,c<-2a,
∴-a<c<-2a,故④正确,
综上所述,正确的结论有②④.
2.
∵二次函数y=-x2+2x-2=-(x-1)2-1,∴开口向下,对称轴为x=1,
当t+1<1,即t<0时,
函数y的最小值是-t2+2t-2,最大值为-(t+1)2+2(t+1)-2=-t2+1;
当t≤1≤t+1,即0≤t≤1时,
函数y的最小值是-t2+2t-2,最大值为-1;
当t>1时,
函数y的最大值是-t2+2t-2,最小值为-t2+1.
3.
当△ABC为直角三角形时,过C作CE⊥AB于E,则AB=2CE.
∵抛物线与x轴有两个交点,∴△=b2
-4ac>0,则|b2-4ac|=b2-4ac.
∵a>0,∴AB=
EQ
\F(,|a|)
=
EQ
\F(,a)
,
又∵CE=||=,
∴
EQ
\F(,a)
=2×,
∴=,
∴b2-4ac=,
∵b2-4ac>0,∴b2-4ac=4.
(2)当△ABC为等边三角形时,
由(1)可知CE=
EQ
\F(,2)AB,
∴=
EQ
\F(,2)×
EQ
\F(,a)
,
∵b2-4ac>0,∴=,∴b2-4ac=12.
4.(1)∵抛物线y=ax2+bx+8经过点A(-6,0),B(4,0),
∴
36a?6b+8=0
16a+4b+8=0
解得a=﹣,b=﹣,∴抛物线的解析式是:y=﹣x2﹣x+8.
(2)如图①,作DM⊥抛物线的对称轴于点M,设G坐标为(-1,n),
由翻折的性质,可得BD=DG,
∵B(4,0),C(0,8),点D为BC的中点,
∴点D的坐标是(2,4),
∴点M的坐标是(-1,4),DM=2-(-1)=3,
∵B(4,0),C(0,8),∴BC==4,∴BD=2,
在Rt△GDM中,32+(4-n)2=20,解得n=4±,
∴G点的坐标为(-1,4+)或(-1,4-).
(3)抛物线y=ax2+bx+8对称轴上存在F,使得以C、D、E、F为顶点的四边形为平行四边形.
①当CD∥EF,且点E在x轴的正半轴时,如图②,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得,c=1,d=4,∴点F的坐标是(-1,4),E坐标是(1,0).
②当CD∥EF,且点E在x轴的负半轴时,如图③
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得c=?3
,d=?4
,
∴点F的坐标是(-1,-4),点E的坐标是(-3,0).
③当CE∥DF时,如图④,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得c=3
,d=12
,
∴点F的坐标是(-1,12),点E的坐标是(3,0).
综上,可得抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,点F的坐标是(-1,4)、(-1,-4)或(-1,12).
简记“左同右异”
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第4讲
二次方程与系数、方程、不等式
一、课前检测
1.
二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
(第1题图)
(第2题图)
2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;
③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确
的个数为( )
A.1
B.2
C.3
D.4
3.
已知拋物线y=﹣x2+2,当1≤x≤5时,y的最大值是( )
A.2
B.
C.
D.
4.
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
5.
已知函数表达式为y=x2-4x+3.
(1)该函数的图象与x轴有几个交点?并求出交点坐标;
(2)画出函数y=x2-4x+3的图象,观察图象直接写出当y>0时或y<0时相应的x的
取值范围.
(3)试问:当x为何值时,函数值y为15.
二、考点梳理
考点一、二次函数的图象、性质与系数的关系
1.
a的正负决定抛物线的开口方向:
a>0,开口向上
a<0,开口向下
2.
a与b决定抛物线的对称轴x=﹣的位置:
a,b同号,对称轴在y轴左侧
a,b异号,对称轴在y轴右侧
3.
c决定抛物线与y轴交点的位置:
c>0,交点在y轴的正半轴上
c=0,交点是原点
c<0,交点在y轴的负半轴上
4.
b2-4ac决定抛物线与x轴有无交点
b2-4ac>0,有两个交点
b2-4ac=0,只有一个交点
b2-4ac<0,没有交点
5.
a+b+c与a-b+c是由点(1,a+b+c)与点(-1,a-b+c)确定的.同理,也可确
定4a+2b+c,4a-2b+c,9a+3b+c,9a-3b+c等代数式的符号.
考点二、二次函数与一元二次不等式的关系
1.
不等式ax2+bx+c>0(a≠0)的解为y=ax2+bx+c(a≠0)
在x轴上方的点所对应的x值所组成的范围.
2.
不等式ax2+bx+c<0(a≠0)的解为y=ax2+bx+c(a≠0)
在x轴下方的点所对应的x值所组成的范围.
3.
不等式中如果带有等号,其解集也相应带有等号.
考点三、二次函数与一元二次方程之间的关系
1.
已知二次函数y=ax2+bx+c的函数值为k,求自变量x的值,就是一元二次方程ax2+
bx+c=k,反过来,解一元二次方程ax2+bx+c=k,就是把二次函数y=ax2+bx+c-
k的函数值看做0,求自变量的值.学习理解这部分知识,可以类比一次函数与一元一次
方程的关系.
2.
抛物线与x轴的交点与一元二次方程根的关系:
若抛物线与x轴没有交点一元二次方程没有实数根b2-4ac<0;
若抛物线与x轴有一个交点一元二次方程有两个相等的实数根b2-4ac=0;
若抛物线与x轴有两个交点一元二次方程有两个不相等实数根b2-4ac>0.
3.
抛物线y=ax2+bx+c与x轴的两个交点(x1,0)(x2,0),同样满足x1+x2=﹣,
x1·x2=,两个交点之间的距离|x1-x2|=.
三、重点突破
例1.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:
①abc<0;②2a+b=0;③a-b+c>0;④4a+c<2b;⑤4ac-b2<0.其中正确的是( )
A.①②⑤
B.只有①
C.③④
D.①④⑤
(点拨:注意数形结合)
(例1图)
(例2图)
例2.
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,
n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )
A.m<n
B.m>n
C.m=n
D.m、n的大小关系不能确定
(点拨:先判断a,b,c的符号)
例3.
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2
-4ac.则
M,N,P,Q中,值小于0的数有________个.
(点拨:利用对称轴的范围求2a与b的关系)
例4.
如图,已知函数与(a>0,b>0)的图象交于点P.点P的纵
坐标为1.则关于x的方程的解为________.
(点拨:把方程的解化为两函数图象的交点问题)
例5.
已知一次函数y1=kx+m和二次函数y2=ax2+bx+c(a≠0)的图象如图所示,它们有两个交
点A(1,1),B(6,5),那么能够使得ax2+(b-k)x+c-m>0的自变量x的取值范围
是____________.
(点拨:二次函数图象与代数转换)
例6.
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x
的取值范围____________.
(点拨:根据两函数图象的上下位置关系)
例7.(1)请在坐标系中画出二次函数y=x2-2x的大致图象.
(2)根据方程的根与函数图象的关系,将方程x2-2x=1的根在图上近似的表示出来
(描点).
(3)观察图象,直接写出方程x2-2x=1的根.(精确到0.1)
(点拨:(1)确定顶点坐标和与x轴y轴交点,作出图形)
例8.如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的
立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立
柱FE的高度为3.6米.
(1)求正中间的立柱OC的高度;
(2)是否存在一根立柱,其高度恰好是OC的一半?请说明理由.
(点拨:以O为原点,以AB所在的直线为x轴,建立直角坐标系)
例9.已知A=a+2,B=a2-a+5,C=a2+5a-19,其中a>2.
(1)比较A,B的大小.
(2)比较A,C的大小.
(点拨:作差法比较大小)
例10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k取值范围.
四、经典练习
A组
(一)选择题(共5小题)
1.
如图,将二次函数y=31x2
-999x+892的图形画在坐标
平面上,判断方程31x2
-999x+892=0的两根,下列叙
述何者正确( )
A.两根相异,且均为正根
B.两根相异,且只有一个正根
C.两根相同,且为正根
D.两根相同,且为负根
2.
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(第2题图)
(第3题图)
3.
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,
设P=a+b+c,则P的取值范围是( )
A.-3<P<-1
B.-6<P<0
C.-3<P<0
D.-6<P<-3
4.
如图,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式﹣+x2
+1<0的解集是( )
A.x>1
B.x<-1
C.-1<x<0
D.0<x<1
(第4题图)
(第5题图)
5.
菱形ABCD边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD
上一动点,AE+CF=4,则△BEF面积的最小值为( )
A.2
B.3
C.4
D.6
(二)
填空题(共2小题)
6.
若实数a,b满足a+b2=1,则2a2+7b2的最小值是_________.
7.
若抛物线y=x2-bx+9的顶点在x轴上,则b的值为_________.
(三)解答题(共3小题)
8.
一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是
,铅球运行路线如图.
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
9.
利用图象判断方程x2=3x-2是否有解,若有解,请写出它的近似解(结果精确到0.1).
10.
已知一元二次方程x2+px+q+1=0的一根为2.
(1)求q关于p的关系式;
(2)若p=2q,求方程的另一根;
(3)求证:抛物线y=x2+px+q与x轴有两个交点.
B组
(一)选择题(共5小题)
1.
方程2x-x2=的正根的个数为( )
A.0个
B.1个
C.2个
D.3个
2.
二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx-t=0
(t为实数)在-1<x<4的范围内有解,则t的取值范围是( )
A.t≥-1
B.-1≤t<3
C.-1≤t<8
D.3<t<8
3.
某幢建筑物,从10m高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在
平面与墙面垂直).如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落
地点B离墙的距离OB是( )
A.2
m
B.3
m
C.4
m
D.5
m
4.
关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:
①2a+b<0;②ab<0;③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;④抛物线
y=2x2+ax+b-2的顶点在第四象限.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2
+bx+c|=k(k≠0)有两个不相等
的实数根,则k的取值范围是( )
A.k<-3
B.k>-3
C.k<3
D.k>3
(二)填空题(共2小题)
6.
如图,已知抛物线y=x2+bx+c经过点(0,-3),请你确定一个b的值,使该抛物线与x
轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是___________.
7.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s
的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不
与点C重合).如果P、Q分别从A、B同时出发,那么经过_______秒,四边形APQC的
面积最小.
(三)解答题(共3小题)
8.
(?http:?/??/?www.m?/?math?/?report?/?detail?/?b3e75d2e-66d9-4bbd-a32c-0b021841e315"
\t
"http:?/??/?www.m?/?math?/?ques?/?detail?/?_blank?)如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴
交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,
请说明理由.
9.
如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,经过A(0,-4),B(x1,0),
C(x2,0)三点,且|x2-x1|=5.
(1)求b,c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,
求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
10.
已知抛物线y=ax2+bx+c与y轴交于点C,与x轴交于点A(x1,0)、B(x2,0)(x1
<x2),顶点M的纵坐标为-4,若x1、x2是方程x2-2(m-1)x+m2-7=0的两个根,且x21+x22=10.
(1)求A、B两点的坐标;
(2)求抛物线的解析式及点C的坐标;
(3)在抛物线上是否存在点P,使三角形PAB的面积等于四边形ACMB的面积的2倍?若
存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
五、优化提高
1.
已知二次函数y=ax2+bx+c的图象与x轴交于(1,0)和(x1,0),其中
-2
<x1<-1,与y轴交于正半轴上一点.下列结论:①b>0;②ac<b2;
③a>b;④-a<c<-2a.其中所有正确结论的序号是____________.
2.
求y=-x2+2x-2在t≤x≤t+1上的最大值和最小值.(t为常数)
3.
若、是关于一元二次方程(a≠0)的两个根,则方程的两个根、
和系数a、b、c有如下关系:,.把它称为一元二次方程根与系
数关系定理.如果设二次函数(a≠0)的图象与x轴的两个交点为A(,
0),B(,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:
.
参考以上定理和结论,解答下列问题:
设二次函数(a>0)的图象与x轴的两个交点A(,0),B(,0),
抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求的值;
(2)当△ABC为等边三角形时,求的值.
4.
(?http:?/??/?www.m?/?math?/?report?/?detail?/?12af6e7d-d15b-4531-b9aa-290d3c2ca33e"
\t
"http:?/??/?www.m?/?math?/?ques?/?detail?/?_blank?)已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标
为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点
的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的
对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,
使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;
若不存在,请说明理由.
参考答案
一、课前检测
1.
B
【分析】根据二次函数的图象判断得出a>0,﹣>0,∴b<0,再判断一次函数图象与实际是否相符,判断正误.
2.
C
【解答】根据图示知,抛物线开口方向向上,抛物线与y轴交与负半轴,对称轴在y轴右侧,则a>0,c<0,b<0,所以abc>0.故①错误;
根据图象得对称轴x=1,即﹣=1,所以b=-2a,即2a+b=0,故②正确;
当x=3时,y=0,即9a+3b+c=0.故③错误;
根据图示知,当-1<x<3时,y<,故④正确;
根据图示知,当x<0时,y随x的增大而减小,故⑤正确.
3.
C
4.
D
【解答】∵二次函数y=kx2-6x+3的图象与x轴有交点,
∴方程kx2-6x+3=0(k≠0)有实数根,
即△=36-12k≥0,k≤3,由于是二次函数,故k≠0,则k的取值范围是k≤3且k≠0.
5.解方程x2-4x+3=0,得x1=1,x2=3,所以该函数的图象与x轴有两个交点,交点坐标分别为(1,0),(3,0).
(2)y=x2
-4x+3=(x-2)2-1,画图略.
当x<1或x>3时,y>0;当1<x<3时,y<0.
(3)令x2-4x+3=15,得x2-4x-12=0,解得x1=-2,x2=6.
故当x=-2或x=6时,函数y=x2-4x+3的值为15.
三、重点突破
例1.
D
【分析】根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号.
例2.
A
【解答】∵抛物线开口向下,∴a<0,
∵对称轴在y轴右边,∴b>0,
∵抛物线经过原点,∴c=0,
∴a-b+c<0;
∵x=1时,y>0,∴a+b+c>0,
∵c=0,∴a+b>0.
∵x=﹣>1,a<0,∴b>-2a,∴2a+b>0,
m=|a-b+c|+|2a+b+c|=b-a+(2a+b)=a+2b,
n=|a+b+c|+|2a-b-c|=a+b+(b-2a)=2b-a,
∵m-n=(a+2b)-(2b-a)=2a,
∵a<0,∴2a<0,即m-n<0,∴m<n.
例3.
3
【解答】∵图象开口向下,∴a<0,
∵对称轴在y轴左侧,∴a,b同号,∴a<0,b<0,
∵图象经过y轴正半轴,∴c>0,
∴M=a+b-c<0;
当x=-2时,y=4a-2b+c<0,∴N=4a-2b+c<0;
∵﹣>-1,a<0,∴b>2a,∴2a-b<0,
∴P=2a-b<0;
∵图象与x轴有两个交点,∴b2-4ac>0,Q=b2-4ac>0.
值小于0的数有M,N,P共3个.
例4.
x=-3
【解答】∵P的纵坐标为1,∴1=﹣,∴x=-3,
∵ax2+bx+=0化为于x的方程ax2+bx=﹣的形式,
∴此方程的解即为两函数图象交点的横坐标的值,∴x=-3.
例5.
x<1或x>6
【分析】求ax2+(b-k)x+c-m>0自变量的取值范围也就是求ax2+bx+c>kx+m,即y2>y1的自变量取值范围,从图上看就是二次函数图象在上方一次函数图象时,横坐标x的取值范围.
例6.
-2≤x≤1
例7.(1)如下图,y=x2
-2x=(x-1)2-1,
作出顶点,作出与x轴的交点,图象光滑.
(2)正确作出点M,N;
(3)写出方程的根为-0.4,2.4.
例8.(1)根据题意可得中间立柱OC经过AB的中点O.
如图,以点O为原点,以AB所在的直线为x轴,建立直角坐标系.
问题转化为求点C的纵坐标.
|OF|=40(米),故B(50,0),E(-40,3.6)
设抛物线的解析式为y=ax2+c
∴
502a+c=0
402a+c=3.6
解得:a=﹣,c=10,
(2)设存在一根立柱的高度是OC的一半,即这根立柱的高度是5米.
则有﹣x2+10=5.解得:x=±25,
∵相邻立柱之间的间距为10米.最中间的立柱OC在y轴上,
根据题意每根立柱上的点的横坐标为10的整数倍,
∴x=±25与题意不符,∴不存在一根立柱,其高度恰好是OC高度的一半.
例9.(1)B-A=(a-1)2+2>0,∴B>A.
(2)C-A=a2+5a-19-a-2
=a2+4a-21
=(a+7)(a-3).
∵a>2,∴a+7>0,
从而当2<a<3时,A>C;
当a=3时,A=C;当a>3时,A<C.
例10.(1)由图象可知,图象与x轴交于(1,0)和(3,0)点,则方程ax2+bx+c=0的两个根为1和3.
(2)由图象可知当1<x<3时,不等式ax2+bx+c>0.
(3)由图象可知,y=ax2+bx+c(a≠0)的图象的对称轴为x=2,开口向下,即当x>2时,y随x的增大而减小.
(4)由图象可知,二次函数y=ax2+bx+c(a≠0)的最大值为2,
若方程ax2+bx+c=k有两个不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,
则k<2.
四、经典练习
A组
1.
A
2.
C
【解答】∵抛物线开口向下,∴a<0,
∵抛物线与y轴的交于正半轴,∴c>0,
∵抛物线的对称轴在y轴的左侧,那么有当a与b同号时(即ab>0),对称轴在y轴左,
∴ab>0,即b<0,∴bc<0,∴点P(a,bc)在第三象限,
3.
B
【解答】∵抛物线y=ax2+bx+c(c≠0)过点(-1,0)和点(0,-3),
∴0=a-b+c,-3=c,∴b=a-3,
∵当x=1时,y=ax2+bx+c=a+b+c,∴P=a+b+c=a+a-3-3=2a-6,
∵顶点在第四象限,a>0,∴b=a-3<0,∴a<3,
∴0<a<3,∴-6<2a-6<0,即-6<P<0.
4.
D
【分析】先把不等式整理成x2+1<,然后根据图形找出二次函数图象在反比例函数图象下方部分的x的取值范围即可.
5.
B
【解答】连接BD,AC,
∵菱形ABCD边长为4,∠BAD=60°;∴△ABD与△BCD为正三角形;∴BD=4,AC=4,
△ABE的边AE上的高与△BCF的边CF上的高都为2,∠ADC=120°;
设AE为x,则CF为4-x;
∴S△DEF=ED?DFsin120°=(4-x)[4-(4-x)]
EQ
\F(,2)=﹣
EQ
\F(,4)x2+x,
由图示可知:S△BEF=S菱形ABCD-S△ABE-S△BCF-S△DEF
=×4×4-CF-AE-S△DEF
=8-(CF+AE)-S△DEF=8-4-S△DEF=
EQ
\F(,4)x2-x+4,
根据二次函数的性质,△BEF面积的最小值=﹣
=
EQ
\F(4×
EQ
\F(,4)×4-3,)=3.
6.
2
【解答】方法一:∵a+b2=1,∴a=1-b2,
∴2a2+7b2=2(1-b2)2+7b2
=2b4+3b2+2=2(b2+)2+2-=2(b2+)2+
,
∵b2≥0,∴2(b2+)2
+>0,
∴当b2=0,即b=0时,2a2+7b2的值最小.∴最小值是2.
方法二:∵a+b2=1,∴b2=1-a,
∴2a2+7b2=2a2+7(1-a)=2a2-7a+7=2(a-)2
+,
∵b2≥0,∴1-a≥0,∴a≤1,∴当a=1,即b=0时,2a2+7b2的值最小.∴最小值是2.
7.
±6
【分析】抛物线y=ax2+bx+c的顶点坐标为(﹣,),因为抛物线y=x2-bx+9的顶点在x轴上,所以顶点的纵坐标为零,列方程求解.
8.(1)当y=0时,﹣x2+x+=0,
解之得x1=10,x2=-2(不合题意,舍去),
∴推铅球的水平距离是10米.
(2)y=﹣x2+x+
=﹣(x2-8x+16-16)+
=﹣(x2-8x+16)++
=﹣(x-4)2+3,
当x=4时,y取最大值3,
∴铅球行进高度不能达到4m,最高能达到3m.
9.令y=x2-3x+2,画出其图象如图:
x1=3-≈1.7,x2=3+≈5.3.
10.(1)∵一元二次方程x2+px+q+1=0的一根为2,
∴4+2p+q+1=0,即q=-2p-5.
(2)设一元二次方程x2+px+q+1=0的一根为t,
则由韦达定理,得
2+t=?p
2t=q+1
p=2q
解得,t=0
,p=?2
,q=?1
,
∴原方程的另一根为0.
(3)证明:令x2+px+q=0.则△=p2-4q=p2-4(-2p-5)=(p+4)2+4>0,即△>0,
∴关于x的方程x2+px+q=0有两个不相等的实数根.即抛物线y=x2+px+q与x轴有两个交点.
B组
1.
A
【分析】此题实质是求函数y1=2x-x2和函数y2=的图象在一、四象限有没有交点,根据两个已知函数的图象的交点情况,直接判断.
【解答】设函数y1=2x-x2,函数y2=,
∵函数y1=2x-x2的图象在一、三、四象限,开口向下,顶点坐标为(1,1),对称轴x=1;
函数y2=的图象在一、三象限;而两函数在第一象限没有交点,交点在第三象限.
即方程2x-x2=的正根的个数为0个.
2.
C
【解答】对称轴为直线x=﹣=1,解得b=-2,
∴二次函数解析式为y=x2-2x,即y=(x-1)2-1,
x=-1时,y=1+2=3,
x=4时,y=16-2×4=8,
∵x2+bx-t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当-1≤t<8时,在-1<x<4的范围内有解.
3.
B
【解答】以抛物线所在平面与墙面的交线为y轴,和水平面的交线为x轴建立坐标系.
则由题设条件知,抛物线的顶点M(1,),
A点坐标为(0,10).
于是可设抛物线方程为y=a(x-1)2+.
将A点坐标(0,10)代入该方程可求得a的值为﹣.
∴抛物线方程为:y=﹣(x-1)2+.
令y=0,得(x-1)2=4,∴x=3或-1(舍去).∴B点的坐标为(3,0),故OB=3
m.
4.
C
【解答】∵x=2是方程2x2+ax+b=0的根,∴2×4+2a+b=0,∴2a+b=-8<0,故①正确;
∵x=2是方程2x2+ax+b=0的两个根中较小的根,∴﹣>2+2,>2×2,
∴a<-8,b>8,∴ab<0,故②正确;
∵方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,
∴二次函数y=2x2+ax+b与x轴有两个交点,且对称轴在直线x=2的右边,
∴二次函数y=2x2+ax+b顶点坐标在第四象限,
向上平移2个单位得到二次函数y=2x2+ax+b+2,与x轴不一定有交点,
∴关于x的方程2x2+ax+b+2=0有两个不相等的实数根错误,故③错误;
向下平移2个单位得到二次函数y=2x2+ax+b-2,顶点坐标一定在第四象限,故④正确;
综上所述,正确的结论有①②④共3个.
5.
D
【解答】∵当ax2+bx+c≥0,y=ax2+bx+c(a≠0)的图象在x轴上方,
∴此时y=|ax2+bx+c|=ax2+bx+c,
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象,
∵当ax2+bx+c<0时,y=ax2+bx+c(a≠0)的图象在x轴下方,
∴此时y=|ax2+bx+c|=-(ax2+bx+c)
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象,
∵y=ax2+bx+c(a≠0)的顶点纵坐标是-3,
∴函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象的顶点纵坐标是3,
∴y=|ax2+bx+c|的图象如图,
∵观察图象可得当k≠0时,
函数图象在直线y=3的上方时,纵坐标相同的点有两个,
函数图象在直线y=3上时,纵坐标相同的点有三个,
函数图象在直线y=3的下方时,纵坐标相同的点有四个,
∴若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,
则函数图象应该在y=3的上边,故k>3.
6.1(在-2<b<2范围内的任何一个数)
【解答】把(0,-3)代入抛物线的解析式得:c=-3,∴y=x2+bx-3,
∵使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,
∴把x=1代入y=x2+bx-3得:y=1+b-3<0
把x=3代入y=x2+bx-3得:y=9+3b-3>0,
∴-2<b<2,
即在-2<b<2范围内的任何一个数都符合.
7.
3
【解答】设P、Q同时出发后经过的时间为t
s,四边形APQC的面积为S
mm2,
则有:S=S△ABC-S△PBQ=×12×24-×4t×(12?2t)
=4t2-24t+144
=4(t-3)2+108.
∵4>0∴当t=3s时,S取得最小值.
8.(1)依题意:x1+x2=-m,x1x2=m-1,
∵x12+x22+x1x2=7,∴(x1+x2)2-x1x2=7,
∴(-m)2-(m-1)=7,即m2-m-6=0,解得m1=-2,m2=3,
∵c=m-1<0,∴m=3不合题意,∴m=-2,∴抛物线的解析式是y=x2-2x-3.
(2)能.理由如下:
如图,设P是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
若∠POC=∠PCO,则PD应是线段OC的垂直平分线,
∵C的坐标为(0,-3),∴D的坐标为(0,-),
∴P的纵坐标应是-
,
令x2-2x-3=-,解得,x1=
EQ
\F(2?,2),x2=
EQ
\F(2+,2),
∴所求点P的坐标是(
EQ
\F(2?,2),-),(
EQ
\F(2+,2),-).
9.(1)∵抛物线y=﹣x2+bx+c,经过点A(0,-4),∴c=-4,
又∵由题意可知,x1、x2是方程﹣x2+bx+c的两个根,∴x1+x2=b,x1x2=6,
由已知得(x2-x1)2=25,
又∵(x2-x1)2=(x2+x1)2-4x1x2=b2-24,∴b2-24=25,解得b=±,
当b=时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.∴b=﹣.
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,
又∵y=﹣x2﹣x﹣4=﹣(x+)2+,
∴抛物线的顶点(-,)即为所求的点D.
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),根据菱形的性质,点P必是直线x=-3与抛物线y=﹣x2﹣x﹣4
的交点,
∴当x=-3时,y=﹣×(-3)2﹣×(-3)﹣4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形.
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上.
10.(1)∵x1,x2是方程x2-2(m-1)x+m2-7=0的两个根,
∴x1+x2=2(m-1),x1?x2=m2-7.
又∵x12+x22=10,∴(x1+x2)2-2x1x2=10,
∴[2(m-1)]2-2(m2-7)=10,即m2-4m+4=0.解得:m1=m2=2.
将m=2代入方程x2-2(m-1)x+m2-7=0,得:x2-2x-3=0,解得:x1=-1,x2=3.
∴点A的坐标为(-1,0),点B的坐标为(3,0).
(2)因为抛物线与x轴的交点为A(-1,0)、B(3,0),由对称性可知,顶点M的横坐标为1,则顶点M的坐标为(1,-4).
∴
a?b+c=0
9a+3b+c=0
a+b+c=?4
解得:a=1,b=?2,c=?3,
∴抛物线的解析式为y=x2-2x-3.
在y=x2-2x-3中,令x=0,得y=-3.∴点C的坐标为(0,-3).
(3)设抛物线的对称轴与x轴交于点D,
则AO=OD=1,DB=2,OC=3,
DM=4,AB=4.
∴S四边形ACMB=S△ACO+S梯形OCMD+S△DMB
=?AO?CO+(CO+MD)+DB?MD
=×1×3+×(3+4)×1+×2×4=9.
设P(x0,y0)为抛物线上一点,
则S△PAB=AB?|y0|.
若S△PAB=2S四边形ACMB,则?AB?|y0|=18,
∴丨y0丨=9,y0=±9.
将y0=9代入y=x2-2x-3中,得x2-2x-3=9,即x2-2x-12=0,
解得:x1=1-,x2=1+.
将y0=-9代入y=x2-2x-3中,得:x2-2x-3=-9,
即x2-2x+6=0.
∵△=(-2)2-4×1×6=-20<0,
∴此方程无实数根.
∴符合条件的点P有两个:P1(1-,9),P2(1+,9).
五、优化提高
1.②④
【解答】∵抛物线与x轴的交点为(1,0)和(x1,0),-2<x1<-1,与y轴交于正半轴,
∴a<0,
∵-2<x1<-1,∴﹣<﹣<0,∴b<0,b>a,故①错误,③错误;
∵抛物线与x轴有两个交点,∴b2-4ac>0,∴ac<b2,故②正确;
∵抛物线与x轴的交点有一个为(1,0),∴a+b+c=0,∴b=-a-c,
∵b<0,b>a(已证),∴-a-c<0,-a-c>a,∴c>-a,c<-2a,
∴-a<c<-2a,故④正确,
综上所述,正确的结论有②④.
2.
∵二次函数y=-x2+2x-2=-(x-1)2-1,∴开口向下,对称轴为x=1,
当t+1<1,即t<0时,
函数y的最小值是-t2+2t-2,最大值为-(t+1)2+2(t+1)-2=-t2+1;
当t≤1≤t+1,即0≤t≤1时,
函数y的最小值是-t2+2t-2,最大值为-1;
当t>1时,
函数y的最大值是-t2+2t-2,最小值为-t2+1.
3.
当△ABC为直角三角形时,过C作CE⊥AB于E,则AB=2CE.
∵抛物线与x轴有两个交点,∴△=b2
-4ac>0,则|b2-4ac|=b2-4ac.
∵a>0,∴AB=
EQ
\F(,|a|)
=
EQ
\F(,a)
,
又∵CE=||=,
∴
EQ
\F(,a)
=2×,
∴=,
∴b2-4ac=,
∵b2-4ac>0,∴b2-4ac=4.
(2)当△ABC为等边三角形时,
由(1)可知CE=
EQ
\F(,2)AB,
∴=
EQ
\F(,2)×
EQ
\F(,a)
,
∵b2-4ac>0,∴=,∴b2-4ac=12.
4.(1)∵抛物线y=ax2+bx+8经过点A(-6,0),B(4,0),
∴
36a?6b+8=0
16a+4b+8=0
解得a=﹣,b=﹣,∴抛物线的解析式是:y=﹣x2﹣x+8.
(2)如图①,作DM⊥抛物线的对称轴于点M,设G坐标为(-1,n),
由翻折的性质,可得BD=DG,
∵B(4,0),C(0,8),点D为BC的中点,
∴点D的坐标是(2,4),
∴点M的坐标是(-1,4),DM=2-(-1)=3,
∵B(4,0),C(0,8),∴BC==4,∴BD=2,
在Rt△GDM中,32+(4-n)2=20,解得n=4±,
∴G点的坐标为(-1,4+)或(-1,4-).
(3)抛物线y=ax2+bx+8对称轴上存在F,使得以C、D、E、F为顶点的四边形为平行四边形.
①当CD∥EF,且点E在x轴的正半轴时,如图②,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得,c=1,d=4,∴点F的坐标是(-1,4),E坐标是(1,0).
②当CD∥EF,且点E在x轴的负半轴时,如图③
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得c=?3
,d=?4
,
∴点F的坐标是(-1,-4),点E的坐标是(-3,0).
③当CE∥DF时,如图④,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(-1,d),
则
=
=
解得c=3
,d=12
,
∴点F的坐标是(-1,12),点E的坐标是(3,0).
综上,可得抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,点F的坐标是(-1,4)、(-1,-4)或(-1,12).
简记“左同右异”
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
