4.4整式 教学课件(共24张PPT)

整式
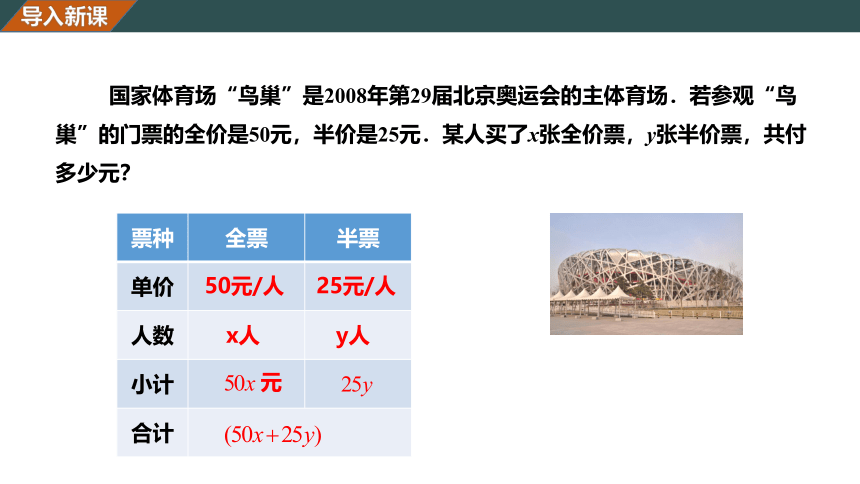
国家体育场“鸟巢”是2008年第29届北京奥运会的主体育场．若参观“鸟巢”的门票的全价是50元，半价是25元．某人买了x张全价票，y张半价票，共付多少元？
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}票种
全票
半票
单价
人数
小计
合计
50元/人
25元/人
x人
y人
元
导入新课
-3x ，2a2 ，ab ，
这些代数式是怎样组成的？有什么共同特点？
由数与字母或字母与字母相乘组成的代数式叫做单项式．
注意：
1、单独一个数或一个字母也叫单项式．如0，-1，a ．
2、分母中不含字母，也不含字母开方的运算（根号内不含字母）．
合作学习
-2a2b2
-2
2
2
单项式中的数字因数叫做这个单项式的系数．
例如，-3x的系数是-3，ab的系数是1．
一个单项式中所有字母的指数的和叫做这个单项式的次数．
例如，-3x的次数是1 ，ab的次数是1+1=2．
总结
几点说明：
①常数项的次数规定为零；
②圆周率π是常数；
③当一个单项式的系数是1或-1时，1通常省略不写；
④单项式的系数是带分数时，通常写成假分数．
总结
{2D5ABB26-0587-4C30-8999-92F81FD0307C}单项式
-2xy
a3bc
系数
次数
-2
2
1
5
2
3
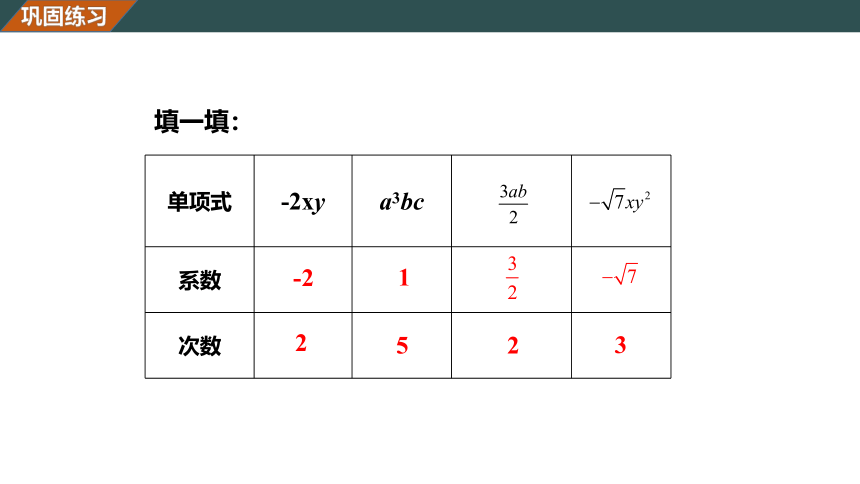
填一填：
巩固练习
50x+25y 、2x+y、a2-b2+3、 50-3a、10y+x．
这些代数式是怎样组成的？和前面给出的代数式相比，有什么特点？
由几个单项式相加组成的代数式叫做多项式．
21cnjy
合作学习
-3x + 2a2 + ab2 +5
在多项式中，每个单项式叫做多项式的项．如-3x + 2a2 + ab2 +5的项有-3x 、 2a2 、 ab2 、 5．
不含字母的项叫做常数项．如-3x + 2a2 + ab2 +5的常数项是 5．
次数最高的项的次数就是这个多项式的次数．
如-3x + 2a2 + ab2 +5次数最高的项ab2 的次数是3．多项式-3x + 2a2 + ab2 +5称为三次四项式．
-3x
2a2
ab2
5
5
ab2
21cnjy.com
合作学习
单项式和多项式统称整式．
注意：
①多项式的次数不是所有项的次数之和，而是最高次项的次数；
②多项式的每一项都包括它前面的符号．
疑问：整式与代数式的关系是什么？
整式一定是代数式，代数式不一定是整式
总结
指出下列多项式的项和次数，并说明它们是几次几项式？
（1）x5-x2-1；
（2）-a2-b2；
解：（1）x5-x2-1的项是x5，-x2，-1，次数是5，是五次三项式；
（2）-a2-b2的项是-a2，-b2，次数是2，是二次二项式；
21cnjy
巩固练习
例 一个花坛的形状如图，它的两端是半径相等的半圆，求:
（1）花坛的周长l．
（2）花坛的面积S．
解：（1）l=2a+2πr ．
（2）花坛的面积是一个长方形的面积与两个半圆的面积之和，即S=2ar+πr2．
2a+2πr，2ar+πr2，分别是几次多项式？分别由哪些项组成？每一项的系数是什么？
2a+2πr是一次多项式，由2a和2πr两项组成，系数分别是2，2π．
2ar+πr2是二次多项式，由2ar和πr2两项组成，系数分别是2，π．
21cnjy.com
例题讲解
1．单项式4xy2z3的次数是（　　）
A．3 B．4 C．5 D．6
【分析】单项式的次数是指各字母的指数之和
解：该单项式的次数为：1+2+3=6，故选D.
课后练习
2．x2y3﹣3xy2﹣2次数和项数分别是（　　）
A．5，3 B．5，2 C．2，3 D．3，3
【分析】利用多项式的定义求解即可．
解：x2y3﹣3xy2﹣2次数和项数分别是5，3．故选：A．
课后练习
3．若A与B都是二次多项式，则A﹣B：（1）一定是二次式；（2）可能是四次式；（3）可能是一次式；（4）可能是非零常数；（5）不可能是零．上述结论中，不正确的有（　　）个．
A．5 B．4 C．3 D．2　
【分析】多项式相减，也就是合并同类项，合并同类项时只是把系数相加减，字母和字母的指数不变，所以结果的次数一定不高于2次，由此可以判定正确个数．
课后练习
解：∵多项式相减，也就是合并同类项，
而合并同类项时只是把系数相加减，字母和字母的指数不变，
∴结果的次数一定不高于2次，
当二次项的系数相同时，合并后结果为0，
所以（1）和（2）（5）是错误的．故选C．
课后练习
3．若A与B都是二次多项式，则A﹣B：（1）一定是二次式；（2）可能是四次式；（3）可能是一次式；（4）可能是非零常数；（5）不可能是零．上述结论中，不正确的有（　　）个．
A．5 B．4 C．3 D．2　
4.⑴写出一个单项式，使它的系数是 2，次数是 3.
⑵写出一个多项式，使它的项数是 3，次数是 4.
（答案不唯一）
课后练习
5.用代数式表示下列各题：
1． y的-3倍是_______．
2． 长方形的长是a，宽是b，那么长方形的面积是_______．
3．商店里卖出a台电脑，每台b+2元，商店共获利_______元．
-3y
ab
a(b+2）
4 ．a与b 的平方和与3的差 .
a2+b2-3
课后练习
6.对于多项式(n－1)xm＋2－3x2＋2x(其中m是大于－2的整数)．
（1）若n＝2，且该多项式是关于x的三次三项式，求m的值；
（2）若该多项式是关于x的二次单项式，求m，n的值；
（3）若该多项式是关于x的二次二项式，则m，n要满足什么条件？
（1）解：由于n＝2，且该多项式是关于x的三次三项式，
故原式＝xm＋2－3x2＋2x，
由题意得m＋2＝3，
解得m＝1
分析：（1）将n=2代入代数式，再根据该多项式是关于x的三次三项式，可得出m+2=3，解方程求解即可。
课后练习
6.对于多项式(n－1)xm＋2－3x2＋2x(其中m是大于－2的整数)．
（1）若n＝2，且该多项式是关于x的三次三项式，求m的值；
（2）若该多项式是关于x的二次单项式，求m，n的值；
（3）若该多项式是关于x的二次二项式，则m，n要满足什么条件？
（2）解：若该多项式是关于x的二次单项式，
则m＋2＝1，n－1＝－2，解得m＝－1，n＝－1
分析：（2）根据已知该多项式是关于x的二次单项式，可得出关于m、n的方程求解即可。
课后练习
6.对于多项式(n－1)xm＋2－3x2＋2x(其中m是大于－2的整数)．
（1）若n＝2，且该多项式是关于x的三次三项式，求m的值；
（2）若该多项式是关于x的二次单项式，求m，n的值；
（3）若该多项式是关于x的二次二项式，则m，n要满足什么条件？
（3）解：分三种情况：
①n＝1，m为任意实数；
②m＝－1，n≠－1；
③m＝0，n≠4.
分析：（3）由该多项式是关于x的二次二项式，可分情况讨论：①n＝1，m为任意实数；②m＝－1，n≠－1；③m＝0，n≠4，可解答。
课后练习
7.已知单项式3x2yn的次数为5，多项式 的次数为6，求单项式（m+n）xmyn的次数与系数的和．
解：∵单项式3x2yn的次数为5，多项式 的次数为6，
∴2+n=5，2+m+3=6，
解得：m=1，n=3，
∴（m+n）xmyn=4xy3，
系数是4，次数是1+3=4，4+4=8，
即单项式（m+n）xmyn的次数与系数的和是8．
课后练习
单项式：由数与字母或字母与字母相乘组成的代数式．
单项式中的数字因数叫做这个单项式的系数．
一个单项式中所有字母的指数的和叫做这个
单项式的次数．
多项式：由几个单项式相加组成的代数式
在多项式中，每个单项式叫做多项式的项．
不含字母的项叫做常数项．
次数最高的项的次数就是这个多项式的次数．
整式
课后总结
课后作业
教材练习题
谢
谢
观
看