3.2实数 教学课件(共26张PPT)

实数
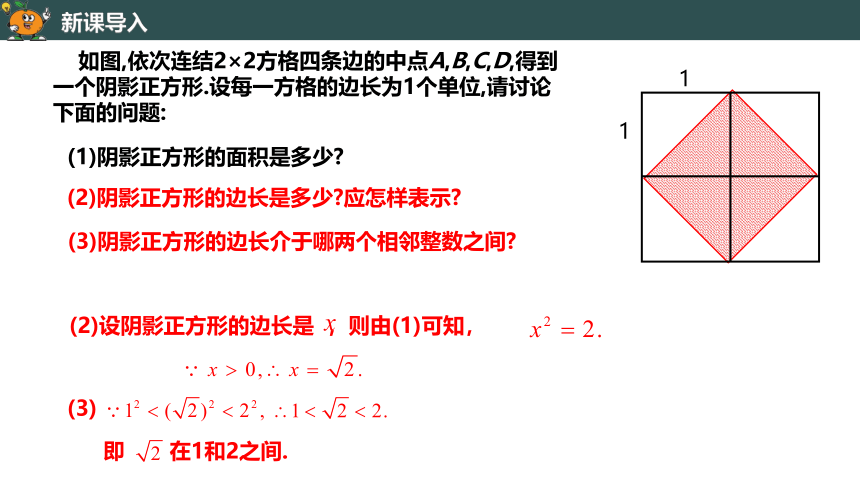
如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形.设每一方格的边长为1个单位,请讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?
答：阴影正方形的面积为2.
1
1
新课导入
如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形.设每一方格的边长为1个单位,请讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?
(2)设阴影正方形的边长是 ，则由(1)可知，
(3)
即 在1和2之间.
1
1
新课导入
到底是一个什么样的数？
不是
(2) 是分数吗？
不是
想一想
探究
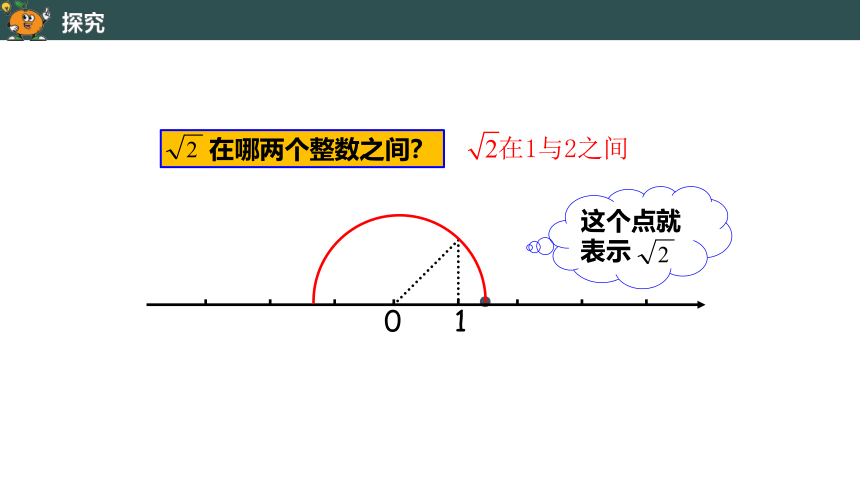
在哪两个整数之间？
0
1
这个点就表示
探究
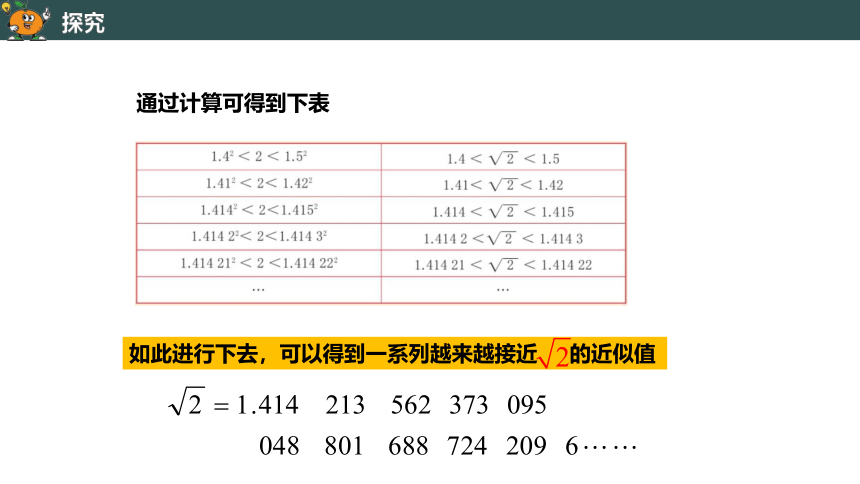
通过计算可得到下表
如此进行下去，可以得到一系列越来越接近 的近似值
探究
无理数
归纳
无理数广泛存在着，无理数一般有三种情况：
①如 等，但 等是有理数；
③1.010010001…（两个1之间依次多一个0），
95.6868868886…（两个6之间依次多一个8）等.
② 等；
如果我们把整数看做小数部分为零的有限小数，那么有理数便是有限小数与无线小数的统称.
和有理数一样，无理数也可以分为正无理数和负无理数
归纳
无理数的常见类型：
归纳
（1）开不尽的方根
（2）与π相关的数
（3）似循环但实际不循环，形如“1.010010001…” (两个“1”之间依次多一个0)的数
属于有理数的：
属于无理数的：
属于实数的有：
属于分数的有：
练习
分数
无理数常有的表现形式:
开方开不尽根的根号式
及
π
实数的分类：
实数
有理数
无理数
整数
正整数
零
负整数
(可化为有限小数或无限循环小数)
(无限不循环小数)
实数
有理数和无理数统称为实数
归纳
把数从有理数扩充到实数以后，有理数的相反数和绝对值的概念同样适用于实数。
例如： 和 互为相反数
归纳
　 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
?
?
数轴上的每一个点都表示一个有理数么？否
练习
每一个有理数都可以用数轴上的点来表示，例如把-2，-0.5，????????和2表示在数轴上。
?
0
1
-1
如图:OA=OB=OC,数轴上A、C对应的数是什么?
B
A
C
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。
练习
有理数的大小比较法则也适用于实数
在数轴上表示的两个实数，右边的数总比左边的数大
归纳
?
?
?
例题讲解
1.下列各数中无理数为（　　）
?
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
A
课后练习
, , , , ,
2.把下列各数表示在数轴上：
0
－1
2
3
1
－2
－3
4
课后练习
3.填空：
（1） 的相反数是__________
（2） 的相反数是 .
（3） ___________
（4）绝对值等于 的数是 _________

课后练习
课后练习
⑴ -1
⑵
⑶ 3
⑷
4.比较大小：
解：
所以6的算术平方根在2和3之间，与3比较接近。
5、不用计算器，判断6的算术平方根在哪两个整数之间，与哪个整数比较接近，请写出你的判断过程。
课后练习
(1)你能将这个问题转化为数学问题吗？
(2)如何求出长方形的长和宽？
(3)长方形的长和宽与正方形的边长之间的大小关系是什么？
(4)小丽能用这块纸片裁出符合要求的纸片吗？
4、 小丽想用一块面积为400cm2为的长方形纸片，沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2．
课后练习
解：设长方形纸片的长为3x cm，宽为2x cm.根据边长与面积的关系得
3x ? 2x=300 ，
6x2=300 ，
x2=50，
　 ，
故长方形纸片的长为 ，宽为 　 ．
因为50＞49，得 ＞7，所以 ＞3×7=21，比原正方形的边长更长，这是不可能的．所以，小丽不能用这块纸片裁出符合要求的纸片．
课后练习
实数的分类
课后小结
教材练习题
课后作业
谢
谢
观
看