浙教版九年级上册数学 第8讲 圆心角与圆周角同步学案(含答案)
文档属性
| 名称 | 浙教版九年级上册数学 第8讲 圆心角与圆周角同步学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 913.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 19:09:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第8讲、圆心角与圆周角
一、课前检测
(一)选择题(共4小题)
1.
若和的度数相等,则下列命题中,正确的是(
)
A.=
B.与的长度相等
C.所对的弦和所对的弦相等
D.所对的圆心角与所对的圆心角相等
2.
如图,点O是两个同心圆的圆心,大圆的半径OA,OB分别交小圆于点C,D.下列结论中正确的个数有( )
①∠OCD=∠OAB;
②AB=CD;
③=
A.0个
B.1个
C.2个
D.3个
3.
如图,A,D是⊙O上的两点,BC是直径.若∠D=35°,则∠OCA的度数是( )
A.35°
B.55°
C.65°
D.70°
第3题
第4题
4.
如图,∠1,∠2,∠3,∠4的大小关系是(
)
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
(二)填空题(共2小题)
5.
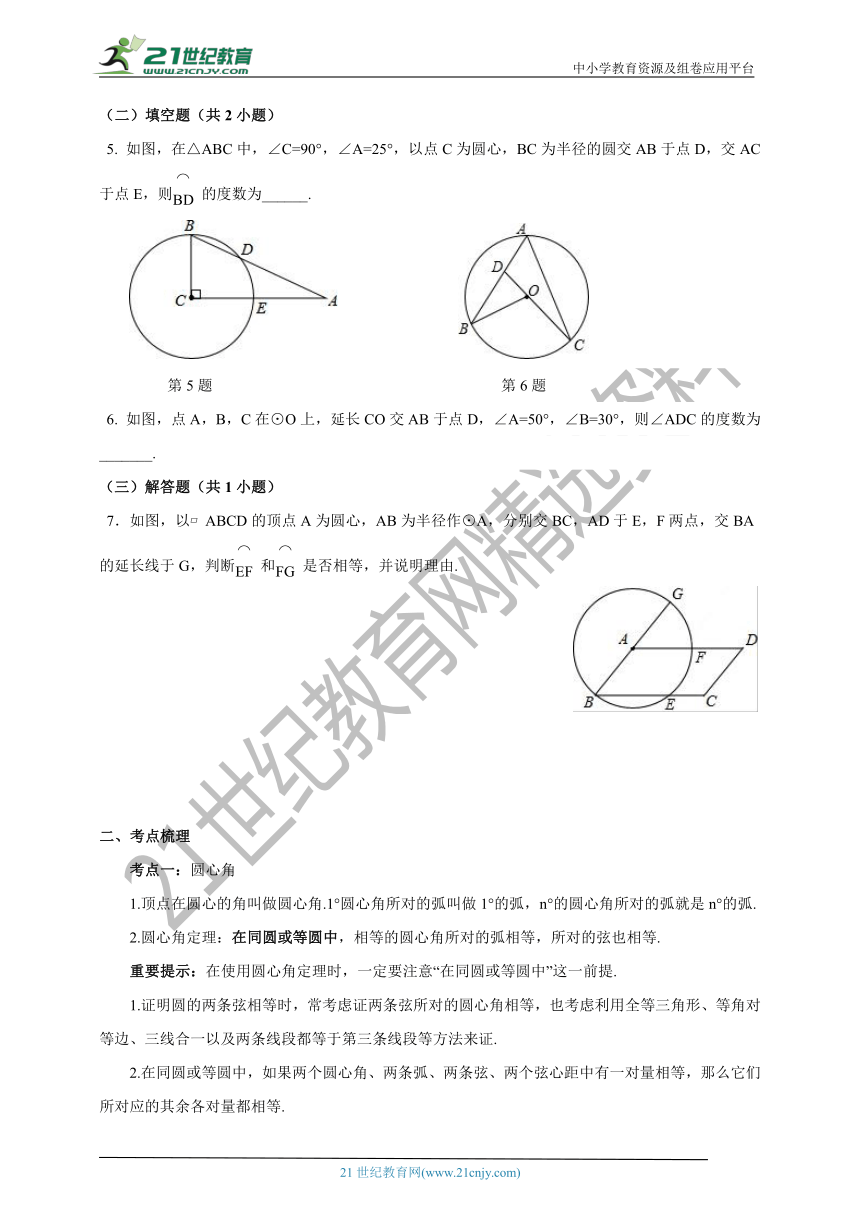
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为______.
第5题
第6题
6.
如图,点A,B,C在⊙O上,延长CO交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为_______.
(三)解答题(共1小题)
7.如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断和是否相等,并说明理由.
二、考点梳理
考点一:圆心角
顶点在圆心的角叫做圆心角.1°圆心角所对的弧叫做1°的弧,n°的圆心角所对的弧就是n°的弧.
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
重要提示:在使用圆心角定理时,一定要注意“在同圆或等圆中”这一前提.
1.证明圆的两条弦相等时,常考虑证两条弦所对的圆心角相等,也考虑利用全等三角形、等角对等边、三线合一以及两条线段都等于第三条线段等方法来证.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
考点二:圆周角
顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
圆周角的两个特征:(1)角的顶点在圆上;(2)角的两边都与圆相交.
在同圆或等圆中,同弧或等弧所对的圆周角相等(都等于该弧所对的圆心角的一半);相等的圆周角所对的弧也相等.
三、重点突破
重点一:圆心角
例1.已知⊙O的半径为5cm,弦AB的长为5cm,则弦AB所对的圆周角的度数是_______.
(点拨:根据题意画出图形,有两个角)
例2.如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,求的度数.
(点拨:连结CD)
例3.
如图,已知AB,CD是⊙O的两条直径,BE是⊙O的弦,且BE∥CD.求证:=
.
(点拨:需推知∠AOC=∠COE即可)
例4.
如图所示,△ABC为等边三角形,BC为⊙O的直径,⊙O分别与AB、AC相交于D、E.
求证:(1)==.
(2)AD=DB,AE=EC.
例5.如图,已知AB是⊙O的直径,M,N分别是OA,OB的中点,CM⊥AB,DN⊥AB.求证:=.
(点拨:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等)
重点二:圆周角
例1.已知:如图,BC为⊙O的直径,BF为弦,A为的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
(点拨:垂径定理,直角三角形的性质以及弧、弦的关系)
例2.如图,△ABC是⊙O的内接三角形,C是优弧AB上的一点(点C不与点A,B重合).设∠OAB=α,∠C=β.
(1)当α=36°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
例3.如图,在△ABC中,AB=AC,∠BAC=40°.以AB为直径的半圆分别交AC,BC于点E,D,求,及的度数.
(点拨:在同圆或等圆中,圆周角的度数等于它所夹弧所对的圆心角度数的一半)
例4.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
(点拨:圆周角定理)
例5.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,,∠APC=∠CPB=60°.
(1)判断△ABC的形状;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
(点拨:在PC上截取PD=AP)
四、经典练习
A组
(一)选择题(共3小题)
1.
已知,是同圆中的两段弧,且=2,则弦AB与CD的关系是(
)
A.AB=2CD
B.AB<2CD
C.AB>2CD
D.不能确定
2.
已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧的中点,若△POC为直角三角形,则PB的长度( )
A.1
B.5
C.1或5
D.2或4
3.
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为(
)
A.cm
B.3cm
C.cm
D.9cm
(二)
填空题(共4小题)
4.
如图,△ABC是⊙O的内接三角形,∠B=40°,点P在劣弧AC上移动(点P与点A、C不重合),则∠α的变化范围是________.
第4题
第5题
5.
如图,游乐园的大观览车半径为25米,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟,某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是_________米(观览处最低处距地面的高度忽略不计).
6.
如果一条弦将圆分成两段弧,它们的度数之比为3:1,那么此弦的弦心距的长度与与此弦的长度的比为_________.
7.
圆的一条弦把圆分成5:1两部分,如果圆的半径是2cm,那么这条弦的长是______cm.
(三)解答题(共3小题)
8.
如图,已知△ABC内接于⊙O,点A,B,C把⊙O三等分.
(1)试判断△ABC的形状,并说明理由;
(2)求∠AOB的度数.
9.
如图,在⊙O中半径OA⊥OB,C,D是弧AB的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.
10.
如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F是AC上的一点,AB=AD,∠BFC=∠BAD=2∠DFC.求证:
(1)CD⊥DF;
(2)BC=2CD.
B组
(一)选择题(共4小题)
1.如图,在菱形ABCD中,AC=AB,以顶点B为圆心,以AB长为半径画圆,延长DC交⊙B于点E,则的度数为( )
A.120°
B.90°
C.60°
D.30°
第1题
第3题
第4题
2.若⊙O内的一条弦与直径相交成30°的角,并把直径分成2cm和6cm两段,则这条弦的弦心距为(
)
A.1cm
B.2cm
C.3cm
D.4cm
3.
如图,AB为⊙O的直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P(
)
到CD的距离保持不变
B.位置不变
C.等分
D.随点C的移动而移动
4.
如图,△ABC是⊙O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线分别交⊙O于点D,E,且BD=CE,则∠A等于( )
A.90°
B.60°
C.45°
D.30°
(二)填空题(共4小题)
5.
如图,用四个边长为1的小正方形拼成一个大正方形,A,B,O是小正方形的顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB的度数为_______.
第5题
第6题
6.
如图,AB,CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于点P,则∠P的度数为________.
7.
如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
第7题
第8题
8.
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为________.
(三)解答题(共3小题)
9.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB于点E.试判断四边形EBCM的形状,并加以证明.
10.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM、ON,求∠MON的度数.
(2)图②、③、…④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、…正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是_______,图③中∠MON的度数是_______;…由此可猜测在n边形图中∠MON的度数是_______.
五、优化提高
1.
如图,扇形OAB的圆心角为124°,C是弧上一点,则∠ACB=______.
2.
已知:点A(0,4),B(0,-6),C为x轴正半轴上一点,且满足∠ACB=45°,则点C坐标为________.
3.
已知AB是⊙O的直径,C是圆周上的动点,P是的中点.
(1)如图1,求证:OP∥BC;
(2)如图2,PC交AB于D,当△ODC是等腰三角形时,求∠A的度数.
4.
已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,=,求证:△PMN是等腰三角形.
5.
我们把1°的圆心角所对的弧叫做1°的弧.则圆心角AOB的度数等于它所对的弧AB的度数记为:∠AOB=.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图1给予证明(不要求写己知、求证.只需直接证明),并解决以下的问题(1)和问题(2).
问题(1):如图2,⊙0的两条弦AB、CD相交于圆内一点P,求证:∠APC=(+);
问题(2):如图3,⊙0的两条弦AB、CD相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明)
参考答案
一、课前检测
1.
D
2.
B【解答】①∵OC=OD,OA=OB,
∴∠OCD=,∠OAB=,
∴∠OCD=∠OAB,故①正确;
②∵CD<AB,故②错误;
③∵与不是等圆或同圆中的弧,
∴≠,故③错误.
3.
B【解答】∵∠AOC=2∠D,∠D=35°,
∴∠AOC=2∠D=2×35°=70°,
在等腰△OAC中,∵OA=OC,∠AOC=70°,
∴∠OCA==55°.
4.
B【解答】如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,
根据三角形的外角的性质得:∠5>∠4,∠2>∠6,
∴∠4<∠1=∠3<∠2.
5.
50°【解答】连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴的度数为50°.
6.
110°【解答】∵∠A=50°,
∴∠BOC=2∠A=100°,
∵∠B=30°,∠BOC=∠B+∠BDC,
∴∠BDC=∠BOC-∠B=100°-30°=70°,
∴∠ADC=180°-∠BDC=110°.
7.【解答】=,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴=.
三、重点突破
重点一:圆心角
例1.
30°或150°
【解答】如图:在优弧AB上取点C,连接AC,BC,在劣弧上取点D,连接AD,BD,
∵⊙O的半径为5cm,弦AB的长为5cm,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠C=∠AOB=30°,
∴∠D=180°-∠C=150°.
∴弦AB所对的圆周角的度数是:30°或150°.
例2.
52°【解答】连结CD,如图,
∵∠C=90°,∠A=26°,
∴∠B=64°,
∵CB=CD,
∴∠CDB=∠B=64°,
∴∠BCD=180°-64°-64°=52°,
∴的度数为52°.
例3.【解答】证明:连接OE,
∵BE∥CD,
∴∠COE=∠E,∠BOD=∠B,
∵OB=OE,
∴∠B=∠E,
∴∠COE=∠BOD,
∵∠AOC=∠BOD,
∴∠AOC=∠COE,
∴=
.
例4.【解答】(1)如图所示,连接OD,OE,
∵OB=OD=OE=OC,∠B=∠C=60°
∴△BOD与△COE都是等边三角形
∴∠BOD=∠COE=60°
∠DOE=180°-∠BOD-∠COE=60°
∴∠DOE=∠BOD=∠COE
∴==.
(2)连接BE,CD,
∵∠BOD=∠COE=60°
∴∠BCD=30°,∠EBC=30°,
∴DC平分∠ACB,BE平分∠ABC,
∴AD=DB,AE=EC.
例5.【解答】证明:连结OC、OD,如图,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°,
在Rt△OMC和Rt△OND中,OM=ON,OC=OD,
∴Rt△OMC≌Rt△OND(HL),
∴∠COM=∠DON,
∴=.
重点二:圆周角
例1.【解答】证明:连AF,AB,AC.
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠BAD=∠C,
∵∠C=∠F,
∴∠BAD=∠F,
∵A为的中点,
∴∠ABF=∠F,
∴∠BAD=∠ABF,
∴BE=AE.
例2.【解答】(1)连OB,则OA=OB,
∴∠OBA=∠OAB=36°
∴∠AOB=180°-∠OAB-∠OBA=108°
∴β=∠C=∠AOB=54°;
(2)α与β之间关系是α+β=90°.
证明:连OB,则OA=OB,
∴∠OBA=∠OAB=α
∴∠AOB=180°-2α
∴β=∠C=∠AOB=(180°-2α)=90°-α.
∴α+β=90°.
例3.【解答】连接BE、AD,
∵AB是圆的直径,
∴∠ADB=∠AEB=90°,
∴∠ABE=90°-40°=50°,
AD⊥BC,
∵AB=AC,∠BAC=40°,
∴∠BAD=∠DAC=∠BAC=20°,
∴由圆周角定理得:弧BD所对的圆心角的度数是2∠DAB=40°,
弧DE所对的圆心角的度数是2∠DAE=40°,
弧AE的度数是180°-40°-40°=100°
例4.【解答】(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2.
例5.【解答】(1)△ABC是等边三角形.
证明如下:在⊙O中
∵∠BAC与∠CPB是弧BC所对的圆周角,∠ABC与∠APC是弧AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;故答案为:等边三角形;
(2)在PC上截取PD=AP,如图,
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,∠APB=∠ADC,∠ABP=∠ACD,AP=AD,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP
四、经典练习
A组
1.
B【解答】取的中点E,连接AE、BE,
∴弧AE=弧BE,
∵=2,
∴∠AOB=2∠COD,
∴弧AE=弧BE=弧CD,
∵AE+BE>AB,
∴2CD>AB,
∴AB<2CD.
2.
C【解答】∵点C是劣弧的中点,
∴OC垂直平分AB,
∴DA=DB=3,
∴OD==1,
若△POC为直角三角形,只能是∠OPC=90°,
则△POD∽△CPD,
∴,
∴PD2=4×1=4,
∴PD=2,
∴PB=3-2=1,
根据对称性得,
当P在OC的左侧时,PB=3+2=5,
∴PB的长度为1或5.
3.
B
【解答】∵∠CDB=30°,
∴∠COB=30°×2=60°.
又∵⊙O的半径为cm,
∴CE=sin60°=×=,
∴CD=×2=3(cm).
4.
0°<α<80°【解答】∵点P在劣弧
AC上移动,
∴当点P与点C重合时,α最小值=0°;
而∠AOC=2∠B=80°(同弧所对的圆周角是所对的圆心角的一半),
当点P与点A重合时,α最大值=∠AOC=80°,
∵点P不与点A、C重合,
∴α的变化范围是0°<α<80°.
5.
【解答】根据题意,可知:此人运动到了圆的三等分点处,设为点B,则∠AOB=120°,
作BC⊥AD于C,OE⊥BC于E,则CE=OA=25m,
在Rt△BOE中,根据30°所对的直角边是斜边的一半,得BE=m,
则此人距地面AD的高度是米.
6.
1:2
7.2【解答】连接OA,OB,过O作OD⊥AB.
∵一条弦把圆分成5:1两部分,
∴∠AOB=60°,
∴∠2=∠1=30°;
又∵OD⊥AB,OA=2cm,
∴AD=OA=1cm,
∴AB=2AD=2cm.
8.【解答】(1)△ABC为等边三角形;
∵△ABC内接于圆O,点A,B,C把圆O的周长三等分,
∴弧AB=弧AC=弧BC,
∴AB=AC=BC,
∴△ABC为等边三角形;
(2)∵弧AB=弧AC=弧BC,
∴∠BOC=∠AOC=∠AOB,
∴∠AOB=360°÷3=120°.
9.
【解答】连接AC、BD,
∵C,D是弧AB的三等分点,
∴AC=CD=BD,∠AOC=∠COD,OA=OC=OD,
在△ACO与△DCO中,
∵OA=OD,∠AOC=∠DOC,OC=OC,
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC,
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD,
∴AE=BF=CD.
10.
【解答】证明:(1)∵AB=AD,
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°-∠BAD)÷2=90°-∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF.
(2)过F作FG⊥BC于点G,
∵∠ACB=∠ADB,
又∵∠BFC=∠BAD,
∴∠FBC=∠ABD=∠ADB=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,∠GFC=∠BAD=∠DFC,
∵在△FGC和△DFC中,∠GFC=∠DFC,FC=FC,∠ACB=∠ACD,
∴△FGC≌△DFC(ASA),
∴CD=GC=BC.
∴BC=2CD.
B组
1.
C【解答】连接OE,
∵四边形ABCD是菱形,∴AB∥CD,AB=BC,
∵AC=AB,∴△ABC是等边三角形,
∴∠ABC=60°,∴∠BCE=∠ABC=60°,
∵BE=BC,
∴△BCE是等边三角形,∴∠EBC=60°,
∴的度数为60°.
2.
A
【解答】
∵AF=2cm,BF=6cm,∴OF=2cm,
∵∠OEF=90°,∠EFO=30°,
∴OE=1cm,
3.
B【解答】不发生变化.
连接OP,
∵OP=OC,
∴∠P=∠OCP,
∵∠OCP=∠DCP,
∴∠P=∠DCP,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB,
∴弧AP=弧BP,
∴点P为弧AB的中点不变.
4.
B【解答】连接AD、BE,
∵BD=CE
∴弧BD=弧CE,∴∠BAD=∠EBC,
∵∠BAD=∠CAD+∠CAB,∠EBC=∠ABE+∠ABD+∠CBD,
∴∠CAD+∠CAB=∠ABE+∠ABD+∠CBD,
∵∠CAD=∠CBD(同圆中,同弧所对的圆周角相等),
∴∠CAB=∠ABD+∠ABE,
∵∠ABE=∠ACE(同圆中,同弧所对的圆周角相等),
∴∠CAB=∠ABD+∠ACE(等量代换)
∵BD、CE分别平分∠ABC、∠ACB,
∴∠ABD=∠ABC,∠ACE=∠ACB
∴∠CAB=(∠ABC+∠ACB),∴∠ABC+∠ACB=2∠CAB
∵∠CAB+∠ABC+∠ACB=180°,
∴∠CAB+2∠CAB=180°,
3∠CAB=180°
∴∠CAB=60°.
5.
45°【解答】由题意知,∠AOB=90°,且A,B,P均位于⊙O的上,所以有∠APB=∠AOB=45°.
6.
40°【解答】设AB与CD交于点E,
∵AB⊥CD,
∴∠AED=∠CEB=90°,
∵圆心角∠AOC=130°,
∴∠ADC=∠ABC=65°,
∴∠BAD=∠DCB=90°-65°=25°,
∵∠ADC=∠P+∠DCP,
∴∠P=65°-25°=40°.
7.
8【解答】∵OE⊥AP于E,OF⊥PB于F,
∴AE=PE,PF=BF,
∴EF是△APB的中位线,
∴EF∥AB,EF=AB=8;
8.
57°【解答】∵在△ABF和△ADE中
∠A+∠ABF+∠F=180°,∠A+∠E+∠ADE=180°,
∴∠A+∠ABF+∠F+∠A+∠E+∠ADE=180°+180°=360°,
∵∠ADE+∠ABF=180°,
∴2∠A+∠E+∠F=180°,
∴2∠A=180°-36°-30°=114°,
∴∠A=57°.
9.【解答】四边形EBCM是菱形,
理由:∵BM平分∠ABC交外接圆于点M,∴∠EBM=∠CBM=∠ABC,
∵∠ABC=2∠A,∴∠A=∠ABM=∠CBM,
∵∠A=∠BMC,∴∠ABM=∠BMC=∠CBM,∴BE∥CM,BC=CM,
∵ME∥BC,∴四边形EBCM是菱形.
10.
【解答】(1)连接OB、OC;
∵△ABC是⊙O的内接正三角形,
∴OB=OC,∠BOC=120°,∠OBC=∠OCB=∠OBA=30°,
在△OBM和△OCN中,OB=OC,∠OBM=∠OCN,BM=CN,
∴△OBM≌△OCN(SAS),
∴∠MOB=∠NOC,
∴∠MON=∠BOC=120°;
(2)同理在图②中可求得∠MON=∠BOC=90°,
在图③中可求得∠MON=∠BOC==72°,
∴在n边形图中,∠MON=∠BOC=.
五、优化提高
1.
118°
【解答】如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=124°,
∴∠ADB=∠AOB=×124°=62°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°-62°=118°.
2.
(12,0)
【解答】设线段BA的中点为E,
∵点A(0,4),B(0,-6),
∴AB=10,E(0,-1).
如图所示,过点E在第四象限作EP⊥BA,且EP=AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5,
由勾股定理得:CF==7,
∴OC=OF+CF=5+7=12,
∴点C坐标为(12,0).
3.【解答】(1)证明:连结AC,延长PO交AC于H,如图1,
∵P是弧ABC的中点,∴PH⊥AC,
∵AB是⊙O的直径,∴∠ACB=90°,
∴BC⊥AC,∴OP∥BC.
(2)如图2,
∵P是弧AC的中点,∴PA=PC,∴∠PAC=∠PCA,
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO,
当DO=DC,设∠DCO=x,则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x,
∵∠OPA=∠PAO=x,∴∠POD=2x,
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°,
当CO=CD,设∠DCO=x,则∠OPC=x,∠PAO=x,
∴∠POD=2x,∴∠ODC=∠POD+∠OPC=3x,
∵CD=CO,∴∠DOC=∠ODC=3x,
在△POC中,x+x+5x=180°,解得x=()°,即∠PAO=()°.
综上所述,∠A的度数为36°或()°.
4.【解答】证明:连结OM,ON,OA,OD,
∵=,∴=,∴AB=CD,
∵点M、N分别是AB、CD的中点,
∴∠OMA=∠OMP=90°,∠OND=∠ONP=90°,AM=AB,DN=CD,
∴AM=DN,
∵OA=OD,
在Rt△OMA和Rt△OND中,OM=,ON=,
∴OM=ON,∴∠OMN=∠ONM,∴∠PMN=∠PNM,∴PM=PN,∴△PMN是等腰三角形.
5.【解答】证明:∵∠APB=∠AOB,又∠AOB=,
∴即圆周角的度数等于其所对的弧的度数的一半.
(1)连BC,则∠APC=∠PCB+∠PBC
∠PCB的度数等于弧BD的度数的一半,∠PBC的度数等于弧AC的度数的一半,
∠APC=(+);
(2)问题(1)中的结论不成立.
类似的结论为:∠BPC=(-).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第8讲、圆心角与圆周角
一、课前检测
(一)选择题(共4小题)
1.
若和的度数相等,则下列命题中,正确的是(
)
A.=
B.与的长度相等
C.所对的弦和所对的弦相等
D.所对的圆心角与所对的圆心角相等
2.
如图,点O是两个同心圆的圆心,大圆的半径OA,OB分别交小圆于点C,D.下列结论中正确的个数有( )
①∠OCD=∠OAB;
②AB=CD;
③=
A.0个
B.1个
C.2个
D.3个
3.
如图,A,D是⊙O上的两点,BC是直径.若∠D=35°,则∠OCA的度数是( )
A.35°
B.55°
C.65°
D.70°
第3题
第4题
4.
如图,∠1,∠2,∠3,∠4的大小关系是(
)
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
(二)填空题(共2小题)
5.
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为______.
第5题
第6题
6.
如图,点A,B,C在⊙O上,延长CO交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为_______.
(三)解答题(共1小题)
7.如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断和是否相等,并说明理由.
二、考点梳理
考点一:圆心角
顶点在圆心的角叫做圆心角.1°圆心角所对的弧叫做1°的弧,n°的圆心角所对的弧就是n°的弧.
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
重要提示:在使用圆心角定理时,一定要注意“在同圆或等圆中”这一前提.
1.证明圆的两条弦相等时,常考虑证两条弦所对的圆心角相等,也考虑利用全等三角形、等角对等边、三线合一以及两条线段都等于第三条线段等方法来证.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
考点二:圆周角
顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
圆周角的两个特征:(1)角的顶点在圆上;(2)角的两边都与圆相交.
在同圆或等圆中,同弧或等弧所对的圆周角相等(都等于该弧所对的圆心角的一半);相等的圆周角所对的弧也相等.
三、重点突破
重点一:圆心角
例1.已知⊙O的半径为5cm,弦AB的长为5cm,则弦AB所对的圆周角的度数是_______.
(点拨:根据题意画出图形,有两个角)
例2.如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,求的度数.
(点拨:连结CD)
例3.
如图,已知AB,CD是⊙O的两条直径,BE是⊙O的弦,且BE∥CD.求证:=
.
(点拨:需推知∠AOC=∠COE即可)
例4.
如图所示,△ABC为等边三角形,BC为⊙O的直径,⊙O分别与AB、AC相交于D、E.
求证:(1)==.
(2)AD=DB,AE=EC.
例5.如图,已知AB是⊙O的直径,M,N分别是OA,OB的中点,CM⊥AB,DN⊥AB.求证:=.
(点拨:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等)
重点二:圆周角
例1.已知:如图,BC为⊙O的直径,BF为弦,A为的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
(点拨:垂径定理,直角三角形的性质以及弧、弦的关系)
例2.如图,△ABC是⊙O的内接三角形,C是优弧AB上的一点(点C不与点A,B重合).设∠OAB=α,∠C=β.
(1)当α=36°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
例3.如图,在△ABC中,AB=AC,∠BAC=40°.以AB为直径的半圆分别交AC,BC于点E,D,求,及的度数.
(点拨:在同圆或等圆中,圆周角的度数等于它所夹弧所对的圆心角度数的一半)
例4.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
(点拨:圆周角定理)
例5.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,,∠APC=∠CPB=60°.
(1)判断△ABC的形状;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
(点拨:在PC上截取PD=AP)
四、经典练习
A组
(一)选择题(共3小题)
1.
已知,是同圆中的两段弧,且=2,则弦AB与CD的关系是(
)
A.AB=2CD
B.AB<2CD
C.AB>2CD
D.不能确定
2.
已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧的中点,若△POC为直角三角形,则PB的长度( )
A.1
B.5
C.1或5
D.2或4
3.
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为(
)
A.cm
B.3cm
C.cm
D.9cm
(二)
填空题(共4小题)
4.
如图,△ABC是⊙O的内接三角形,∠B=40°,点P在劣弧AC上移动(点P与点A、C不重合),则∠α的变化范围是________.
第4题
第5题
5.
如图,游乐园的大观览车半径为25米,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟,某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是_________米(观览处最低处距地面的高度忽略不计).
6.
如果一条弦将圆分成两段弧,它们的度数之比为3:1,那么此弦的弦心距的长度与与此弦的长度的比为_________.
7.
圆的一条弦把圆分成5:1两部分,如果圆的半径是2cm,那么这条弦的长是______cm.
(三)解答题(共3小题)
8.
如图,已知△ABC内接于⊙O,点A,B,C把⊙O三等分.
(1)试判断△ABC的形状,并说明理由;
(2)求∠AOB的度数.
9.
如图,在⊙O中半径OA⊥OB,C,D是弧AB的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.
10.
如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F是AC上的一点,AB=AD,∠BFC=∠BAD=2∠DFC.求证:
(1)CD⊥DF;
(2)BC=2CD.
B组
(一)选择题(共4小题)
1.如图,在菱形ABCD中,AC=AB,以顶点B为圆心,以AB长为半径画圆,延长DC交⊙B于点E,则的度数为( )
A.120°
B.90°
C.60°
D.30°
第1题
第3题
第4题
2.若⊙O内的一条弦与直径相交成30°的角,并把直径分成2cm和6cm两段,则这条弦的弦心距为(
)
A.1cm
B.2cm
C.3cm
D.4cm
3.
如图,AB为⊙O的直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P(
)
到CD的距离保持不变
B.位置不变
C.等分
D.随点C的移动而移动
4.
如图,△ABC是⊙O的内接三角形,且AB≠AC,∠ABC和∠ACB的平分线分别交⊙O于点D,E,且BD=CE,则∠A等于( )
A.90°
B.60°
C.45°
D.30°
(二)填空题(共4小题)
5.
如图,用四个边长为1的小正方形拼成一个大正方形,A,B,O是小正方形的顶点,⊙O的半径为1,P是⊙O上的点,且位于右上方的小正方形内,则∠APB的度数为_______.
第5题
第6题
6.
如图,AB,CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD,CB的延长线相交于点P,则∠P的度数为________.
7.
如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
第7题
第8题
8.
如图,A、B、C、D为⊙O上四点,AB、DC交于E点,AD、BC交于点F.若∠E=36°,∠F=30°,则∠A的度数为________.
(三)解答题(共3小题)
9.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB于点E.试判断四边形EBCM的形状,并加以证明.
10.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM、ON,求∠MON的度数.
(2)图②、③、…④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、…正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是_______,图③中∠MON的度数是_______;…由此可猜测在n边形图中∠MON的度数是_______.
五、优化提高
1.
如图,扇形OAB的圆心角为124°,C是弧上一点,则∠ACB=______.
2.
已知:点A(0,4),B(0,-6),C为x轴正半轴上一点,且满足∠ACB=45°,则点C坐标为________.
3.
已知AB是⊙O的直径,C是圆周上的动点,P是的中点.
(1)如图1,求证:OP∥BC;
(2)如图2,PC交AB于D,当△ODC是等腰三角形时,求∠A的度数.
4.
已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,=,求证:△PMN是等腰三角形.
5.
我们把1°的圆心角所对的弧叫做1°的弧.则圆心角AOB的度数等于它所对的弧AB的度数记为:∠AOB=.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图1给予证明(不要求写己知、求证.只需直接证明),并解决以下的问题(1)和问题(2).
问题(1):如图2,⊙0的两条弦AB、CD相交于圆内一点P,求证:∠APC=(+);
问题(2):如图3,⊙0的两条弦AB、CD相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明)
参考答案
一、课前检测
1.
D
2.
B【解答】①∵OC=OD,OA=OB,
∴∠OCD=,∠OAB=,
∴∠OCD=∠OAB,故①正确;
②∵CD<AB,故②错误;
③∵与不是等圆或同圆中的弧,
∴≠,故③错误.
3.
B【解答】∵∠AOC=2∠D,∠D=35°,
∴∠AOC=2∠D=2×35°=70°,
在等腰△OAC中,∵OA=OC,∠AOC=70°,
∴∠OCA==55°.
4.
B【解答】如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,
根据三角形的外角的性质得:∠5>∠4,∠2>∠6,
∴∠4<∠1=∠3<∠2.
5.
50°【解答】连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴的度数为50°.
6.
110°【解答】∵∠A=50°,
∴∠BOC=2∠A=100°,
∵∠B=30°,∠BOC=∠B+∠BDC,
∴∠BDC=∠BOC-∠B=100°-30°=70°,
∴∠ADC=180°-∠BDC=110°.
7.【解答】=,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴=.
三、重点突破
重点一:圆心角
例1.
30°或150°
【解答】如图:在优弧AB上取点C,连接AC,BC,在劣弧上取点D,连接AD,BD,
∵⊙O的半径为5cm,弦AB的长为5cm,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠C=∠AOB=30°,
∴∠D=180°-∠C=150°.
∴弦AB所对的圆周角的度数是:30°或150°.
例2.
52°【解答】连结CD,如图,
∵∠C=90°,∠A=26°,
∴∠B=64°,
∵CB=CD,
∴∠CDB=∠B=64°,
∴∠BCD=180°-64°-64°=52°,
∴的度数为52°.
例3.【解答】证明:连接OE,
∵BE∥CD,
∴∠COE=∠E,∠BOD=∠B,
∵OB=OE,
∴∠B=∠E,
∴∠COE=∠BOD,
∵∠AOC=∠BOD,
∴∠AOC=∠COE,
∴=
.
例4.【解答】(1)如图所示,连接OD,OE,
∵OB=OD=OE=OC,∠B=∠C=60°
∴△BOD与△COE都是等边三角形
∴∠BOD=∠COE=60°
∠DOE=180°-∠BOD-∠COE=60°
∴∠DOE=∠BOD=∠COE
∴==.
(2)连接BE,CD,
∵∠BOD=∠COE=60°
∴∠BCD=30°,∠EBC=30°,
∴DC平分∠ACB,BE平分∠ABC,
∴AD=DB,AE=EC.
例5.【解答】证明:连结OC、OD,如图,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°,
在Rt△OMC和Rt△OND中,OM=ON,OC=OD,
∴Rt△OMC≌Rt△OND(HL),
∴∠COM=∠DON,
∴=.
重点二:圆周角
例1.【解答】证明:连AF,AB,AC.
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠BAD=∠C,
∵∠C=∠F,
∴∠BAD=∠F,
∵A为的中点,
∴∠ABF=∠F,
∴∠BAD=∠ABF,
∴BE=AE.
例2.【解答】(1)连OB,则OA=OB,
∴∠OBA=∠OAB=36°
∴∠AOB=180°-∠OAB-∠OBA=108°
∴β=∠C=∠AOB=54°;
(2)α与β之间关系是α+β=90°.
证明:连OB,则OA=OB,
∴∠OBA=∠OAB=α
∴∠AOB=180°-2α
∴β=∠C=∠AOB=(180°-2α)=90°-α.
∴α+β=90°.
例3.【解答】连接BE、AD,
∵AB是圆的直径,
∴∠ADB=∠AEB=90°,
∴∠ABE=90°-40°=50°,
AD⊥BC,
∵AB=AC,∠BAC=40°,
∴∠BAD=∠DAC=∠BAC=20°,
∴由圆周角定理得:弧BD所对的圆心角的度数是2∠DAB=40°,
弧DE所对的圆心角的度数是2∠DAE=40°,
弧AE的度数是180°-40°-40°=100°
例4.【解答】(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2.
例5.【解答】(1)△ABC是等边三角形.
证明如下:在⊙O中
∵∠BAC与∠CPB是弧BC所对的圆周角,∠ABC与∠APC是弧AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;故答案为:等边三角形;
(2)在PC上截取PD=AP,如图,
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,∠APB=∠ADC,∠ABP=∠ACD,AP=AD,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP
四、经典练习
A组
1.
B【解答】取的中点E,连接AE、BE,
∴弧AE=弧BE,
∵=2,
∴∠AOB=2∠COD,
∴弧AE=弧BE=弧CD,
∵AE+BE>AB,
∴2CD>AB,
∴AB<2CD.
2.
C【解答】∵点C是劣弧的中点,
∴OC垂直平分AB,
∴DA=DB=3,
∴OD==1,
若△POC为直角三角形,只能是∠OPC=90°,
则△POD∽△CPD,
∴,
∴PD2=4×1=4,
∴PD=2,
∴PB=3-2=1,
根据对称性得,
当P在OC的左侧时,PB=3+2=5,
∴PB的长度为1或5.
3.
B
【解答】∵∠CDB=30°,
∴∠COB=30°×2=60°.
又∵⊙O的半径为cm,
∴CE=sin60°=×=,
∴CD=×2=3(cm).
4.
0°<α<80°【解答】∵点P在劣弧
AC上移动,
∴当点P与点C重合时,α最小值=0°;
而∠AOC=2∠B=80°(同弧所对的圆周角是所对的圆心角的一半),
当点P与点A重合时,α最大值=∠AOC=80°,
∵点P不与点A、C重合,
∴α的变化范围是0°<α<80°.
5.
【解答】根据题意,可知:此人运动到了圆的三等分点处,设为点B,则∠AOB=120°,
作BC⊥AD于C,OE⊥BC于E,则CE=OA=25m,
在Rt△BOE中,根据30°所对的直角边是斜边的一半,得BE=m,
则此人距地面AD的高度是米.
6.
1:2
7.2【解答】连接OA,OB,过O作OD⊥AB.
∵一条弦把圆分成5:1两部分,
∴∠AOB=60°,
∴∠2=∠1=30°;
又∵OD⊥AB,OA=2cm,
∴AD=OA=1cm,
∴AB=2AD=2cm.
8.【解答】(1)△ABC为等边三角形;
∵△ABC内接于圆O,点A,B,C把圆O的周长三等分,
∴弧AB=弧AC=弧BC,
∴AB=AC=BC,
∴△ABC为等边三角形;
(2)∵弧AB=弧AC=弧BC,
∴∠BOC=∠AOC=∠AOB,
∴∠AOB=360°÷3=120°.
9.
【解答】连接AC、BD,
∵C,D是弧AB的三等分点,
∴AC=CD=BD,∠AOC=∠COD,OA=OC=OD,
在△ACO与△DCO中,
∵OA=OD,∠AOC=∠DOC,OC=OC,
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC,
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD,
∴AE=BF=CD.
10.
【解答】证明:(1)∵AB=AD,
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°-∠BAD)÷2=90°-∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF.
(2)过F作FG⊥BC于点G,
∵∠ACB=∠ADB,
又∵∠BFC=∠BAD,
∴∠FBC=∠ABD=∠ADB=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,∠GFC=∠BAD=∠DFC,
∵在△FGC和△DFC中,∠GFC=∠DFC,FC=FC,∠ACB=∠ACD,
∴△FGC≌△DFC(ASA),
∴CD=GC=BC.
∴BC=2CD.
B组
1.
C【解答】连接OE,
∵四边形ABCD是菱形,∴AB∥CD,AB=BC,
∵AC=AB,∴△ABC是等边三角形,
∴∠ABC=60°,∴∠BCE=∠ABC=60°,
∵BE=BC,
∴△BCE是等边三角形,∴∠EBC=60°,
∴的度数为60°.
2.
A
【解答】
∵AF=2cm,BF=6cm,∴OF=2cm,
∵∠OEF=90°,∠EFO=30°,
∴OE=1cm,
3.
B【解答】不发生变化.
连接OP,
∵OP=OC,
∴∠P=∠OCP,
∵∠OCP=∠DCP,
∴∠P=∠DCP,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB,
∴弧AP=弧BP,
∴点P为弧AB的中点不变.
4.
B【解答】连接AD、BE,
∵BD=CE
∴弧BD=弧CE,∴∠BAD=∠EBC,
∵∠BAD=∠CAD+∠CAB,∠EBC=∠ABE+∠ABD+∠CBD,
∴∠CAD+∠CAB=∠ABE+∠ABD+∠CBD,
∵∠CAD=∠CBD(同圆中,同弧所对的圆周角相等),
∴∠CAB=∠ABD+∠ABE,
∵∠ABE=∠ACE(同圆中,同弧所对的圆周角相等),
∴∠CAB=∠ABD+∠ACE(等量代换)
∵BD、CE分别平分∠ABC、∠ACB,
∴∠ABD=∠ABC,∠ACE=∠ACB
∴∠CAB=(∠ABC+∠ACB),∴∠ABC+∠ACB=2∠CAB
∵∠CAB+∠ABC+∠ACB=180°,
∴∠CAB+2∠CAB=180°,
3∠CAB=180°
∴∠CAB=60°.
5.
45°【解答】由题意知,∠AOB=90°,且A,B,P均位于⊙O的上,所以有∠APB=∠AOB=45°.
6.
40°【解答】设AB与CD交于点E,
∵AB⊥CD,
∴∠AED=∠CEB=90°,
∵圆心角∠AOC=130°,
∴∠ADC=∠ABC=65°,
∴∠BAD=∠DCB=90°-65°=25°,
∵∠ADC=∠P+∠DCP,
∴∠P=65°-25°=40°.
7.
8【解答】∵OE⊥AP于E,OF⊥PB于F,
∴AE=PE,PF=BF,
∴EF是△APB的中位线,
∴EF∥AB,EF=AB=8;
8.
57°【解答】∵在△ABF和△ADE中
∠A+∠ABF+∠F=180°,∠A+∠E+∠ADE=180°,
∴∠A+∠ABF+∠F+∠A+∠E+∠ADE=180°+180°=360°,
∵∠ADE+∠ABF=180°,
∴2∠A+∠E+∠F=180°,
∴2∠A=180°-36°-30°=114°,
∴∠A=57°.
9.【解答】四边形EBCM是菱形,
理由:∵BM平分∠ABC交外接圆于点M,∴∠EBM=∠CBM=∠ABC,
∵∠ABC=2∠A,∴∠A=∠ABM=∠CBM,
∵∠A=∠BMC,∴∠ABM=∠BMC=∠CBM,∴BE∥CM,BC=CM,
∵ME∥BC,∴四边形EBCM是菱形.
10.
【解答】(1)连接OB、OC;
∵△ABC是⊙O的内接正三角形,
∴OB=OC,∠BOC=120°,∠OBC=∠OCB=∠OBA=30°,
在△OBM和△OCN中,OB=OC,∠OBM=∠OCN,BM=CN,
∴△OBM≌△OCN(SAS),
∴∠MOB=∠NOC,
∴∠MON=∠BOC=120°;
(2)同理在图②中可求得∠MON=∠BOC=90°,
在图③中可求得∠MON=∠BOC==72°,
∴在n边形图中,∠MON=∠BOC=.
五、优化提高
1.
118°
【解答】如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=124°,
∴∠ADB=∠AOB=×124°=62°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°-62°=118°.
2.
(12,0)
【解答】设线段BA的中点为E,
∵点A(0,4),B(0,-6),
∴AB=10,E(0,-1).
如图所示,过点E在第四象限作EP⊥BA,且EP=AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5,
由勾股定理得:CF==7,
∴OC=OF+CF=5+7=12,
∴点C坐标为(12,0).
3.【解答】(1)证明:连结AC,延长PO交AC于H,如图1,
∵P是弧ABC的中点,∴PH⊥AC,
∵AB是⊙O的直径,∴∠ACB=90°,
∴BC⊥AC,∴OP∥BC.
(2)如图2,
∵P是弧AC的中点,∴PA=PC,∴∠PAC=∠PCA,
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO,
当DO=DC,设∠DCO=x,则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x,
∵∠OPA=∠PAO=x,∴∠POD=2x,
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°,
当CO=CD,设∠DCO=x,则∠OPC=x,∠PAO=x,
∴∠POD=2x,∴∠ODC=∠POD+∠OPC=3x,
∵CD=CO,∴∠DOC=∠ODC=3x,
在△POC中,x+x+5x=180°,解得x=()°,即∠PAO=()°.
综上所述,∠A的度数为36°或()°.
4.【解答】证明:连结OM,ON,OA,OD,
∵=,∴=,∴AB=CD,
∵点M、N分别是AB、CD的中点,
∴∠OMA=∠OMP=90°,∠OND=∠ONP=90°,AM=AB,DN=CD,
∴AM=DN,
∵OA=OD,
在Rt△OMA和Rt△OND中,OM=,ON=,
∴OM=ON,∴∠OMN=∠ONM,∴∠PMN=∠PNM,∴PM=PN,∴△PMN是等腰三角形.
5.【解答】证明:∵∠APB=∠AOB,又∠AOB=,
∴即圆周角的度数等于其所对的弧的度数的一半.
(1)连BC,则∠APC=∠PCB+∠PBC
∠PCB的度数等于弧BD的度数的一半,∠PBC的度数等于弧AC的度数的一半,
∠APC=(+);
(2)问题(1)中的结论不成立.
类似的结论为:∠BPC=(-).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
