第一章三角形的初步知识-浙教版八年级数学上册综合测试(Word版 含解析)
文档属性
| 名称 | 第一章三角形的初步知识-浙教版八年级数学上册综合测试(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览


文档简介
八年级上册第一章
三角形的初步知识综合测试
一.选择题
1.
下列各组数不可能是一个三角形的边长的是(
)
A.
5,12,13
B.
5,7,12
C.
5,7,7
D.
4,6,9
2.
三角形的一个外角是锐角,则此三角形的形状是( )
A.
锐角三角形
B.
钝角三角形
C.
直角三角形
D.
无法确定
3.
有下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是( )
A.
①②③
B.
①②
C.
②③④
D.
①③④
4.
已知△DEF≌△ABC,AB=AC,且△ABC的周长是23cm,BC=4cm,则△DEF的边长中必有一边等于( )
A.
9.5cm
B.
9.5cm或9cm
C.
9cm
D.
4cm或9cm
5.
点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.
∠APC>∠B
B.
∠APC=∠B
C.
∠APC<∠B
D.
不能确定
6.
到△ABC的三条边距离相等的点是△ABC的( )
A.
三条中线的交点
B.
三条内角平分线的交点
C.
三条高所在直线的交点
D.
三条垂直平分线的交点
7.
用9根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余重叠和折断,则能摆出不同的三角形的个数是(
)
A.
1个
B.
2个
C.
3个
D.
4个
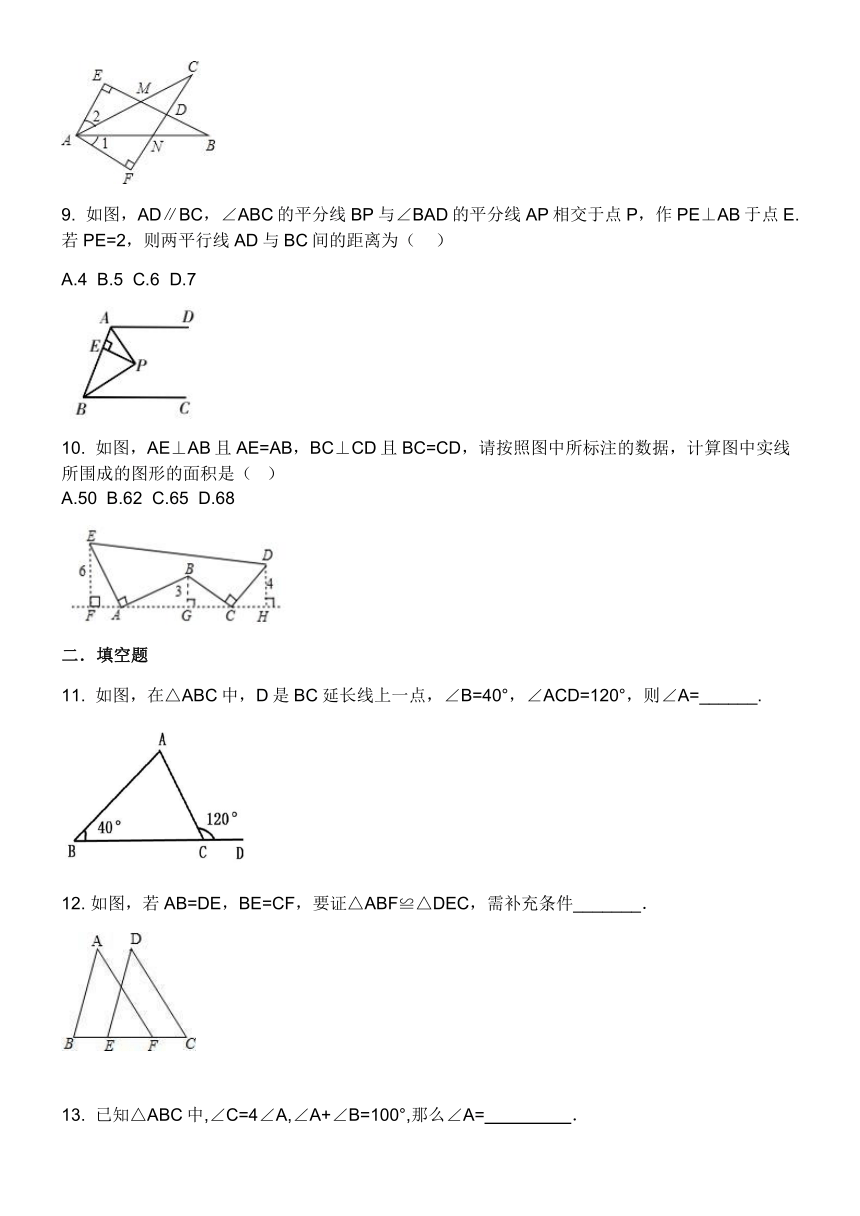
8.如图EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(
).
A.4个
B.3个
C.2个
D.1个
9.
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(
)
A.4
B.5
C.6
D.7
10.
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积是(???)
A.50
B.62
C.65
D.68
二.填空题
11.
如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A=______.
12.
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件_______.
13.
已知△ABC中,∠C=4∠A,∠A+∠B=100°,那么∠A=
.
14.
已知三角形三边长分别是1、x、2,且x为整数,那么x的值是
__________.
15.
当三角形中一个内角a是另一个内角β
的两倍时,我们称此三角形为“特征三角形”,其中a称为“特征角”如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为
____.
16.
如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,直线BE交AC于点F,若△ABC的面积为24,则△AEF的面积为____.
三.解答题
17.
填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF
求证:(1)∠C=∠F;
??????????(2)AC//DF
证明:(1)∵BC//EF(已知)
????∴∠ABC
=?_____
(?_____)
????∵AD
=
BE
????∴AD
+
DB
=
DB
+
BE
即?_____
=
DE
??在△ABC与△DEF中
???????
?????∴△ABC
≌
△DEF(?_____)
???∴∠C
=
∠F(?_____)
(2)∵△ABC
≌
△DEF
????∴∠A
=
∠FDE(?_____)
????∴AC//DF(?_____)
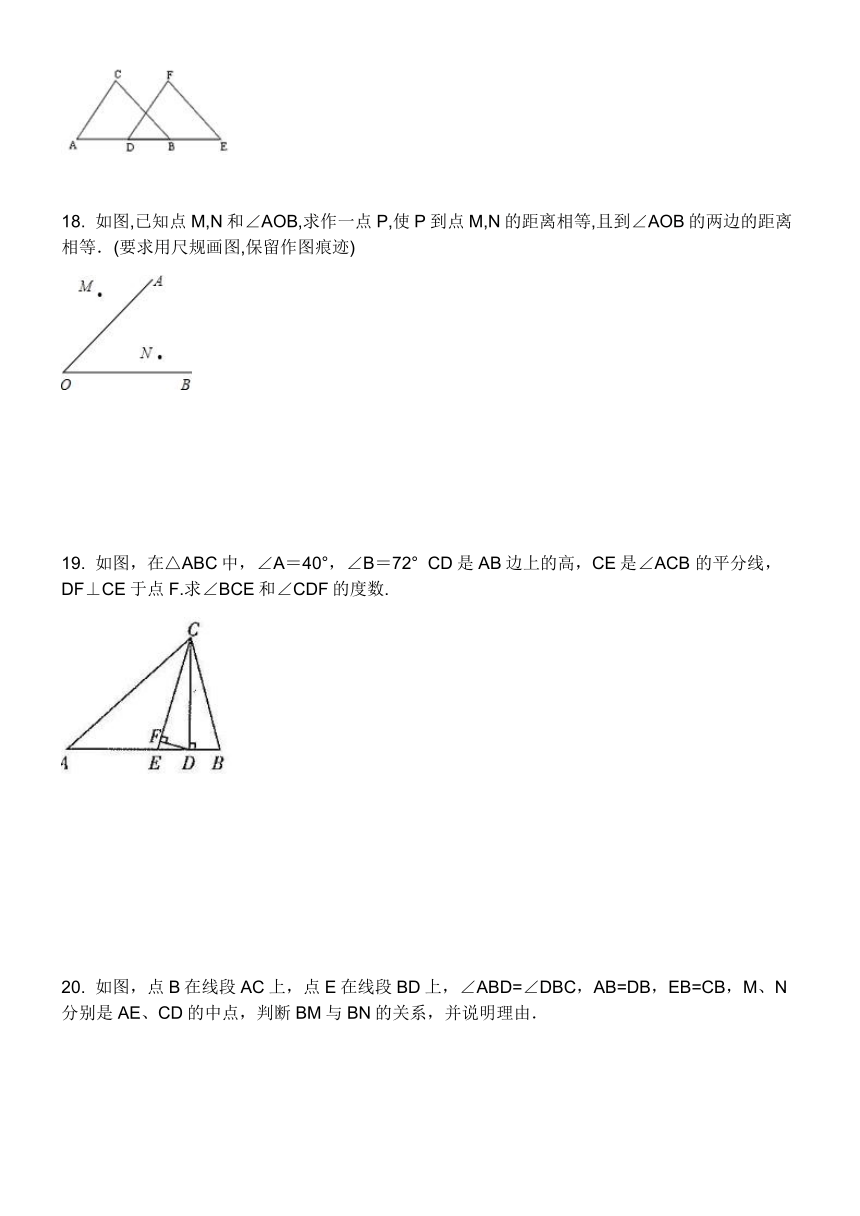
18.
如图,已知点M,N和∠AOB,求作一点P,使P到点M,N的距离相等,且到∠AOB的两边的距离相等.(要求用尺规画图,保留作图痕迹)
19.
如图,在△ABC中,∠A=40°,∠B=72°
?CD是AB边上的高,CE是∠ACB
的平分线,DF⊥CE于点F.求∠BCE和∠CDF的度数.
20.
如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
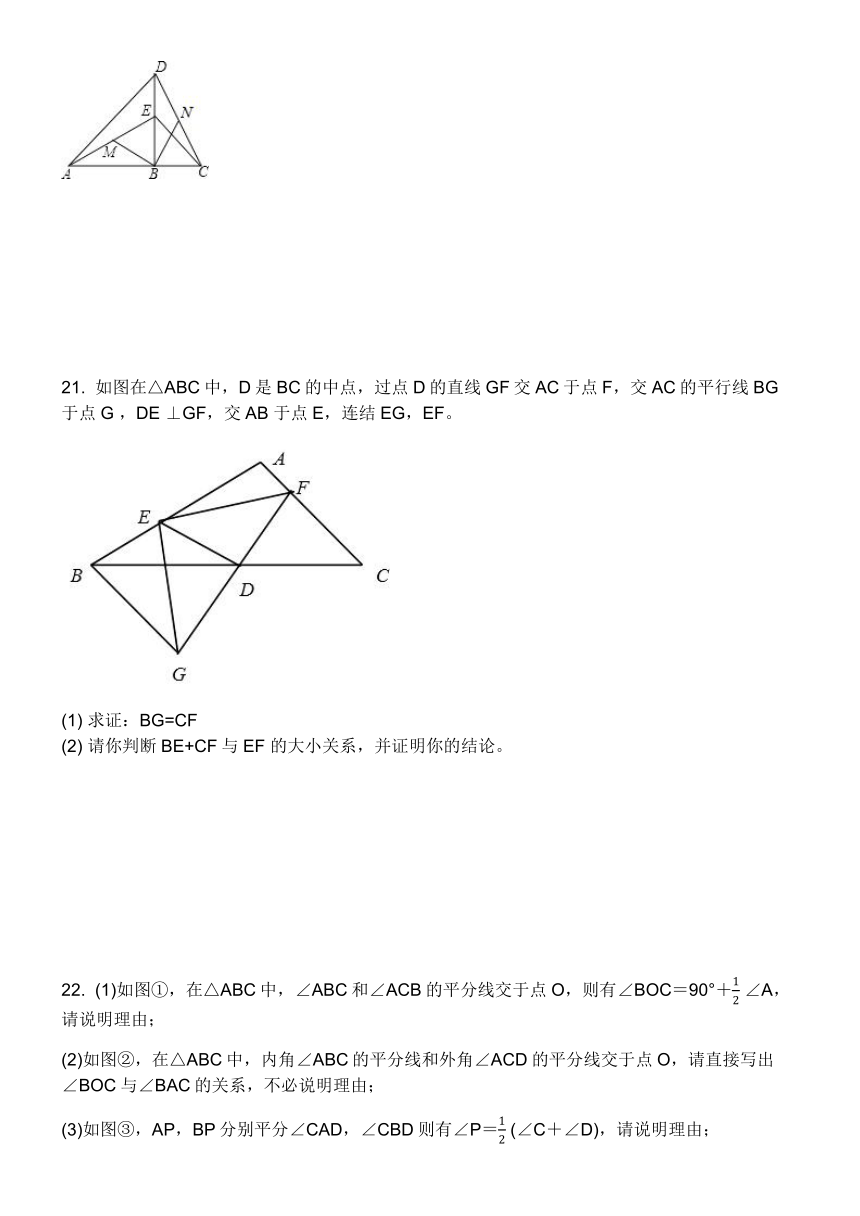
21.
如图在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G
,DE
⊥GF,交AB
于点E,连结EG,EF。
(1)
求证:BG=CF
(2)
请你判断BE+CF与EF
的大小关系,并证明你的结论。
(1)如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,则有∠BOC=90°+
∠A,请说明理由;
如图②,在△ABC中,内角∠ABC的平分线和外角∠ACD的平分线交于点O,请直接写出∠BOC与∠BAC的关系,不必说明理由;
如图③,AP,BP分别平分∠CAD,∠CBD则有∠P=
(∠C+∠D),请说明理由;
(4)如图④,AP,BP分别平分∠CAM,∠CBD,请直接写出∠P与∠C、∠D的关系,不必说明理由.
参考答案
1.
--------------------------------------------------------------------------
B
【解答】解:A、5+12>13,能构成三角形;
B、5+7=12,不能构成三角形;
C、5+7>7,能构成三角形;
D、4+6>9,能构成三角形.
故选B.
【分析】看哪个选项中两条较小的边的和小于最大的边即可.
2.
--------------------------------------------------------------------------
B
三角形的一个外角是锐角,根据邻补角的定义可得它相邻的内角为钝角,即可判断三角形的形状是钝角三角形.
解:∵三角形的一个外角是锐角,
∴与它相邻的内角为钝角,
∴三角形的形状是钝角三角形.
故选B.
3.
--------------------------------------------------------------------------
【分析】根据全等三角形的判定的知识判断.
【解答】解:①是边边边(SSS);
②是两边夹一角(SAS);
③两角夹一边(ASA)都成立.
根据三角形全等的判定,都可以确定唯一的三角形;
而④则不能.
故选A.
4.
--------------------------------------------------------------------------
A
根据等腰三角形的性质求出AB,再根据全等三角形对应边相等解答.
解:∵BC=4cm,
∴腰长AB=
×(23-4)=9.5cm,
∵△DEF≌△ABC,
∴△DEF的边长中必有一边等于9.5cm.
故选A.
5.
--------------------------------------------------------------------------
【解答】解:如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A.
【分析】作出图形,延长AP与BC相交于点D,然后根据三角形的一个外角大于任何一个与它不相邻的内角解答.
6.
--------------------------------------------------------------------------
B
7.
--------------------------------------------------------------------------
【答案】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.根据三角形的三边关系,可以首先确定一边,再加以分析.
有2,3,4;3,3,3;4,4,1三种情况.
故选C.
8.
--------------------------------------------------------------------------
B【解答】解:∵∠B+∠BAE=90°,∠C+∠CAF=90°,∠B=∠C
∴∠1=∠2(①正确)
∵∠E=∠F=90°,∠B=∠C,AE=AF
∴△ABE≌△ACF(ASA)
∴AB=AC,BE=CF(②正确)
∵∠CAN=∠BAM,∠B=∠C,AB=AC
∴△ACN≌△ABM(③正确)
∴CN=BM(④不正确).
所以正确结论有①②③.
故答案为B.
【分析】由已知条件,可直接得到三角形全等,得到结论,采用排除法,对各个选项进行验证从而确定正确的结论.
9.
--------------------------------------------------------------------------
答案:A.
解:过点P作MN⊥AD,交AD于M点,交BC于N点.
∵AD∥BC,MN⊥AD,
∴PN⊥BC.
∵PN⊥BC,PE⊥AB,PM⊥AD,BP为∠ABC的平分线,AP为∠BAD的平分线且相交于点P,
∴PM=PE=2,PE=PN=2.
∴MN=2+2=4,即两平行线AD与BC间的距离为4.
故选A.
【考点提示】
本题主要考查的是角平分线的性质,熟练掌握角平分线的性质是解题的关键;
【解题方法提示】
过点P作MN⊥AD,交AD于M点,交BC于N点,首先证明PN⊥BC,然后依据角平分线的性质可得到PM=PE=2,PE=PN=2;
最后,依据MN=PM+PN求解即可,赶快动手试试吧!
10.
--------------------------------------------------------------------------
A.
试题解析:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°?∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△ABG
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=(6+4)×16-3×4-6×3=50.
故选A.
考点:1.全等三角形的判定与性质,2.勾股定理
11.
--------------------------------------------------------------------------
解析根据题意知,本题可以直接根据三角形的外角性质,即三角形的外角等于不相邻的两内角之和,进行计算.
答案解:根据三角形的外角性质得∠A=∠ACD-∠B=120°-40°=80°.
故答案为:80°
点评根据本题题干及题意可知,这是一道考查三角形外角性质的题,牢牢掌握三角形的外角等于不相邻的两内角之和是解题的关键,这样可以提高解题的速度和准确率.
12.
--------------------------------------------------------------------------
【解答】解:可补充AF=CD或∠B=∠DEC;
当AF=CD时,三条边对应相等,所以两三角形全等;
当∠B=∠DEC时,两边夹一角,也全等.
故填AF=CD或∠B=∠DEC.
【分析】要使△ABF≌△DEC,已知AB=ED,EB=∠CF,具备了两组边对应相等,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.
13.
--------------------------------------------------------------------------
解:∵∠A+∠B+∠C=180°,∠C=4∠A,
∴∠A+∠B+4∠A=180°,
∵∠A+∠B=100°,
∴∠B=100°-∠A,
∴∠A+∠100°-∠A+4∠A=180°,
∴∠A=20°,
故答案为20°.
根据三角形内角和定理计算即可.
14.
--------------------------------------------------------------------------
2
【解答】解:∵三角形的三边长分别为1,x,2,
∴第三边的取值范围为:1<x<3
∵x为整数,
∴x=2.
故答案为:2.
【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,求解即可.
15.
--------------------------------------------------------------------------
解:由题意得:α=2β,α=100°,则β=50°,
180°-100°-50°=30°,
故答案为:30°.
此题考查了三角形内角和定理.解答此题时就是先根据已知一个内角α是另一个内角β的两倍得出β的度数,再根据三角形的内角和进而求出最小内角即可.
16.
--------------------------------------------------------------------------
解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
∵△ABC的面积为24,BD=CD,
∴S△ABD=S△ACD=×S△ABC=12,
又∵E是AD中点,
∴S△ABE=S△BDE=×S△ABD=6,
在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=CD,
∴S△BCF=4y,
则有,
解得,
则△AEF的面积为2.
故答案为:2.
先过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,由于△ABC的面积为24,BD=CD,可求S△ABD,S△ACD,又因为E是AD中点,可求S△ABE.在△ADG中,DG∥BF,E是AD中点,利用平行线分线段成比例定理的推论,可知AF=FG,从而可知△AEF∽△ADG,再利用相似三角形的面积比等于相似比的平方,可得∴S△ADG=4x,同理可求S△BCF=4y,再利用三角形面积之间的加减关系可得关于x、y的二元一次方程,求解即可.
17.
--------------------------------------------------------------------------
1)∠E(或∠DEF);两直线平行,同位角相等;
AB;已知;SAS(或边角边);全等三角形的对应角
(2)全等三角形的对应角;同错角相等,两直线平行;
18.
--------------------------------------------------------------------------
解:如图所示,点P就是所求的点.
使P到点M,N的距离相等,即画MN的垂直平分线,且到∠AOB的两边的距离相等,即画它的角平分线,两线的交点就是点P的位置.
19.
--------------------------------------------------------------------------
解:根据三角形内角和定理可得出
∠ACB=180°-40°-72°=68°,∵CE是∠ACB的平分线,∴∠BCE=34°;
∵CE是∠ACB的平分线,
∴∠BCE=34°,
∴∠BCD=180°-72°-90°=18°,
∴∠ECD=34°-18°=16°;
∵DF⊥CE,∠ECD=16°,
∴∠CDF=180°-16°-90°=74°.
利用直角三角形内角性质求角的度数
20.
--------------------------------------------------------------------------
解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM=
AE,BN=CN=DN=
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.
【分析】根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM=
AE,BN=CN=DN=
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
21.
--------------------------------------------------------------------------
(1)证明:∵BG//AC,
∴∠BGF=∠CFG,∠DBG=∠DCF,
∵D是BC的中点,
∴BD=CD,
∴△BDG≌△CDF,
∴BG=CF。
(2)解:BE+CF>EF。
证明:由(1)可得△BDG≌△CDF,
∴GD=FD,
又因为DE
⊥GF,
∴∠EDG=∠EDF=90°,
且ED=ED,
∴△EDG≌△EDF,
∴EG=EF,
在△BEG中,BG+BE>EG,
∴BE+CF=BE+BG>EG=EF,
∴BE+CF>EF。
【分析】(1)证明△BDG≌△CDF即可得到BG=CF;
(2)BE+CF与EF的关系,不能直接证明;由(1)可得CF=BG,容易得到BE+CF=BE+BG>EG,从而需要证明EG与EF的关系;由(1)可得GD=DF,即需要证明△EDG≌△EDF,可得到EG=EF。
22.
--------------------------------------------------------------------------
解:(1)∠BOC=180°-(∠1+∠2)又有2(∠1+∠2)=180°-∠A则∠1+∠2=90°-
∠A(2)∠BOC=
∠A(3)①△ADE和△EPB中有∠D+∠DAE=∠P+∠PBE即∠D+
∠DAC=∠P+
∠CBD同理②在△BCF和△PAF中有∠C+
∠CBD=∠P+
∠DAC,①+②就得∠P=
(∠C+∠D)(4)∠P=90°+
(∠C+∠D)故答案为:(1)(3)略(2)∠BOC=
∠A(4)∠P=90°+
(∠C+∠D)
由三角形的角平分线性质找出角的关系,再根据三角形内角和确定各角关系.
三角形的初步知识综合测试
一.选择题
1.
下列各组数不可能是一个三角形的边长的是(
)
A.
5,12,13
B.
5,7,12
C.
5,7,7
D.
4,6,9
2.
三角形的一个外角是锐角,则此三角形的形状是( )
A.
锐角三角形
B.
钝角三角形
C.
直角三角形
D.
无法确定
3.
有下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是( )
A.
①②③
B.
①②
C.
②③④
D.
①③④
4.
已知△DEF≌△ABC,AB=AC,且△ABC的周长是23cm,BC=4cm,则△DEF的边长中必有一边等于( )
A.
9.5cm
B.
9.5cm或9cm
C.
9cm
D.
4cm或9cm
5.
点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.
∠APC>∠B
B.
∠APC=∠B
C.
∠APC<∠B
D.
不能确定
6.
到△ABC的三条边距离相等的点是△ABC的( )
A.
三条中线的交点
B.
三条内角平分线的交点
C.
三条高所在直线的交点
D.
三条垂直平分线的交点
7.
用9根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余重叠和折断,则能摆出不同的三角形的个数是(
)
A.
1个
B.
2个
C.
3个
D.
4个
8.如图EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(
).
A.4个
B.3个
C.2个
D.1个
9.
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(
)
A.4
B.5
C.6
D.7
10.
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积是(???)
A.50
B.62
C.65
D.68
二.填空题
11.
如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A=______.
12.
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件_______.
13.
已知△ABC中,∠C=4∠A,∠A+∠B=100°,那么∠A=
.
14.
已知三角形三边长分别是1、x、2,且x为整数,那么x的值是
__________.
15.
当三角形中一个内角a是另一个内角β
的两倍时,我们称此三角形为“特征三角形”,其中a称为“特征角”如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为
____.
16.
如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,直线BE交AC于点F,若△ABC的面积为24,则△AEF的面积为____.
三.解答题
17.
填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF
求证:(1)∠C=∠F;
??????????(2)AC//DF
证明:(1)∵BC//EF(已知)
????∴∠ABC
=?_____
(?_____)
????∵AD
=
BE
????∴AD
+
DB
=
DB
+
BE
即?_____
=
DE
??在△ABC与△DEF中
???????
?????∴△ABC
≌
△DEF(?_____)
???∴∠C
=
∠F(?_____)
(2)∵△ABC
≌
△DEF
????∴∠A
=
∠FDE(?_____)
????∴AC//DF(?_____)
18.
如图,已知点M,N和∠AOB,求作一点P,使P到点M,N的距离相等,且到∠AOB的两边的距离相等.(要求用尺规画图,保留作图痕迹)
19.
如图,在△ABC中,∠A=40°,∠B=72°
?CD是AB边上的高,CE是∠ACB
的平分线,DF⊥CE于点F.求∠BCE和∠CDF的度数.
20.
如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
21.
如图在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G
,DE
⊥GF,交AB
于点E,连结EG,EF。
(1)
求证:BG=CF
(2)
请你判断BE+CF与EF
的大小关系,并证明你的结论。
(1)如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,则有∠BOC=90°+
∠A,请说明理由;
如图②,在△ABC中,内角∠ABC的平分线和外角∠ACD的平分线交于点O,请直接写出∠BOC与∠BAC的关系,不必说明理由;
如图③,AP,BP分别平分∠CAD,∠CBD则有∠P=
(∠C+∠D),请说明理由;
(4)如图④,AP,BP分别平分∠CAM,∠CBD,请直接写出∠P与∠C、∠D的关系,不必说明理由.
参考答案
1.
--------------------------------------------------------------------------
B
【解答】解:A、5+12>13,能构成三角形;
B、5+7=12,不能构成三角形;
C、5+7>7,能构成三角形;
D、4+6>9,能构成三角形.
故选B.
【分析】看哪个选项中两条较小的边的和小于最大的边即可.
2.
--------------------------------------------------------------------------
B
三角形的一个外角是锐角,根据邻补角的定义可得它相邻的内角为钝角,即可判断三角形的形状是钝角三角形.
解:∵三角形的一个外角是锐角,
∴与它相邻的内角为钝角,
∴三角形的形状是钝角三角形.
故选B.
3.
--------------------------------------------------------------------------
【分析】根据全等三角形的判定的知识判断.
【解答】解:①是边边边(SSS);
②是两边夹一角(SAS);
③两角夹一边(ASA)都成立.
根据三角形全等的判定,都可以确定唯一的三角形;
而④则不能.
故选A.
4.
--------------------------------------------------------------------------
A
根据等腰三角形的性质求出AB,再根据全等三角形对应边相等解答.
解:∵BC=4cm,
∴腰长AB=
×(23-4)=9.5cm,
∵△DEF≌△ABC,
∴△DEF的边长中必有一边等于9.5cm.
故选A.
5.
--------------------------------------------------------------------------
【解答】解:如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A.
【分析】作出图形,延长AP与BC相交于点D,然后根据三角形的一个外角大于任何一个与它不相邻的内角解答.
6.
--------------------------------------------------------------------------
B
7.
--------------------------------------------------------------------------
【答案】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.根据三角形的三边关系,可以首先确定一边,再加以分析.
有2,3,4;3,3,3;4,4,1三种情况.
故选C.
8.
--------------------------------------------------------------------------
B【解答】解:∵∠B+∠BAE=90°,∠C+∠CAF=90°,∠B=∠C
∴∠1=∠2(①正确)
∵∠E=∠F=90°,∠B=∠C,AE=AF
∴△ABE≌△ACF(ASA)
∴AB=AC,BE=CF(②正确)
∵∠CAN=∠BAM,∠B=∠C,AB=AC
∴△ACN≌△ABM(③正确)
∴CN=BM(④不正确).
所以正确结论有①②③.
故答案为B.
【分析】由已知条件,可直接得到三角形全等,得到结论,采用排除法,对各个选项进行验证从而确定正确的结论.
9.
--------------------------------------------------------------------------
答案:A.
解:过点P作MN⊥AD,交AD于M点,交BC于N点.
∵AD∥BC,MN⊥AD,
∴PN⊥BC.
∵PN⊥BC,PE⊥AB,PM⊥AD,BP为∠ABC的平分线,AP为∠BAD的平分线且相交于点P,
∴PM=PE=2,PE=PN=2.
∴MN=2+2=4,即两平行线AD与BC间的距离为4.
故选A.
【考点提示】
本题主要考查的是角平分线的性质,熟练掌握角平分线的性质是解题的关键;
【解题方法提示】
过点P作MN⊥AD,交AD于M点,交BC于N点,首先证明PN⊥BC,然后依据角平分线的性质可得到PM=PE=2,PE=PN=2;
最后,依据MN=PM+PN求解即可,赶快动手试试吧!
10.
--------------------------------------------------------------------------
A.
试题解析:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°?∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△ABG
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=(6+4)×16-3×4-6×3=50.
故选A.
考点:1.全等三角形的判定与性质,2.勾股定理
11.
--------------------------------------------------------------------------
解析根据题意知,本题可以直接根据三角形的外角性质,即三角形的外角等于不相邻的两内角之和,进行计算.
答案解:根据三角形的外角性质得∠A=∠ACD-∠B=120°-40°=80°.
故答案为:80°
点评根据本题题干及题意可知,这是一道考查三角形外角性质的题,牢牢掌握三角形的外角等于不相邻的两内角之和是解题的关键,这样可以提高解题的速度和准确率.
12.
--------------------------------------------------------------------------
【解答】解:可补充AF=CD或∠B=∠DEC;
当AF=CD时,三条边对应相等,所以两三角形全等;
当∠B=∠DEC时,两边夹一角,也全等.
故填AF=CD或∠B=∠DEC.
【分析】要使△ABF≌△DEC,已知AB=ED,EB=∠CF,具备了两组边对应相等,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.
13.
--------------------------------------------------------------------------
解:∵∠A+∠B+∠C=180°,∠C=4∠A,
∴∠A+∠B+4∠A=180°,
∵∠A+∠B=100°,
∴∠B=100°-∠A,
∴∠A+∠100°-∠A+4∠A=180°,
∴∠A=20°,
故答案为20°.
根据三角形内角和定理计算即可.
14.
--------------------------------------------------------------------------
2
【解答】解:∵三角形的三边长分别为1,x,2,
∴第三边的取值范围为:1<x<3
∵x为整数,
∴x=2.
故答案为:2.
【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,求解即可.
15.
--------------------------------------------------------------------------
解:由题意得:α=2β,α=100°,则β=50°,
180°-100°-50°=30°,
故答案为:30°.
此题考查了三角形内角和定理.解答此题时就是先根据已知一个内角α是另一个内角β的两倍得出β的度数,再根据三角形的内角和进而求出最小内角即可.
16.
--------------------------------------------------------------------------
解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
∵△ABC的面积为24,BD=CD,
∴S△ABD=S△ACD=×S△ABC=12,
又∵E是AD中点,
∴S△ABE=S△BDE=×S△ABD=6,
在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=CD,
∴S△BCF=4y,
则有,
解得,
则△AEF的面积为2.
故答案为:2.
先过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,由于△ABC的面积为24,BD=CD,可求S△ABD,S△ACD,又因为E是AD中点,可求S△ABE.在△ADG中,DG∥BF,E是AD中点,利用平行线分线段成比例定理的推论,可知AF=FG,从而可知△AEF∽△ADG,再利用相似三角形的面积比等于相似比的平方,可得∴S△ADG=4x,同理可求S△BCF=4y,再利用三角形面积之间的加减关系可得关于x、y的二元一次方程,求解即可.
17.
--------------------------------------------------------------------------
1)∠E(或∠DEF);两直线平行,同位角相等;
AB;已知;SAS(或边角边);全等三角形的对应角
(2)全等三角形的对应角;同错角相等,两直线平行;
18.
--------------------------------------------------------------------------
解:如图所示,点P就是所求的点.
使P到点M,N的距离相等,即画MN的垂直平分线,且到∠AOB的两边的距离相等,即画它的角平分线,两线的交点就是点P的位置.
19.
--------------------------------------------------------------------------
解:根据三角形内角和定理可得出
∠ACB=180°-40°-72°=68°,∵CE是∠ACB的平分线,∴∠BCE=34°;
∵CE是∠ACB的平分线,
∴∠BCE=34°,
∴∠BCD=180°-72°-90°=18°,
∴∠ECD=34°-18°=16°;
∵DF⊥CE,∠ECD=16°,
∴∠CDF=180°-16°-90°=74°.
利用直角三角形内角性质求角的度数
20.
--------------------------------------------------------------------------
解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM=
AE,BN=CN=DN=
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.
【分析】根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM=
AE,BN=CN=DN=
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
21.
--------------------------------------------------------------------------
(1)证明:∵BG//AC,
∴∠BGF=∠CFG,∠DBG=∠DCF,
∵D是BC的中点,
∴BD=CD,
∴△BDG≌△CDF,
∴BG=CF。
(2)解:BE+CF>EF。
证明:由(1)可得△BDG≌△CDF,
∴GD=FD,
又因为DE
⊥GF,
∴∠EDG=∠EDF=90°,
且ED=ED,
∴△EDG≌△EDF,
∴EG=EF,
在△BEG中,BG+BE>EG,
∴BE+CF=BE+BG>EG=EF,
∴BE+CF>EF。
【分析】(1)证明△BDG≌△CDF即可得到BG=CF;
(2)BE+CF与EF的关系,不能直接证明;由(1)可得CF=BG,容易得到BE+CF=BE+BG>EG,从而需要证明EG与EF的关系;由(1)可得GD=DF,即需要证明△EDG≌△EDF,可得到EG=EF。
22.
--------------------------------------------------------------------------
解:(1)∠BOC=180°-(∠1+∠2)又有2(∠1+∠2)=180°-∠A则∠1+∠2=90°-
∠A(2)∠BOC=
∠A(3)①△ADE和△EPB中有∠D+∠DAE=∠P+∠PBE即∠D+
∠DAC=∠P+
∠CBD同理②在△BCF和△PAF中有∠C+
∠CBD=∠P+
∠DAC,①+②就得∠P=
(∠C+∠D)(4)∠P=90°+
(∠C+∠D)故答案为:(1)(3)略(2)∠BOC=
∠A(4)∠P=90°+
(∠C+∠D)
由三角形的角平分线性质找出角的关系,再根据三角形内角和确定各角关系.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
