浙教版九年级上册第3章圆的基本性质单元测试卷(Word版含答案)
文档属性
| 名称 | 浙教版九年级上册第3章圆的基本性质单元测试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 854.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 14:07:07 | ||
图片预览


文档简介
圆的基本性质单元测试卷
一、选择题
1、下列命题中不正确的是(
)
A.圆有且只有一个内接三角形;
B.三角形的外心是这个三角形任意两边的垂直平分线的交点;
C.三角形只有一个外接圆;
D.等边三角形的外心也是三角形的三条中线、高、角平分线的交点.
2、过⊙内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为(?
)
(A)3cm
(B)6cm
(C)cm
(D)9cm
如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,
则∠AOD=(
)
A70°
B、60°
C、50°
D、40°
4、如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是(
)
A、15
B、20
C、
D、
(第3题)
(第4题)
(第5题)
(第6题)
5、如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿O—C—D—O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t之间函数关系最恰当的是(
)
A
B
C
D
6、如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AC的长等于(
)
A、
B、5
C、
D、6
7.如图,圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为(
)
A.
60πcm2 B.
45πcm2 C.
30πcm2 D15πcm2
(第7题)
(第8题)
(第9题)
8.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为
(
)
A.12个单位
B.10个单位
C.4个单位
D.15个单位
9.如图,有一块边长为6
cm的正三角形ABC木块,点P是边CA延长线上的一点,在A、P之间拉一细绳,绳长AP为15
cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)(
)
A.28.3
cm
B.28.2
cm
C.56.5
cm
D.56.6
cm
10、如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O,H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分的面积)为(
)
A、
B、
C、
D、
二、填空题(每题4分,共32分)
11.在半径为5厘米的圆内有两条互相平行的弦,一条弦长为8厘米,另一条弦长为6厘米,则两弦之间的距离为_______.
12.同圆的内接正三角形与内接正方形的边长的比是______.
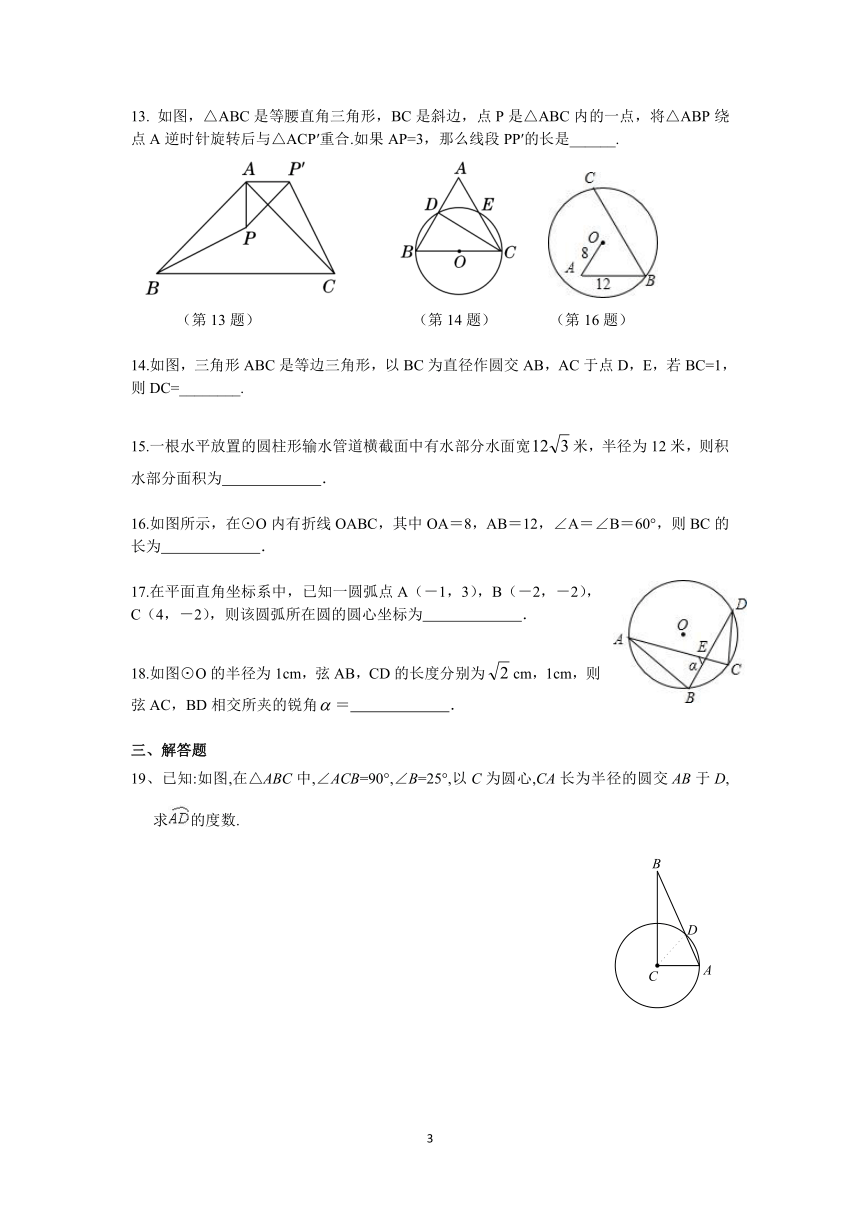
13.
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内的一点,将△ABP绕点A逆时针旋转后与△ACP′重合.如果AP=3,那么线段PP′的长是______.
(第13题)
(第14题)
(第16题)
14.如图,三角形ABC是等边三角形,以BC为直径作圆交AB,AC于点D,E,若BC=1,则DC=________.
15.一根水平放置的圆柱形输水管道横截面中有水部分水面宽米,半径为12米,则积水部分面积为
.
16.如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为
.
17.在平面直角坐标系中,已知一圆弧点A(-1,3),B(-2,-2),C(4,-2),则该圆弧所在圆的圆心坐标为
.
18.如图⊙O的半径为1cm,弦AB,CD的长度分别为cm,1cm,则弦AC,BD相交所夹的锐角=
.
三、解答题
19、已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
20、
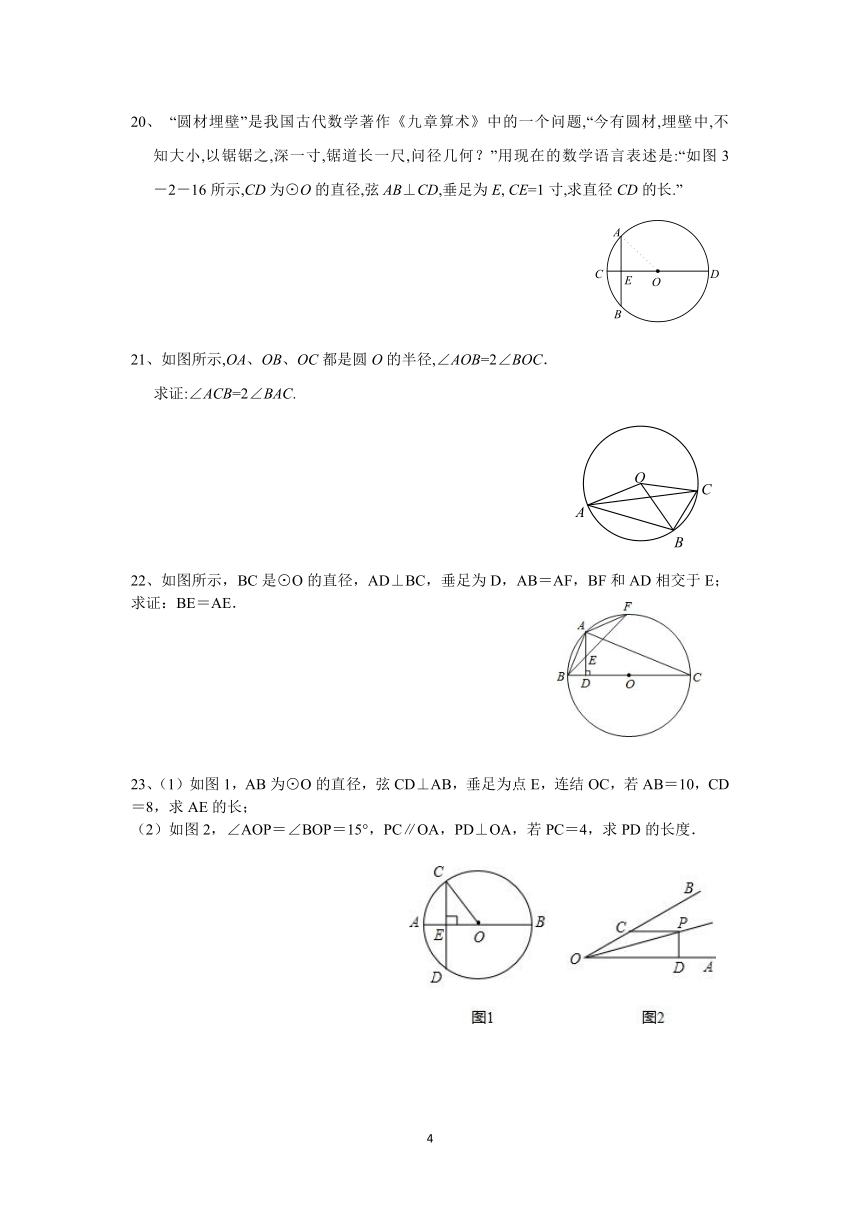
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图3-2-16所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,
CE=1寸,求直径CD的长.”
21、如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
(?http:?/??/?www.czsx.com.cn?)
22、如图所示,BC是⊙O的直径,AD⊥BC,垂足为D,AB=AF,BF和AD相交于E;求证:BE=AE.
23、(1)如图1,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长;
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
24、如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;(2)当AB=5,BC=6,求⊙O的半径.
(第24题)
25、如图所示,已知⊙O的直径为,AB为⊙O的弦,且AB=4,
P是⊙O上一动点,问是否存在以A,P,B为顶点的面积最大的三角形,试说明理由,若存在,求出这个三角形的面积.
26、如图所示,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C与A不重合,点D与B不重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出说明,并求出这个定值;若不是,请说明理由.
27、一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与C
D是水平的,BC与水平面的夹角为600,其中AB=60cm,CD=40cm,BC=40cm,请你做出该小朋友将圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度.
(?http:?/??/?www.czsx.com.cn?)
参考答案:
1~5:AADCC
6~10:ADBCC
11.
7厘米或1厘米
12.
13.
点拨:由旋转的性质,知∠PAP′等于90°,AP′=AP=3,所以PP′=
==.
14.
15、
16、20
17、(1,0)
18、75°
19、50°
20、26寸
21、求证圆周角∠ACB=2∠BAC,只要证明弧AB的度数是弧BC度数的两倍即可,由已知条件∠AOB=2∠BOC容易得到.
证明:∵BC是⊙O的直径,∴∠BAC=90°,
∵AD⊥BC,
∴∠BAD+∠CAD=∠CAD+∠C=90°,∴∠BAD=∠C,
∵AB=AF,∴∠ABF=∠C,∴∠BAD=∠ABF,∴BE=AE
解:(1)∵AB为⊙O的直径,弦CD⊥AB
∴CE=DE,
∵AB=10,CD=8,∴OC=5,CE=4,∴OE=3,∴AE=2
(2)2
24、(1)证明:∵AB=AC,点D在弧BC上运动,过点D作DE∥BC,∴=,
∠ABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB,∴∠ADB=∠E;
(2)解:连结AO并延长交BC于F,连结OB,OC,
∵AB=AC,OB=OC,∴AO垂直平分BC,∴BF=CF=BC=×6=3,
在直角△ABF中,由勾股定理可得AF=4,设⊙O的半径为r,
在直角△OBF中,OB=r,BF=3,OF=4-r,
∴,解得,∴⊙O的半径是
25.解:存在以A,P,B为顶点的面积最大的三角形.
如答图6所示,作PD⊥AB于点D,
∵当点P在优弧AB上时,PD可能大于⊙O的半径,当点P在劣弧AB上时,PD一定小于⊙O的半径,且AB的长为定值,
∴当点P在优弧AB上且为优弧AB的中点时△APB的面积最大,
此时PD经过圆心O.作⊙O的直径AC,连结BC,
则∠ABC=90°.∴BC===2
.∵AO=OC,AD=BD,
∴OD为△ABC的中位线,OD==.∴PD=PO+OD=+=
.∴=·PD=×4×=.
(1)证明:过点O作OH⊥CD于点H,∴H为CD的中点
.∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,则O为EF的中点,OE=OF.
又∵AB为直径,∴OA=OB,∴AE=OA-OE=OB-OF=BF,即AE=BF.
解:四边形CDFE的面积为定值,是.理由:
∵动弦CD在滑动过程中,条件EC⊥CD,FD⊥CD不变,
∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,
∴=OH·CD.连结OC.∴OH===(cm)
.又∵CD为定值8
cm,
∴=OH·CD=×8=(),是常数.即四边形CDFE的面积为定值.
27.示意图略,路线的长度为140-
HYPERLINK
"http://www.czsx.com.cn"
一、选择题
1、下列命题中不正确的是(
)
A.圆有且只有一个内接三角形;
B.三角形的外心是这个三角形任意两边的垂直平分线的交点;
C.三角形只有一个外接圆;
D.等边三角形的外心也是三角形的三条中线、高、角平分线的交点.
2、过⊙内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为(?
)
(A)3cm
(B)6cm
(C)cm
(D)9cm
如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,
则∠AOD=(
)
A70°
B、60°
C、50°
D、40°
4、如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是(
)
A、15
B、20
C、
D、
(第3题)
(第4题)
(第5题)
(第6题)
5、如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿O—C—D—O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t之间函数关系最恰当的是(
)
A
B
C
D
6、如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AC的长等于(
)
A、
B、5
C、
D、6
7.如图,圆锥的底面半径为3cm,母线长为5cm,则它的侧面积为(
)
A.
60πcm2 B.
45πcm2 C.
30πcm2 D15πcm2
(第7题)
(第8题)
(第9题)
8.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为
(
)
A.12个单位
B.10个单位
C.4个单位
D.15个单位
9.如图,有一块边长为6
cm的正三角形ABC木块,点P是边CA延长线上的一点,在A、P之间拉一细绳,绳长AP为15
cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)(
)
A.28.3
cm
B.28.2
cm
C.56.5
cm
D.56.6
cm
10、如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O,H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分的面积)为(
)
A、
B、
C、
D、
二、填空题(每题4分,共32分)
11.在半径为5厘米的圆内有两条互相平行的弦,一条弦长为8厘米,另一条弦长为6厘米,则两弦之间的距离为_______.
12.同圆的内接正三角形与内接正方形的边长的比是______.
13.
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内的一点,将△ABP绕点A逆时针旋转后与△ACP′重合.如果AP=3,那么线段PP′的长是______.
(第13题)
(第14题)
(第16题)
14.如图,三角形ABC是等边三角形,以BC为直径作圆交AB,AC于点D,E,若BC=1,则DC=________.
15.一根水平放置的圆柱形输水管道横截面中有水部分水面宽米,半径为12米,则积水部分面积为
.
16.如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为
.
17.在平面直角坐标系中,已知一圆弧点A(-1,3),B(-2,-2),C(4,-2),则该圆弧所在圆的圆心坐标为
.
18.如图⊙O的半径为1cm,弦AB,CD的长度分别为cm,1cm,则弦AC,BD相交所夹的锐角=
.
三、解答题
19、已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
20、
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图3-2-16所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,
CE=1寸,求直径CD的长.”
21、如图所示,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
(?http:?/??/?www.czsx.com.cn?)
22、如图所示,BC是⊙O的直径,AD⊥BC,垂足为D,AB=AF,BF和AD相交于E;求证:BE=AE.
23、(1)如图1,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长;
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
24、如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;(2)当AB=5,BC=6,求⊙O的半径.
(第24题)
25、如图所示,已知⊙O的直径为,AB为⊙O的弦,且AB=4,
P是⊙O上一动点,问是否存在以A,P,B为顶点的面积最大的三角形,试说明理由,若存在,求出这个三角形的面积.
26、如图所示,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C与A不重合,点D与B不重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出说明,并求出这个定值;若不是,请说明理由.
27、一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与C
D是水平的,BC与水平面的夹角为600,其中AB=60cm,CD=40cm,BC=40cm,请你做出该小朋友将圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度.
(?http:?/??/?www.czsx.com.cn?)
参考答案:
1~5:AADCC
6~10:ADBCC
11.
7厘米或1厘米
12.
13.
点拨:由旋转的性质,知∠PAP′等于90°,AP′=AP=3,所以PP′=
==.
14.
15、
16、20
17、(1,0)
18、75°
19、50°
20、26寸
21、求证圆周角∠ACB=2∠BAC,只要证明弧AB的度数是弧BC度数的两倍即可,由已知条件∠AOB=2∠BOC容易得到.
证明:∵BC是⊙O的直径,∴∠BAC=90°,
∵AD⊥BC,
∴∠BAD+∠CAD=∠CAD+∠C=90°,∴∠BAD=∠C,
∵AB=AF,∴∠ABF=∠C,∴∠BAD=∠ABF,∴BE=AE
解:(1)∵AB为⊙O的直径,弦CD⊥AB
∴CE=DE,
∵AB=10,CD=8,∴OC=5,CE=4,∴OE=3,∴AE=2
(2)2
24、(1)证明:∵AB=AC,点D在弧BC上运动,过点D作DE∥BC,∴=,
∠ABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB,∴∠ADB=∠E;
(2)解:连结AO并延长交BC于F,连结OB,OC,
∵AB=AC,OB=OC,∴AO垂直平分BC,∴BF=CF=BC=×6=3,
在直角△ABF中,由勾股定理可得AF=4,设⊙O的半径为r,
在直角△OBF中,OB=r,BF=3,OF=4-r,
∴,解得,∴⊙O的半径是
25.解:存在以A,P,B为顶点的面积最大的三角形.
如答图6所示,作PD⊥AB于点D,
∵当点P在优弧AB上时,PD可能大于⊙O的半径,当点P在劣弧AB上时,PD一定小于⊙O的半径,且AB的长为定值,
∴当点P在优弧AB上且为优弧AB的中点时△APB的面积最大,
此时PD经过圆心O.作⊙O的直径AC,连结BC,
则∠ABC=90°.∴BC===2
.∵AO=OC,AD=BD,
∴OD为△ABC的中位线,OD==.∴PD=PO+OD=+=
.∴=·PD=×4×=.
(1)证明:过点O作OH⊥CD于点H,∴H为CD的中点
.∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,则O为EF的中点,OE=OF.
又∵AB为直径,∴OA=OB,∴AE=OA-OE=OB-OF=BF,即AE=BF.
解:四边形CDFE的面积为定值,是.理由:
∵动弦CD在滑动过程中,条件EC⊥CD,FD⊥CD不变,
∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,
∴=OH·CD.连结OC.∴OH===(cm)
.又∵CD为定值8
cm,
∴=OH·CD=×8=(),是常数.即四边形CDFE的面积为定值.
27.示意图略,路线的长度为140-
HYPERLINK
"http://www.czsx.com.cn"
同课章节目录
