浙教版数学九年级上册3.5 圆周角圆周角定理应用训练(Word版 含解析)
文档属性
| 名称 | 浙教版数学九年级上册3.5 圆周角圆周角定理应用训练(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 879.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览



文档简介
圆周角定理练习题
一.选择题(共16小题)
1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
A.30°
B.35°
C.40°
D.45°
第1题图
第2题图
第3题图
3.如图,在图中标出的4个角中,圆周角有( )个.
A.1
B.2
C.3
D.4
4.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是( )
A.25°
B.30°
C.40°
D.50°
5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )A.130°
B.140°
C.145°
D.150°
第4题图
第5题图
第6题图
6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于( )
A.50°
B.40°
C.30°
D.20°
7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为)
A.40°
B.50°
C.60°
D.70°
8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
第7题图
第8题图
第9题图
9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°
C.35°
D.50°
10.如图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
11.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )
A.30°
B.45°
C.60°
D.90°
第10题图
第11题图
第12题图
12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
A.15°
B.20°
C.25°
D.50°
13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是( )
A.42°
B.84°
C.42°或138°
D.84°或96°
14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于( )
A.90°
B.60°
C.45°
D.30°
15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为( )
A.60°
B.50°
C.40°
D.30°
第10题图
第11题图
第12题图
16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )
A.30°
B.50°
C.60°
D.70°
二.填空题(共8小题)
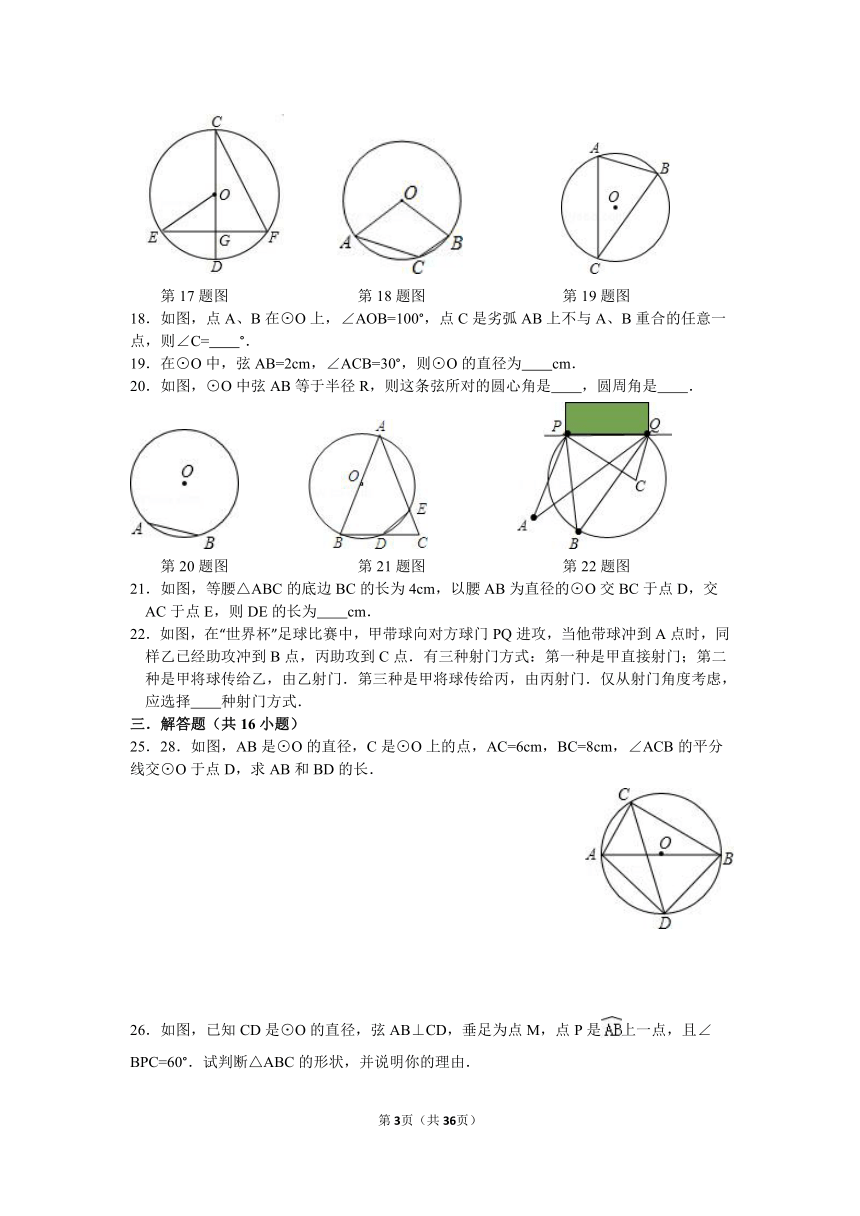
17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于 .
第17题图
第18题图
第19题图
18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= °.
19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 cm.
20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是 ,圆周角是 .
第20题图
第21题图
第22题图
21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 cm.
22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择 种射门方式.
三.解答题(共16小题)
25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.
26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.
求证:HD=GD.
28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°
(1)求∠EBC的度数;
(2)求证:BD=CD.
29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.
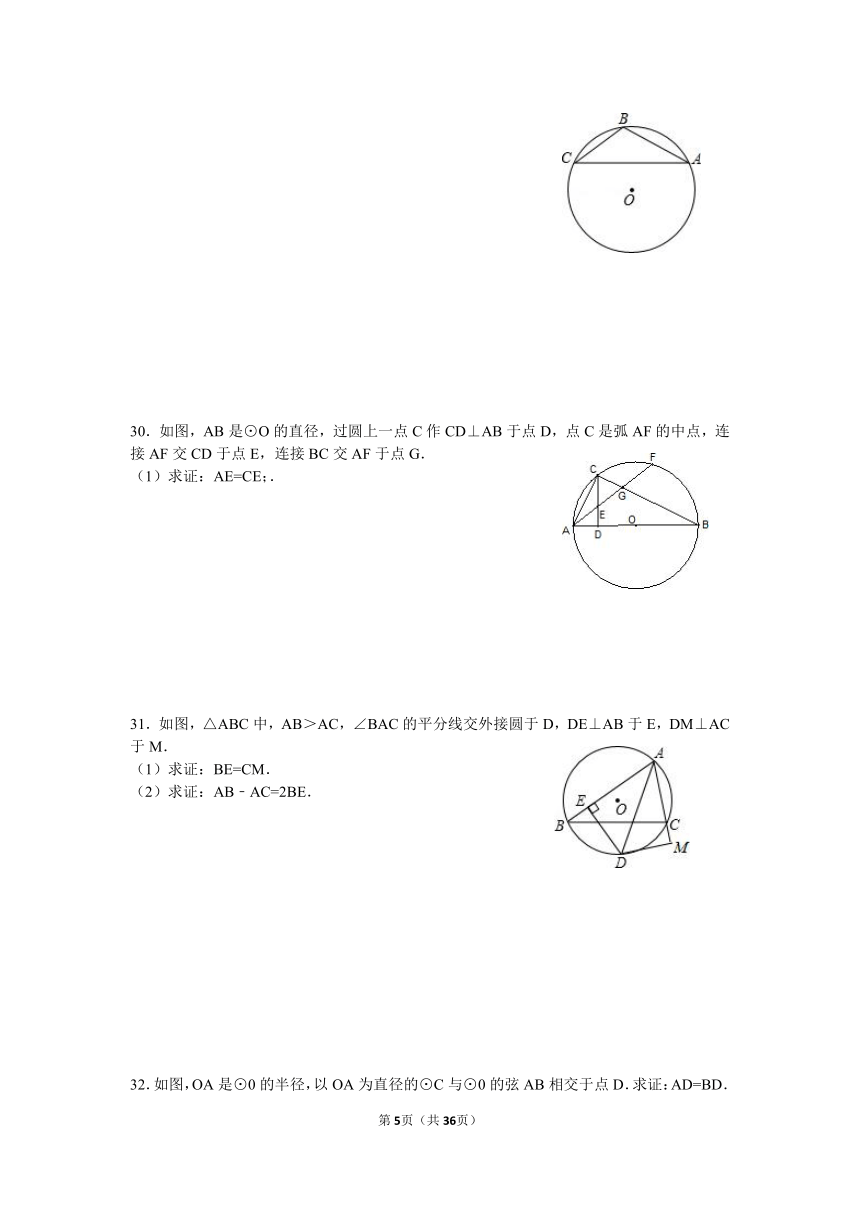
30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.
(1)求证:AE=CE;.
31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.
(1)求证:BE=CM.
(2)求证:AB﹣AC=2BE.
32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.
35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?
38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.
39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.
40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.
41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?
42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?
43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.
44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;
(2)∠A=∠GEF.
45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.
《圆周角定理》
参考答案与试题解析
一.选择题(共16小题)
1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,
又∵∠BOC=76°,
∴∠A=76°×=38°.
故选C.
2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
A.30°
B.35°
C.40°
D.45°
【解答】解:∵OA=OC,∠ACO=45°,
∴∠OAC=45°,
∴∠AOC=180°﹣45°﹣45°=90°,
∴∠B=∠AOC=45°.
故选D.
3.如图,在图中标出的4个角中,圆周角有( )个.
A.1
B.2
C.3
D.4
【解答】解:∠1和∠3符合圆周角的定义,
∠2顶点不在圆周上,
∠4的一边不和圆相交,
故图中圆周角有∠1和∠3两个.
故选B.
4.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是( )
A.25°
B.30°
C.40°
D.50°
【解答】解:∵在⊙O中,直径CD垂直于弦AB,
∴=,
∴∠DOB=2∠C=50°.
故选:D.
5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )
A.130°
B.140°
C.145°
D.150°
【解答】解:设点E是优弧AB上的一点,连接EA,EB
∵∠AOB=80°
∴∠E=∠AOB=40°
∴∠ACB=180°﹣∠E=140°.
故选:B.
6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于( )
A.50°
B.40°
C.30°
D.20°
【解答】解:连接OP,
可得∠MAP=∠MOP,∠NBP=∠NOP,
∵MN为直径,
∴∠MOP+∠NBP=180°,
∴∠MAP+∠NBP=90°,
∵∠PBN=50°,
∴∠MAP=90°﹣∠PBN=40°.
故选B.
7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为( )
A.40°
B.50°
C.60°
D.70°
【解答】解:∵∠ABD=20°
∴∠C=∠ABD=20°
∵CD是⊙O的直径
∴∠CAD=90°
∴∠ADC=90°﹣20°=70°.
故选D.
8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
【解答】解:连结BD,如图,
∵点D是的中点,即弧CD=弧AD,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣25°=65°.
故选C.
9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°
C.35°
D.50°
【解答】解:∵∠AOC=130°,
∴∠BOC=50°,
∴∠D=∠BOC=25°.故选A.
10.如图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,
根据三角形的外角的性质得:∠5>∠4,∠2>∠6,
∴∠4<∠1=∠3<∠2,
故选B.
11.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )
A.30°
B.45°
C.60°
D.90°
【解答】解:连接BC,
∵AB是半圆的直径
∴∠ACB=90°
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=30°,
∴∠D=∠ABC=30°.
故选A.
12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
A.15°
B.20°
C.25°
D.50°
【解答】解:∵OA⊥BC,∠AOC=50°,
∴,
∴∠ADB=∠AOC=25°.
故选C.
13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是( )
A.42°
B.84°
C.42°或138°
D.84°或96°
【解答】解:如图,∵∠AOB=84°,
∴∠ACB=∠AOB=×84°=42°,
∴∠ADB=180°﹣∠ACB=138°.
∴弦AB所对的圆周角是:42°或138°.
故选C.
14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于( )
A.90°
B.60°
C.45°
D.30°
【解答】解:连接AD,
∵在⊙O中,AB是⊙O的直径,
∴∠ADB=90°,
∵CD是∠ACB的角平分线,
∴=,
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABD=45°.
故选C.
15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为( )
A.60°
B.50°
C.40°
D.30°
【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=40°,
∴∠CBA=90°﹣∠A=50°.
故选B.
16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )
A.30°
B.50°
C.60°
D.70°
【解答】解:∵∠BAD=30°,
∴=60°,
∵AB是圆的直径,AB⊥CD,
∴==60°,
∴=180°﹣60°=120°,
∴∠AEC==×120°=60°.
故选C.
二.填空题(共8小题)
17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于 40° .
【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,
∴弧DF=弧DE,且弧的度数是40°,
∴∠DOE=40°,
答案为40°.
18.如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是 65° .
【解答】解:连结BD,如图,
∵点D是
的中点,即弧CD=弧AD,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣25°=65°.
故答案为65°.
19.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= 130 °.
【解答】解:在优弧AB上取点D,连结AD、BD,如图,
∴∠D=∠AOB=×100°=50°,
∵∠D+∠C=180°,
∴∠C=180°﹣50°=130°.
故答案为130.
20.球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 第二种 种射门方式较为合理.
【解答】解:连接OC.
根据圆周角定理,得∠PCQ=∠B,
根据三角形的外角的性质,得∠PCQ>∠A,
则∠B>∠A.
故答案为第二种.
21.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 4 cm.
【解答】解:连接OA,OB,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2cm,
∴⊙O的直径=4cm.
故答案为:4.
22.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是 60° ,圆周角是 30°或150° .
【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,
∵弦AB等于半径R,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∴∠AP′B=180°﹣∠APB=150°,
即这条弦所对的圆心角是60°,圆周角是30°或150°.
故答案为60°;是30°或150°.
23.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 2 cm.
【解答】
解:连接AD,
∵∠DEC为圆内接四边形ABDE的外角,
∴∠DEC=∠B,
又等腰△ABC,BC为底边,
∴AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∴DE=DC,
∵AB为圆O的直径,
∴∠ADB=90°,即AD⊥BC,
∴BD=CD=BC,又BC=4cm,
∴DE=2cm.
故答案为:2
24.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择 第二 种射门方式.
【解答】解:设AP与圆的交点是C,连接CQ;
则∠PCQ>∠A;
由圆周角定理知:∠PCQ=∠B;
所以∠B>∠A;
因此选择第二种射门方式更好.
故答案为:第二.
三.解答题(共16小题)
25.如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.
求证:HD=GD.
【解答】证明:∵∠C=∠G,△ABC的高AD、BE,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE,
∵∠AHE=∠BHG=∠C,
∴∠G=∠BHG,
∴BH=BG,
又∵AD⊥BC,
∴HD=DG.
26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
【解答】解:△ABC为等边三角形.理由如下:
∵AB⊥CD,CD为⊙O的直径,
∴弧AC=弧BC,
∴AC=BC,
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
27.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°
(1)求∠EBC的度数;
(2)求证:BD=CD.
【解答】(1)解:∵AB=AC,
∴∠ABC=∠C,
∵∠BAC=40°,
∴∠C=(180°﹣40°)=70°,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠EBC=90°﹣∠C=20°;
证明:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=DC.
28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.
【解答】解:如图,∵AB是⊙O的直径,
∴∠ACB=90°,∠ADB=90°.
∴AB===10(cm).
∵AC=6cm,BC=8cm,
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD,则=,
∴AD=BD,
∴BD=AB=5cm.
综上所述,AB和BD的长分别是10cm,5cm.
29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.
【解答】解:作直径CD,连结BD,如图,
∵CD为直径,
∴∠CBD=90°,
∵∠D=∠A=30°,
∴CD=2BC=2×3=6,
∴⊙O的半径为3cm.
30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.
(1)求证:AE=CE;
(2)已知AG=10,ED:AD=3:4,求AC的长.
【解答】(1)证明:∵点C是弧AF的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACE+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠CAE=∠ACE,
∴AE=CE
…(6分)
(2)解:∵∠ACB=90°,
∴∠CAE+∠CGA=90°,
又∵∠ACE+∠BCD=90°,
∴∠CGA=∠BCD,
∵AG=10,
∴CE=EG=AE=5,
∵ED:AD=3:4,
∴AD=4,DE=3,
∴AC=…(10分).
31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.
(1)求证:BE=CM.
(2)求证:AB﹣AC=2BE.
【解答】证明:(1)连接BD,DC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴弧BD=弧CD,
∴BD=CD,
∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,
∵∠M=∠DEB=90°,DE=DM,
在Rt△DEB和Rt△DMC中,
,
∴Rt△DEB≌Rt△DMC(HL),
∴BE=CM.
(2)∵DE⊥AB,DM⊥AC,
∵∠M=∠DEA=90°,
在Rt△DEA和Rt△DMA中
∴Rt△DEA≌Rt△DMA(HL),
∴AE=AM,
∴AB﹣AC,
=AE+BE﹣AC,
=AM+BE﹣AC,
=AC+CM+BE﹣AC,
=BE+CM,
=2BE.
32.(2013?宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
【解答】证明:连结OD,如图,
∵OA为⊙C的直径,
∴∠ADO=90°,
∴OD⊥AB,
∴AD=BD.
33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
【解答】解:连接OM
∵OD=OM,
∴∠ODM=∠OMD,
∵DM平分∠ODC,
∴∠ODM=∠CDM,
∴∠CDM=∠OMD,
∴CD∥OM,
∵CD⊥AB,
∴OM⊥AB,
∴弧AM=弧BM,
即点M为劣弧AB的中点.
34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.
【解答】解:连接AE,
∵CE为直径,
∴∠EAC=90°,
∴∠ACE=90°﹣∠AEC,
∵CD是高,D是垂足,
∴∠BCD=90°﹣∠B,
∵∠B=∠AEC(同弧所对的圆周角相等),
∴∠ACE=∠BCD,
∴∠ACE+∠ECD=∠BCD+∠ECD,
∴∠ACD=∠BCE.
35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
【解答】证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠BAE=90°,
∵AF⊥BC于D,
∴∠FAC+∠ACB=90°,
∵∠E=∠ACB,
∴∠BAE=∠FAC,
∴弧BE=弧CF,
∴BE=CF.
36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
【解答】证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠AEB=∠AEC=90°,
∵弦BE=DE,
∴=,
∴∠DAE=∠BAE,
∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,
∴∠B=∠C,
∴AC=AB.
37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?
【解答】解:AD和BF相等.理由:如图,
连接AC、BC,
∵OC⊥AB,
∴∠BOC=90°
∴∠BDC=∠BAC=45°
∵EC⊥CD,
∴∠DCE=∠ACB=90°,
∴△DCF和△ACB都是等腰直角三角形,
∴DC=FC,AC=BC,
∵∠DCA+∠ACF=∠BCF+∠ACF=90°,
∴∠DCA=∠FCB
在△ACD和△BCF中,
{,∴△ACD≌△BCF
∴DA=BF.
38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.
【解答】证明:连接AD,AE,
∵AB是直径.AB⊥DE,
∴AB平分DE,弧ACE=弧AD,
∴∠ACD=∠ADE,
∵A、C、E、D四点共圆,
∴∠FCE=∠ADE,
∴∠FCE=∠ACD,
∴∠FCE+∠DCE=∠DAC+∠ECD,
∴∠FCD=∠ACE.
39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.
【解答】解:
延长CE交⊙O于M,
∵AD是⊙O的直径,作CE⊥AD,
∴弧AC=弧AM,
∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).
40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.
【解答】解:△DBC为等腰三角形.理由如下:
∵AD为△ABC的外角平分线,
∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DBC=∠DAC,
∴∠DBC=∠DCB,
∴△DBC为等腰三角形.
一.解答题(共6小题)
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?
【解答】解:∠FGC与∠AGD相等.理由如下:
连接AD,如图,
∵CD⊥AB,
∴=,
∴∠AGD=∠ADC,
∵∠FGC=∠ADC,
∴∠FGC=∠AGD
2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?
【解答】解:AF=FG,
理由是:连接AD,
∵AB是直径,DE⊥AB,
∴∠ADB=∠DEB=90°,
∴∠ADE=∠ABD,
∵D为弧AC中点,
∴∠DAC=∠ABD,
∴∠ADE=∠DAC,
∴AF=DF,∠FAE=∠DAC,
∴DF=FG,
∴AF=FG.
3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D点在⊙O上运动时(不与A重合),AE与ED的长度有何关系?证明你的结论.
【解答】解:AE=ED.
理由:连接OE,
∵AO是⊙C的直径,
∴∠OEA=90°,
∴OE⊥AD,
∵OE过圆O的圆心O,
∴AE=ED.
4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.
【解答】证明:连接OD,
∵OA为⊙C的直径,
∴∠ODA=90°,即OD⊥AB,
∴D是AB的中点.
5.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;
(2)∠A=∠GEF.
【解答】证明一:
(1)连接DF,∵∠ACB=90°,D是AB的中点,
∴BD=DC=AB,(2分)
∵DC是⊙O的直径,
∴DF⊥BC,(4分)
∴BF=FC,即F是BC的中点;(5分)
(2)∵D,F分别是AB,BC的中点,
∴DF∥AC,(6分)
∴∠A=∠BDF,(7分)
∵∠BDF=∠GEF(圆周角定理),(8分)
∴∠A=∠GEF.(9分)
证明二:
(1)连接DF,DE,
∵DC是⊙O直径,
∴∠DEC=∠DFC=90°.(1分)
∵∠ECF=90°,
∴四边形DECF是矩形.
∴EF=CD,DF=EC.(2分)
∵D是AB的中点,∠ACB=90°,
∴EF=CD=BD=AB.(3分)
∴△DBF≌△EFC.(4分)
∴BF=FC,即F是BC的中点.(5分)
(2)∵△DBF≌△EFC,
∴∠BDF=∠FEC,∠B=∠EFC.(6分)
∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),
∴∠A=∠FEC.(7分)
∵∠FEG=∠BDF(同弧所对的圆周角相等
),(8分)
∴∠A=∠GEF.(9分)
(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)
6.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.
【解答】证明:(1)在△DHC与△DPC中,
∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,
∴△DHC≌△DPC,
∴CH=CP.
(2)连接DB,由圆周角定理得,
∠DAC=∠DBH,
∵△DHC≌△DPC,
∴DH=DP,
∵DP⊥AC,DH⊥BH,
∴∠DHB=∠DPC=90°,
∴△DAP≌△DBH,
∴AP=BH.
第10页(共36页)
一.选择题(共16小题)
1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
A.30°
B.35°
C.40°
D.45°
第1题图
第2题图
第3题图
3.如图,在图中标出的4个角中,圆周角有( )个.
A.1
B.2
C.3
D.4
4.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是( )
A.25°
B.30°
C.40°
D.50°
5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )A.130°
B.140°
C.145°
D.150°
第4题图
第5题图
第6题图
6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于( )
A.50°
B.40°
C.30°
D.20°
7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为)
A.40°
B.50°
C.60°
D.70°
8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
第7题图
第8题图
第9题图
9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°
C.35°
D.50°
10.如图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
11.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )
A.30°
B.45°
C.60°
D.90°
第10题图
第11题图
第12题图
12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
A.15°
B.20°
C.25°
D.50°
13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是( )
A.42°
B.84°
C.42°或138°
D.84°或96°
14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于( )
A.90°
B.60°
C.45°
D.30°
15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为( )
A.60°
B.50°
C.40°
D.30°
第10题图
第11题图
第12题图
16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )
A.30°
B.50°
C.60°
D.70°
二.填空题(共8小题)
17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于 .
第17题图
第18题图
第19题图
18.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= °.
19.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 cm.
20.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是 ,圆周角是 .
第20题图
第21题图
第22题图
21.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 cm.
22.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择 种射门方式.
三.解答题(共16小题)
25.28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.
26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
27、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.
求证:HD=GD.
28.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°
(1)求∠EBC的度数;
(2)求证:BD=CD.
29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.
30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.
(1)求证:AE=CE;.
31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.
(1)求证:BE=CM.
(2)求证:AB﹣AC=2BE.
32.如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.
35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?
38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.
39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.
40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.
41.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?
42.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?
43.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.
44.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;
(2)∠A=∠GEF.
45.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.
《圆周角定理》
参考答案与试题解析
一.选择题(共16小题)
1.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
【解答】解:∵所对的圆心角是∠BOC,圆周角是∠BAC,
又∵∠BOC=76°,
∴∠A=76°×=38°.
故选C.
2.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
A.30°
B.35°
C.40°
D.45°
【解答】解:∵OA=OC,∠ACO=45°,
∴∠OAC=45°,
∴∠AOC=180°﹣45°﹣45°=90°,
∴∠B=∠AOC=45°.
故选D.
3.如图,在图中标出的4个角中,圆周角有( )个.
A.1
B.2
C.3
D.4
【解答】解:∠1和∠3符合圆周角的定义,
∠2顶点不在圆周上,
∠4的一边不和圆相交,
故图中圆周角有∠1和∠3两个.
故选B.
4.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是( )
A.25°
B.30°
C.40°
D.50°
【解答】解:∵在⊙O中,直径CD垂直于弦AB,
∴=,
∴∠DOB=2∠C=50°.
故选:D.
5.如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )
A.130°
B.140°
C.145°
D.150°
【解答】解:设点E是优弧AB上的一点,连接EA,EB
∵∠AOB=80°
∴∠E=∠AOB=40°
∴∠ACB=180°﹣∠E=140°.
故选:B.
6.如图,MN是⊙O的直径,∠PBN=50°,则∠MAP等于( )
A.50°
B.40°
C.30°
D.20°
【解答】解:连接OP,
可得∠MAP=∠MOP,∠NBP=∠NOP,
∵MN为直径,
∴∠MOP+∠NBP=180°,
∴∠MAP+∠NBP=90°,
∵∠PBN=50°,
∴∠MAP=90°﹣∠PBN=40°.
故选B.
7.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为( )
A.40°
B.50°
C.60°
D.70°
【解答】解:∵∠ABD=20°
∴∠C=∠ABD=20°
∵CD是⊙O的直径
∴∠CAD=90°
∴∠ADC=90°﹣20°=70°.
故选D.
8.如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
【解答】解:连结BD,如图,
∵点D是的中点,即弧CD=弧AD,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣25°=65°.
故选C.
9.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°
C.35°
D.50°
【解答】解:∵∠AOC=130°,
∴∠BOC=50°,
∴∠D=∠BOC=25°.故选A.
10.如图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3
B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2
D.∠4<∠1<∠3=∠2
【解答】解:如图,利用圆周角定理可得:∠1=∠3=∠5=∠6,
根据三角形的外角的性质得:∠5>∠4,∠2>∠6,
∴∠4<∠1=∠3<∠2,
故选B.
11.如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是( )
A.30°
B.45°
C.60°
D.90°
【解答】解:连接BC,
∵AB是半圆的直径
∴∠ACB=90°
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=30°,
∴∠D=∠ABC=30°.
故选A.
12.如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
A.15°
B.20°
C.25°
D.50°
【解答】解:∵OA⊥BC,∠AOC=50°,
∴,
∴∠ADB=∠AOC=25°.
故选C.
13.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是( )
A.42°
B.84°
C.42°或138°
D.84°或96°
【解答】解:如图,∵∠AOB=84°,
∴∠ACB=∠AOB=×84°=42°,
∴∠ADB=180°﹣∠ACB=138°.
∴弦AB所对的圆周角是:42°或138°.
故选C.
14.如图所示,在⊙O中,AB是⊙O的直径,∠ACB的角平分线CD交⊙O于D,则∠ABD的度数等于( )
A.90°
B.60°
C.45°
D.30°
【解答】解:连接AD,
∵在⊙O中,AB是⊙O的直径,
∴∠ADB=90°,
∵CD是∠ACB的角平分线,
∴=,
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABD=45°.
故选C.
15.已知如图,AB是⊙O的直径,CD是⊙O的弦,∠CDB=40°,则∠CBA的度数为( )
A.60°
B.50°
C.40°
D.30°
【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=40°,
∴∠CBA=90°﹣∠A=50°.
故选B.
16.如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )
A.30°
B.50°
C.60°
D.70°
【解答】解:∵∠BAD=30°,
∴=60°,
∵AB是圆的直径,AB⊥CD,
∴==60°,
∴=180°﹣60°=120°,
∴∠AEC==×120°=60°.
故选C.
二.填空题(共8小题)
17.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于 40° .
【解答】解:∵⊙O的直径CD过弦EF的中点G,∠DCF=20°,
∴弧DF=弧DE,且弧的度数是40°,
∴∠DOE=40°,
答案为40°.
18.如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB的度数是 65° .
【解答】解:连结BD,如图,
∵点D是
的中点,即弧CD=弧AD,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣25°=65°.
故答案为65°.
19.如图,点A、B在⊙O上,∠AOB=100°,点C是劣弧AB上不与A、B重合的任意一点,则∠C= 130 °.
【解答】解:在优弧AB上取点D,连结AD、BD,如图,
∴∠D=∠AOB=×100°=50°,
∵∠D+∠C=180°,
∴∠C=180°﹣50°=130°.
故答案为130.
20.球员甲带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 第二种 种射门方式较为合理.
【解答】解:连接OC.
根据圆周角定理,得∠PCQ=∠B,
根据三角形的外角的性质,得∠PCQ>∠A,
则∠B>∠A.
故答案为第二种.
21.在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为 4 cm.
【解答】解:连接OA,OB,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2cm,
∴⊙O的直径=4cm.
故答案为:4.
22.如图,⊙O中弦AB等于半径R,则这条弦所对的圆心角是 60° ,圆周角是 30°或150° .
【解答】解:连结OA、OB,∠APB和∠AP′B为弦AB所对的圆周角,如图,
∵弦AB等于半径R,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∴∠AP′B=180°﹣∠APB=150°,
即这条弦所对的圆心角是60°,圆周角是30°或150°.
故答案为60°;是30°或150°.
23.如图,等腰△ABC的底边BC的长为4cm,以腰AB为直径的⊙O交BC于点D,交AC于点E,则DE的长为 2 cm.
【解答】
解:连接AD,
∵∠DEC为圆内接四边形ABDE的外角,
∴∠DEC=∠B,
又等腰△ABC,BC为底边,
∴AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∴DE=DC,
∵AB为圆O的直径,
∴∠ADB=90°,即AD⊥BC,
∴BD=CD=BC,又BC=4cm,
∴DE=2cm.
故答案为:2
24.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择 第二 种射门方式.
【解答】解:设AP与圆的交点是C,连接CQ;
则∠PCQ>∠A;
由圆周角定理知:∠PCQ=∠B;
所以∠B>∠A;
因此选择第二种射门方式更好.
故答案为:第二.
三.解答题(共16小题)
25.如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.
求证:HD=GD.
【解答】证明:∵∠C=∠G,△ABC的高AD、BE,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE,
∵∠AHE=∠BHG=∠C,
∴∠G=∠BHG,
∴BH=BG,
又∵AD⊥BC,
∴HD=DG.
26.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为点M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明你的理由.
【解答】解:△ABC为等边三角形.理由如下:
∵AB⊥CD,CD为⊙O的直径,
∴弧AC=弧BC,
∴AC=BC,
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
27.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°
(1)求∠EBC的度数;
(2)求证:BD=CD.
【解答】(1)解:∵AB=AC,
∴∠ABC=∠C,
∵∠BAC=40°,
∴∠C=(180°﹣40°)=70°,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠EBC=90°﹣∠C=20°;
证明:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=DC.
28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.
【解答】解:如图,∵AB是⊙O的直径,
∴∠ACB=90°,∠ADB=90°.
∴AB===10(cm).
∵AC=6cm,BC=8cm,
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD,则=,
∴AD=BD,
∴BD=AB=5cm.
综上所述,AB和BD的长分别是10cm,5cm.
29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.
【解答】解:作直径CD,连结BD,如图,
∵CD为直径,
∴∠CBD=90°,
∵∠D=∠A=30°,
∴CD=2BC=2×3=6,
∴⊙O的半径为3cm.
30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.
(1)求证:AE=CE;
(2)已知AG=10,ED:AD=3:4,求AC的长.
【解答】(1)证明:∵点C是弧AF的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACE+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠CAE=∠ACE,
∴AE=CE
…(6分)
(2)解:∵∠ACB=90°,
∴∠CAE+∠CGA=90°,
又∵∠ACE+∠BCD=90°,
∴∠CGA=∠BCD,
∵AG=10,
∴CE=EG=AE=5,
∵ED:AD=3:4,
∴AD=4,DE=3,
∴AC=…(10分).
31.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.
(1)求证:BE=CM.
(2)求证:AB﹣AC=2BE.
【解答】证明:(1)连接BD,DC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴弧BD=弧CD,
∴BD=CD,
∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,
∵∠M=∠DEB=90°,DE=DM,
在Rt△DEB和Rt△DMC中,
,
∴Rt△DEB≌Rt△DMC(HL),
∴BE=CM.
(2)∵DE⊥AB,DM⊥AC,
∵∠M=∠DEA=90°,
在Rt△DEA和Rt△DMA中
∴Rt△DEA≌Rt△DMA(HL),
∴AE=AM,
∴AB﹣AC,
=AE+BE﹣AC,
=AM+BE﹣AC,
=AC+CM+BE﹣AC,
=BE+CM,
=2BE.
32.(2013?宁夏模拟)如图,OA是⊙0的半径,以OA为直径的⊙C与⊙0的弦AB相交于点D.求证:AD=BD.
【解答】证明:连结OD,如图,
∵OA为⊙C的直径,
∴∠ADO=90°,
∴OD⊥AB,
∴AD=BD.
33.如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
【解答】解:连接OM
∵OD=OM,
∴∠ODM=∠OMD,
∵DM平分∠ODC,
∴∠ODM=∠CDM,
∴∠CDM=∠OMD,
∴CD∥OM,
∵CD⊥AB,
∴OM⊥AB,
∴弧AM=弧BM,
即点M为劣弧AB的中点.
34.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.
【解答】解:连接AE,
∵CE为直径,
∴∠EAC=90°,
∴∠ACE=90°﹣∠AEC,
∵CD是高,D是垂足,
∴∠BCD=90°﹣∠B,
∵∠B=∠AEC(同弧所对的圆周角相等),
∴∠ACE=∠BCD,
∴∠ACE+∠ECD=∠BCD+∠ECD,
∴∠ACD=∠BCE.
35.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
【解答】证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠BAE=90°,
∵AF⊥BC于D,
∴∠FAC+∠ACB=90°,
∵∠E=∠ACB,
∴∠BAE=∠FAC,
∴弧BE=弧CF,
∴BE=CF.
36.已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
【解答】证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠AEB=∠AEC=90°,
∵弦BE=DE,
∴=,
∴∠DAE=∠BAE,
∵∠C=90°﹣∠DAE,∠B=90°﹣∠BAE,
∴∠B=∠C,
∴AC=AB.
37.如图,AB是圆O的直径,OC⊥AB,交⊙O于点C,D是弧AC上一点,E是AB上一点,EC⊥CD,交BD于点F.问:AD与BF相等吗?为什么?
【解答】解:AD和BF相等.理由:如图,
连接AC、BC,
∵OC⊥AB,
∴∠BOC=90°
∴∠BDC=∠BAC=45°
∵EC⊥CD,
∴∠DCE=∠ACB=90°,
∴△DCF和△ACB都是等腰直角三角形,
∴DC=FC,AC=BC,
∵∠DCA+∠ACF=∠BCF+∠ACF=90°,
∴∠DCA=∠FCB
在△ACD和△BCF中,
{,∴△ACD≌△BCF
∴DA=BF.
38.如图,AB是⊙O的直径,AC、DE是⊙O的两条弦,且DE⊥AB,延长AC、DE相交于点F,求证:∠FCD=∠ACE.
【解答】证明:连接AD,AE,
∵AB是直径.AB⊥DE,
∴AB平分DE,弧ACE=弧AD,
∴∠ACD=∠ADE,
∵A、C、E、D四点共圆,
∴∠FCE=∠ADE,
∴∠FCE=∠ACD,
∴∠FCE+∠DCE=∠DAC+∠ECD,
∴∠FCD=∠ACE.
39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.
【解答】解:
延长CE交⊙O于M,
∵AD是⊙O的直径,作CE⊥AD,
∴弧AC=弧AM,
∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).
40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.
【解答】解:△DBC为等腰三角形.理由如下:
∵AD为△ABC的外角平分线,
∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DBC=∠DAC,
∴∠DBC=∠DCB,
∴△DBC为等腰三角形.
一.解答题(共6小题)
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?
【解答】解:∠FGC与∠AGD相等.理由如下:
连接AD,如图,
∵CD⊥AB,
∴=,
∴∠AGD=∠ADC,
∵∠FGC=∠ADC,
∴∠FGC=∠AGD
2.如图,AB是圆O的直径,C是圆O上一点,D是弧AC中点,DE⊥AB垂足为E,AC分别与DE、DB相交于点F、G,则AF与FG是否相等?为什么?
【解答】解:AF=FG,
理由是:连接AD,
∵AB是直径,DE⊥AB,
∴∠ADB=∠DEB=90°,
∴∠ADE=∠ABD,
∵D为弧AC中点,
∴∠DAC=∠ABD,
∴∠ADE=∠DAC,
∴AF=DF,∠FAE=∠DAC,
∴DF=FG,
∴AF=FG.
3.如图,AB为⊙O的直径,以OA为直径作⊙C,AD为⊙O的弦,交⊙C于E,试问,当D点在⊙O上运动时(不与A重合),AE与ED的长度有何关系?证明你的结论.
【解答】解:AE=ED.
理由:连接OE,
∵AO是⊙C的直径,
∴∠OEA=90°,
∴OE⊥AD,
∵OE过圆O的圆心O,
∴AE=ED.
4.如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.
【解答】证明:连接OD,
∵OA为⊙C的直径,
∴∠ODA=90°,即OD⊥AB,
∴D是AB的中点.
5.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;
(2)∠A=∠GEF.
【解答】证明一:
(1)连接DF,∵∠ACB=90°,D是AB的中点,
∴BD=DC=AB,(2分)
∵DC是⊙O的直径,
∴DF⊥BC,(4分)
∴BF=FC,即F是BC的中点;(5分)
(2)∵D,F分别是AB,BC的中点,
∴DF∥AC,(6分)
∴∠A=∠BDF,(7分)
∵∠BDF=∠GEF(圆周角定理),(8分)
∴∠A=∠GEF.(9分)
证明二:
(1)连接DF,DE,
∵DC是⊙O直径,
∴∠DEC=∠DFC=90°.(1分)
∵∠ECF=90°,
∴四边形DECF是矩形.
∴EF=CD,DF=EC.(2分)
∵D是AB的中点,∠ACB=90°,
∴EF=CD=BD=AB.(3分)
∴△DBF≌△EFC.(4分)
∴BF=FC,即F是BC的中点.(5分)
(2)∵△DBF≌△EFC,
∴∠BDF=∠FEC,∠B=∠EFC.(6分)
∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),
∴∠A=∠FEC.(7分)
∵∠FEG=∠BDF(同弧所对的圆周角相等
),(8分)
∴∠A=∠GEF.(9分)
(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)
6.如图,圆内接四边形ABCD的外角∠DCH=∠DCA,DP⊥AC垂足为P,DH⊥BH垂足为H,求证:CH=CP,AP=BH.
【解答】证明:(1)在△DHC与△DPC中,
∵∠DCH=∠DCA,DP⊥AC,DH⊥BH,DC为公共边,
∴△DHC≌△DPC,
∴CH=CP.
(2)连接DB,由圆周角定理得,
∠DAC=∠DBH,
∵△DHC≌△DPC,
∴DH=DP,
∵DP⊥AC,DH⊥BH,
∴∠DHB=∠DPC=90°,
∴△DAP≌△DBH,
∴AP=BH.
第10页(共36页)
同课章节目录
