浙教版七年级上册数学2.5.1有理数的乘方课件(15张)
文档属性
| 名称 | 浙教版七年级上册数学2.5.1有理数的乘方课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 848.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 10:51:41 | ||
图片预览





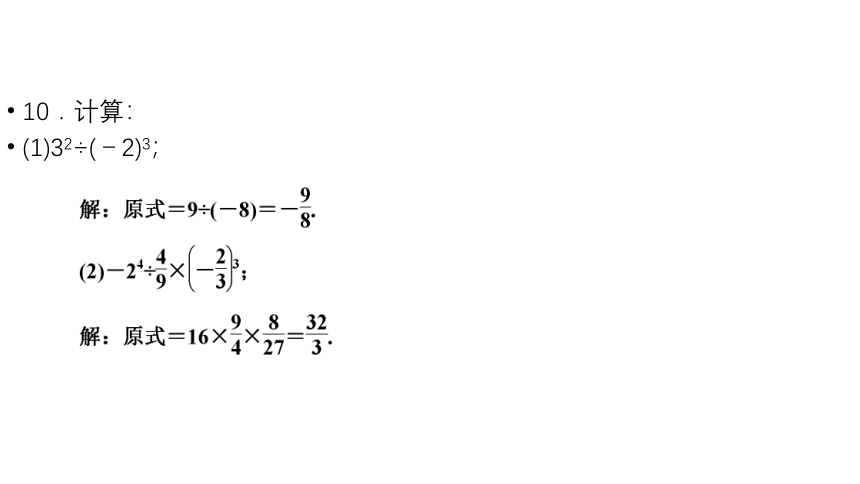
文档简介
第2章 有理数的运算
2.5 有理数的乘方
第一课时 有理数的乘方
*
名 师 点 睛
知识点1 有理数乘方的意义
(1)一般地,在数学上我们把n个相同的因数a相乘的积记做an,即a×a×…×a=an.这种求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂.在an中,a叫做底数,n叫做指数,an读作“a的n次幂”或“a的n次方”.
(2)有理数乘方的符号法则:
①正数的任何次幂是正数,负数的奇数次幂是负数,负数的偶数次幂是正数.
②0的任何正整数次幂是0,00没有意义.
注意:(1)一个数可以看作这个数本身的一次方,如5就是51,指数1通常省略不写.
(2)当幂的底数是负数或分数时,底数应该添上括号.
*
*
基 础 过 关
A
D
*
3.-25的意义是( )
A.2个-5相乘 B.2个-5相加
C.-2乘5 D.25的相反数
4.13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为( )
A.42 B.49
C.76 D.77
D
C
*
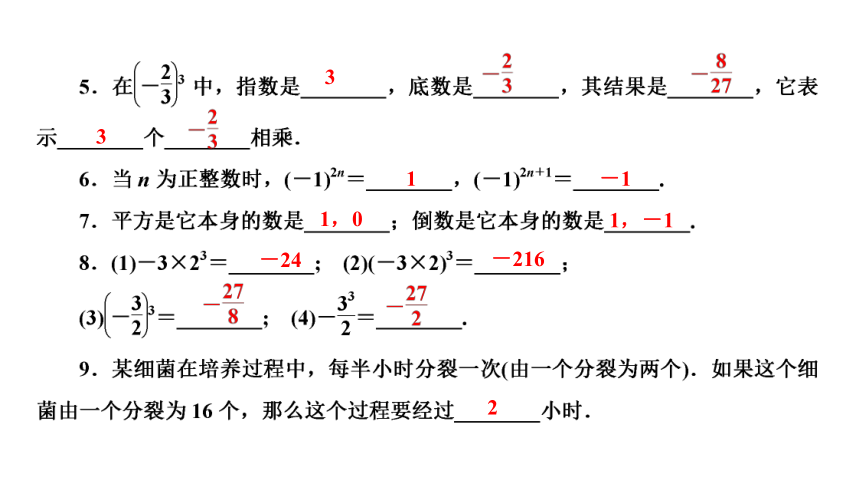
3
3
1
-1
1,0
1,-1
-24
-216
2
*
10.计算:
(1)32÷(-2)3;
*
*
能 力 提 升
11.你吃过“拉面”吗?如果把一个面团拉开,然后对折,再拉开,再对折,如此反复做下去,对折10次拉出的面条是( )
A.20根 B.10根
C.100根 D.1024根
D
*
12.定义一种新的运算:a&b=ab,如2&3=23=8,那么(3&2)&2=________.
13.已知(3-m)2+|n+2|=0,则nm=________.
14.观察下列等式:
13=12;
13+23=32;
13+23+33=62;
13+23+33+43=102;
……
想一想,等式左边各次幂的底数与右边幂的底数有什么关系,猜一猜可以得到什么规律,再把这个规律用等式写出来:___________________________________.
81
-8
13+23+33+…+n3=(1+2+3+…+n)2
*
*
*
*
18.阅读材料:
我们平常用的是十进制,如1967=1×103+9×102+6×101+7,表示十进制的数要用10个数码:0,1,2,3,4,5,6,7,8,9.在计算机中用的是二进制,只有两个数码:0,1,如二进制中111=1×22+1×21+1相当于十进制中的7,11011=1×24+1×23+0×22+1×21+1相当于十进制中的27.
根据上述材料,解答下列问题:
(1)二进制中的1011相当于十进制中的多少?
(2)二进制中的什么数相当于十进制中的8?
解:(1)1011=1×23+0×22+1×21+1=11,即二进制中的1011相当于十进制中的11.
(2)8=23=0+0×21+0×22+1×23,即二进制中的1000相当于十进制中的8.
*
思 维 训 练
19.观察下列各式:
(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4,….
解答问题:
(1)验证:(4×0.25)100=________,4100×0.25100=________;
(2)通过上述验证,归纳得出:(ab)n=________,(abc)n=________;
(3)请运用上述性质计算:(-0.125)2019×22018×42018.
解:原式=(-0.125)2018×22018×42018×(-0.125)=(-0.125×2×4)2018×(-0.125)=(-1)2018×(-0.125)=1×(-0.125)=-0.125.
1
1
anbn
anbncn
2.5 有理数的乘方
第一课时 有理数的乘方
*
名 师 点 睛
知识点1 有理数乘方的意义
(1)一般地,在数学上我们把n个相同的因数a相乘的积记做an,即a×a×…×a=an.这种求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂.在an中,a叫做底数,n叫做指数,an读作“a的n次幂”或“a的n次方”.
(2)有理数乘方的符号法则:
①正数的任何次幂是正数,负数的奇数次幂是负数,负数的偶数次幂是正数.
②0的任何正整数次幂是0,00没有意义.
注意:(1)一个数可以看作这个数本身的一次方,如5就是51,指数1通常省略不写.
(2)当幂的底数是负数或分数时,底数应该添上括号.
*
*
基 础 过 关
A
D
*
3.-25的意义是( )
A.2个-5相乘 B.2个-5相加
C.-2乘5 D.25的相反数
4.13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为( )
A.42 B.49
C.76 D.77
D
C
*
3
3
1
-1
1,0
1,-1
-24
-216
2
*
10.计算:
(1)32÷(-2)3;
*
*
能 力 提 升
11.你吃过“拉面”吗?如果把一个面团拉开,然后对折,再拉开,再对折,如此反复做下去,对折10次拉出的面条是( )
A.20根 B.10根
C.100根 D.1024根
D
*
12.定义一种新的运算:a&b=ab,如2&3=23=8,那么(3&2)&2=________.
13.已知(3-m)2+|n+2|=0,则nm=________.
14.观察下列等式:
13=12;
13+23=32;
13+23+33=62;
13+23+33+43=102;
……
想一想,等式左边各次幂的底数与右边幂的底数有什么关系,猜一猜可以得到什么规律,再把这个规律用等式写出来:___________________________________.
81
-8
13+23+33+…+n3=(1+2+3+…+n)2
*
*
*
*
18.阅读材料:
我们平常用的是十进制,如1967=1×103+9×102+6×101+7,表示十进制的数要用10个数码:0,1,2,3,4,5,6,7,8,9.在计算机中用的是二进制,只有两个数码:0,1,如二进制中111=1×22+1×21+1相当于十进制中的7,11011=1×24+1×23+0×22+1×21+1相当于十进制中的27.
根据上述材料,解答下列问题:
(1)二进制中的1011相当于十进制中的多少?
(2)二进制中的什么数相当于十进制中的8?
解:(1)1011=1×23+0×22+1×21+1=11,即二进制中的1011相当于十进制中的11.
(2)8=23=0+0×21+0×22+1×23,即二进制中的1000相当于十进制中的8.
*
思 维 训 练
19.观察下列各式:
(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4,….
解答问题:
(1)验证:(4×0.25)100=________,4100×0.25100=________;
(2)通过上述验证,归纳得出:(ab)n=________,(abc)n=________;
(3)请运用上述性质计算:(-0.125)2019×22018×42018.
解:原式=(-0.125)2018×22018×42018×(-0.125)=(-0.125×2×4)2018×(-0.125)=(-1)2018×(-0.125)=1×(-0.125)=-0.125.
1
1
anbn
anbncn
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
