2020-2021学年浙教版八年级数学第一章《三角形的初步认识》综合提高B卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级数学第一章《三角形的初步认识》综合提高B卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 12:54:46 | ||
图片预览


文档简介
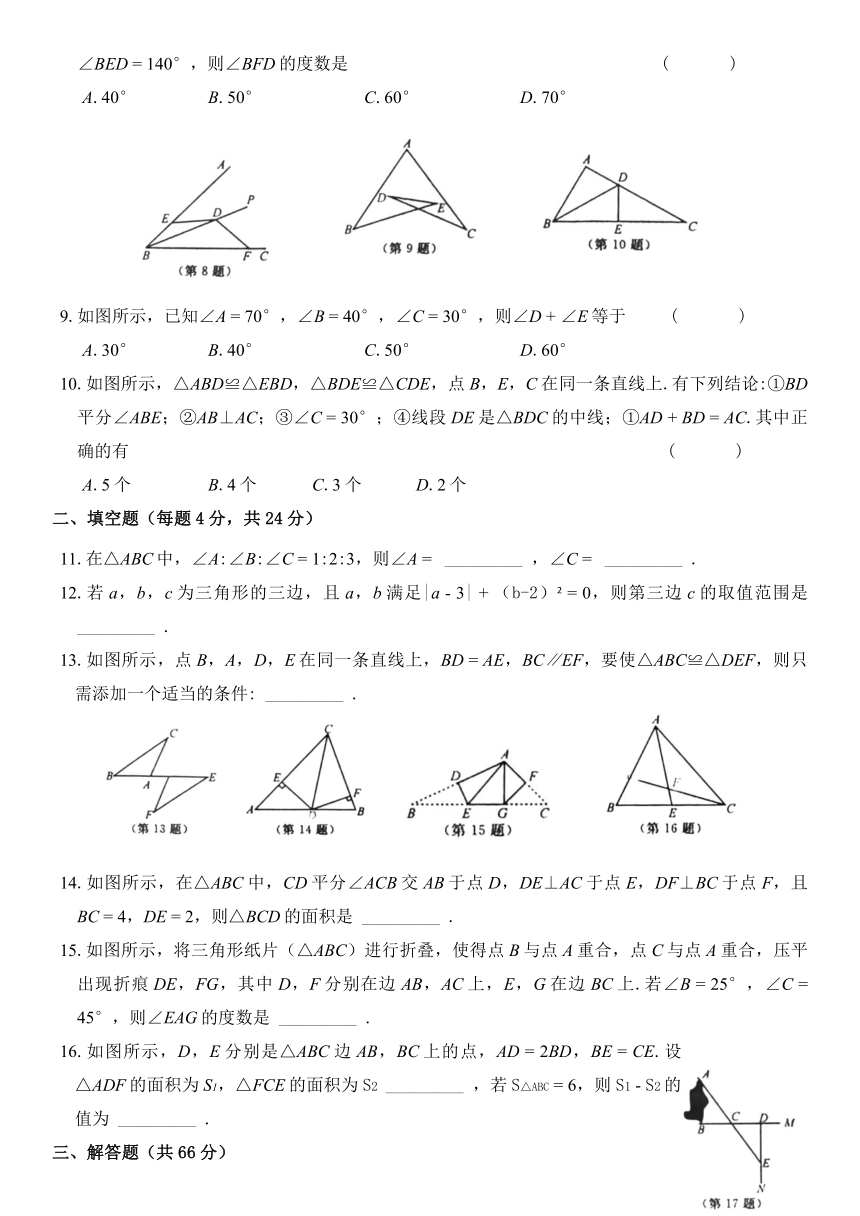
2020-2021学年浙教版八年级数学第一章《三角形的初步认识》综合提高B卷
姓名
班级
一、选择题(每题3分,共30分)
1.下列各组数中,可能是一个三角形的边长的为
(
)
A.1,2,4
B.4,5,9
C.4,6,8
D.5,5,11
2.如图所示,将三角尺的直角顶点放在直尺的一边上,∠1
=
30°,∠2
=
50°,则∠3的度数为
(
)
A.50°
B.30°
C.20°
D.15°
3.如图所示,已知△ABC(AC
<
AB
<
BC),用尺规在线段BC上确定一点P,使得PA
+
PC
=
BC,则符合要求的作图痕迹是
(
)
4.如图所示,△ABC≌△AEF,AB
=
AE,∠B
=
∠E.下列结论中,不正确的是
(
)
A.∠EAB
=
∠FAC
B.BC
=
EF
C.∠BAC
=
∠CAF
D.∠AFE
=
∠ACB
5.下列说法中,正确的是
(
)
A.有两边及一角对应相等的两个三角形全等
B.三角形中至少有一个内角不小于60°
C.直角三角形仅有一条高线
D.三角形的任意一个外角都大于任何一个内角
6.如图所示,在由若干个正六边形拼成的图形中,下列三角形与△ACD全等的有(
)
A.△BCE
B.△ADF
C.△ADE
D.△CDE
7.如图所示,已知D,E分别是△ABC的边BC,AC上的中点,连结DE,AD.若S△ABC
=
24
cm2,则△DEC的面积为
(
)
A.24
cm2
B.6
cm2
C.8
cm2
D.12
cm2
8.如图所示,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE
=
DF.若∠BED
=
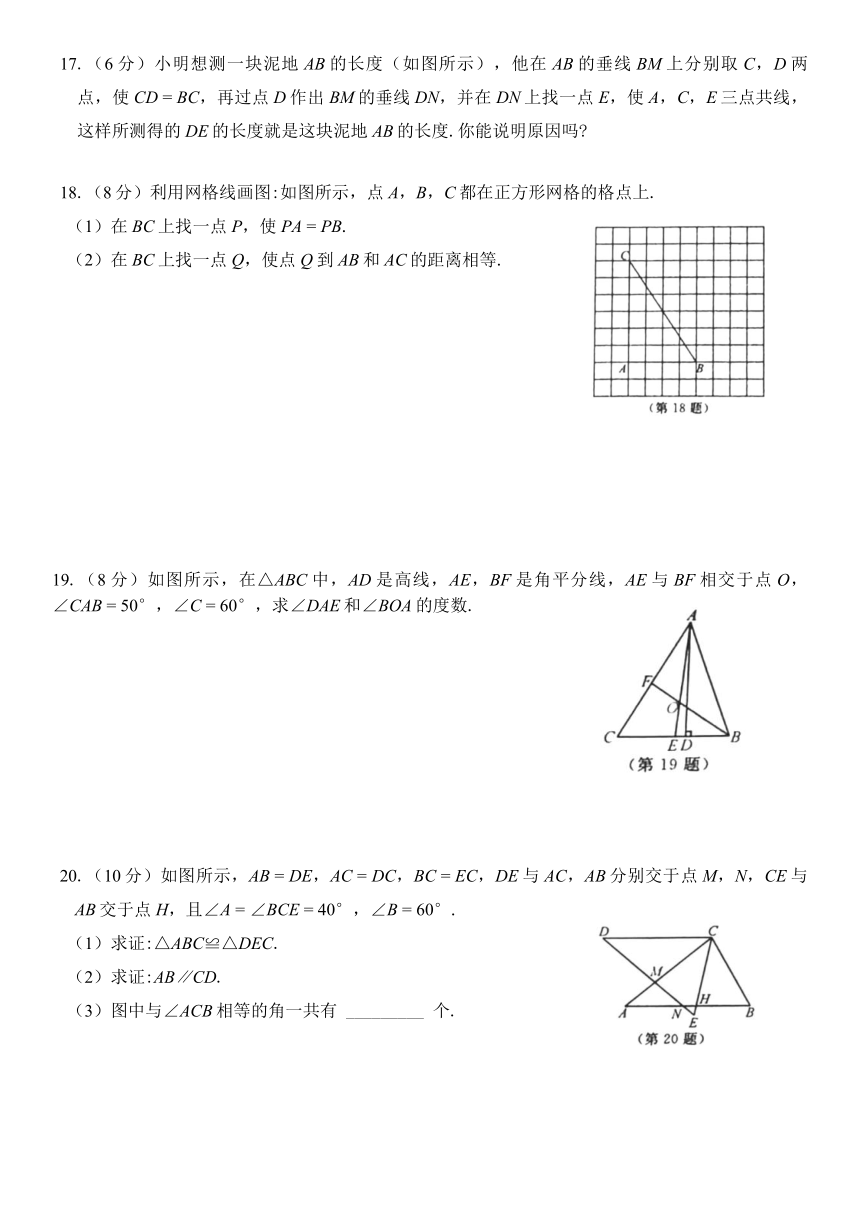
140°,则∠BFD的度数是
(
)
A.40°
B.50°
C.60°
D.70°
9.如图所示,已知∠A
=
70°,∠B
=
40°,∠C
=
30°,则∠D
+
∠E等于
(
)
A.30°
B.40°
C.50°
D.60°
10.如图所示,△ABD≌△EBD,△BDE≌△CDE,点B,E,C在同一条直线上.有下列结论:①BD平分∠ABE;②AB⊥AC;③∠C
=
30°;④线段DE是△BDC的中线;①AD
+
BD
=
AC.其中正确的有
(
)
A.5个
B.4个
C.3个
D.2个
二、填空题(每题4分,共24分)
11.在△ABC中,∠A:∠B:∠C
=
1:2:3,则∠A
=
_________
,∠C
=
_________
.
12.若a,b,c为三角形的三边,且a,b满足|a
-
3|
+
(b-2)2
=
0,则第三边c的取值范围是
_________
.
13.如图所示,点B,A,D,E在同一条直线上,BD
=
AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件:
_________
.
14.如图所示,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC于点E,DF⊥BC于点F,且BC
=
4,DE
=
2,则△BCD的面积是
_________
.
15.如图所示,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上.若∠B
=
25°,∠C
=
45°,则∠EAG的度数是
_________
.
16.如图所示,D,E分别是△ABC边AB,BC上的点,AD
=
2BD,BE
=
CE.设△ADF的面积为S1,△FCE的面积为S2
_________
,若S△ABC
=
6,则S1
-
S2的值为
_________
.
三、解答题(共66分)
17.(6分)小明想测一块泥地AB的长度(如图所示),他在AB的垂线BM上分别取C,D两点,使CD
=
BC,再过点D作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这样所测得的DE的长度就是这块泥地AB的长度.你能说明原因吗?
18.(8分)利用网格线画图:如图所示,点A,B,C都在正方形网格的格点上.
(1)在BC上找一点P,使PA
=
PB.
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.
19.(8分)如图所示,在△ABC中,AD是高线,AE,BF是角平分线,AE与BF相交于点O,∠CAB
=
50°,∠C
=
60°,求∠DAE和∠BOA的度数.
20.(10分)如图所示,AB
=
DE,AC
=
DC,BC
=
EC,DE与AC,AB分别交于点M,N,CE与AB交于点H,且∠A
=
∠BCE
=
40°,∠B
=
60°.
(1)求证:△ABC≌△DEC.
(2)求证:AB∥CD.
(3)图中与∠ACB相等的角一共有
_________
个.
21.(10分)如图所示,BM,CN是△ABC的高线,点P在直线BM上,点Q在直线CN上,且BP
=
AC,CQ
=
AB.
(1)猜想AQ与AP的大小关系,并证明你的结论.
(2)判断AQ与AP有何特殊的位置关系,并证明你的结论.
22.(12分)已知△ABC中,BE平分∠ABC,点P在射线BE上.
(1)如图1所示,若∠ABC
=
40°,CP∥AB,求∠BPC的度数.
(2)如图2所示,若∠BAC
=
100°,∠PBC
=
∠PCA,求∠BPC的度数.
(3)若∠ABC
=
40°,∠ACB
=
30°,直线CP与△ABC的一条边垂直,求∠BPC的度数.
23.(12分)在△ABC中,∠B
=
60°,D,E分别为AB,BC上的点,且AE,CD交于点F.
(1)如图1所示,已知AE,CD为△ABC的角平分线.
①求证:∠AFC
=
120°.
②若AD
=
6,CE
=
4,求AC的长.
(2)如图2所示,若∠FAC
=
∠FCA
=
30°,求证:AD
=
CE.
姓名
班级
一、选择题(每题3分,共30分)
1.下列各组数中,可能是一个三角形的边长的为
(
)
A.1,2,4
B.4,5,9
C.4,6,8
D.5,5,11
2.如图所示,将三角尺的直角顶点放在直尺的一边上,∠1
=
30°,∠2
=
50°,则∠3的度数为
(
)
A.50°
B.30°
C.20°
D.15°
3.如图所示,已知△ABC(AC
<
AB
<
BC),用尺规在线段BC上确定一点P,使得PA
+
PC
=
BC,则符合要求的作图痕迹是
(
)
4.如图所示,△ABC≌△AEF,AB
=
AE,∠B
=
∠E.下列结论中,不正确的是
(
)
A.∠EAB
=
∠FAC
B.BC
=
EF
C.∠BAC
=
∠CAF
D.∠AFE
=
∠ACB
5.下列说法中,正确的是
(
)
A.有两边及一角对应相等的两个三角形全等
B.三角形中至少有一个内角不小于60°
C.直角三角形仅有一条高线
D.三角形的任意一个外角都大于任何一个内角
6.如图所示,在由若干个正六边形拼成的图形中,下列三角形与△ACD全等的有(
)
A.△BCE
B.△ADF
C.△ADE
D.△CDE
7.如图所示,已知D,E分别是△ABC的边BC,AC上的中点,连结DE,AD.若S△ABC
=
24
cm2,则△DEC的面积为
(
)
A.24
cm2
B.6
cm2
C.8
cm2
D.12
cm2
8.如图所示,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE
=
DF.若∠BED
=
140°,则∠BFD的度数是
(
)
A.40°
B.50°
C.60°
D.70°
9.如图所示,已知∠A
=
70°,∠B
=
40°,∠C
=
30°,则∠D
+
∠E等于
(
)
A.30°
B.40°
C.50°
D.60°
10.如图所示,△ABD≌△EBD,△BDE≌△CDE,点B,E,C在同一条直线上.有下列结论:①BD平分∠ABE;②AB⊥AC;③∠C
=
30°;④线段DE是△BDC的中线;①AD
+
BD
=
AC.其中正确的有
(
)
A.5个
B.4个
C.3个
D.2个
二、填空题(每题4分,共24分)
11.在△ABC中,∠A:∠B:∠C
=
1:2:3,则∠A
=
_________
,∠C
=
_________
.
12.若a,b,c为三角形的三边,且a,b满足|a
-
3|
+
(b-2)2
=
0,则第三边c的取值范围是
_________
.
13.如图所示,点B,A,D,E在同一条直线上,BD
=
AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件:
_________
.
14.如图所示,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC于点E,DF⊥BC于点F,且BC
=
4,DE
=
2,则△BCD的面积是
_________
.
15.如图所示,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上.若∠B
=
25°,∠C
=
45°,则∠EAG的度数是
_________
.
16.如图所示,D,E分别是△ABC边AB,BC上的点,AD
=
2BD,BE
=
CE.设△ADF的面积为S1,△FCE的面积为S2
_________
,若S△ABC
=
6,则S1
-
S2的值为
_________
.
三、解答题(共66分)
17.(6分)小明想测一块泥地AB的长度(如图所示),他在AB的垂线BM上分别取C,D两点,使CD
=
BC,再过点D作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这样所测得的DE的长度就是这块泥地AB的长度.你能说明原因吗?
18.(8分)利用网格线画图:如图所示,点A,B,C都在正方形网格的格点上.
(1)在BC上找一点P,使PA
=
PB.
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.
19.(8分)如图所示,在△ABC中,AD是高线,AE,BF是角平分线,AE与BF相交于点O,∠CAB
=
50°,∠C
=
60°,求∠DAE和∠BOA的度数.
20.(10分)如图所示,AB
=
DE,AC
=
DC,BC
=
EC,DE与AC,AB分别交于点M,N,CE与AB交于点H,且∠A
=
∠BCE
=
40°,∠B
=
60°.
(1)求证:△ABC≌△DEC.
(2)求证:AB∥CD.
(3)图中与∠ACB相等的角一共有
_________
个.
21.(10分)如图所示,BM,CN是△ABC的高线,点P在直线BM上,点Q在直线CN上,且BP
=
AC,CQ
=
AB.
(1)猜想AQ与AP的大小关系,并证明你的结论.
(2)判断AQ与AP有何特殊的位置关系,并证明你的结论.
22.(12分)已知△ABC中,BE平分∠ABC,点P在射线BE上.
(1)如图1所示,若∠ABC
=
40°,CP∥AB,求∠BPC的度数.
(2)如图2所示,若∠BAC
=
100°,∠PBC
=
∠PCA,求∠BPC的度数.
(3)若∠ABC
=
40°,∠ACB
=
30°,直线CP与△ABC的一条边垂直,求∠BPC的度数.
23.(12分)在△ABC中,∠B
=
60°,D,E分别为AB,BC上的点,且AE,CD交于点F.
(1)如图1所示,已知AE,CD为△ABC的角平分线.
①求证:∠AFC
=
120°.
②若AD
=
6,CE
=
4,求AC的长.
(2)如图2所示,若∠FAC
=
∠FCA
=
30°,求证:AD
=
CE.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
