初中数学浙教版九年级上册3.3垂径定理同步练习(Word版 含解析)
文档属性
| 名称 | 初中数学浙教版九年级上册3.3垂径定理同步练习(Word版 含解析) | 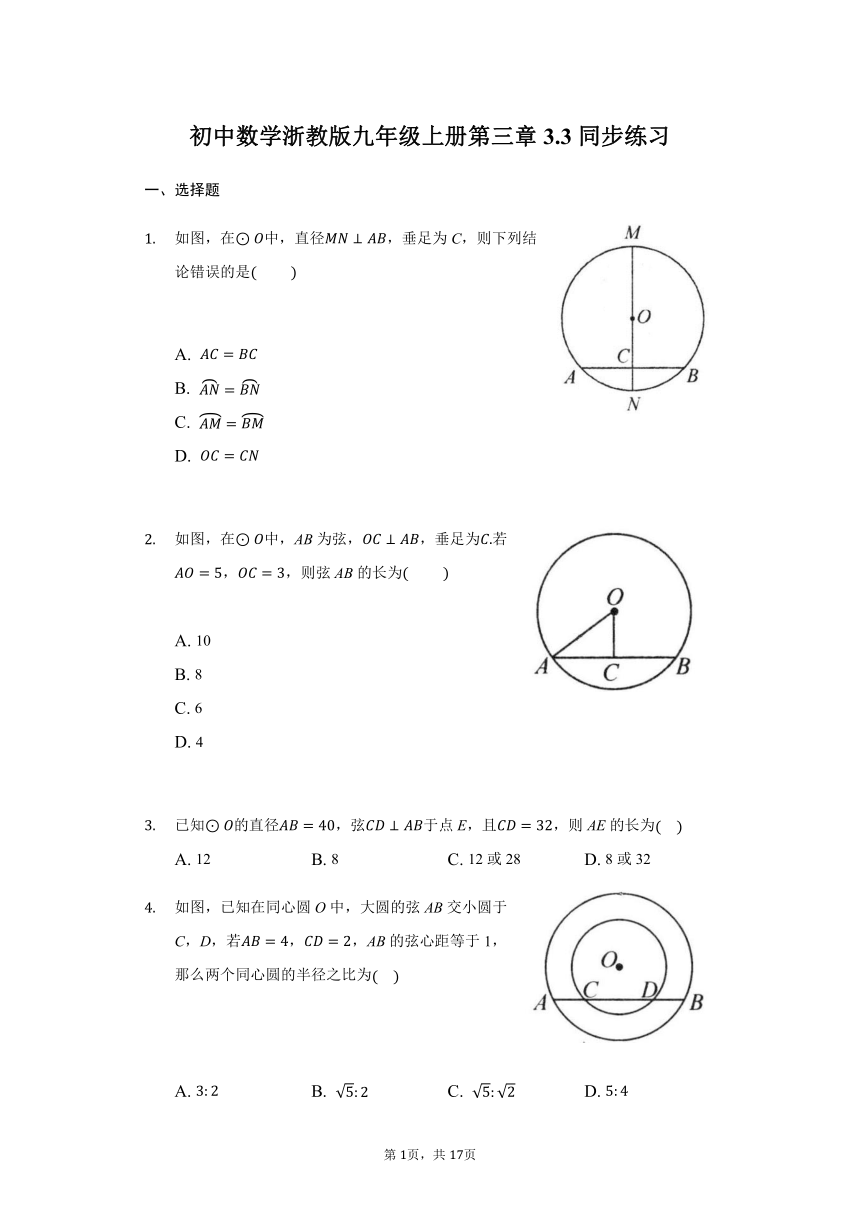 | |
| 格式 | docx | ||
| 文件大小 | 353.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 15:26:26 | ||
图片预览




文档简介
初中数学浙教版九年级上册第三章3.3同步练习
一、选择题
如图,在中,直径,垂足为C,则下列结论错误的是?
?
?
A.
B.
C.
D.
如图,在中,AB为弦,,垂足为若,,则弦AB的长为?
?
?
A.
10
B.
8
C.
6
D.
4
已知的直径,弦于点E,且,则AE的长为
A.
12
B.
8
C.
12或28
D.
8或32
如图,已知在同心圆O中,大圆的弦AB交小圆于C,D,若,,AB的弦心距等于1,那么两个同心圆的半径之比为
A.
B.
C.
D.
如图,圆弧形桥拱的跨度,拱高,则拱桥的半径为
A.
B.
9m
C.
13m
D.
15m
如图,在中,AB是弦,,垂足为C,若,,则的半径OA等于?
?
?
A.
16
B.
12
C.
10
D.
8
如图所示,AB为的直径,弦于点E,若,,则CD等于
A.
5
B.
8
C.
D.
如图所示,已知的半径为10,弦,M是AB上任意一点,则线段OM的长可能是
A.
5
B.
7
C.
9
D.
11
一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽,最深处水深,则此输水管道横截面的直径是
A.
B.
1m
C.
2m
D.
4m
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是中弦CD的中点,EM经过圆心O交于点若,则隧道的高的长为
A.
4
B.
6
C.
8
D.
9
二、填空题
半径为5的内有一点P,且,则过点P的最长的弦长是??????????,最短的弦长是??????????.
如图,的半径,设,P为AB上一动点,则点P到圆心O的最短距离为??????????cm.
已知的半径为5,弦,,,则四边形ABDC的面积为??????????.
若点P是半径为5的内一点,且,在过点P的所有的弦中,弦长为整数的弦有??????????条
如图是一个水平放置的圆柱形水管的横截面,已知水面高,水面宽AB为48cm,那么水管横截面圆的半径是??????????cm.
三、解答题
如图,经过原点,平行于y轴的直线交圆于B,C两点已知点B的坐标是,求A和C的坐标.
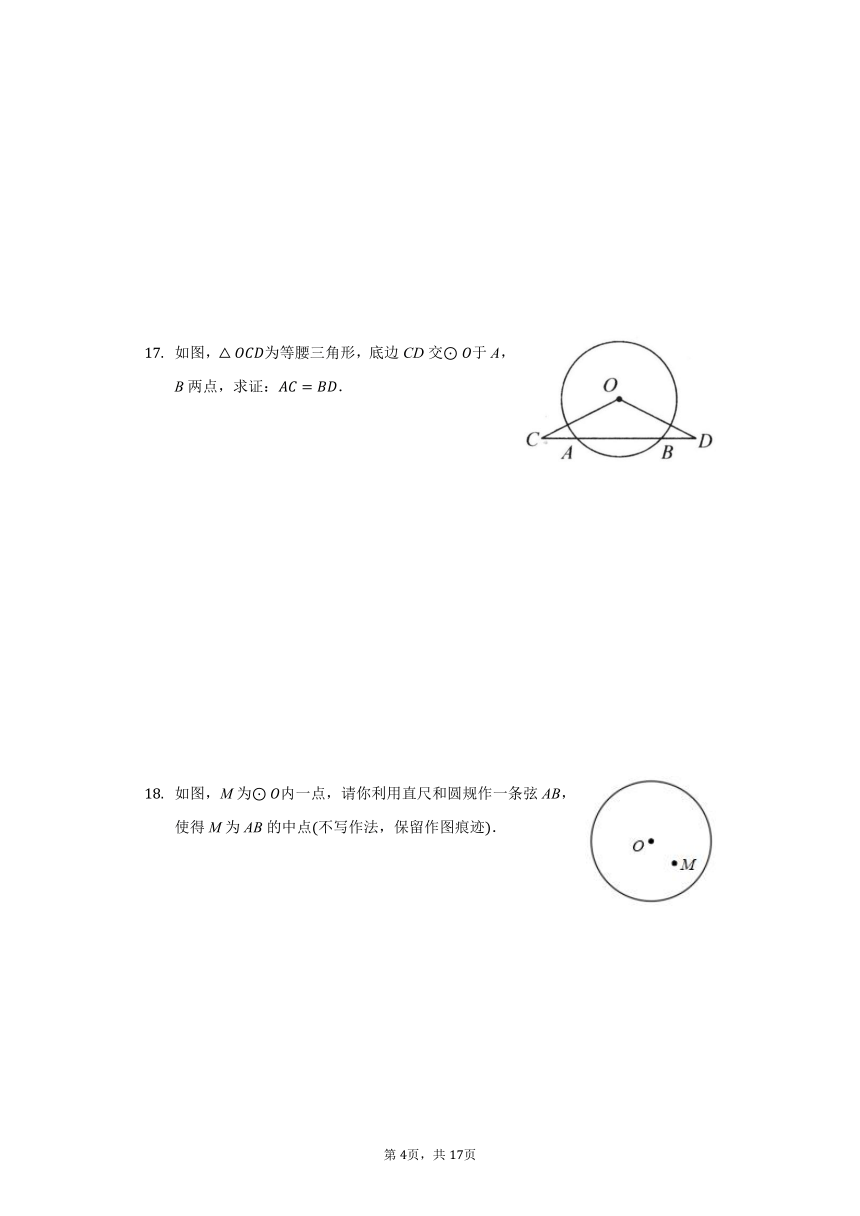
如图,为等腰三角形,底边CD交于A,B两点,求证:.
如图,M为内一点,请你利用直尺和圆规作一条弦AB,使得M为AB的中点不写作法,保留作图痕迹.
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查的是对垂径定理的记忆与理解,掌握垂径定理内容即:垂直于弦的直径,平分弦,且平分弦所对的劣弧,平分弦所对的优弧并能够灵活运用是解题关键.
【解答】
解:根据MN为的直径,且,垂足为C,
则MN是垂直于弦AB的直径,满足垂径定理.因而:
A.是垂径定理的结论,该选项正确;
B.是垂径定理的结论,该选项正确;
C.是垂径定理的结论,该选项正确;
D.不是垂径定理的结论,该选项错误.
故选:D.
2.【答案】B
【解析】
【分析】
此题主要考查的是勾股定理及垂径定理的应用.
在中,根据勾股定理易求得AC的长;由垂径定理知,由此可求得AB的值.
【解答】
解:中,,,
根据勾股定理,得,
所以,
故选B.
3.【答案】D
【解析】
【分析】
本题主要考查了垂径定理,勾股定理,正确理解应分两种情况讨论是解题关键.在直角中,利用勾股定理即可求得OE的长,则或,据此即可求解.
【解答】
解:如图,连接OC,
弦于点E
,
在直角中,,
则,
或,
故AE的长是8或32.
故选D.
4.【答案】C
【解析】
【分析】
本题考查垂径定理,勾股定理,首先过O作于E,连接OC,OA,则OA为大圆半径,OC为小圆半径,而弦心距OE等于1,根据垂径定理结合AB,CD的长可知,,分别用勾股定理求出中OA的长度,再求出中OC的长度,进而可求出本题结果.
【解答】
解:过O作于E,连接OC,OA,如图:
的弦心距等于1
,
在中,
在中,
即两个同心圆的半径之比为:
故选C.
5.【答案】A
【解析】
【分析】
本题考查了垂径定理的应用,熟练掌握勾股定理的性质,能够运用到实际生活当中.由圆弧先假设一圆心,跨度为已知量,设圆心半径为R,桥拱高,则可利用勾股定理在中求解.
【解答】
解:设圆心为O,圆心半径为R,连接AO、OD,
由题中已知条件可得,
,,,
,
,
,
故选A.
6.【答案】C
【解析】
【分析】
本题是垂径定理和勾股定理的运用,属简单题目.本题用垂径定理和勾股定理即可解答.
【解答】
解:如图,连接OA.
在中,AB是弦,,垂足为C,,,
.
在中,,,
,
故选C.
7.【答案】B
【解析】
【分析】
本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
连接OD,先根据垂径定理得出,再由,求出的半径,根据勾股定理求出DE的长,进而可得出结论.
【解答】
解:连接OD,
为的直径,弦于点E,
.
,,
的半径,
,
在中,
,,
,
.
故选B.
8.【答案】C
【解析】
【分析】
本题主要考查了垂径定理解决与弦有关的问题,一般是构造直角三角形,利用勾股定理解题由题意知,OM的最大值是10,弦AB的弦心距是OM的最小值,利用垂径定理和勾股定理,可求出OM的最小值为8,因而答案中只有9符合条件?
【解答】
解:过点O作,垂足为M,
,,
,
在中,,
所以.
故应选C.
9.【答案】B
【解析】
【分析】
?本题考查的是垂径定理,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.根据题意知,已知弦长和弓形高,求半径直径,根据垂径定理和勾股定理求解即可.
【解答】
解:如图,设半径为r,过O作交AB于点D,连接OA、OB,则米,
设,则,
在中,
,即,
解得米,
故此输水管道的直径米.
故选B.
10.【答案】D
【解析】解:是弦CD的中点,
根据垂径定理:,
又则有:,
设OM是x米,
在中,有,
即:,
解得:,
所以.
故选D.
因为M是弦CD的中点,根据垂径定理,,则,在中,有,可求得OM,进而就可求得EM.
此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
11.【答案】10,6
【解析】
【分析】
本题结合勾股定理考查了垂径定理,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
过点P的最长弦就是直径,最短弦就是垂直于OP的弦,根据垂径定理和勾股定理可求得.
【解答】
解:
过点P的最长弦就是直径,,
最短弦就是垂直于OP的弦,
如图所示,于P,
,,
,
弦.
故答案为:10,6.
12.【答案】6
【解析】
【分析】
本题利用了垂线段最短和垂径定理及勾股定理求解.根据垂线段最短,可以得到当时,点P到圆心O的距离最短.根据垂径定理和勾股定理即可求解.
【解答】
解:根据垂线段最短知,
当点P运动到时,点P到到点O的距离最短,
由垂径定理知,此时点P为AB中点,,
由勾股定理得,此时,
故答案为6.
13.【答案】49或7
【解析】
【分析】
本题考查了勾股定理和垂径定理,解答此题时要注意进行分类讨论,不要漏解.
由于弦AB、CD的具体位置不能确定,故应分两种情况进行讨论:弦AB和CD在圆心同侧;弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
【解答】
解:当弦AB和CD在圆心同侧时,如图,
过点O作,垂足为F,交AB于点E,连接OA,OC,
,
,
,,
,,
,
由勾股定理得:,,
则四边形ABDC的面积为:
当弦AB和CD在圆心异侧时,如图,
过点O作于点E,反向延长OE交CD于点F,连接OA,OC,
同理可得,,,
,
则四边形ABDC的面积为:
则四边形ABDC的面积为7或49.
故答案为49或7.
14.【答案】4
【解析】
【分析】
此题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧,勾股定理.由,则AB是过P的最短的弦,过P的最长的弦是圆的直径,首先根据垂径定理和勾股定理可以求出AB的长度,然后结合已知条件就可以求出弦长为整数的弦的条数.
【解答】
解:如图,
CD为过P点的直径,AB是与OP垂直的弦,连OA,
则过点P的所有的弦中CD最长,AB最短,并且,
,
,
在中
,,
,
,
过点P的弦中弦长可以为整数9,由圆的对称性得到弦长为9的弦有两条,
在过点P的所有的弦中,弦长为整数的弦的条数共有4条,
故答案为4.
15.【答案】26
【解析】
【分析】
本题主要考查了垂径定理和勾股定理,作出恰当的辅助线,利用定理是解答此题的关键.连接OA,根据垂径定理得,根据勾股定理即刻得到结论.
【解答】
解:连接OA,
,
,
在中,,
即,
,
水管横截面圆的半径是26cm,
故答案为26.
16.【答案】解:过A作于N,连接AB,
设的半径为R,则,
点B的坐标是,
,,
在中,由勾股定理得:,
即,
解得:,
,
点的坐标是,,
,AO过圆心A,
,
即,
,
点的坐标是.
【解析】本题考查了坐标与图形的性质,勾股定理,垂径定理等知识点,能求出半径AO的长是解此题的关键.根据勾股定理求出OA,求出BN,根据垂径定理求出,即可求出答案.
17.【答案】证明:过点O作,
,
,
又在中,
,
.
【解析】
【分析】本题考查的是垂径定理,根据题意作出辅助线,利用垂径定理求解是解答此题的关键.
过点O作,由等腰三角形的性质可知,再由垂径定理可知AE,故可得出结论.
18.【答案】解:如图,弦AB即为所求.
【解析】作直线OM,过点M作直线交于A,B,弦AB即为所求.
本题考查垂径定理,解题的关键是理解题意,灵活运用所学知识解决问题.
第2页,共2页
第1页,共1页
一、选择题
如图,在中,直径,垂足为C,则下列结论错误的是?
?
?
A.
B.
C.
D.
如图,在中,AB为弦,,垂足为若,,则弦AB的长为?
?
?
A.
10
B.
8
C.
6
D.
4
已知的直径,弦于点E,且,则AE的长为
A.
12
B.
8
C.
12或28
D.
8或32
如图,已知在同心圆O中,大圆的弦AB交小圆于C,D,若,,AB的弦心距等于1,那么两个同心圆的半径之比为
A.
B.
C.
D.
如图,圆弧形桥拱的跨度,拱高,则拱桥的半径为
A.
B.
9m
C.
13m
D.
15m
如图,在中,AB是弦,,垂足为C,若,,则的半径OA等于?
?
?
A.
16
B.
12
C.
10
D.
8
如图所示,AB为的直径,弦于点E,若,,则CD等于
A.
5
B.
8
C.
D.
如图所示,已知的半径为10,弦,M是AB上任意一点,则线段OM的长可能是
A.
5
B.
7
C.
9
D.
11
一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽,最深处水深,则此输水管道横截面的直径是
A.
B.
1m
C.
2m
D.
4m
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是中弦CD的中点,EM经过圆心O交于点若,则隧道的高的长为
A.
4
B.
6
C.
8
D.
9
二、填空题
半径为5的内有一点P,且,则过点P的最长的弦长是??????????,最短的弦长是??????????.
如图,的半径,设,P为AB上一动点,则点P到圆心O的最短距离为??????????cm.
已知的半径为5,弦,,,则四边形ABDC的面积为??????????.
若点P是半径为5的内一点,且,在过点P的所有的弦中,弦长为整数的弦有??????????条
如图是一个水平放置的圆柱形水管的横截面,已知水面高,水面宽AB为48cm,那么水管横截面圆的半径是??????????cm.
三、解答题
如图,经过原点,平行于y轴的直线交圆于B,C两点已知点B的坐标是,求A和C的坐标.
如图,为等腰三角形,底边CD交于A,B两点,求证:.
如图,M为内一点,请你利用直尺和圆规作一条弦AB,使得M为AB的中点不写作法,保留作图痕迹.
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查的是对垂径定理的记忆与理解,掌握垂径定理内容即:垂直于弦的直径,平分弦,且平分弦所对的劣弧,平分弦所对的优弧并能够灵活运用是解题关键.
【解答】
解:根据MN为的直径,且,垂足为C,
则MN是垂直于弦AB的直径,满足垂径定理.因而:
A.是垂径定理的结论,该选项正确;
B.是垂径定理的结论,该选项正确;
C.是垂径定理的结论,该选项正确;
D.不是垂径定理的结论,该选项错误.
故选:D.
2.【答案】B
【解析】
【分析】
此题主要考查的是勾股定理及垂径定理的应用.
在中,根据勾股定理易求得AC的长;由垂径定理知,由此可求得AB的值.
【解答】
解:中,,,
根据勾股定理,得,
所以,
故选B.
3.【答案】D
【解析】
【分析】
本题主要考查了垂径定理,勾股定理,正确理解应分两种情况讨论是解题关键.在直角中,利用勾股定理即可求得OE的长,则或,据此即可求解.
【解答】
解:如图,连接OC,
弦于点E
,
在直角中,,
则,
或,
故AE的长是8或32.
故选D.
4.【答案】C
【解析】
【分析】
本题考查垂径定理,勾股定理,首先过O作于E,连接OC,OA,则OA为大圆半径,OC为小圆半径,而弦心距OE等于1,根据垂径定理结合AB,CD的长可知,,分别用勾股定理求出中OA的长度,再求出中OC的长度,进而可求出本题结果.
【解答】
解:过O作于E,连接OC,OA,如图:
的弦心距等于1
,
在中,
在中,
即两个同心圆的半径之比为:
故选C.
5.【答案】A
【解析】
【分析】
本题考查了垂径定理的应用,熟练掌握勾股定理的性质,能够运用到实际生活当中.由圆弧先假设一圆心,跨度为已知量,设圆心半径为R,桥拱高,则可利用勾股定理在中求解.
【解答】
解:设圆心为O,圆心半径为R,连接AO、OD,
由题中已知条件可得,
,,,
,
,
,
故选A.
6.【答案】C
【解析】
【分析】
本题是垂径定理和勾股定理的运用,属简单题目.本题用垂径定理和勾股定理即可解答.
【解答】
解:如图,连接OA.
在中,AB是弦,,垂足为C,,,
.
在中,,,
,
故选C.
7.【答案】B
【解析】
【分析】
本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
连接OD,先根据垂径定理得出,再由,求出的半径,根据勾股定理求出DE的长,进而可得出结论.
【解答】
解:连接OD,
为的直径,弦于点E,
.
,,
的半径,
,
在中,
,,
,
.
故选B.
8.【答案】C
【解析】
【分析】
本题主要考查了垂径定理解决与弦有关的问题,一般是构造直角三角形,利用勾股定理解题由题意知,OM的最大值是10,弦AB的弦心距是OM的最小值,利用垂径定理和勾股定理,可求出OM的最小值为8,因而答案中只有9符合条件?
【解答】
解:过点O作,垂足为M,
,,
,
在中,,
所以.
故应选C.
9.【答案】B
【解析】
【分析】
?本题考查的是垂径定理,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.根据题意知,已知弦长和弓形高,求半径直径,根据垂径定理和勾股定理求解即可.
【解答】
解:如图,设半径为r,过O作交AB于点D,连接OA、OB,则米,
设,则,
在中,
,即,
解得米,
故此输水管道的直径米.
故选B.
10.【答案】D
【解析】解:是弦CD的中点,
根据垂径定理:,
又则有:,
设OM是x米,
在中,有,
即:,
解得:,
所以.
故选D.
因为M是弦CD的中点,根据垂径定理,,则,在中,有,可求得OM,进而就可求得EM.
此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
11.【答案】10,6
【解析】
【分析】
本题结合勾股定理考查了垂径定理,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式成立,知道这三个量中的任意两个,就可以求出另外一个.
过点P的最长弦就是直径,最短弦就是垂直于OP的弦,根据垂径定理和勾股定理可求得.
【解答】
解:
过点P的最长弦就是直径,,
最短弦就是垂直于OP的弦,
如图所示,于P,
,,
,
弦.
故答案为:10,6.
12.【答案】6
【解析】
【分析】
本题利用了垂线段最短和垂径定理及勾股定理求解.根据垂线段最短,可以得到当时,点P到圆心O的距离最短.根据垂径定理和勾股定理即可求解.
【解答】
解:根据垂线段最短知,
当点P运动到时,点P到到点O的距离最短,
由垂径定理知,此时点P为AB中点,,
由勾股定理得,此时,
故答案为6.
13.【答案】49或7
【解析】
【分析】
本题考查了勾股定理和垂径定理,解答此题时要注意进行分类讨论,不要漏解.
由于弦AB、CD的具体位置不能确定,故应分两种情况进行讨论:弦AB和CD在圆心同侧;弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
【解答】
解:当弦AB和CD在圆心同侧时,如图,
过点O作,垂足为F,交AB于点E,连接OA,OC,
,
,
,,
,,
,
由勾股定理得:,,
则四边形ABDC的面积为:
当弦AB和CD在圆心异侧时,如图,
过点O作于点E,反向延长OE交CD于点F,连接OA,OC,
同理可得,,,
,
则四边形ABDC的面积为:
则四边形ABDC的面积为7或49.
故答案为49或7.
14.【答案】4
【解析】
【分析】
此题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧,勾股定理.由,则AB是过P的最短的弦,过P的最长的弦是圆的直径,首先根据垂径定理和勾股定理可以求出AB的长度,然后结合已知条件就可以求出弦长为整数的弦的条数.
【解答】
解:如图,
CD为过P点的直径,AB是与OP垂直的弦,连OA,
则过点P的所有的弦中CD最长,AB最短,并且,
,
,
在中
,,
,
,
过点P的弦中弦长可以为整数9,由圆的对称性得到弦长为9的弦有两条,
在过点P的所有的弦中,弦长为整数的弦的条数共有4条,
故答案为4.
15.【答案】26
【解析】
【分析】
本题主要考查了垂径定理和勾股定理,作出恰当的辅助线,利用定理是解答此题的关键.连接OA,根据垂径定理得,根据勾股定理即刻得到结论.
【解答】
解:连接OA,
,
,
在中,,
即,
,
水管横截面圆的半径是26cm,
故答案为26.
16.【答案】解:过A作于N,连接AB,
设的半径为R,则,
点B的坐标是,
,,
在中,由勾股定理得:,
即,
解得:,
,
点的坐标是,,
,AO过圆心A,
,
即,
,
点的坐标是.
【解析】本题考查了坐标与图形的性质,勾股定理,垂径定理等知识点,能求出半径AO的长是解此题的关键.根据勾股定理求出OA,求出BN,根据垂径定理求出,即可求出答案.
17.【答案】证明:过点O作,
,
,
又在中,
,
.
【解析】
【分析】本题考查的是垂径定理,根据题意作出辅助线,利用垂径定理求解是解答此题的关键.
过点O作,由等腰三角形的性质可知,再由垂径定理可知AE,故可得出结论.
18.【答案】解:如图,弦AB即为所求.
【解析】作直线OM,过点M作直线交于A,B,弦AB即为所求.
本题考查垂径定理,解题的关键是理解题意,灵活运用所学知识解决问题.
第2页,共2页
第1页,共1页
同课章节目录
