5.4 一元一次方程的应用(2) 课件(共27张PPT)
文档属性
| 名称 | 5.4 一元一次方程的应用(2) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:26:49 | ||
图片预览








文档简介
一元一次方程的应用2
列一元一次方程解决实际问题的一般步骤是:
知识回顾
解方程
检验
审题
设元
列方程
小学学过的公式.
长方形的周长:
C=2ab
长方体的体积:
V=abh
长方形的面积:
S=ab
正方体的体积:
V=a3
圆柱体的体积:
V=πr2h
你能运用上述的公式解决实际问题吗?
新课导入
例3 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框(如图中阴影部分).已知铺这个框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问标志性建筑的底面边长是多少米?
例题讲解
分析 阴影部分的面积= 144块边长为0.8米的正方形花岗石的面积.
阴影部分可以分割成4个长为(x+3.2)米,宽为3.2米的长方形.
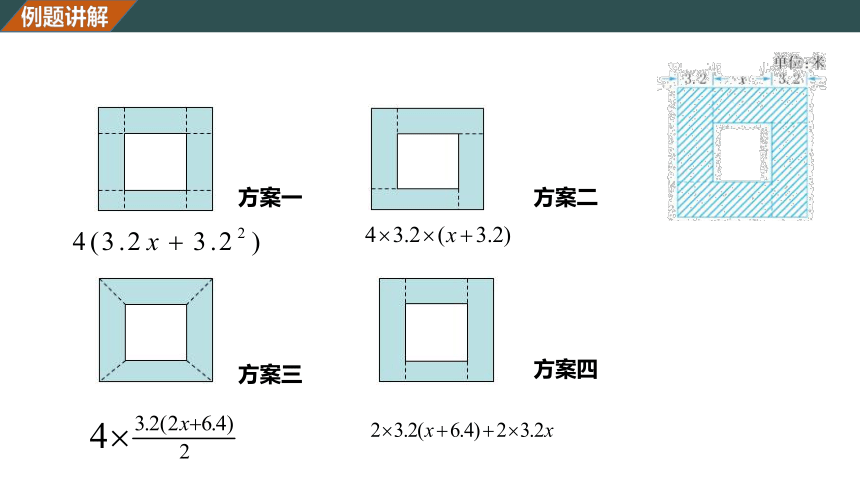
如图,若用x表示中间空白正方形的边长,怎样用含x的代数式表示阴影部分的面积呢?你能设计几种不同的计算方法?
例题讲解
方案一
方案二
方案三
方案四
例题讲解
解 :设标志性建筑底面的边长为x米,根据题意,得
4×3.2(x+3.2)=0.8×0.8×144,
解这个方程得 x=4,
答:这一标志性建筑底面边长为6米.
例题讲解
1.将一张正方形纸片剪去一个宽为 4 cm 的长条后,再从剩下的长方形纸片上剪去一个宽为 5 cm 的长条,如果两次剪下的长条面积正好相等,那么剪剩下的长方形纸片的面积为多少?
解 设正方形边长为x(cm),
由题意得:
得
所以,原正方形边长为 20 cm.
所以,剪剩下的长方形面积为(20-4)(20-5)=240 cm2 .
答:剪剩下的长方形纸片的面积为 240cm2 .
变式练习
1、在应用方程解决实际问题时,清楚地分辨各量之间的关系,尤其相等关系是建立方程的关键;
2、解题中的检验对确保答案的正确和合理很有帮助,解题时应养成良好的检验习惯,但具体过程可省略不写;
3、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变.
总结
你能测量出一个苹果的体积是多少吗?你怎么测量呢?
h
R
在测量过程中你发现了什么?
苹果的体积等于测量时上升部分的水的体积.
新课讲解
例4 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多长(不计损耗,结果 误差不超过1 mm)?
21cnjy.com
例题讲解
分析:1、在这个问题中的相等关系是:
锻造前的( )=锻造后的( );
2、如果设锻造前圆柱的高为x毫米,也既截取的圆柱长为x毫米,则圆柱的体积怎么表示 ?
3、锻造后长方体的长为( )毫米,宽为( )毫米,高为( )毫米,体积怎么计算?
4、如何列方程?
圆柱的体积
长方体的体积
V=π×1002×x
300
300
80
300×300×80
π×1002×x=300×300×80
例题分析
解:设截取圆柱的高为x mm,
根据题意,得
π×1002×x=300×300×80.
解这个方程,得
.
答:应截取钢柱的长约为230 mm.
例题讲解
例4 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多长(不计损耗,结果 误差不超过1 mm)?
Φ200
X
80
300
300
钢柱
长方体毛坯
有一个底面直径是20 cm,高12 cm的圆柱,工人师父要把它锻造成底面直径是10 cm的圆柱,工人师父想知道锻造后的圆柱有多高?你能告诉他吗?
本题中的相等关系是什么?
锻造前圆柱的体积=锻造后圆柱的体积.
根据这个等量关系怎样列方程?
解:设锻造后圆柱高为x厘米,根据题意,得π×102×12=π×52×x
解这个方程,得x=48
答:锻造后圆柱的高为48厘米.
21cnjy.com
变式练习
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
底面积、高度发生了变化,体积和质量都保持不变.
课内练习
围成的图形的面积发生了变化,但铁丝的长度不变.
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
课内练习
形状改变,体积不变.
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
课内练习
2.一书架能放厚为 6.3 cm 的书 45 本,现在准备放厚为 2.1 cm 的书,问能放这种书多少本?
答:能放这种 2.1 cm 厚的书135本.
解:设能放 2.1 cm 厚的书x本,
由题意可知:
课内练习
1.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )
A.18(42﹣x)=12x B.2×18(42﹣x)=12x
C.18(42﹣x)=2×12x D.18(21﹣x)=12x
课后练习
解:由题意可得,
12x×2=(42﹣x)×18,
故选C.
2.如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
【分析】设长方形的宽为x公分,抽出隔板后之水面高度为h公分,根据题意列出方程,求出方程的解即可.
课后练习
解:设长方形的宽为x公分,抽出隔板后之水面高度为h公分,长方形的长为130+70=200(公分)
????????????+????????????)????2×????????+????????????+????????)????2×????????=200?x?h,
?
解得:h=44,
故选B.
2.如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
课后练习
3.一个长方形的养鸡场的长边靠墙,墙长14米,其它三边用竹篱笆围成。现有长为35米的竹篱笆,小王打算用它围成一个鸡场,其中长比宽多5米;小赵也打算用它围成一个鸡场,其中长比宽多2米。你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?
课后练习
[分析]
是否符合实际关键看和墙相对的一边是不是超过14米,若超过14米,就是不合实际;所以我们就需要根据小王和小赵的设计求出这一边的长度并和14米比较,而此时就需找到“等量关系”建立方程。
14米
?
课后练习
解:先看小王的设计:
设宽为x米,则长为 (x+5) 米,根据题意,得
2x+(x+5)=35
解得 x= 10
因为小王设计的长为X+5=10+5=15米> 14米, 所以小王的设计不符合实际。
再看小赵的设计:
设设计宽为x米,则长为(x+2) 米 ,根据题意,得
2x+(x+2)=35
解得 x=11
因为小赵的设计的长为 x + 2 = 1 1+ 2=13米< 14米,
所以小赵的设计符合要求。
此时,鸡场的面积为 11×13=143平方米。
14米
课后练习
1、在解决图形问题时,要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
21cnjy.com
课后总结
课后作业
教材练习题
谢
谢
观
看
列一元一次方程解决实际问题的一般步骤是:
知识回顾
解方程
检验
审题
设元
列方程
小学学过的公式.
长方形的周长:
C=2ab
长方体的体积:
V=abh
长方形的面积:
S=ab
正方体的体积:
V=a3
圆柱体的体积:
V=πr2h
你能运用上述的公式解决实际问题吗?
新课导入
例3 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框(如图中阴影部分).已知铺这个框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问标志性建筑的底面边长是多少米?
例题讲解
分析 阴影部分的面积= 144块边长为0.8米的正方形花岗石的面积.
阴影部分可以分割成4个长为(x+3.2)米,宽为3.2米的长方形.
如图,若用x表示中间空白正方形的边长,怎样用含x的代数式表示阴影部分的面积呢?你能设计几种不同的计算方法?
例题讲解
方案一
方案二
方案三
方案四
例题讲解
解 :设标志性建筑底面的边长为x米,根据题意,得
4×3.2(x+3.2)=0.8×0.8×144,
解这个方程得 x=4,
答:这一标志性建筑底面边长为6米.
例题讲解
1.将一张正方形纸片剪去一个宽为 4 cm 的长条后,再从剩下的长方形纸片上剪去一个宽为 5 cm 的长条,如果两次剪下的长条面积正好相等,那么剪剩下的长方形纸片的面积为多少?
解 设正方形边长为x(cm),
由题意得:
得
所以,原正方形边长为 20 cm.
所以,剪剩下的长方形面积为(20-4)(20-5)=240 cm2 .
答:剪剩下的长方形纸片的面积为 240cm2 .
变式练习
1、在应用方程解决实际问题时,清楚地分辨各量之间的关系,尤其相等关系是建立方程的关键;
2、解题中的检验对确保答案的正确和合理很有帮助,解题时应养成良好的检验习惯,但具体过程可省略不写;
3、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变.
总结
你能测量出一个苹果的体积是多少吗?你怎么测量呢?
h
R
在测量过程中你发现了什么?
苹果的体积等于测量时上升部分的水的体积.
新课讲解
例4 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多长(不计损耗,结果 误差不超过1 mm)?
21cnjy.com
例题讲解
分析:1、在这个问题中的相等关系是:
锻造前的( )=锻造后的( );
2、如果设锻造前圆柱的高为x毫米,也既截取的圆柱长为x毫米,则圆柱的体积怎么表示 ?
3、锻造后长方体的长为( )毫米,宽为( )毫米,高为( )毫米,体积怎么计算?
4、如何列方程?
圆柱的体积
长方体的体积
V=π×1002×x
300
300
80
300×300×80
π×1002×x=300×300×80
例题分析
解:设截取圆柱的高为x mm,
根据题意,得
π×1002×x=300×300×80.
解这个方程,得
.
答:应截取钢柱的长约为230 mm.
例题讲解
例4 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多长(不计损耗,结果 误差不超过1 mm)?
Φ200
X
80
300
300
钢柱
长方体毛坯
有一个底面直径是20 cm,高12 cm的圆柱,工人师父要把它锻造成底面直径是10 cm的圆柱,工人师父想知道锻造后的圆柱有多高?你能告诉他吗?
本题中的相等关系是什么?
锻造前圆柱的体积=锻造后圆柱的体积.
根据这个等量关系怎样列方程?
解:设锻造后圆柱高为x厘米,根据题意,得π×102×12=π×52×x
解这个方程,得x=48
答:锻造后圆柱的高为48厘米.
21cnjy.com
变式练习
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
底面积、高度发生了变化,体积和质量都保持不变.
课内练习
围成的图形的面积发生了变化,但铁丝的长度不变.
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
课内练习
形状改变,体积不变.
1.请指出下列过程中,哪些量发生了变化,哪些量保持不变.
⑴把一小杯水倒入另一只大杯中.
⑵用一根15 cm长的铁丝围成一个三角形,然后把它改围成长方形.
⑶用一块橡皮泥先做成一个立方体,再把它改做成球.
课内练习
2.一书架能放厚为 6.3 cm 的书 45 本,现在准备放厚为 2.1 cm 的书,问能放这种书多少本?
答:能放这种 2.1 cm 厚的书135本.
解:设能放 2.1 cm 厚的书x本,
由题意可知:
课内练习
1.某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )
A.18(42﹣x)=12x B.2×18(42﹣x)=12x
C.18(42﹣x)=2×12x D.18(21﹣x)=12x
课后练习
解:由题意可得,
12x×2=(42﹣x)×18,
故选C.
2.如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
【分析】设长方形的宽为x公分,抽出隔板后之水面高度为h公分,根据题意列出方程,求出方程的解即可.
课后练习
解:设长方形的宽为x公分,抽出隔板后之水面高度为h公分,长方形的长为130+70=200(公分)
????????????+????????????)????2×????????+????????????+????????)????2×????????=200?x?h,
?
解得:h=44,
故选B.
2.如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
课后练习
3.一个长方形的养鸡场的长边靠墙,墙长14米,其它三边用竹篱笆围成。现有长为35米的竹篱笆,小王打算用它围成一个鸡场,其中长比宽多5米;小赵也打算用它围成一个鸡场,其中长比宽多2米。你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?
课后练习
[分析]
是否符合实际关键看和墙相对的一边是不是超过14米,若超过14米,就是不合实际;所以我们就需要根据小王和小赵的设计求出这一边的长度并和14米比较,而此时就需找到“等量关系”建立方程。
14米
?
课后练习
解:先看小王的设计:
设宽为x米,则长为 (x+5) 米,根据题意,得
2x+(x+5)=35
解得 x= 10
因为小王设计的长为X+5=10+5=15米> 14米, 所以小王的设计不符合实际。
再看小赵的设计:
设设计宽为x米,则长为(x+2) 米 ,根据题意,得
2x+(x+2)=35
解得 x=11
因为小赵的设计的长为 x + 2 = 1 1+ 2=13米< 14米,
所以小赵的设计符合要求。
此时,鸡场的面积为 11×13=143平方米。
14米
课后练习
1、在解决图形问题时,要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
21cnjy.com
课后总结
课后作业
教材练习题
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
