5.4一元一次方程的应用(3) 课件(共30张PPT)
文档属性
| 名称 | 5.4一元一次方程的应用(3) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:29:03 | ||
图片预览








文档简介
一元一次方程的应用3
1、在解决图形问题时,要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
21cnjy.com
知识回顾
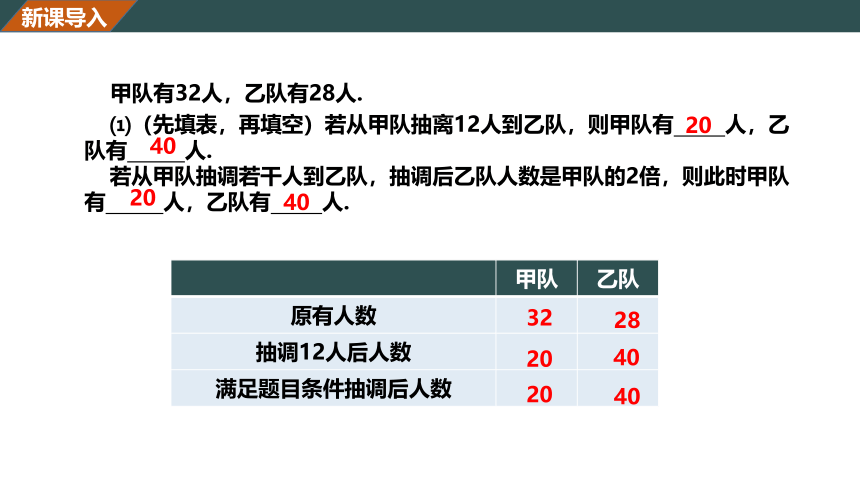
甲队有32人,乙队有28人.
⑴(先填表,再填空)若从甲队抽离12人到乙队,则甲队有 人,乙队有 人.
若从甲队抽调若干人到乙队,抽调后乙队人数是甲队的2倍,则此时甲队有 人,乙队有 人.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲队
乙队
原有人数
抽调12人后人数
满足题目条件抽调后人数
20
40
20
40
40
40
20
20
32
28
新课导入
新课导入
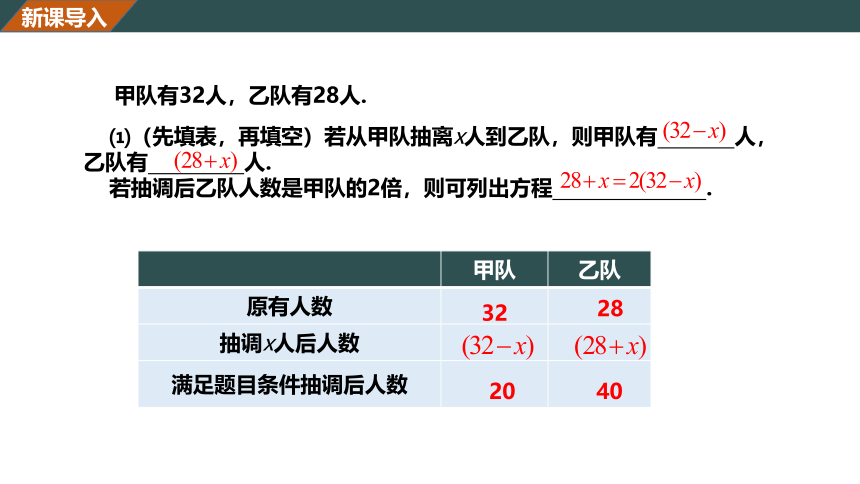
甲队有32人,乙队有28人.
⑴(先填表,再填空)若从甲队抽离x人到乙队,则甲队有 人,乙队有 人.
若抽调后乙队人数是甲队的2倍,则可列出方程 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲队
乙队
原有人数
抽调x人后人数
满足题目条件抽调后人数
40
20
32
28
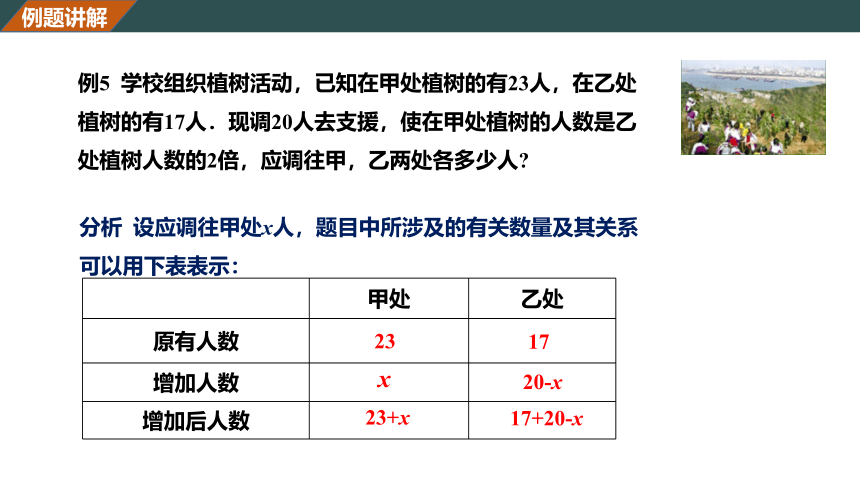
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲,乙两处各多少人?
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
{5940675A-B579-460E-94D1-54222C63F5DA}
甲处
乙处
原有人数
增加人数
增加后人数
23
17
x
20-x
23+x
17+20-x
例题讲解
甲处增加后人数=2×乙处增加后人数.
本题的相等关系是什么?
解:设应调往甲处x人,根据题意,得
23+x=2(17+20-x)
解这个方程,得x=17
∴20-x=3
答:应调往甲处17人,乙处3人.
例题讲解
总结
在解决调配问题时,我们一般可以通过列表法分析数量关系,再用一元一次方程解题.
某制衣厂现有24名制作服装工人,每天都制作某种品牌衬衫和裤子,每人每天可制作衬衫3件或裤子5条,若该厂要求每天制作的衬衫和裤子数量相等,则应安排制作衬衫和裤子各多少人?
解:设应安排制作衬衫x人,
根据题意得
解得
答:应安排制作衬衫15人,制作裤子9人.
变式练习
1、甲每天生产某种零件80个,3天能生产________个零件.
2、乙每天生产某种零件x个,5天能生产______个零件.
3、甲每天生产某种零件80个,乙每天生产某种零件x个.他们5天一共生产_____________个零件.
4、甲每天生产某种零件80个,乙每天生产这种零件x个.甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产 _______________个零件.
3×80
5x
5(80+x)
3×80+5×80+5x
工程问题的基本数量关系是什么?
工作总量=工作时间×工作效率.
例题讲解
例6 甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个.问乙每天生产这种零件多少个?
分析 用示意图来分析本题中的数量关系如下:
前3天甲生产零件的个数
后5天生产零件的个数
甲生产零件的个数
乙生产零件的个数
940个
本题的相等关系是什么?
例题讲解
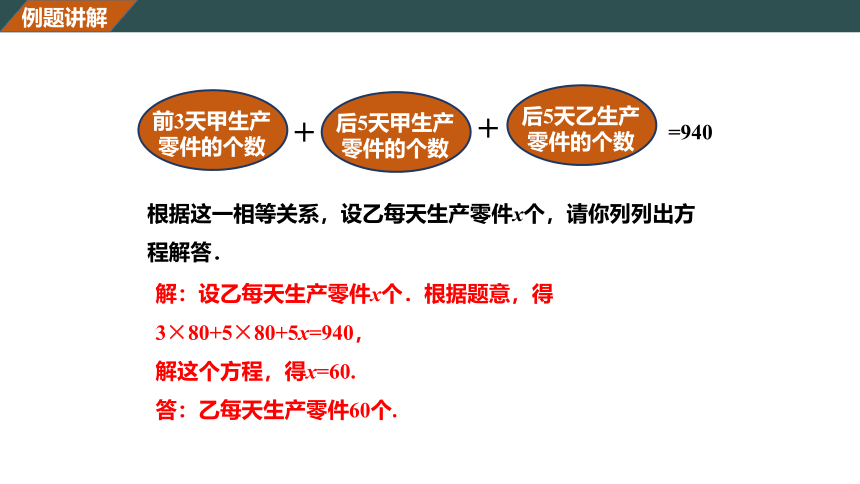
前3天甲生产零件的个数
+
后5天甲生产零件的个数
+
后5天乙生产零件的个数
=940
根据这一相等关系,设乙每天生产零件x个,请你列列出方程解答.
解:设乙每天生产零件x个.根据题意,得
3×80+5×80+5x=940,
解这个方程,得x=60.
答:乙每天生产零件60个.
例题讲解
一件工作,甲单独完成需要50天,乙单独完成需要40天.甲、乙合作20天后,剩下的工作由甲单独完成,那么甲还需要多少天才能完成这件工作?
分析 用示意图分析数量关系如下图所示:
20天后甲的工作量
20天乙完成的工作量
甲的工作量
20天甲完成的工作量
工作总量1
变式练习
本题的相等关系是什么?
20天乙完成的工作量+20天甲完成的工作量+20天后甲的工作量=1.
解:设甲还需要x天才能完成这件工作,根据题意,得
,
解得,x=5,
答:甲还需要5天才能完成这件工作.
变式练习
在解决工程问题时,我们一般可以通过画线段图,分析数量关系,再用一元一次方程解题.
总结
某种商品的进价是每件 400 元,原标价为每件 600 元,商店打折销售该商品时的毛利率为 5%,问该商品是打几折销售的( )?
毛利率=
销售价-进价
进价
解:设该商品销售的折扣率为x ,
由题意得
答:该商品是打七折销售的.
课内练习
某商店有两种不同型号的计算器的出售价都是64元,卖出其中一种计算器商店盈利为进货价的60%,卖出另一种商店亏损进货价的20%.若卖出这两种计算器1台,这家商店的盈亏情况如何?
解:设一个价钱为x元,另一个价钱为y元,依题意得:
x(1+60%)=64,
y(1-20%)=64,
所以:x=40,y=80,
则64×2-(40+80)=128-120=8.
故盈利8元.
课内练习
1.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )
A.518=2(106+x) B.518-x=2×106 21·cn·jy·com
C.518-x=2(106+x) D.518+x=2(106-x)
【解析】设从甲煤场运煤x吨到乙煤场,
可得:518-x=2(106+x),故选C.
课后练习
2.超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x-10=90 B.0.08x-10=90
C.90-0.8x=10 D.x-0.8x-10=90
【解析】设某种书包原价每个x元,可得:0.8x-10=90,故选A.
课后练习
10
60
0.75x
1. 一件商品的销售价为100元,进价为90元,则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,售价是 。
3.一件夹克成本价为50元,提价50%后标价,再按标价的8折出售,则售价为 元。
三、填空
课后练习
4.某厂一车间有64人,二车间有56人.现因工作需要,要求第一车间人数是第二车间人数的一半.问需从第一车间调多少人到第二车间?
【分析】设需从第一车间调x人到第二车间,第一车间人数是(64﹣x)人,第二车间人数是56+x人,根据第一车间人数是第二车间人数的一半,列出方程即可.
课后练习
4.某厂一车间有64人,二车间有56人.现因工作需要,要求第一车间人数是第二车间人数的一半.问需从第一车间调多少人到第二车间?
解:设需从第一车间调x人到第二车间,根据题意得:
2(64﹣x)=56+x,
解得x=24;
答:需从第一车间调24人到第二车间.
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲仓库
乙仓库
A工地
x
B工地
x+10
课后练习
解:(1)设甲仓库运到A工地水泥的吨数为x吨,则运到B地水泥的吨数为(100﹣x)吨,
乙仓库运到A工地水泥的吨数为(70﹣x)吨,则运到B地水泥的吨数为(x+10)吨,
补全表格如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲仓库
乙仓库
A工地
x
70﹣x
B工地
100﹣x
x+10
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(2)用含x的代数式表示运送甲仓库100吨水泥的运费为 元.(写出化简后的结果)
课后练习
(2)运送甲仓库100吨水泥的运费为140x+150(100﹣x)=﹣10x+15000,
故答案为:﹣10x+15000;
?
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
课后练习
?(3)140x+150(100﹣x)+200(70﹣x)+80(x+10)=25900,
整理得:﹣130x+3900=0.
课后练习
1、调配问题往往要借助列表法或图示法理清问题中的等量关系.
2、解工程问题时,常把工作量看成“1”.一般可以通过画线段图,分析数量关系,再用一元一次方程解题.
3、解决利润问题时要把握进价、售价、利润和利润率之间的关系.
课后总结
课后作业
教材练习题
谢
谢
观
看
1、在解决图形问题时,要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
21cnjy.com
知识回顾
甲队有32人,乙队有28人.
⑴(先填表,再填空)若从甲队抽离12人到乙队,则甲队有 人,乙队有 人.
若从甲队抽调若干人到乙队,抽调后乙队人数是甲队的2倍,则此时甲队有 人,乙队有 人.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲队
乙队
原有人数
抽调12人后人数
满足题目条件抽调后人数
20
40
20
40
40
40
20
20
32
28
新课导入
新课导入
甲队有32人,乙队有28人.
⑴(先填表,再填空)若从甲队抽离x人到乙队,则甲队有 人,乙队有 人.
若抽调后乙队人数是甲队的2倍,则可列出方程 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲队
乙队
原有人数
抽调x人后人数
满足题目条件抽调后人数
40
20
32
28
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲,乙两处各多少人?
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
{5940675A-B579-460E-94D1-54222C63F5DA}
甲处
乙处
原有人数
增加人数
增加后人数
23
17
x
20-x
23+x
17+20-x
例题讲解
甲处增加后人数=2×乙处增加后人数.
本题的相等关系是什么?
解:设应调往甲处x人,根据题意,得
23+x=2(17+20-x)
解这个方程,得x=17
∴20-x=3
答:应调往甲处17人,乙处3人.
例题讲解
总结
在解决调配问题时,我们一般可以通过列表法分析数量关系,再用一元一次方程解题.
某制衣厂现有24名制作服装工人,每天都制作某种品牌衬衫和裤子,每人每天可制作衬衫3件或裤子5条,若该厂要求每天制作的衬衫和裤子数量相等,则应安排制作衬衫和裤子各多少人?
解:设应安排制作衬衫x人,
根据题意得
解得
答:应安排制作衬衫15人,制作裤子9人.
变式练习
1、甲每天生产某种零件80个,3天能生产________个零件.
2、乙每天生产某种零件x个,5天能生产______个零件.
3、甲每天生产某种零件80个,乙每天生产某种零件x个.他们5天一共生产_____________个零件.
4、甲每天生产某种零件80个,乙每天生产这种零件x个.甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产 _______________个零件.
3×80
5x
5(80+x)
3×80+5×80+5x
工程问题的基本数量关系是什么?
工作总量=工作时间×工作效率.
例题讲解
例6 甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个.问乙每天生产这种零件多少个?
分析 用示意图来分析本题中的数量关系如下:
前3天甲生产零件的个数
后5天生产零件的个数
甲生产零件的个数
乙生产零件的个数
940个
本题的相等关系是什么?
例题讲解
前3天甲生产零件的个数
+
后5天甲生产零件的个数
+
后5天乙生产零件的个数
=940
根据这一相等关系,设乙每天生产零件x个,请你列列出方程解答.
解:设乙每天生产零件x个.根据题意,得
3×80+5×80+5x=940,
解这个方程,得x=60.
答:乙每天生产零件60个.
例题讲解
一件工作,甲单独完成需要50天,乙单独完成需要40天.甲、乙合作20天后,剩下的工作由甲单独完成,那么甲还需要多少天才能完成这件工作?
分析 用示意图分析数量关系如下图所示:
20天后甲的工作量
20天乙完成的工作量
甲的工作量
20天甲完成的工作量
工作总量1
变式练习
本题的相等关系是什么?
20天乙完成的工作量+20天甲完成的工作量+20天后甲的工作量=1.
解:设甲还需要x天才能完成这件工作,根据题意,得
,
解得,x=5,
答:甲还需要5天才能完成这件工作.
变式练习
在解决工程问题时,我们一般可以通过画线段图,分析数量关系,再用一元一次方程解题.
总结
某种商品的进价是每件 400 元,原标价为每件 600 元,商店打折销售该商品时的毛利率为 5%,问该商品是打几折销售的( )?
毛利率=
销售价-进价
进价
解:设该商品销售的折扣率为x ,
由题意得
答:该商品是打七折销售的.
课内练习
某商店有两种不同型号的计算器的出售价都是64元,卖出其中一种计算器商店盈利为进货价的60%,卖出另一种商店亏损进货价的20%.若卖出这两种计算器1台,这家商店的盈亏情况如何?
解:设一个价钱为x元,另一个价钱为y元,依题意得:
x(1+60%)=64,
y(1-20%)=64,
所以:x=40,y=80,
则64×2-(40+80)=128-120=8.
故盈利8元.
课内练习
1.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )
A.518=2(106+x) B.518-x=2×106 21·cn·jy·com
C.518-x=2(106+x) D.518+x=2(106-x)
【解析】设从甲煤场运煤x吨到乙煤场,
可得:518-x=2(106+x),故选C.
课后练习
2.超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x-10=90 B.0.08x-10=90
C.90-0.8x=10 D.x-0.8x-10=90
【解析】设某种书包原价每个x元,可得:0.8x-10=90,故选A.
课后练习
10
60
0.75x
1. 一件商品的销售价为100元,进价为90元,则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,售价是 。
3.一件夹克成本价为50元,提价50%后标价,再按标价的8折出售,则售价为 元。
三、填空
课后练习
4.某厂一车间有64人,二车间有56人.现因工作需要,要求第一车间人数是第二车间人数的一半.问需从第一车间调多少人到第二车间?
【分析】设需从第一车间调x人到第二车间,第一车间人数是(64﹣x)人,第二车间人数是56+x人,根据第一车间人数是第二车间人数的一半,列出方程即可.
课后练习
4.某厂一车间有64人,二车间有56人.现因工作需要,要求第一车间人数是第二车间人数的一半.问需从第一车间调多少人到第二车间?
解:设需从第一车间调x人到第二车间,根据题意得:
2(64﹣x)=56+x,
解得x=24;
答:需从第一车间调24人到第二车间.
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲仓库
乙仓库
A工地
x
B工地
x+10
课后练习
解:(1)设甲仓库运到A工地水泥的吨数为x吨,则运到B地水泥的吨数为(100﹣x)吨,
乙仓库运到A工地水泥的吨数为(70﹣x)吨,则运到B地水泥的吨数为(x+10)吨,
补全表格如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
甲仓库
乙仓库
A工地
x
70﹣x
B工地
100﹣x
x+10
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(2)用含x的代数式表示运送甲仓库100吨水泥的运费为 元.(写出化简后的结果)
课后练习
(2)运送甲仓库100吨水泥的运费为140x+150(100﹣x)=﹣10x+15000,
故答案为:﹣10x+15000;
?
课后练习
5.甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
课后练习
?(3)140x+150(100﹣x)+200(70﹣x)+80(x+10)=25900,
整理得:﹣130x+3900=0.
课后练习
1、调配问题往往要借助列表法或图示法理清问题中的等量关系.
2、解工程问题时,常把工作量看成“1”.一般可以通过画线段图,分析数量关系,再用一元一次方程解题.
3、解决利润问题时要把握进价、售价、利润和利润率之间的关系.
课后总结
课后作业
教材练习题
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
