5.2 等式的基本性质 课件(共27张PPT)
文档属性
| 名称 | 5.2 等式的基本性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览







文档简介
等式的基本性质
1、方程的两边都是整式,只含有一个未知数,并且未知数的指数是一次,这样的方程叫做一元一次方程.
2、使方程左右两边的值相等的未知数的值叫做方程的解.
3、根据数量关系或简单问题情境列一元一次方程.
21cnjy.com
知识回顾
4、什么叫做等式?
用等号“=”来表示相等关系的式子,叫做等式.
比较下图中左、右两个天平图,你有什么发现?
一架平衡的天平两边同时加上(或减去)相同质量的砝码,天平仍保持平衡.
新课导入
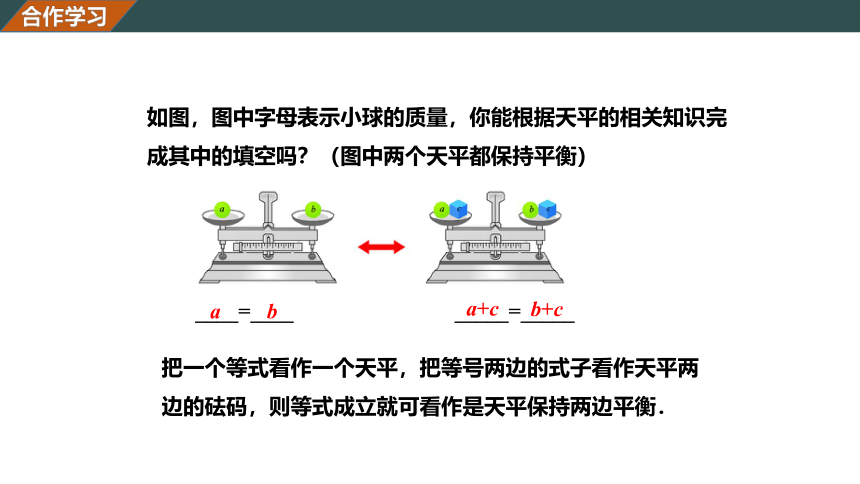
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
合作学习
____=____ _____=_____
a
b
a+c
b+c
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你发现了等式的哪些性质?
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立.
等式的性质1 等式的两边都 加上(或减去)同一个数或式,所得结果仍是等式.
用字母可表示为:
如果a=b,那么a±c=b±c.
小结
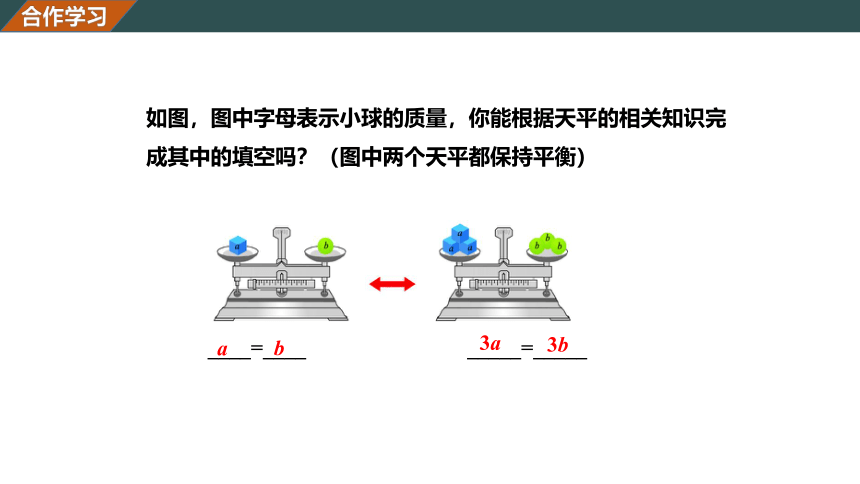
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
合作学习
____=____ _____=_____
a
b
3a
3b
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你又能发现等式的哪些性质?
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
用字母可表示为:
如果a=b,那么ac=bc,或 .
小结
已知x+3=1,下列等式成立吗?根据是什么?
(1)3=1-x; (2)-2(x+3)=-2;
(3) ; (4)x=1-3.
解:(1)成立,根据等式的性质1,两边都减去x;
(2)成立,根据等式的性质2,两边都乘以-2;
(3)成立,根据等式的性质2,两边都除以3;
(4)成立,根据等式的性质1,两边都减去3.
做一做
例1 已知2x-5y=0,且y≠0.判断下列等式是否成立,并说明理由.
(1)2x=5y; (2) .
解:(1)成立.理由如下:已知2x-5y=0,
两边都加上5y,得 2x-5y+5y=0+5y(等式的性质1),
∴2x=5y.
(2)成立.理由如下:由(1)知2x=5y,而y≠0,
两边都除以2y,得 (等式的性质2).
例题讲解
方程是含有未知数的等式,方程中的未知数与已知数一起参与了运算.通过运算将一元一次方程一步一步变形,最后变形成“x=a(a为已知数)”的形式,就求出了未知数的值,即方程的解.等式的性质是方程变形的依据.
小结
【点拨】本题易误以为C项没有应用等式的性质,而是左边平方,右边乘x,其实是两边同时乘x,因而C项是正确的;A项在同时乘m的基础上再同时减6,A正确;B项同时除以t2+1(t2+1≠0),故正确.D项同时除以x,其中x可能为0,故D错误.
【答案】 D
变式训练
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
小结
例2 利用等式的性质解下列方程:
(1)5x=50+4x; (2)8-2x=9-4x.
解:(1)方程的两边都减去4x,得
5x-4x=50+4x-4x(等式的性质1).
合并同类项,得 x=50.
检验:把x=50代入方程,
左边=5×50=250,右边=50+4×50=250,
∵左边=右边,
∴ x=50是方程的解.
例题讲解
(2)方程的两边都加上4x,得 8-2x+4x=9-4x+4x.
合并同类项,得 8+2x=9 .
两边都减去8,得 2x=1 .
两边都除以2,得 .
依据什么?
(等式的性质2)
例2 利用等式的性质解下列方程:
(1)5x=50+4x; (2)8-2x=9-4x.
例题讲解
利用等式的性质解下列方程.
(1)x-4=7;
变式训练
B
课后练习
D
课后练习
3.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2 020个白色菱形纸片,则n的值为________.
673
课后练习
【点拨】认真观察图案,确定图案变化规律:第1个图案中有4个白色菱形纸片,第2个图案中有7个白色菱形纸片,…,每个图案都比前一个图案多3个白色菱形纸片,所以第n(n是正整数)个图案中白色菱形纸片的个数为3n+1,令3n+1=2 020,得n=673.
课后练习
课后练习
4.已知 ,求:
⑴说明2a=-3b成立的理由;
⑵ a与b的比为多少?
⑴等式两边都乘以6,得2a+3b=0(等式的性质2).
等式两边都减去3b,得2a=-3b.
⑵在等式2a=-3b的两边同除以2b,得
5.将等式 2a=2b 的两边都减去 a+b,可得a-b=b-a,再两边都除以(a-b),得 1=-1.这个结果显然是错误的!你知道错在哪里吗?
解
因为除数不能为0,
所以等式两边不能都除以a-b.
课后练习
6.利用等式的性质解方程:
(1)5+x=﹣2
(2)3x+6=31﹣2x.
(1)5+x=﹣2
5+x﹣5=﹣2﹣5
x=﹣7;
?
课后练习
(2)3x+6=31﹣2x
3x+6+2x﹣6=31﹣2x+2x﹣6
5x=25
x=5.
7.观察下列变形:
∵x=1,①
∴3x﹣2x=3﹣2,②
∴3x﹣3=2x﹣2,③
∴3(x﹣1)=2(x﹣1),④
∴3=2.⑤
(1)由②到③这一步是怎样变形的?
(2)发生错误的变形是哪一步?其原因是什么?
【分析】(1)根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立,可得答案;
(2)根据等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
课后练习
解:(1)②到③这一步是两边都加(2x﹣3);
(2)第⑤错误,原因是两边都除以0.
8.小明学习了等式的性质后对小亮说:“我发现4可以等于3,你看,这里有一个方程4x-2=3x-2,两边同时加2,得4x=3x,两边同时除以x,得4=3.”
(1)请你想一想,小明的说法对吗?为什么?
解:不对.因为忽略了x的值为0时,不能在等式4x=3x的两边同时除以x.
课后练习
(2)你能用等式的性质求出方程4x-2=3x-2的解吗?
解:方程的两边同时加2,得4x=3x,方程的两边同时减3x,得x=0.
1. 等式的性质:
等式的性质1 等式的两边都 加上(或减去)同一个数或式,所得结果仍是等式.
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
课后总结
课后作业
教材练习题
谢
谢
观
看
1、方程的两边都是整式,只含有一个未知数,并且未知数的指数是一次,这样的方程叫做一元一次方程.
2、使方程左右两边的值相等的未知数的值叫做方程的解.
3、根据数量关系或简单问题情境列一元一次方程.
21cnjy.com
知识回顾
4、什么叫做等式?
用等号“=”来表示相等关系的式子,叫做等式.
比较下图中左、右两个天平图,你有什么发现?
一架平衡的天平两边同时加上(或减去)相同质量的砝码,天平仍保持平衡.
新课导入
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
合作学习
____=____ _____=_____
a
b
a+c
b+c
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你发现了等式的哪些性质?
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立.
等式的性质1 等式的两边都 加上(或减去)同一个数或式,所得结果仍是等式.
用字母可表示为:
如果a=b,那么a±c=b±c.
小结
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
合作学习
____=____ _____=_____
a
b
3a
3b
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你又能发现等式的哪些性质?
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
用字母可表示为:
如果a=b,那么ac=bc,或 .
小结
已知x+3=1,下列等式成立吗?根据是什么?
(1)3=1-x; (2)-2(x+3)=-2;
(3) ; (4)x=1-3.
解:(1)成立,根据等式的性质1,两边都减去x;
(2)成立,根据等式的性质2,两边都乘以-2;
(3)成立,根据等式的性质2,两边都除以3;
(4)成立,根据等式的性质1,两边都减去3.
做一做
例1 已知2x-5y=0,且y≠0.判断下列等式是否成立,并说明理由.
(1)2x=5y; (2) .
解:(1)成立.理由如下:已知2x-5y=0,
两边都加上5y,得 2x-5y+5y=0+5y(等式的性质1),
∴2x=5y.
(2)成立.理由如下:由(1)知2x=5y,而y≠0,
两边都除以2y,得 (等式的性质2).
例题讲解
方程是含有未知数的等式,方程中的未知数与已知数一起参与了运算.通过运算将一元一次方程一步一步变形,最后变形成“x=a(a为已知数)”的形式,就求出了未知数的值,即方程的解.等式的性质是方程变形的依据.
小结
【点拨】本题易误以为C项没有应用等式的性质,而是左边平方,右边乘x,其实是两边同时乘x,因而C项是正确的;A项在同时乘m的基础上再同时减6,A正确;B项同时除以t2+1(t2+1≠0),故正确.D项同时除以x,其中x可能为0,故D错误.
【答案】 D
变式训练
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
小结
例2 利用等式的性质解下列方程:
(1)5x=50+4x; (2)8-2x=9-4x.
解:(1)方程的两边都减去4x,得
5x-4x=50+4x-4x(等式的性质1).
合并同类项,得 x=50.
检验:把x=50代入方程,
左边=5×50=250,右边=50+4×50=250,
∵左边=右边,
∴ x=50是方程的解.
例题讲解
(2)方程的两边都加上4x,得 8-2x+4x=9-4x+4x.
合并同类项,得 8+2x=9 .
两边都减去8,得 2x=1 .
两边都除以2,得 .
依据什么?
(等式的性质2)
例2 利用等式的性质解下列方程:
(1)5x=50+4x; (2)8-2x=9-4x.
例题讲解
利用等式的性质解下列方程.
(1)x-4=7;
变式训练
B
课后练习
D
课后练习
3.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2 020个白色菱形纸片,则n的值为________.
673
课后练习
【点拨】认真观察图案,确定图案变化规律:第1个图案中有4个白色菱形纸片,第2个图案中有7个白色菱形纸片,…,每个图案都比前一个图案多3个白色菱形纸片,所以第n(n是正整数)个图案中白色菱形纸片的个数为3n+1,令3n+1=2 020,得n=673.
课后练习
课后练习
4.已知 ,求:
⑴说明2a=-3b成立的理由;
⑵ a与b的比为多少?
⑴等式两边都乘以6,得2a+3b=0(等式的性质2).
等式两边都减去3b,得2a=-3b.
⑵在等式2a=-3b的两边同除以2b,得
5.将等式 2a=2b 的两边都减去 a+b,可得a-b=b-a,再两边都除以(a-b),得 1=-1.这个结果显然是错误的!你知道错在哪里吗?
解
因为除数不能为0,
所以等式两边不能都除以a-b.
课后练习
6.利用等式的性质解方程:
(1)5+x=﹣2
(2)3x+6=31﹣2x.
(1)5+x=﹣2
5+x﹣5=﹣2﹣5
x=﹣7;
?
课后练习
(2)3x+6=31﹣2x
3x+6+2x﹣6=31﹣2x+2x﹣6
5x=25
x=5.
7.观察下列变形:
∵x=1,①
∴3x﹣2x=3﹣2,②
∴3x﹣3=2x﹣2,③
∴3(x﹣1)=2(x﹣1),④
∴3=2.⑤
(1)由②到③这一步是怎样变形的?
(2)发生错误的变形是哪一步?其原因是什么?
【分析】(1)根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立,可得答案;
(2)根据等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
课后练习
解:(1)②到③这一步是两边都加(2x﹣3);
(2)第⑤错误,原因是两边都除以0.
8.小明学习了等式的性质后对小亮说:“我发现4可以等于3,你看,这里有一个方程4x-2=3x-2,两边同时加2,得4x=3x,两边同时除以x,得4=3.”
(1)请你想一想,小明的说法对吗?为什么?
解:不对.因为忽略了x的值为0时,不能在等式4x=3x的两边同时除以x.
课后练习
(2)你能用等式的性质求出方程4x-2=3x-2的解吗?
解:方程的两边同时加2,得4x=3x,方程的两边同时减3x,得x=0.
1. 等式的性质:
等式的性质1 等式的两边都 加上(或减去)同一个数或式,所得结果仍是等式.
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
课后总结
课后作业
教材练习题
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
