6.4 线段的和差 课件(共23张PPT)
文档属性
| 名称 | 6.4 线段的和差 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:43:32 | ||
图片预览








文档简介
第6章 图形的初步知识
6.4??线段的和差
1、比较线段长短的方法:度量法和叠合法
2、用尺规作线段等于已知线段
3、基本实事:两点之间线段最短
4、两点之间的距离是连接两点的线段的长度
知识回顾
教学目标:
1.理解线段的和差的意义.
2.会用直尺和圆规作两条线段的和与差.
3.理解线段的中点的概念,会用刻度尺二等分一条线段.
4.会进行有关线段的和、差、倍、分的简单计算.
重难点:
●本节教学的重点是线段的和差的概念,这是相关作图和计算的依据.
●例2涉及较多的线段和较复杂的数量关系,是本节教学中的难点.
目标难点
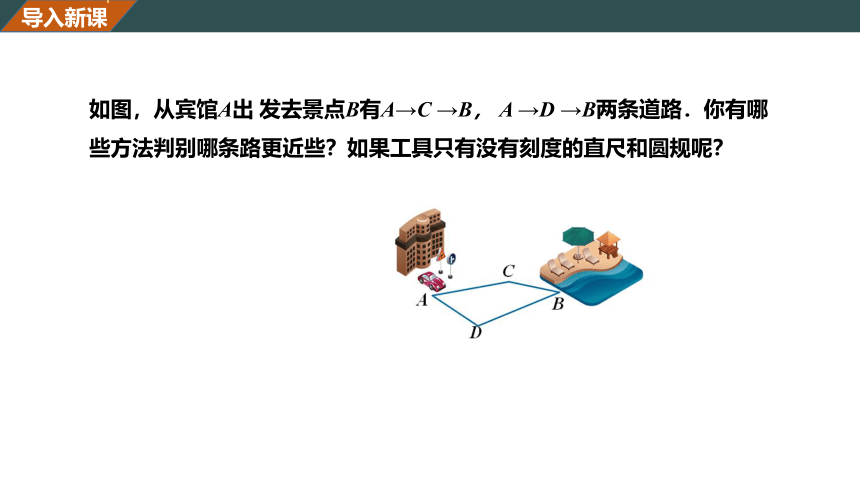
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
导入新课
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
新课讲解
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
归纳
如图,C是线段AB上的一点,请完成下面的填空.
(1)AC+CB=___________;
(2)AB-CB=___________;
(3)BC=__________-AC.
AB
AC
AB
做一做
A
C
B
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
21世纪教育网
例题讲解
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
例题讲解
如图,已知线段a,b,c,用直尺和圆规画线段,使得:
(1)AB=a-b;(2)OF=a-2b+c.
【解】 (1)画法:①画射线AM;
②在射线AM上截取AB=a,在线段AB的反方向截取BC=b;
线段AC就是所求的线段a-b.如解图①.
(2)画法:①画射线ON;
②在射线ON上依次截取OD=a,DE=c;
③在线段OE的反方向截取EF=2b.
线段OF就是所求的线段a-2b+c.如解图②.
变式训练
拿出一张白纸,对折这张白纸.把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
点C具有什么特殊的位置?请你给它起一个名字,并描述这一位置的特征.
相等
点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点.
活动探究
把一条线段分成两条相等的线段的点,叫做这条线段的中点.又叫做二等分点.
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC.
归纳
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
例题讲解
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
例题讲解
变式训练
1.下列说法不正确的是( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB2.如果线段AB=13 cm,MA+MB=17 cm,那么下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
课后练习
A
D
3.如图,下列关系式中与图形不符合的是( )
A. AD-CD=AB+BC
B. AC-BC=AD-BD
C. AC-BC=AC+BD
D. AD-AC=BD-BC
4.在直线l上顺次取A,B,C三点,使得AB=5 cm,BC=3 cm.如果O是线段AC的中点,那么线段OB的长度是( )
A. 0.5 cm B. 1 cm C. 1.5 cm D. 2 cm
课后练习
C
B
5.下列四个图中,能表示线段x=a+c-b的是( )
课后练习
D
6.关于A,B,C三点,有下列几种说法:①若点C在线段AB上,则AC+BC=AB;②若点C在线段AB所在的直线上,则CB>AC;③若AC+BC>AB,则点C在线段AB外;④若点C是线段AB的中点,则AB=2BC.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
课后练习
C
7.已知数轴上有A,B,C三点,它们所表示的数分别是2,-4,x.
(1)求线段AB的长度;
(2)若AC=5,求x的值.
【解】 (1)AB=2-(-4)=6.
(2)2-x=5,x=-3或x-2=5,x=7.
课后练习
1、线段的和差实质是线段长度的和差,因此线段间的数量关系就是长度上的数量关系.
2、理解中点的意义和寻找线段间的和差倍分关系是解决线段计算类问题的关键 .
3、用代数设元是解决线段和差问题的一种重要思想.
4、当点之间的相对位置不明确时,应进行分类讨论.
课后总结
6.如图,A,B,C,D表示四个村庄,村民们准备合打一口水井.
(1) 水井的位置现有P,Q两种选择方案. 点P在线段BD上,点Q在线段AB上.哪一种方案的水井到各村庄的距离总和较小?
(2) 你能给出一种使水井到各村庄的距离之和最小的方案吗? 若能,请标出水井的位置,并说明理由.
(1) 可以用测量或比较线段长短的方法得到.选点P,水井到各村庄距离总和较小.
(2)当打井的位置选在AC与BD的交点时,水井到各村庄的距离之和最小,根据"两点之间线段最短".
作业题
感
谢
看
观
6.4??线段的和差
1、比较线段长短的方法:度量法和叠合法
2、用尺规作线段等于已知线段
3、基本实事:两点之间线段最短
4、两点之间的距离是连接两点的线段的长度
知识回顾
教学目标:
1.理解线段的和差的意义.
2.会用直尺和圆规作两条线段的和与差.
3.理解线段的中点的概念,会用刻度尺二等分一条线段.
4.会进行有关线段的和、差、倍、分的简单计算.
重难点:
●本节教学的重点是线段的和差的概念,这是相关作图和计算的依据.
●例2涉及较多的线段和较复杂的数量关系,是本节教学中的难点.
目标难点
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
导入新课
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
新课讲解
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
归纳
如图,C是线段AB上的一点,请完成下面的填空.
(1)AC+CB=___________;
(2)AB-CB=___________;
(3)BC=__________-AC.
AB
AC
AB
做一做
A
C
B
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
21世纪教育网
例题讲解
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
例题讲解
如图,已知线段a,b,c,用直尺和圆规画线段,使得:
(1)AB=a-b;(2)OF=a-2b+c.
【解】 (1)画法:①画射线AM;
②在射线AM上截取AB=a,在线段AB的反方向截取BC=b;
线段AC就是所求的线段a-b.如解图①.
(2)画法:①画射线ON;
②在射线ON上依次截取OD=a,DE=c;
③在线段OE的反方向截取EF=2b.
线段OF就是所求的线段a-2b+c.如解图②.
变式训练
拿出一张白纸,对折这张白纸.把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
点C具有什么特殊的位置?请你给它起一个名字,并描述这一位置的特征.
相等
点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点.
活动探究
把一条线段分成两条相等的线段的点,叫做这条线段的中点.又叫做二等分点.
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC.
归纳
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
例题讲解
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
例题讲解
变式训练
1.下列说法不正确的是( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
课后练习
A
D
3.如图,下列关系式中与图形不符合的是( )
A. AD-CD=AB+BC
B. AC-BC=AD-BD
C. AC-BC=AC+BD
D. AD-AC=BD-BC
4.在直线l上顺次取A,B,C三点,使得AB=5 cm,BC=3 cm.如果O是线段AC的中点,那么线段OB的长度是( )
A. 0.5 cm B. 1 cm C. 1.5 cm D. 2 cm
课后练习
C
B
5.下列四个图中,能表示线段x=a+c-b的是( )
课后练习
D
6.关于A,B,C三点,有下列几种说法:①若点C在线段AB上,则AC+BC=AB;②若点C在线段AB所在的直线上,则CB>AC;③若AC+BC>AB,则点C在线段AB外;④若点C是线段AB的中点,则AB=2BC.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
课后练习
C
7.已知数轴上有A,B,C三点,它们所表示的数分别是2,-4,x.
(1)求线段AB的长度;
(2)若AC=5,求x的值.
【解】 (1)AB=2-(-4)=6.
(2)2-x=5,x=-3或x-2=5,x=7.
课后练习
1、线段的和差实质是线段长度的和差,因此线段间的数量关系就是长度上的数量关系.
2、理解中点的意义和寻找线段间的和差倍分关系是解决线段计算类问题的关键 .
3、用代数设元是解决线段和差问题的一种重要思想.
4、当点之间的相对位置不明确时,应进行分类讨论.
课后总结
6.如图,A,B,C,D表示四个村庄,村民们准备合打一口水井.
(1) 水井的位置现有P,Q两种选择方案. 点P在线段BD上,点Q在线段AB上.哪一种方案的水井到各村庄的距离总和较小?
(2) 你能给出一种使水井到各村庄的距离之和最小的方案吗? 若能,请标出水井的位置,并说明理由.
(1) 可以用测量或比较线段长短的方法得到.选点P,水井到各村庄距离总和较小.
(2)当打井的位置选在AC与BD的交点时,水井到各村庄的距离之和最小,根据"两点之间线段最短".
作业题
感
谢
看
观
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
