6.6 角的大小比较 课件(共22张PPT)
文档属性
| 名称 | 6.6 角的大小比较 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:49:29 | ||
图片预览






文档简介
第6章 图形的初步知识
6.6??角的大小比较
由两条公共端点的射线所组成的图形.
由一条射线绕着它的端点旋转而成的图形.
1、用三个大写字母表示,表示顶点 的字母写在 中间;
2、用一个顶点的字母 来表示 ,顶 点处只有一个字母;
3、用一个数字或希腊字母字母表示,要加弧线.
角的定义:
角的表示方法:
角的度量:
1°=60 ′, ;1 ′=60 ″, .
知识回顾
教学目标:
1.理解角的大小的概念.
2.会用度量法比较两个角的大小,了解比较两个角的大小的叠合方法.
3.理解角的分类.
4.会用量角器作一个角等于已知角.
重难点:
●本节教学的重点是角的大小比较的概念和方法.
●由于还没有学习过用尺规作一个角等于已知角,这就给理解、运用叠合法比较两个角的大小带来一定的困难, 用叠合法比较两个角的大小是本节教学的难点.
目标难点
8:00与5:00这两个时刻,时针与分针所成的角哪个较大?你是怎样比较的?
导入新课
一般地,如果两个角的度数相等,那么我们就说这两个角相等.例如下图中,∠B与∠C相等,记做∠B=∠C .如果两个角的度数不相等,那么我们就说度数较大的角较大.例如下图中, ∠B大于∠A,记做∠B>∠A;也可以说成∠A小于∠B,记做∠A<∠B .
新课讲解
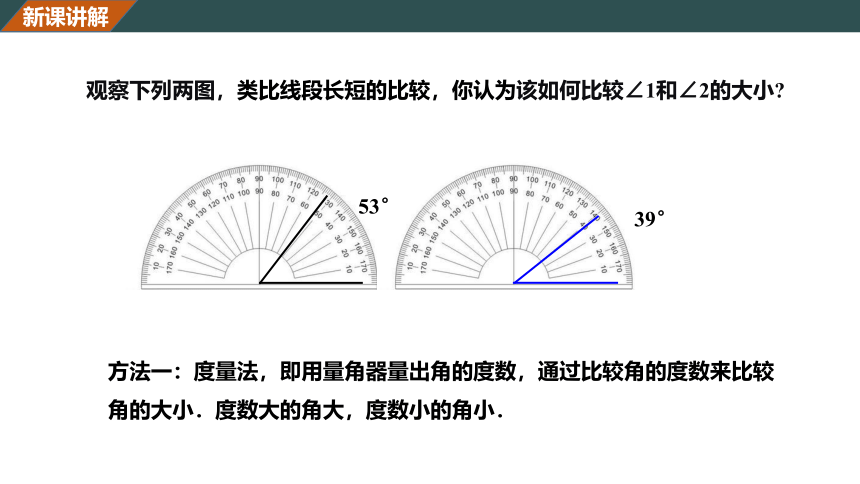
观察下列两图,类比线段长短的比较,你认为该如何比较∠1和∠2的大小?
53°
39°
方法一:度量法,即用量角器量出角的度数,通过比较角的度数来比较角的大小.度数大的角大,度数小的角小.
新课讲解
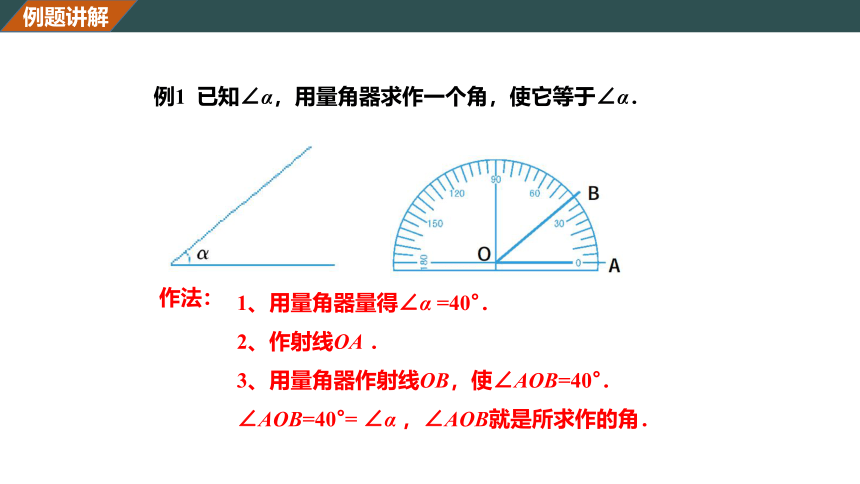
例1 已知∠α,用量角器求作一个角,使它等于∠α.
作法:
1、用量角器量得∠α =40°.
2、作射线OA .
3、用量角器作射线OB,使∠AOB=40°.
∠AOB=40°= ∠α ,∠AOB就是所求作的角.
例题讲解
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
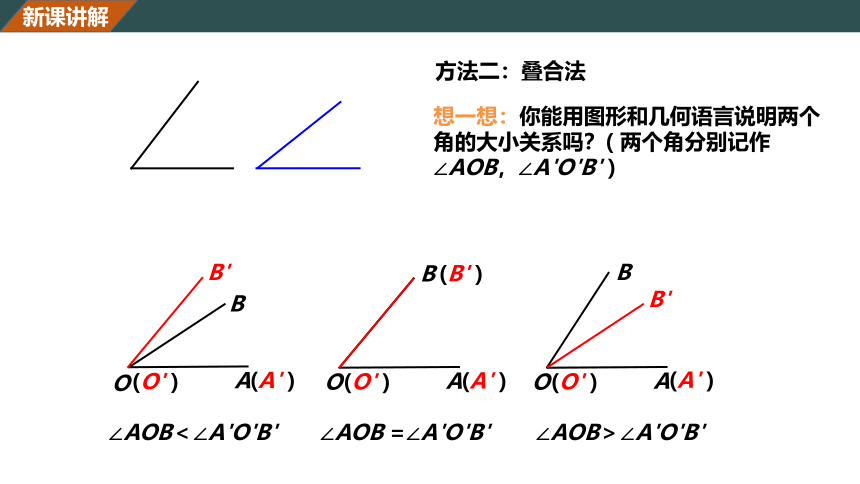
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
方法二:叠合法
新课讲解
方法二:叠合法.把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.如下图:
新课讲解
如图把一块三角尺中的∠BAC与另一块三角尺的∠QPO叠放在一起,使顶点A与P重合,角边AC与角边PO重合,并使两个角的另一边AB与PQ都在重合的一边的同侧.此时,AB边落在∠QPO的内部,表明∠BAC的度数小于∠QPO的度数,即∠BAC< ∠QPO .如果把两个角叠在一起时,能使它们的两条角边都重合,就表明这两个角度数相等,即这两个角相等.
新课讲解
叠合法从“形”上比较,
度量法从“数”上比较,
不管用哪种方法比较,结果都是一致的.
注意:1、角的大小只与开口大小有关,与边的长短无关,书写时注意角的符号与小于号、大于号的区别.
2、叠合法把两个角的顶点和一条边重合,并使两个角的另一条边在重合边的同侧,再通过观察两个角的另一边的位置进行判断.
归纳
等于90°的角是直角.小于直角的角是锐角.大于直角而小于平角的角是钝角.
下列角分别为哪类角?
锐角
直角
钝角
锐角
钝角
新课讲解
{5940675A-B579-460E-94D1-54222C63F5DA}角
定义
∠α的范围
图示
锐角
直角
钝角
平角
周角
小于直角的角
等于90°的角
大于直角而小于平角的角
等于180°的角
等于360°的角
0°<∠α<90 °
∠α=90 °
90°<∠α<180 °
∠α=180 °
∠α=360 °
归纳
例2 如图,点A、O、E在一条直线上,∠AOC=90°,∠BOD =90°, 解答下列问题:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小.
(2)找出图中的直角、锐角和钝角.
解:(1)由右图可以看出: ∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE .
(2)图中的直角有∠AOC,∠BOD ,∠ COE;
锐角有∠ AOB, ∠ BOC,∠ COD,∠ DOE;
钝角有∠ AOD,∠ BOE.
例题讲解
变式练习
如图,∠BOD=90°,∠COE=90°,解答下列问题:
(1)图中有哪些小于平角的角?用适当的方法表示出它们.
(2)比较∠AOC、∠AOD、∠AOE、∠AOB的大小,并指出其中的锐角、钝角、直角、平角.
(1)∠AOC、∠AOD、∠AOE、∠COD、∠COE、∠DOE、∠DOB、∠EOB;(2)∠AOC<∠AOD<∠AOE<∠AOB,其中∠AOC为锐角,∠AOD为直角,∠AOE为钝角,∠AOB为平角。
1. 下列说法错误的是( )
A. 角的大小与角的边的长短没有关系
B. 角的大小与它们的度数大小是一致的
C. 用叠合法比较两个角的大小,只要把两个角的顶点和任意一边重合即可
D. 用度量法比较两个角的大小,只要把两个角的度数量出,比较度数的大小即可
课后练习
C
2. 若∠A与∠B的和是一个钝角,那么( )
A. ∠A与∠B都是锐角 B. ∠A与∠B都是直角
C. ∠A与∠B一个锐角一个直角 D. 不可能都是钝角
课后练习
3.用一个放大镜去考查一个角的大小,正确的说法是( )
A.角的度数扩大了 B.角的度数缩小了
C.角的度数没有变化 D.以上都不对
D
C
4.如图所示,小于平角的角有( )
A.9个 B.8个 C.7个 D.6个
【解析】符合条件的角中以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,故有1+2+1+1+2=7个角.故选C.
课后练习
C
5.根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为________.
解:由图可观察出:∠BOC<∠BOD; ∠COD<∠BOD;
∠AOD最大;
∠AOC=∠BOD=90度.
故∠BOC<∠COD<∠AOC=∠BOD=90°<∠AOD.
课后练习
6.如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求:2·1·c·n·j·y
(1)∠DBA<∠DBC;
(2)∠DBA>∠DBC;
(3)∠DBA=∠DBC.
(1)∠DBA是锐角时;(2)∠DBA是钝角时;(3)∠DBA是直角时
【解析】因为钝角>直角>锐角,所以可得:
(1)当∠DBA是锐角时,∠DBC是钝角,可满足∠DBA<∠DBC;
(2)当∠DBA是钝角时,∠DBC是锐角,可满足∠DBA>∠DBC;
(3)当∠DBA是直角时,∠DBA=∠DBC=90°,可满足∠DBA=∠DBC.
课后练习
1、比较角的大小的方法:
方法一:度量法,即用量角器量出角的度数,通过比较角的度数来比较角的大小.度数大的角大,度数小的角小.
方法二:叠合法.把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.
2、角的分类:
锐角、直角、钝角、平角、周角.
课后总结
感
谢
看
观
6.6??角的大小比较
由两条公共端点的射线所组成的图形.
由一条射线绕着它的端点旋转而成的图形.
1、用三个大写字母表示,表示顶点 的字母写在 中间;
2、用一个顶点的字母 来表示 ,顶 点处只有一个字母;
3、用一个数字或希腊字母字母表示,要加弧线.
角的定义:
角的表示方法:
角的度量:
1°=60 ′, ;1 ′=60 ″, .
知识回顾
教学目标:
1.理解角的大小的概念.
2.会用度量法比较两个角的大小,了解比较两个角的大小的叠合方法.
3.理解角的分类.
4.会用量角器作一个角等于已知角.
重难点:
●本节教学的重点是角的大小比较的概念和方法.
●由于还没有学习过用尺规作一个角等于已知角,这就给理解、运用叠合法比较两个角的大小带来一定的困难, 用叠合法比较两个角的大小是本节教学的难点.
目标难点
8:00与5:00这两个时刻,时针与分针所成的角哪个较大?你是怎样比较的?
导入新课
一般地,如果两个角的度数相等,那么我们就说这两个角相等.例如下图中,∠B与∠C相等,记做∠B=∠C .如果两个角的度数不相等,那么我们就说度数较大的角较大.例如下图中, ∠B大于∠A,记做∠B>∠A;也可以说成∠A小于∠B,记做∠A<∠B .
新课讲解
观察下列两图,类比线段长短的比较,你认为该如何比较∠1和∠2的大小?
53°
39°
方法一:度量法,即用量角器量出角的度数,通过比较角的度数来比较角的大小.度数大的角大,度数小的角小.
新课讲解
例1 已知∠α,用量角器求作一个角,使它等于∠α.
作法:
1、用量角器量得∠α =40°.
2、作射线OA .
3、用量角器作射线OB,使∠AOB=40°.
∠AOB=40°= ∠α ,∠AOB就是所求作的角.
例题讲解
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
方法二:叠合法
新课讲解
方法二:叠合法.把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.如下图:
新课讲解
如图把一块三角尺中的∠BAC与另一块三角尺的∠QPO叠放在一起,使顶点A与P重合,角边AC与角边PO重合,并使两个角的另一边AB与PQ都在重合的一边的同侧.此时,AB边落在∠QPO的内部,表明∠BAC的度数小于∠QPO的度数,即∠BAC< ∠QPO .如果把两个角叠在一起时,能使它们的两条角边都重合,就表明这两个角度数相等,即这两个角相等.
新课讲解
叠合法从“形”上比较,
度量法从“数”上比较,
不管用哪种方法比较,结果都是一致的.
注意:1、角的大小只与开口大小有关,与边的长短无关,书写时注意角的符号与小于号、大于号的区别.
2、叠合法把两个角的顶点和一条边重合,并使两个角的另一条边在重合边的同侧,再通过观察两个角的另一边的位置进行判断.
归纳
等于90°的角是直角.小于直角的角是锐角.大于直角而小于平角的角是钝角.
下列角分别为哪类角?
锐角
直角
钝角
锐角
钝角
新课讲解
{5940675A-B579-460E-94D1-54222C63F5DA}角
定义
∠α的范围
图示
锐角
直角
钝角
平角
周角
小于直角的角
等于90°的角
大于直角而小于平角的角
等于180°的角
等于360°的角
0°<∠α<90 °
∠α=90 °
90°<∠α<180 °
∠α=180 °
∠α=360 °
归纳
例2 如图,点A、O、E在一条直线上,∠AOC=90°,∠BOD =90°, 解答下列问题:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小.
(2)找出图中的直角、锐角和钝角.
解:(1)由右图可以看出: ∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE .
(2)图中的直角有∠AOC,∠BOD ,∠ COE;
锐角有∠ AOB, ∠ BOC,∠ COD,∠ DOE;
钝角有∠ AOD,∠ BOE.
例题讲解
变式练习
如图,∠BOD=90°,∠COE=90°,解答下列问题:
(1)图中有哪些小于平角的角?用适当的方法表示出它们.
(2)比较∠AOC、∠AOD、∠AOE、∠AOB的大小,并指出其中的锐角、钝角、直角、平角.
(1)∠AOC、∠AOD、∠AOE、∠COD、∠COE、∠DOE、∠DOB、∠EOB;(2)∠AOC<∠AOD<∠AOE<∠AOB,其中∠AOC为锐角,∠AOD为直角,∠AOE为钝角,∠AOB为平角。
1. 下列说法错误的是( )
A. 角的大小与角的边的长短没有关系
B. 角的大小与它们的度数大小是一致的
C. 用叠合法比较两个角的大小,只要把两个角的顶点和任意一边重合即可
D. 用度量法比较两个角的大小,只要把两个角的度数量出,比较度数的大小即可
课后练习
C
2. 若∠A与∠B的和是一个钝角,那么( )
A. ∠A与∠B都是锐角 B. ∠A与∠B都是直角
C. ∠A与∠B一个锐角一个直角 D. 不可能都是钝角
课后练习
3.用一个放大镜去考查一个角的大小,正确的说法是( )
A.角的度数扩大了 B.角的度数缩小了
C.角的度数没有变化 D.以上都不对
D
C
4.如图所示,小于平角的角有( )
A.9个 B.8个 C.7个 D.6个
【解析】符合条件的角中以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,故有1+2+1+1+2=7个角.故选C.
课后练习
C
5.根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为________.
解:由图可观察出:∠BOC<∠BOD; ∠COD<∠BOD;
∠AOD最大;
∠AOC=∠BOD=90度.
故∠BOC<∠COD<∠AOC=∠BOD=90°<∠AOD.
课后练习
6.如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求:2·1·c·n·j·y
(1)∠DBA<∠DBC;
(2)∠DBA>∠DBC;
(3)∠DBA=∠DBC.
(1)∠DBA是锐角时;(2)∠DBA是钝角时;(3)∠DBA是直角时
【解析】因为钝角>直角>锐角,所以可得:
(1)当∠DBA是锐角时,∠DBC是钝角,可满足∠DBA<∠DBC;
(2)当∠DBA是钝角时,∠DBC是锐角,可满足∠DBA>∠DBC;
(3)当∠DBA是直角时,∠DBA=∠DBC=90°,可满足∠DBA=∠DBC.
课后练习
1、比较角的大小的方法:
方法一:度量法,即用量角器量出角的度数,通过比较角的度数来比较角的大小.度数大的角大,度数小的角小.
方法二:叠合法.把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.
2、角的分类:
锐角、直角、钝角、平角、周角.
课后总结
感
谢
看
观
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
