6.9 直线的相交 课件(2课时 共29张PPT)
文档属性
| 名称 | 6.9 直线的相交 课件(2课时 共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 20:02:56 | ||
图片预览







文档简介
第6章 图形的初步知识
6.9??直线的相交
第1课时
1、什么叫做互为余角?
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.
互余的数学表达式:∠α +∠β = 90 °.
如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
互补的数学表达式为: ∠α+∠β =180 °.
2、什么叫做互为补角?
知识回顾
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
知识回顾
在生活中,我们会经常看到两条直线相交的情景.如图若把交叉的两条公路看成两条直线AB、CD ,则直线AB、CD相交于点O.
A
B
C
D
O
新课导入
我们知道,如果两条直线只有一个公共点,就说这两条直线相交,该公共点叫做这两条直线的交点.
数学描述:如图,直线 AB和CD相交,其交点是O点.
问题1:两直线相交时构成了几个角?表示出来.
答案1:
答案2:它们的顶点相同,角的两边互为反向延长线.
问题2: 与 及 与 分别有何联系?
新课讲解
对顶角的顶点相同,角的两边互为反向延长线.
特征
如图,直线AB与CD相交,其交点是O,∠1,∠2, ∠ AOD和∠COB是AB与CD相交所成的角.我们把其中相对的任何一对角: ∠1与∠2,或∠AOD与∠COB叫做对顶角.
新课讲解
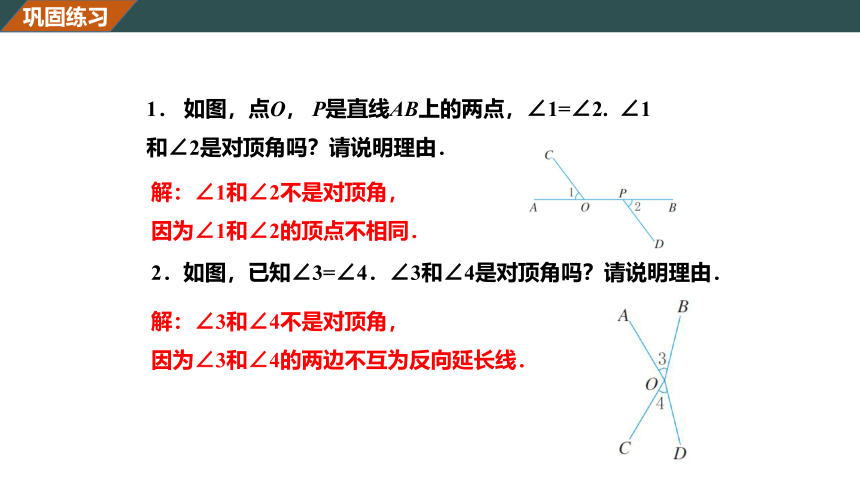
1. 如图,点O, P是直线AB上的两点,∠1=∠2. ∠1和∠2是对顶角吗?请说明理由.
解:∠1和∠2不是对顶角,
因为∠1和∠2的顶点不相同.
2.如图,已知∠3=∠4.∠3和∠4是对顶角吗?请说明理由.
解:∠3和∠4不是对顶角,
因为∠3和∠4的两边不互为反向延长线.
巩固练习
例1 如图三条直线相交于点O,说出图中的6组对顶角.
解:∠AOF与∠BOE,
∠FOD与∠EOC,
∠DOB与∠COA,
∠AOD与∠BOC,
∠FOB与∠EOA,
∠DOE与∠COF.
例题讲解
变式练习
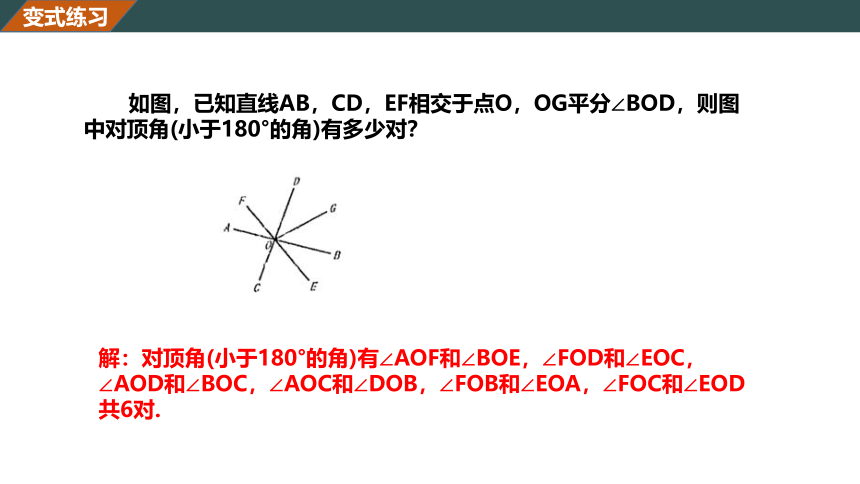
如图,已知直线AB,CD,EF相交于点O,OG平分∠BOD,则图中对顶角(小于180°的角)有多少对?
解:对顶角(小于180°的角)有∠AOF和∠BOE,∠FOD和∠EOC,∠AOD和∠BOC,∠AOC和∠DOB,∠FOB和∠EOA,∠FOC和∠EOD共6对.
如图,如果∠1=52°,那么∠2等于多少度?请说明理由.
解:∠2 =52°,
理由:∵∠1+∠AOD =180° ,
∠2+∠AOD =180° ,
∴∠1= ∠2 =52° .(同角的补角相等)
对于任意两个对顶角相等吗?为什么?
对于任意两个对顶角它们的补角相同,所以它们是相等的,根据“同角的补角相等”.
对顶角的性质:对顶角相等.
新课讲解
例2 如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
解:∵∠DOE与∠COE互余,(已知)
∴ ∠DOE+∠COE =90 ° ,(互余的定义)
∴ ∠DOE= 90 ° - ∠COE= 90 ° -62 ° =28 °.
又∵ ∠AOB与∠DOE是对顶角,(已知)
∴ ∠AOB=∠DOE ,(对顶角相等)
∴ ∠AOB=28 °.
例题讲解
1、相交线的概念.
2、对顶角的定义及判定条件.
3、对顶角的性质:对顶角相等.
4、利用学习过的有关事实解决实际问题,体会数学在生活中的应用.
(1)顶点相同,
(2)角的两边互为反向延长线.
21cnjy.com
课后总结
第6章 图形的初步知识
6.9??直线的相交
第2课时
把一张正方形纸片按下图方式折叠,得到∠1,∠1是什么角?
把这张纸片展开,如下图,AB、CD是两条折痕,相交于点O,则∠AOC、∠AOD、∠BOC、∠BOD与∠1有什么关系?它们是什么角?
新课导入
当两条直线相交所构成的四个角中有一个是直角时,我们就称这两条直线互相垂直,其中的一条直线叫做另一条的垂线,它们的交点叫做垂足.
如图AB与CD垂直,记做AB⊥CD(或CD⊥AB).如果用l,m表示这两条直线,那么直线l与m垂直,记做l⊥m,点O是垂足.
“⊥”是“垂直”的符号,而“ ”是图形中“垂直”(直角)的标记.
新课讲解
(1)∵AB⊥CD (已知),
∴∠AOC=∠BOC=∠AOD= ∠BOD=90°. (垂直的定义)
(2)∵∠BOC = Rt∠ (已知),
∴AB⊥CD(垂直的定义).
新课讲解
过点A 作 l 的垂线,你能作出来吗?每个图中你能作几条?
作法:
1、贴
2、靠
3、过
l
l
A
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
4、画
点A在直线上l
点A在直线外l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
B
新课讲解
P
A B
你会用量角器过点P画直线AB的垂线吗?
过直线AB上一点P画AB的垂线,可以画几条?
若点P在直线AB外呢?
垂线的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
新课讲解
例3 如图,直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠ COE的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
(垂直的定义)
∵∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
(对顶角相等)
例题讲解
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
解:∵ON⊥OM,
∴∠MON=90°,
∵OM平分∠AOC,∠AOC=70°,
∴∠CON=90°﹣35°=55°,
故选:B.
∴∠MOC=????????∠AOC=35°,
?
变式练习
如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答:点P与直线l上的点O距离最小.
测量法或叠合法验证.
根据圆的半径最短验证.
合作学习
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.垂线段PO的长度,就是点P到直线l的距离.
已知P是直线外的一点,过点P画直线l的垂线,交直线l于点O,则线段PO叫做点P到直线l的垂线段.
直线外一点与直线上各点连结的所有线段中,垂线段最短.也可简单地说成:垂线段最短.
合作学习
巩固练习
如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
垂直定义:两条直线相交所构成的四个角中有一个是直角.
垂线的画法:三角尺和量角器 .
垂直的表示方法:用符号“⊥”表示.
垂直的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
垂线段最短:直线外一点与直线上各点连结的所有线段中,垂线段最短.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
课后总结
课后练习
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选D.
2.如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150° B.130° C.100° D.90°
解:∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC,又已知∠AOD+∠BOC=100°,
∴∠AOD=50°.
∵∠AOD与∠AOC互为邻补角,
∴∠AOC=180°﹣∠AOD=180°﹣50°=130°.故选B.
课后练习
3.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
解:∵∠2和∠COE为对顶角 ∴∠2=∠COE=32° ∵∠1+∠COE+∠BOE=180° 即95°+32°+∠BOE=180° ∴∠BOE=53° 故答案为:53°。
课后练习
课后练习
解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
4.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
感
谢
看
观
6.9??直线的相交
第1课时
1、什么叫做互为余角?
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角.
互余的数学表达式:∠α +∠β = 90 °.
如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
互补的数学表达式为: ∠α+∠β =180 °.
2、什么叫做互为补角?
知识回顾
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
知识回顾
在生活中,我们会经常看到两条直线相交的情景.如图若把交叉的两条公路看成两条直线AB、CD ,则直线AB、CD相交于点O.
A
B
C
D
O
新课导入
我们知道,如果两条直线只有一个公共点,就说这两条直线相交,该公共点叫做这两条直线的交点.
数学描述:如图,直线 AB和CD相交,其交点是O点.
问题1:两直线相交时构成了几个角?表示出来.
答案1:
答案2:它们的顶点相同,角的两边互为反向延长线.
问题2: 与 及 与 分别有何联系?
新课讲解
对顶角的顶点相同,角的两边互为反向延长线.
特征
如图,直线AB与CD相交,其交点是O,∠1,∠2, ∠ AOD和∠COB是AB与CD相交所成的角.我们把其中相对的任何一对角: ∠1与∠2,或∠AOD与∠COB叫做对顶角.
新课讲解
1. 如图,点O, P是直线AB上的两点,∠1=∠2. ∠1和∠2是对顶角吗?请说明理由.
解:∠1和∠2不是对顶角,
因为∠1和∠2的顶点不相同.
2.如图,已知∠3=∠4.∠3和∠4是对顶角吗?请说明理由.
解:∠3和∠4不是对顶角,
因为∠3和∠4的两边不互为反向延长线.
巩固练习
例1 如图三条直线相交于点O,说出图中的6组对顶角.
解:∠AOF与∠BOE,
∠FOD与∠EOC,
∠DOB与∠COA,
∠AOD与∠BOC,
∠FOB与∠EOA,
∠DOE与∠COF.
例题讲解
变式练习
如图,已知直线AB,CD,EF相交于点O,OG平分∠BOD,则图中对顶角(小于180°的角)有多少对?
解:对顶角(小于180°的角)有∠AOF和∠BOE,∠FOD和∠EOC,∠AOD和∠BOC,∠AOC和∠DOB,∠FOB和∠EOA,∠FOC和∠EOD共6对.
如图,如果∠1=52°,那么∠2等于多少度?请说明理由.
解:∠2 =52°,
理由:∵∠1+∠AOD =180° ,
∠2+∠AOD =180° ,
∴∠1= ∠2 =52° .(同角的补角相等)
对于任意两个对顶角相等吗?为什么?
对于任意两个对顶角它们的补角相同,所以它们是相等的,根据“同角的补角相等”.
对顶角的性质:对顶角相等.
新课讲解
例2 如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
解:∵∠DOE与∠COE互余,(已知)
∴ ∠DOE+∠COE =90 ° ,(互余的定义)
∴ ∠DOE= 90 ° - ∠COE= 90 ° -62 ° =28 °.
又∵ ∠AOB与∠DOE是对顶角,(已知)
∴ ∠AOB=∠DOE ,(对顶角相等)
∴ ∠AOB=28 °.
例题讲解
1、相交线的概念.
2、对顶角的定义及判定条件.
3、对顶角的性质:对顶角相等.
4、利用学习过的有关事实解决实际问题,体会数学在生活中的应用.
(1)顶点相同,
(2)角的两边互为反向延长线.
21cnjy.com
课后总结
第6章 图形的初步知识
6.9??直线的相交
第2课时
把一张正方形纸片按下图方式折叠,得到∠1,∠1是什么角?
把这张纸片展开,如下图,AB、CD是两条折痕,相交于点O,则∠AOC、∠AOD、∠BOC、∠BOD与∠1有什么关系?它们是什么角?
新课导入
当两条直线相交所构成的四个角中有一个是直角时,我们就称这两条直线互相垂直,其中的一条直线叫做另一条的垂线,它们的交点叫做垂足.
如图AB与CD垂直,记做AB⊥CD(或CD⊥AB).如果用l,m表示这两条直线,那么直线l与m垂直,记做l⊥m,点O是垂足.
“⊥”是“垂直”的符号,而“ ”是图形中“垂直”(直角)的标记.
新课讲解
(1)∵AB⊥CD (已知),
∴∠AOC=∠BOC=∠AOD= ∠BOD=90°. (垂直的定义)
(2)∵∠BOC = Rt∠ (已知),
∴AB⊥CD(垂直的定义).
新课讲解
过点A 作 l 的垂线,你能作出来吗?每个图中你能作几条?
作法:
1、贴
2、靠
3、过
l
l
A
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
4、画
点A在直线上l
点A在直线外l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
B
新课讲解
P
A B
你会用量角器过点P画直线AB的垂线吗?
过直线AB上一点P画AB的垂线,可以画几条?
若点P在直线AB外呢?
垂线的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
新课讲解
例3 如图,直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠ COE的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
(垂直的定义)
∵∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
(对顶角相等)
例题讲解
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
解:∵ON⊥OM,
∴∠MON=90°,
∵OM平分∠AOC,∠AOC=70°,
∴∠CON=90°﹣35°=55°,
故选:B.
∴∠MOC=????????∠AOC=35°,
?
变式练习
如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答:点P与直线l上的点O距离最小.
测量法或叠合法验证.
根据圆的半径最短验证.
合作学习
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.垂线段PO的长度,就是点P到直线l的距离.
已知P是直线外的一点,过点P画直线l的垂线,交直线l于点O,则线段PO叫做点P到直线l的垂线段.
直线外一点与直线上各点连结的所有线段中,垂线段最短.也可简单地说成:垂线段最短.
合作学习
巩固练习
如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
垂直定义:两条直线相交所构成的四个角中有一个是直角.
垂线的画法:三角尺和量角器 .
垂直的表示方法:用符号“⊥”表示.
垂直的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
垂线段最短:直线外一点与直线上各点连结的所有线段中,垂线段最短.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
课后总结
课后练习
1.平面内三条直线的交点个数可能有( )
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3个
解:如图所示,
分别有0个交点,1个交点,2个交点,3个交点,
∴交点个数可能有0个或1个或2个或3个.
故选D.
2.如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150° B.130° C.100° D.90°
解:∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC,又已知∠AOD+∠BOC=100°,
∴∠AOD=50°.
∵∠AOD与∠AOC互为邻补角,
∴∠AOC=180°﹣∠AOD=180°﹣50°=130°.故选B.
课后练习
3.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
解:∵∠2和∠COE为对顶角 ∴∠2=∠COE=32° ∵∠1+∠COE+∠BOE=180° 即95°+32°+∠BOE=180° ∴∠BOE=53° 故答案为:53°。
课后练习
课后练习
解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
4.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
感
谢
看
观
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
