名师导学——2.5 直角三角形

登陆21世纪教育 助您教考全无忧
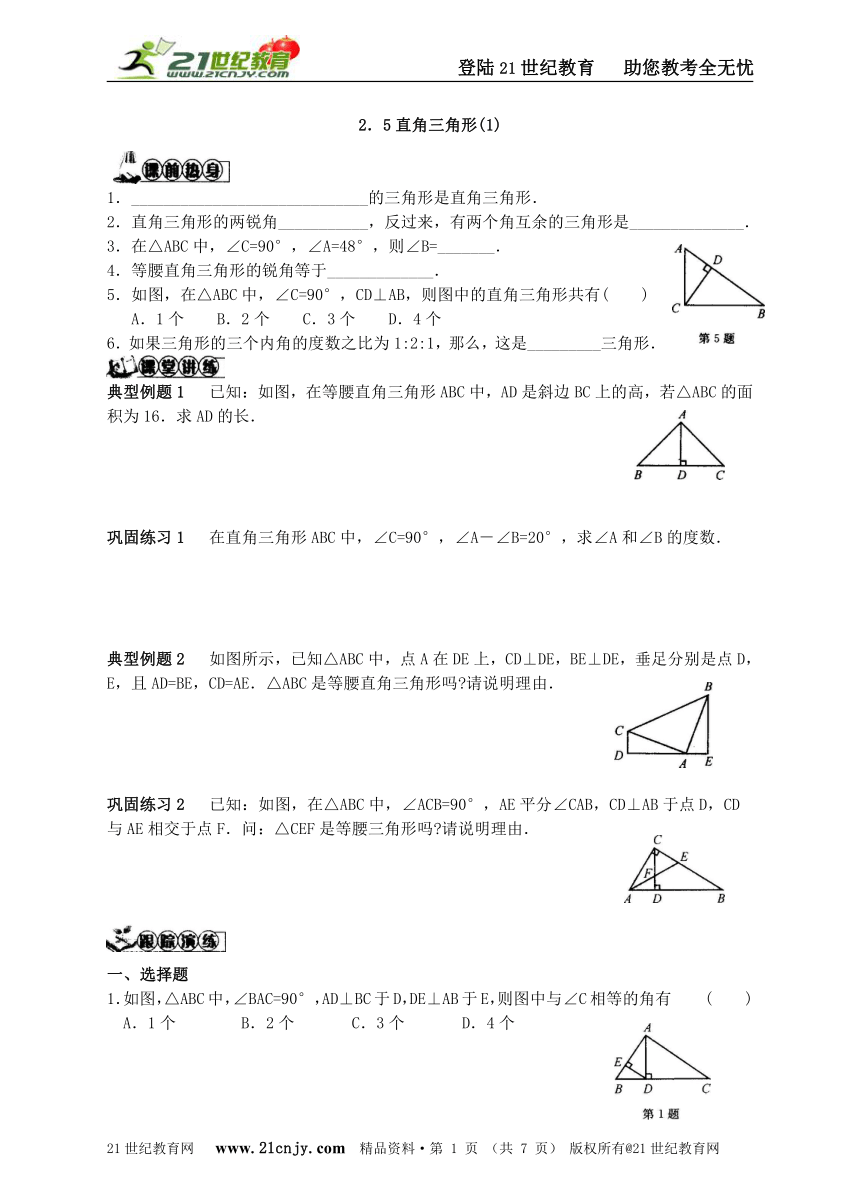
2．5直角三角形(1)
1．_____________________________的三角形是直角三角形．
2．直角三角形的两锐角___________，反过来，有两个角互余的三角形是______________．
3．在△ABC中，∠C=90°，∠A=48°，则∠B=_______．
4．等腰直角三角形的锐角等于_____________．
5．如图，在△ABC中，∠C=90°，CD⊥AB，则图中的直角三角形共有( )
A．1个 B．2个 C．3个 D．4个
6．如果三角形的三个内角的度数之比为1:2:1，那么，这是_________三角形．
典型例题1 已知：如图，在等腰直角三角形ABC中，AD是斜边BC上的高，若△ABC的面积为16．求AD的长．
巩固练习1 在直角三角形ABC中，∠C=90°，∠A－∠B=20°，求∠A和∠B的度数．
典型例题2 如图所示，已知△ABC中，点A在DE上，CD⊥DE，BE⊥DE，垂足分别是点D，E，且AD=BE，CD=AE．△ABC是等腰直角三角形吗 请说明理由．
巩固练习2 已知：如图，在△ABC中，∠ACB=90°，AE平分∠CAB，CD⊥AB于点D，CD与AE相交于点F．问：△CEF是等腰三角形吗 请说明理由．
一、选择题
1．如图，△ABC中，∠BAC=90°，AD⊥BC于D，DE⊥AB于E，则图中与∠C相等的角有 ( )
A．1个 B．2个 C．3个 D．4个
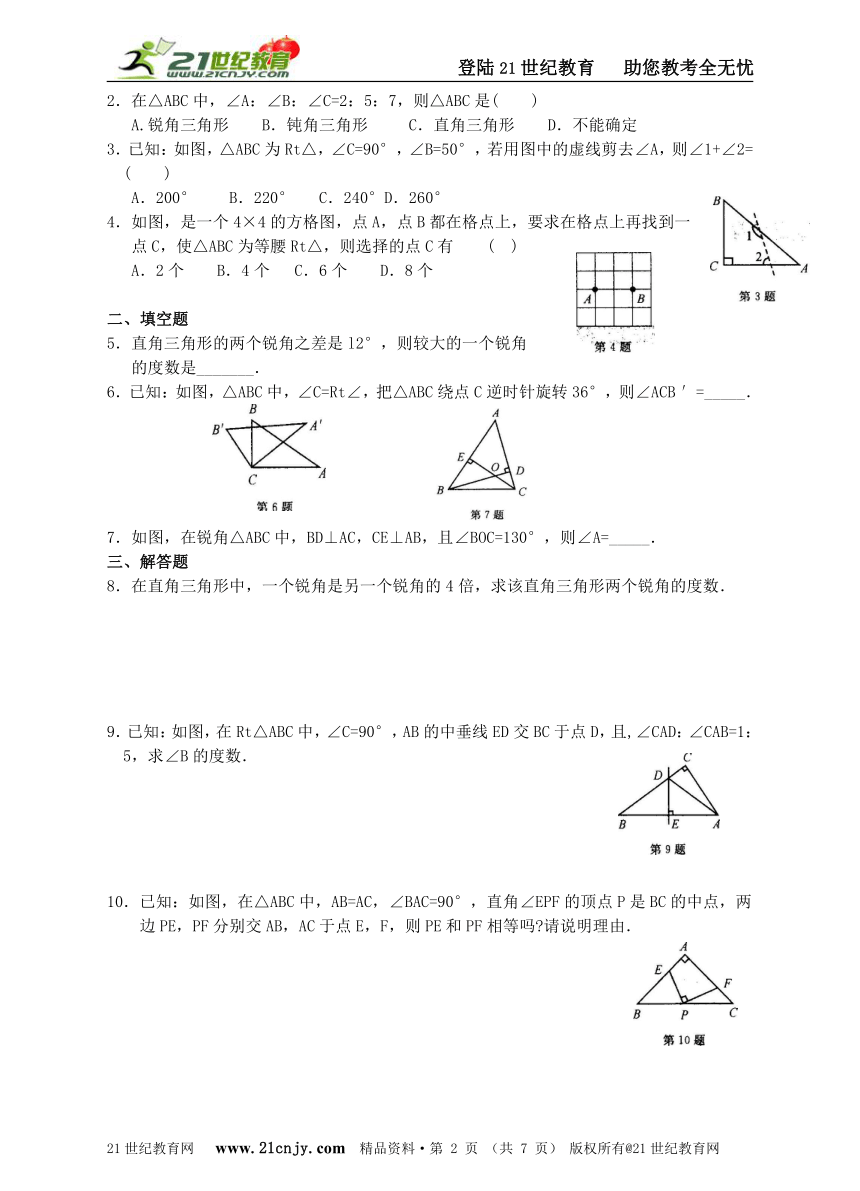
2．在△ABC中，∠A：∠B：∠C=2：5：7，则△ABC是( )
A.锐角三角形 B．钝角三角形 C．直角三角形 D．不能确定
3．已知：如图，△ABC为Rt△，∠C=90°，∠B=50°，若用图中的虚线剪去∠A，则∠1+∠2= ( )
A．200° B．220° C．240°D．260°
4．如图，是一个4×4的方格图，点A，点B都在格点上，要求在格点上再找到一点C，使△ABC为等腰Rt△，则选择的点C有 ( )
A．2个 B．4个 C．6个 D．8个
二、填空题
5．直角三角形的两个锐角之差是l2°，则较大的一个锐角
的度数是_______．
6．已知：如图，△ABC中，∠C=Rt∠，把△ABC绕点C逆时针旋转36°，则∠ACB ′=_____．
7．如图，在锐角△ABC中，BD⊥AC，CE⊥AB，且∠BOC=130°，则∠A=_____．
三、解答题
8．在直角三角形中，一个锐角是另一个锐角的4倍，求该直角三角形两个锐角的度数．
9．已知：如图，在Rt△ABC中，∠C=90°，AB的中垂线ED交BC于点D，且,∠CAD：∠CAB=1：5，求∠B的度数．
10．已知：如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，则PE和PF相等吗 请说明理由．
2．5直角三角形(2)
1．直角三角形斜边上的_________等于斜边的_____________．
2．在直角三角形中，如果一个角等于30°，则它所对的直角边等于斜边的_____________．
3．如图，在Rt△ABC中，∠C=90°，D是AB的中点，CD=3，则AB=________．
4．如图，在Rt△ABC中，∠C=90°，D是AB的中点，则图中等腰三角形有 ．
5．如图，CD是Rt△ABC斜边AB上的中线，CE是AB边上的高，∠A=26°，则∠DCE=________.
典型例题1 如图，△ABD和△ABC中，∠ACB=∠ADB=Rt∠，E是AB边上的中点，请你说明CE=DE的理由．
巩固练习1 已知：如图，在Rt△ABC中，CD是斜边AB上的中线，DE是△ACD的中线，则DE∥BC，请说明理由．
典型例题2 如图所示，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F，则BF=2CF，请说明理由．
巩固练习2 如图，在△ABC中，∠ACB=90°，BC=5，D是AB的中点，△BCD的周长是l8，则AB的长是_______.
一、选择题
1．把等边三角形ABC一边AB延长一倍到D，则△ADC是 ( )
A．等腰三角形 B．直角三角形 C．等边三角形 D．不能确定
2．如图，在△ABC中，∠B=∠C，AD是BC边上的中线，E为AB的中点，AC=6，则DE= ( )
A．2 B．3 C．4 D．6
3．如图，在△ABC中，AB=AC，∠BAC=4∠B，AD⊥AC，垂足为A，则∠ADC的度数为 ( )
A．30° B．45° C．60° D．75°
4．如图，在Rt△ABC中，∠B=90°，∠ACB=60°，延长BC到点D，使
CD=AC，则AC与BD的长度之比为( )
A．1：1 B．3：1 C．4：1 D．2：3
二、填空题
5．如图，在Rt△ABC中，CD是斜边AB的中线，∠BDC=110°，则∠A=_____，∠B=______．
6. 在△ABC中，∠A：∠B：∠C=1：2：3，BC=4，那∠AB=_______．
7. 已知等腰直角三角形的斜边长为8，则该三角形的面积为_________．
三、解答题
8．如图，在△ABC中，AB=AC=2a，∠ABC=∠ACB=15°，CD是腰AB上的高，求CD的长．
9．如图，在△ABC中，∠=90°，∠ABC=60°，BD平分∠ABC，若AD=6， 求CD的长.
10．如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的中线，DE⊥AC，则BC=2DE，试说明理由．
2．5提高班习题精选
1．已知，如图，CD是Rt△ABC的斜边AB上的中线，若∠A=35°，则∠BCD为 ( )
A．35° B．55° C．65° D．75°
2．如图，在△ABC中，∠ACB=90°，CD⊥AB，∠B=60°，则AD= ( )
A．BD B．2BD C．3BD D．4BD
3．如图，在Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于点
E，EF∥AC，则下列结论中一定成立的是 ( )
A．AB=BF B．AE=ED C．AD=DC D．∠ABE=∠DFE
4．在△ABC中，AB=AC=6，∠A=30°，则△ABC的面积为______.
5．如图，已知∠BAC=90°，AC=30°，AD⊥BC于D，DE⊥AB于E，BE=1，则BC=______．
6．如图，在△ABC中，∠B=40°，∠C=20°，AD⊥AC，垂足为A，交BC于D，若AB=4，则CD=_______．
7．如图，已知Rt△ABC中，∠C=90°，∠A=30°，AC=10，沿DE折叠，使得点A与点B重合，则折痕DE的长为_________．
8．如图，在Rt△ABC中，∠A=90°，AB=AC，D为BC的中点，E，F分别为AB，AC上的点，且BE=AF，则△DEF为等腰直角三角形，请说明理由．
9．如图，把直角三角形分成4个面积相等的直角三角形，用两种不同的方法，并标上相应的线段或角度标志．
10．如图，在Rt△ABC中，CD，CE分别是斜边AB上的高线和中线，CF是∠ACB的平分线，试说明CF是∠DCE的平分线的理由．
1．【2010·山西】在Rt△ABC中，∠ACB=90°，D是AB的中点，CD=4cm，则AB=_______cm．
2．【2009·温州】如图，在△ABC中，AB=AC=6，BC=8，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是 ( )
A．7+ B．10 C．4+2 D．12
参考答案
2．5直角三角形(1)
【课前热身】
1．有一个角是直角 2．互余 直角三角形 3．42° 4．45° 5．C 6．等腰直角三角形
【课堂讲练】
典型例题l 解：∵△ABC是等腰Rt△，AD⊥BC ∴AD=BD=CD ∵S△ABC=l6 ∴=16即AD2=16 ∵AD＞0 ∴AD=4
巩固练习l 解：∵△ABC为直角三角形且∠C=90°∴∠A+∠B=90° ∵∠A-∠B=20° ∴2∠A=110°即∠A=55°∠B=35°
典型例题2 解：∵CD⊥DE BE⊥DE ∴∠D=∠E=90° ∵AD=BE CD=AE ∴△ACD≌△BAE ∴∠DAC=∠EBA AC=AB ∵∠BAE+∠EBA=90°∴∠DAC+∠BAE=90° ∴∠CAB=90° ∴△ABC是等腰直角三角形
巩固练习2 解：△CEF是等腰三角形，理由：∵AE平分∠CAB ∴∠l=∠2 ∵CD⊥AB ∴∠2+
∠AFD=90°∵∠ACB=90°∴∠1+∠AEC=90°∴∠AEC=∠AFD=∠CFE ∴△CEF是等腰△
【跟踪演练】
1．B 2．C 3．B 4．C 5．51° 6．126° 7．50° 8．解：设两锐角为x和4x 则x+4x=90°，x=18°∴两锐角分别为18°和72° 9．解：∵DE是AB的中垂线 ∴∠DBE=∠DAB ∵∠CAD：∠CAB=1：5 ∴设∠CAD=x 则∠DAB=4x ∵∠C=90° ∴∠B+∠BAC=90°得4x+5x=90°∴x=10°∴∠B=4x=40° l0．解：PE=PF，理由：连结AP，由∠EAP=∠C=45°AP=CP
∠APE=∠CPF，得△AEP≌△CFP ∴PE=PF
2．5直角三角形(2)
【课前热身】
1．中线 一半 2．一半 3．6 4．△ACD和△BCD 5．38°
【课堂讲练】
典型例题l 解：在Rt△ABC和Rt△ABD中，∠ACB=∠ADB=90°，E是AB边上的中点，∴CE=AB，DE=AB ∴CE=DE
巩固练习l 解：在Rt△ABC中 ∵CD是斜边上的中线 ∴CD=AB=AD ∴△ACD是等腰三角形 ∵DE是△ACD的中线 ∴DE⊥AC(等腰三角形三线合一) 又∵BC⊥AC ∴DE∥BC
典型例题2 解：连结AF, ∵AB=AC ∠BAC=120°∴∠B=∠C=30°∵EF为AC中垂线 可
得AF=CF ∴∠CAF=30°∴∠BAF=90°∵∠B=30°∴BF=2AF=2CF
巩固练习2 13
【跟踪演练】
1．B 2．B 3．C 4．D 5．55°35°6．8 7．16 8．解：∵AB=AC=2a ∠ABC=∠ACB=15°∴∠DAC=30°∴CD=AC=×2a =a
9．解：∵∠C=90°∠ABC=60°∴∠A=30°∵BD平分∠ABC∴∠ABD=∠CBD=30°∴AD=BD=6在Rt△BCD中，∵∠CBD=30°∴CD=BD=3 10．解：∵∠ACB=90°∠A=30°∴BC=AB 又∵CD是AB边上的中线 ∴AD=CD ∵DE⊥AC ∴DE=CD=AB ∴BC=2DE
2．5提高班习题精选
【提高训练】
1．B 2．C 3．A 4．9 5．8 6．8 7．10／3 8．解：连结AD，∵∠A=90°，AB=AC，D为BC的中点 ∴∠B=∠DAC=45°，BD=AD又∵BE=AF ∴△BED≌△AFD(SAS) ∴∠BDE=∠ADF，DE=DF 则∠EDF=∠ADE+∠ADF=∠ADE+∠BDE=∠ADB=90°∴△DEF为等腰Rt△ 9.
10．解：∵∠ACD=∠B，∠ECB=∠B ∴∠ACD=∠ECB ∵∠ACF=∠BCF
∴∠ACF-∠ACD=∠BCF=∠ECB，即∠FCD=∠ECF ∴CF是∠DCE的平分线
【中考链接】
1．8 2．B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 （共 7 页） 版权所有@21世纪教育网