名师导学——2.6 探索勾股定理

登陆21世纪教育 助您教考全无忧
2．6探索勾股定理(1)
1．勾股定理：直角三角形两条直角边的________等于斜边的________．如果a，b为直角三角形的两条直角边长，c为斜边长，则__________________.
2．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，若a=3，b=4，则c=_____；若a=6，c=10，则b=_______．
3．正方形的边长为5，则该正方形的对角线长为_________．
4．如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=2，则直角边AC的长
为________.
5．在Rt△ABC中，∠C=90°，若两条直 角边a：b=3：4，斜边c=10， 则 △ABC 的面积为_________．
典型例题1 已知：在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为以，b，c．
(1)若a=30，c=50，求b；
(2)若a：b=8：15，c=34，求a．
巩固练习1 求出下列直角三角形中未知边的长度．
典型题例2 如图，在两墙之问有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点．已知∠BAC=60°，∠DAE=45°，点D到地面的垂直距离DE=3，求点B到地面的垂直距离BC的长度．
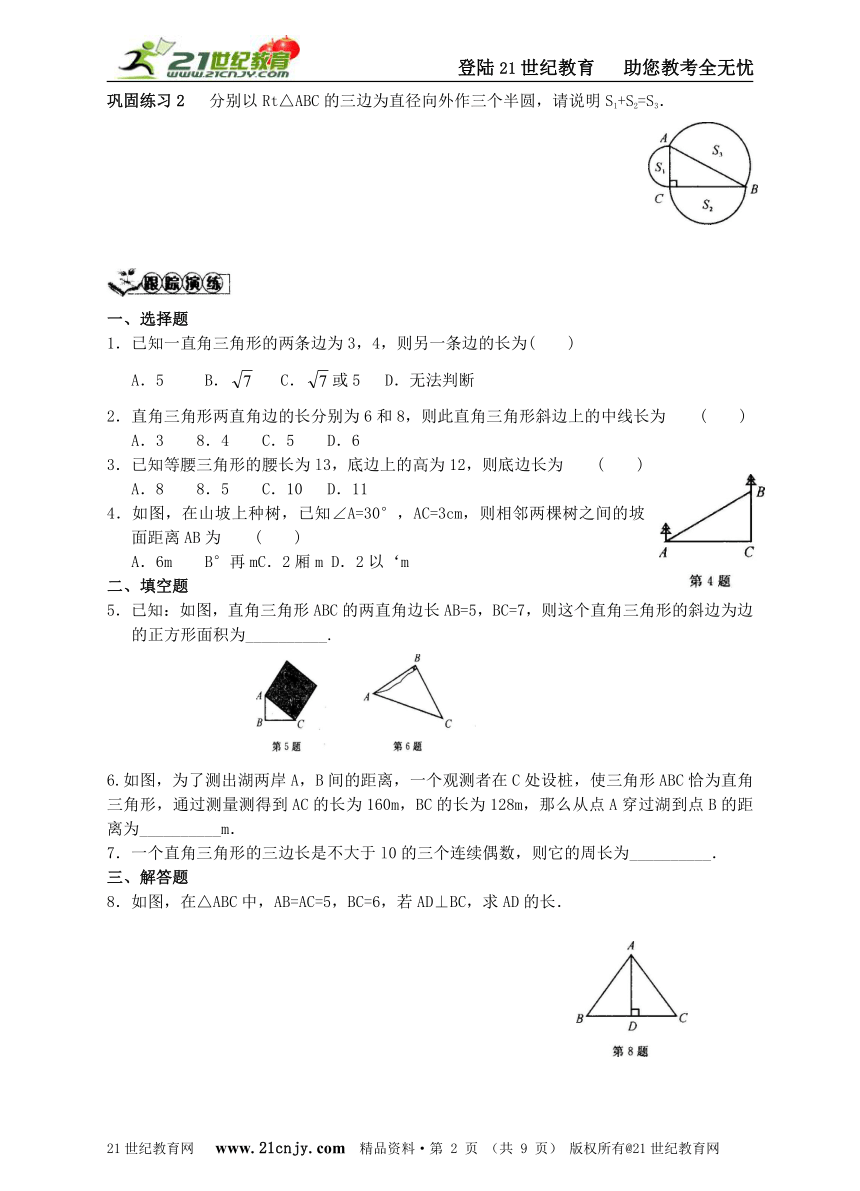
巩固练习2 分别以Rt△ABC的三边为直径向外作三个半圆，请说明S1+S2=S3．
一、选择题
1．已知一直角三角形的两条边为3，4，则另一条边的长为( )
A．5 B． C．或5 D．无法判断
2．直角三角形两直角边的长分别为6和8，则此直角三角形斜边上的中线长为 ( )
A．3 8．4 C．5 D．6
3．已知等腰三角形的腰长为l3，底边上的高为12，则底边长为 ( )
A．8 8．5 C．10 D．11
4．如图，在山坡上种树，已知∠A=30°，AC=3cm，则相邻两棵树之间的坡面距离AB为 ( )
A．6m B°再mC．2厢m D．2以‘m
二、填空题
5．已知：如图，直角三角形ABC的两直角边长AB=5，BC=7，则这个直角三角形的斜边为边的正方形面积为__________.
6.如图，为了测出湖两岸A，B间的距离，一个观测者在C处设桩，使三角形ABC恰为直角三角形，通过测量测得到AC的长为160m，BC的长为128m，那么从点A穿过湖到点B的距离为__________m．
7．一个直角三角形的三边长是不大于l0的三个连续偶数，则它的周长为__________．
三、解答题
8．如图，在△ABC中，AB=AC=5，BC=6，若AD⊥BC，求AD的长．
9．如图，一根旗杆在离地面9m处的C点断裂，旗杆顶部 落在离旗杆底部12m处，旗杆折断之前有多高
10．一架云梯长25m，斜靠在墙上，梯子顶端距地面的垂直高度为24m．
(1)梯子底端离墙多远
(2)如果梯子顶端下滑了4m，那么梯子底部在水平方向也滑动了4m吗 请通过计算加以说明．
2．6探索勾股定理(2)
1．如果三角形中两边的平方和等于第三边的______，那么这个三角形是________；且最大边所对的角是_____________．
2．若一个三角形的三条边分别为6cm，8cm，lOcm，则这个三角形是______________．
3．能够成为直角三角形三边长的三个正整数，称为勾股数，如3，4，5；6，8，10．请再列举两组勾股数_________、_______________.
4．一块三角形水稻田的三边长为5m，12m，13m，则这块稻田的面积为___________m2．
5．在△ABC中，a 2=(c+b)(c-b)，那么△ABC是______,c是_______边.
，f是 边．
典型例题1 根据下列条件，分别判断以以，b，C为边的三角形能否构成直角三角形．
(1)a=, b=，c=；
(2)a=1，b=，c=2.
巩固练习1 根据下列条件，分别判断以a，b，C为边的三角形能否构成直角三角形．
(1)a=1，b=,c=2；
(2)a=5，b=6，c=10；
(3)a：b：c=1：1：
典型例题2 已知：如图，在△ABC中，CD⊥AB于点D，AC=4，BC=3，BD=．(1)求CD的长；(2)求AD的长；(3)判断△ABC是否是直角三角形，并说明理由．
巩固练习2 如图，在△DEF中，已知DE=17cm，EF=30cm，EF边上的中线DG=8cm，试说△DEF是等腰三角形．
一、选择题
1．以下列各组数为边长，能构成直角三角形的是( )
A．5，7，8 B．1，2，3 C．，， D．，，2
2．三角形的三边长满足(a+b)2一c2=2ab，则此三角形是( )
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形
3．下列条件不能判定△ABC是直角三角形的是( )
A．∠A=∠C=45°
B．AC2+BC2=AB2
C．∠A：∠B：∠C=3：4：5
D．a：b：c=3：4：5
4．将直角三角形的三边长都扩大3倍后，得到的三角形是 ( )
A．钝角三角形 B．可能是锐角三角形
C．直角三角形 D．不能确定
二、填空题
5．一个三角形的三边长分别为6，8，10，则这个三角形最长边上的高为_______．
6．已知|x-9|+(y-12)2+=0，则以x，y，z为三条边的三角形是_______三角形．
7．下列结论：①在△ABC中，∠C=∠A一∠B，则△ABC为直角三角形；②在△ABC中，∠A：∠B：∠C=5 ：2：3，则△ABC为直角三角形；③在△ABC中，若a= c，b=c，则△ABC为直角三角形；④在△ABC中，若a：b：c=1：1：2，则△ABC为直角三角形，其中
正确的有____________．(填序号)
三、解答题
8．已知a，b，c为△ABC的三边长，且满足a2 c2-b2c2=a4-b4，请判断△ABC的形状，并说明理由．
9.如图，在四边形ABCD中，∠A=90°，AD=AB=4，BC=6，CD=2，求∠ADC的度数．
10．如图，∠A=∠D=90°，AB=CD=24，AD=BC=50，E是AD上一点，且AE：ED=9：16，试猜想∠BEC是锐角、钝角还是直角 请说明你的猜想．
2．6提高班习题精选
1．从长度为9，12，15，36，39的五根木棒中，选出三根首尾连接，能组成直角三角形的个数有 ( )
A．1个 B．2个 C．3个 D．4个
2．若△ABC的三边a，b，c满足(a一b)(a2+b2-c2)=0，则△ABC是 ( )
A．等腰三角形 B．直角三角形 C．等腰直角三角形
D．等腰三角形或直角三角形或等腰直角三角形
3．如图，矩形纸片ABCD中，AB=8cm，把矩形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若AF=cm，则AD的长为( )
A．4cm B．5cm C．6cm D．7cm
4．已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=3，则图中阴影部分的面积为________．
5．如图所示，在△ABC中，D为BC边上一点，若AB=13，BD=5，AD=12，BC=14，则AC=_____.
6．边长为4cm的正三角形的面积为_________．
7．如图，有一张直角三角形的纸片，两直角边分别为AB=6，BC=8，将直角边AB折叠，使它落在斜边AC上，折痕为AD，则BD=___________．
8．如图，在正方形ABCD中，E为BC的中点，F为CD的四等分点，连结AE，AF，EF，请说
明△AEF是直角三角形．
9．有一块菜地，地形如图所示，试求它的面积S．
10．若△ABC的三边a，b，C满足条件：a2+b2+c2+338=10a+24b+26c．试判断△ABC的形状，并说明理由．
11．如图所示，在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c，斜边上的高CD长为h．试说明：
12．如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BP=BQ，连结CQ．
(1)观察并猜想AP与CQ之间的大小关系，并说明理由．
(2)若PA=3，PB=4，PC=5，连结PQ，判断△PQC的形状并说明理由．
1．【2010·钦州】如图是一张直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为 ( )
A．4cm B．5cm C．6cm D．10cm
2．【2010·河池】如图是用4个全等的直角三角形与l个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边(x>y)，下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9．
其中说法正确的是 ( )
A．①② B．①②③ C．①②④ D．①②③④
参考答案
2.6 探索勾股定理(1)
【课前热身】
1．平方和 平方 a2+b2=c2 2．5 8 3． 4． 5.24
【课堂讲练】
典型例题l 解：(1)b= ==40(2)设a=8x, b=15x (8x)2+(15x)2=342，得x=2 ∴a=16
巩固练习l 解：(1)x= =15 (2)y= =8
典型例题2 解：∵△ADE为等腰直角三角形 DE= ∴AD==6m ∴AB=AD=6m ∵∠BAC=60°∴AC=AB=3m ∴BC==m
巩固练习2 解：∵S1=π(AC)2=AC2 S2=π（BC）2=BC2 S3=π（AB）2=AB2 又∵∠ACB=90° ∴AC2+BC2=AB2 ∴S1+S2=S3
【跟踪演练】
1．C 2．C 3．C 4．C 5．74 6．96 7．24 8．解：∵AB=AC，AD⊥BC ∴BD=BC=3 在Rt△ABD中,∵∠ADB=90°∴AD= ＝=4 9．解：在Rt△ABC中，∵∠C=90°∴AB= == 15 ∴旗杆的长=9+15=24(m) 10．解：(1)在Rt△AOB中，∵∠O=90°∴0B===7（m） (2) 在Rt△A′B′O中，∠O=90°
A′0=24—4=20 A′B′=25 ∴B′O==15 ∴BB′=B′0-BO=15—7=8(m)
即梯子底部在水平方向滑动了8m
2．6探索勾股定理(2)
【课前热身】
1．平方 直角三角形 直角 2．直角三角形 3．5、12、13 7、24、25等 4．30 5．直角三角形 斜
【课堂讲练】
典型例题l 解：(1) ∵ ∴能构成直角三角形 (2)a2+c2=1+4=5 b2=5 ∵a2+c2= b2 ∴能构成直角三角形
巩固练习l 能构成直角三角形 不能构成直角三角形 能构成直角三角形
典型例题2 解：(1) ∵CD⊥AB ∴∠CDB和∠CDA都是直角 在Rt△CDB中，CD2=CB2-BD2=32 -= ∴CD= (2)在Rt△ACD中 ∵AC=4，CD= ∴AD2=AC2-CD2=42- = ∴AD= (3) 在Rt△ABC中，∵AB= =5 AB2=25=AC2+BC2 ∴△ABC是直角三角形
巩固练习2 解：∵DG为EF中线 EF=30cm ∴EG=15cm ∵DE=17cm DG=8cm ∴DG2+EG2=DE2 ∴△DEG为直角三角形 ∴DG⊥EF 又∵G为EF中点 ∴△DEF是等腰三角形
【跟踪演练】
1．D 2．B 3.C 4．C 5．4.8 6．直角 7．①②③ 8．解：由a2 c2－b2c2=a4—b4得(a2—b2)c2=(a2+b2)(a2一b2) ∴a2一b2=0或a2+b2=c2 当a2一b2=0时得a=b ∴△ABC是等腰三角形当a 2+b2=c2时，时得△ABC是直角三角形 ∴△ABC为等腰三角形或直角三角形 9．解：连结DB ∵AD=AB=4 ∠A=90°∴△ADB是等腰直角三角形∠ADB=45°DB=在△BCD中，∵CD2+BD2＝32+4=36=BC2 ∴∠BDC=90°∴∠ADC=∠ADB+∠CDB=45°+90°=135° 10．解：∠BEC是直角，理由：∵AD=50，AE：ED=9：16 ∴AE=18 ED=32 ∵BE2=AB2+AE2 =900 CE2=DE2+CD2=1600 ∴BE2+CE2=2500=BC2 ∴∠BEC=90°
2．6提高班习题精选
【提高训练】
1．B 2．D 3.C 4． 5．15 6．cm 7．3 8．解：设正方形的边长为4a，则DF=3a，CF=a，EC=2a ∴AF=5a EF= AE= ∴AE2+EF2=AF2 ∴△AEF为直角三角形 9．解：连结BC，由∠CDB=90°，CD=3，DB=4，得BC=5，又∵AC=12 AB=13 ∴∠ACB=90°∴S=S△ACB—S△DCB=＝30－6=24 10．解：由题意得(a2-10a+25)+(b2-24b+144)+(c2-2bc+169)=0 得（a-5）2+(b-12)2+(c-13)2=0 得a=5 b=12 c=13 ∵a2+b2=c2 ∴△ABC是直角三角形 ll．证明：∵S△ABC = ∴ ∴ ∴结论成立 l2．解：(1)AP=CQ ,理由：∵△ABC为正三角形 ∴AB=BC ∠ABC=60° 又∵∠CBQ=60°∴∠ABC=∠PBQ，从而得∠ABP=∠CBQ 又∵BP=BQ ∴∠ABP≌∠BQC ∴AP=CQ (2) △PQC是直角三角形，理由：连结PQ，易证△BPQ为等边三角形 ∴PQ=BP ∵PA=3，PB=4，PC=5 ∴PQ2+QC2=PC2 ∴△PQC为Rt△
【中考链接】
1． B 2．B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 （共 9 页） 版权所有@21世纪教育网