名师导学——2.7 直角三角形全等的判定
文档属性
| 名称 | 名师导学——2.7 直角三角形全等的判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 364.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-16 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
2.7直角三角形全等的判定
课前热身
1.__________和一条________对应相等的两个直角三角形全等,简写成“斜边、直角边”或“_________”.
2.角的内部,到角的两边距离相等的点,在_____________________________.
3.判定两个直角三角形全等共有五种方法,分别是SSS,_______,_______,_______,________.
4.如图,∠A=∠B=90°,请你再添加一个条件,使△ACD≌△BDC,并在后面的括号里写出判定全等的依据:①_______________( );②______________( );③_______________( ).
5.如图,在△ABC中,∠C=90°,AD平分∠CAB,CD=5cm,那么点D到AB的 距 离是___________.
典型例题1 如图,△ABC和△DBC 都是直角三角形,∠A=∠D=90°,AB=CD,请说明:△EBC是等腰三角形.
巩固练习1 如图,已知AB=CD,DE⊥AC,BF⊥AC,E,F为垂足,DE=BF,问:AB与CD平行吗 请说明理由.
典型例题2 如图,在△ABC中,∠ABC的平分线和∠ACB的平分线相交于点P,则AP平分∠BAC,请说明理由.
巩固练习2 已知:如图,在△ABC中,D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且BF=CE,则点D在∠BAC的平分线上,请说明理由.
一、选择题
1.如图,在△ABC中,AD⊥BC,D为BC的中点,则△ABD≌△ACD,其依据是 ( )
A.ASA B.HL C.SAS D.AAS
2.如图所示,∠ACB=∠BDE=90°,AC=DE,则下列条件中,不能使△ABC≌△EBD成立的是( )
A.∠A=∠E B.BC=BD C.AB=BD D.∠ABE=∠CBD
3.下列条件中,不能用来说明Rt△ABC≌Rt△A′B′C′(其中∠C=∠C′=90°)的是 ( )
A.∠A=∠A′,AC=A′C′ B.AC=B′C′,BC=A′C′
C.∠B=∠B ′,AB=A ′B′ D.∠B=∠B ′,AC=B ′C ′
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC=10cm,那么AE+DE= ( )
A.9cm B.10cm C.11cm D.12cm
二、埴空颗
5.如图,AB=CD,BF=DE,AE⊥BD,CF⊥BD,则图中能用“HL”定理判定全等的三角形是_________________.
6.如图,已知BD⊥AE于点B,C是BD上的点,且BC=BE,要使Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D,或____________,或_____________,或____________.
7.如图,AD平分∠CAB,DC⊥AC,DB⊥AB,且DC=DB,若∠1=30°,则∠CAB的度数是_____.
三、解答题
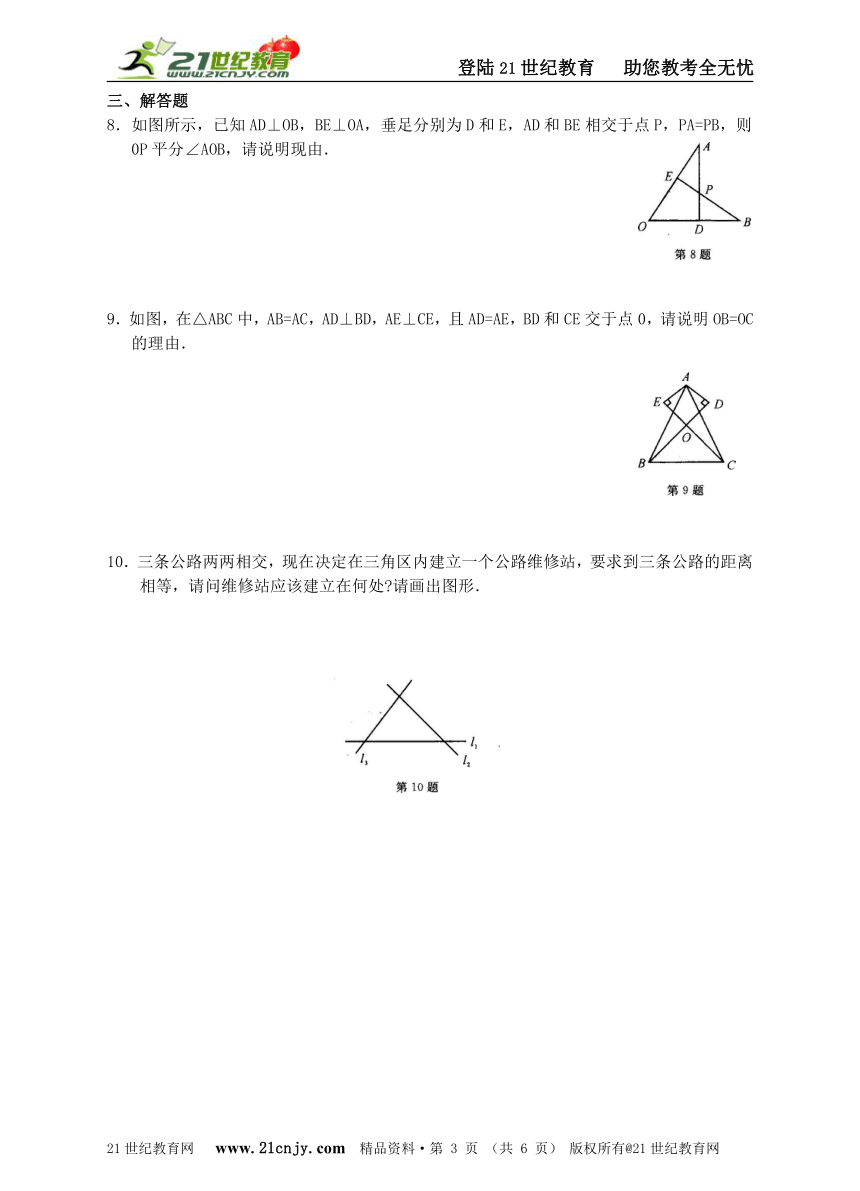
8.如图所示,已知AD⊥OB,BE⊥OA,垂足分别为D和E,AD和BE相交于点P,PA=PB,则0P平分∠AOB,请说明现由.
9.如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点0,请说明OB=OC的理由.
10.三条公路两两相交,现在决定在三角区内建立一个公路维修站,要求到三条公路的距离相等,请问维修站应该建立在何处 请画出图形.
2.7提高班习题精选
1.如图,把Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是 ( )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
2.如图,在R△ABC中,∠C=90°,AD是∠BAC的平分线,如果BC=32cm,BD:CD=9:7,那么点D到AB的距离是 ( )
A.12cm B.14cm C.16cm D.18cm
3.如图,AB=AC,DE⊥AB,DF⊥AC,AD⊥BC,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
4.如图,0M平分∠POQ,MP⊥0P,MQ⊥OQ,垂足分别为P,Q,且S△OPM=6cm2,OP=2cm,则MQ=_____.
5.如图所示,已知AB⊥AC,AC⊥CD,且AB=CD,则图中共有_________对全等三角形.
6.如图,在△ABC中,AB=AC,D为 BC上一点,连结AD,点E在AD上,过点E作EM⊥AB,EN⊥AC,垂足分别为M,N;那∠下面4个结论中:①如果AD⊥BC,那∠EM=EN;②如果EM=EN,那么∠l=∠2;③如果EM=EN,那∠AM=AN;④如果EM=EN,那么∠3=∠4.其中正确的有____________.(填序号)
7.已知:如图,在△ABC中,AD⊥BC,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,求:∠AEB的度数.
8.如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线,则AC+CD=AB,请说明理由.
9.已知:如图,AC⊥AB于A,BD⊥AB于B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
10.如图,在△ABC中,AB=7,BC=24,AC=25,(1)在△ABC内是否存在一点P到各边的距离相等,如果存在,请作出这一点,并说明理由.(2)求出这个距离.
11.已知:如图,点0到△ABC的两边AB,AC,所在直线的距离相等,且OB=OC.
(1)如图(1),若点0在边BC上,请说明AB=AC的理由;
(2)如图(2),若点O在△ABC的内部,请说明AB=AC的理由;
(3)若点0在△ABC的外部,AB=AC成立吗 请说明理由.
1.【2010·益阳】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是 ( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
2.【2009·怀化】如图,P是△BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:(1)PE=PF;(2)点P在∠BAC的角平分线上.
参考答案
2.7直角三角形全等的判定
【课前热身】
1.斜边 直角边 HL 2.这个角的平分线上 3.SAS ASA AAS HL 4.AC=BD HL AD=BC HL ∠ACD=∠BDC AAS 5.5cm
【课堂讲练】
典型例题l 解:∵∠A=∠D,AB=DC,BC=BC ∴Rt△ABC≌Rt△DCB(HL) ∴∠ACB=∠DBC ∴△ECB是等腰三角形(有两个角相等的三角形是等腰三角形)
巩固练习l 解:AB∥CD,理由:∵DE⊥AC,BF⊥AC ∴△CDE和△AFB是Rt△ ∵AB=CD,DE=BF ∴Rt△CDE≌Rt△ABF(HL) ∴∠C=∠A ∴AB∥CD
典型例题2 解:作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于F. ∵BP平分∠ABC ∴PD=PE
同理,PE=PF ∴PD=PF ∴AP平分∠BAC
巩固练习2 解:∵DF⊥AB,DE⊥AC ∴△DBF和△DCE都是直角三角形 ∵D是BC的中点 ∴DB=DC 又∵BF=CE ∴Rt△DBF≌Rt△DCE(HL) ∴DF=DE ∴点D在∠BAC的平分线上
(到一个角两边距离相等的点,在这个角的平分线上)
【跟踪演练】
1.C 2.C 3.D 4.B 5.Rt△ABE≌Rt△CDF 6.AC=DE ∠ACB=∠E AB=DB 7.60° 8.解:由AD⊥OB,BE⊥OA,得∠AEP=∠BDP=90° 又∠APE=∠DPB,PA=PB ∴△APE≌△BPD(AAS) ∴PE=PD ∴0P平分∠AOB(到一个角两边距离相等的点,在这个角的平分线上) 9.解:∵AD⊥BD,AE⊥CE ∴∠E=∠D=90° AE=AD AB=AC ∴△AEC≌△ABD ∴∠ABD=∠ACE ∵AB=AC ∴∠ABC=∠ACB ∴∠OBC=∠OCB ∴OB=OC 10.解:作三个角的角平分线角平分线的交点即所求位置
2.7提高班习题精选
【提高训练】
1.D 2.B 3.C 4.6cm 5.4 6.①②③④ 7.解:由AD⊥BC,BF=AC,FD=CD,可得Rt△BDF≌Rt△ACD(HL) ∴∠FBD=∠CAD ∴∠AEB=∠FBD+∠C=∠CAD+∠C=90°8.解:过D作DE⊥AB于点E 由∠C=90°,AC=BC,知∠B=90° 又∵DE⊥AB ∴△BED是等腰Rt,BE=DE ∵AD是∠A的平分线 ∴DE=CD AE=AC ∴AC+CD=AE+BE=AB 9.解:∵AC⊥AB,BD⊥AB ∴△ACE和△BDE都是Rt△ ∵CE=DE,AC=BE ∴Rt△ACE≌Rt△BDE(HL) ∴∠C=∠DEB ∴∠CED=180°-∠AEC-∠DEB=180°-∠AEC-∠C=90°∴CE⊥ED 10.解:(1)存在,作内角的角平分线,它们的交点即为点P (2) ∵AB2+BC2=AC2 ∴∠B=90° 设这个距离为d,则S△ABC=S△APC+S△BPC+S△ABP ∴=++ ∴d=3 11.解:(1)过点0分别作OE⊥AB,OF⊥AC,垂足分别为E、F,由题意可知0E=OF,OB=OC ∴Rt△OEB≌Rt△OFC(HL) ∴∠B=∠C ∴AB=AC (2)过点0分别作0E⊥AB,OF⊥AC, E,F为垂足,则易证Rt △OEB≌Rt △OFC ∴∠0BE=∠OCF,又OB=OC ∴∠0BC=∠OCB ∴∠ABC=∠ACB ∴AB=AC (3)不一定成立,只有当∠A的平分线所在直线与边BC垂直平分线重合时,才有AB=AC,否则,AB ≠AC.
【中考链接】
1.B 2.证明: (1)连结AP.∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°.又AE=AF,AP=AP,∴Rt△AEP≌Rt△AFP.∴PE=PF.(2) ∵PE=PF,PE⊥AB,PF⊥AC,∴P在∠BAC的角平分线上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 6 页 (共 6 页) 版权所有@21世纪教育网
2.7直角三角形全等的判定
课前热身
1.__________和一条________对应相等的两个直角三角形全等,简写成“斜边、直角边”或“_________”.
2.角的内部,到角的两边距离相等的点,在_____________________________.
3.判定两个直角三角形全等共有五种方法,分别是SSS,_______,_______,_______,________.
4.如图,∠A=∠B=90°,请你再添加一个条件,使△ACD≌△BDC,并在后面的括号里写出判定全等的依据:①_______________( );②______________( );③_______________( ).
5.如图,在△ABC中,∠C=90°,AD平分∠CAB,CD=5cm,那么点D到AB的 距 离是___________.
典型例题1 如图,△ABC和△DBC 都是直角三角形,∠A=∠D=90°,AB=CD,请说明:△EBC是等腰三角形.
巩固练习1 如图,已知AB=CD,DE⊥AC,BF⊥AC,E,F为垂足,DE=BF,问:AB与CD平行吗 请说明理由.
典型例题2 如图,在△ABC中,∠ABC的平分线和∠ACB的平分线相交于点P,则AP平分∠BAC,请说明理由.
巩固练习2 已知:如图,在△ABC中,D是BC的中点,DF⊥AB于点F,DE⊥AC于点E,且BF=CE,则点D在∠BAC的平分线上,请说明理由.
一、选择题
1.如图,在△ABC中,AD⊥BC,D为BC的中点,则△ABD≌△ACD,其依据是 ( )
A.ASA B.HL C.SAS D.AAS
2.如图所示,∠ACB=∠BDE=90°,AC=DE,则下列条件中,不能使△ABC≌△EBD成立的是( )
A.∠A=∠E B.BC=BD C.AB=BD D.∠ABE=∠CBD
3.下列条件中,不能用来说明Rt△ABC≌Rt△A′B′C′(其中∠C=∠C′=90°)的是 ( )
A.∠A=∠A′,AC=A′C′ B.AC=B′C′,BC=A′C′
C.∠B=∠B ′,AB=A ′B′ D.∠B=∠B ′,AC=B ′C ′
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC=10cm,那么AE+DE= ( )
A.9cm B.10cm C.11cm D.12cm
二、埴空颗
5.如图,AB=CD,BF=DE,AE⊥BD,CF⊥BD,则图中能用“HL”定理判定全等的三角形是_________________.
6.如图,已知BD⊥AE于点B,C是BD上的点,且BC=BE,要使Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D,或____________,或_____________,或____________.
7.如图,AD平分∠CAB,DC⊥AC,DB⊥AB,且DC=DB,若∠1=30°,则∠CAB的度数是_____.
三、解答题
8.如图所示,已知AD⊥OB,BE⊥OA,垂足分别为D和E,AD和BE相交于点P,PA=PB,则0P平分∠AOB,请说明现由.
9.如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点0,请说明OB=OC的理由.
10.三条公路两两相交,现在决定在三角区内建立一个公路维修站,要求到三条公路的距离相等,请问维修站应该建立在何处 请画出图形.
2.7提高班习题精选
1.如图,把Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是 ( )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
2.如图,在R△ABC中,∠C=90°,AD是∠BAC的平分线,如果BC=32cm,BD:CD=9:7,那么点D到AB的距离是 ( )
A.12cm B.14cm C.16cm D.18cm
3.如图,AB=AC,DE⊥AB,DF⊥AC,AD⊥BC,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
4.如图,0M平分∠POQ,MP⊥0P,MQ⊥OQ,垂足分别为P,Q,且S△OPM=6cm2,OP=2cm,则MQ=_____.
5.如图所示,已知AB⊥AC,AC⊥CD,且AB=CD,则图中共有_________对全等三角形.
6.如图,在△ABC中,AB=AC,D为 BC上一点,连结AD,点E在AD上,过点E作EM⊥AB,EN⊥AC,垂足分别为M,N;那∠下面4个结论中:①如果AD⊥BC,那∠EM=EN;②如果EM=EN,那么∠l=∠2;③如果EM=EN,那∠AM=AN;④如果EM=EN,那么∠3=∠4.其中正确的有____________.(填序号)
7.已知:如图,在△ABC中,AD⊥BC,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,求:∠AEB的度数.
8.如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线,则AC+CD=AB,请说明理由.
9.已知:如图,AC⊥AB于A,BD⊥AB于B,E为线段AB上一点,且有AC=BE,CE=DE,试说明CE⊥ED.
10.如图,在△ABC中,AB=7,BC=24,AC=25,(1)在△ABC内是否存在一点P到各边的距离相等,如果存在,请作出这一点,并说明理由.(2)求出这个距离.
11.已知:如图,点0到△ABC的两边AB,AC,所在直线的距离相等,且OB=OC.
(1)如图(1),若点0在边BC上,请说明AB=AC的理由;
(2)如图(2),若点O在△ABC的内部,请说明AB=AC的理由;
(3)若点0在△ABC的外部,AB=AC成立吗 请说明理由.
1.【2010·益阳】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是 ( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
2.【2009·怀化】如图,P是△BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:(1)PE=PF;(2)点P在∠BAC的角平分线上.
参考答案
2.7直角三角形全等的判定
【课前热身】
1.斜边 直角边 HL 2.这个角的平分线上 3.SAS ASA AAS HL 4.AC=BD HL AD=BC HL ∠ACD=∠BDC AAS 5.5cm
【课堂讲练】
典型例题l 解:∵∠A=∠D,AB=DC,BC=BC ∴Rt△ABC≌Rt△DCB(HL) ∴∠ACB=∠DBC ∴△ECB是等腰三角形(有两个角相等的三角形是等腰三角形)
巩固练习l 解:AB∥CD,理由:∵DE⊥AC,BF⊥AC ∴△CDE和△AFB是Rt△ ∵AB=CD,DE=BF ∴Rt△CDE≌Rt△ABF(HL) ∴∠C=∠A ∴AB∥CD
典型例题2 解:作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于F. ∵BP平分∠ABC ∴PD=PE
同理,PE=PF ∴PD=PF ∴AP平分∠BAC
巩固练习2 解:∵DF⊥AB,DE⊥AC ∴△DBF和△DCE都是直角三角形 ∵D是BC的中点 ∴DB=DC 又∵BF=CE ∴Rt△DBF≌Rt△DCE(HL) ∴DF=DE ∴点D在∠BAC的平分线上
(到一个角两边距离相等的点,在这个角的平分线上)
【跟踪演练】
1.C 2.C 3.D 4.B 5.Rt△ABE≌Rt△CDF 6.AC=DE ∠ACB=∠E AB=DB 7.60° 8.解:由AD⊥OB,BE⊥OA,得∠AEP=∠BDP=90° 又∠APE=∠DPB,PA=PB ∴△APE≌△BPD(AAS) ∴PE=PD ∴0P平分∠AOB(到一个角两边距离相等的点,在这个角的平分线上) 9.解:∵AD⊥BD,AE⊥CE ∴∠E=∠D=90° AE=AD AB=AC ∴△AEC≌△ABD ∴∠ABD=∠ACE ∵AB=AC ∴∠ABC=∠ACB ∴∠OBC=∠OCB ∴OB=OC 10.解:作三个角的角平分线角平分线的交点即所求位置
2.7提高班习题精选
【提高训练】
1.D 2.B 3.C 4.6cm 5.4 6.①②③④ 7.解:由AD⊥BC,BF=AC,FD=CD,可得Rt△BDF≌Rt△ACD(HL) ∴∠FBD=∠CAD ∴∠AEB=∠FBD+∠C=∠CAD+∠C=90°8.解:过D作DE⊥AB于点E 由∠C=90°,AC=BC,知∠B=90° 又∵DE⊥AB ∴△BED是等腰Rt,BE=DE ∵AD是∠A的平分线 ∴DE=CD AE=AC ∴AC+CD=AE+BE=AB 9.解:∵AC⊥AB,BD⊥AB ∴△ACE和△BDE都是Rt△ ∵CE=DE,AC=BE ∴Rt△ACE≌Rt△BDE(HL) ∴∠C=∠DEB ∴∠CED=180°-∠AEC-∠DEB=180°-∠AEC-∠C=90°∴CE⊥ED 10.解:(1)存在,作内角的角平分线,它们的交点即为点P (2) ∵AB2+BC2=AC2 ∴∠B=90° 设这个距离为d,则S△ABC=S△APC+S△BPC+S△ABP ∴=++ ∴d=3 11.解:(1)过点0分别作OE⊥AB,OF⊥AC,垂足分别为E、F,由题意可知0E=OF,OB=OC ∴Rt△OEB≌Rt△OFC(HL) ∴∠B=∠C ∴AB=AC (2)过点0分别作0E⊥AB,OF⊥AC, E,F为垂足,则易证Rt △OEB≌Rt △OFC ∴∠0BE=∠OCF,又OB=OC ∴∠0BC=∠OCB ∴∠ABC=∠ACB ∴AB=AC (3)不一定成立,只有当∠A的平分线所在直线与边BC垂直平分线重合时,才有AB=AC,否则,AB ≠AC.
【中考链接】
1.B 2.证明: (1)连结AP.∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°.又AE=AF,AP=AP,∴Rt△AEP≌Rt△AFP.∴PE=PF.(2) ∵PE=PF,PE⊥AB,PF⊥AC,∴P在∠BAC的角平分线上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 6 页 (共 6 页) 版权所有@21世纪教育网
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
