第四章 相似三角形章末检测题(基础篇含解析)
文档属性
| 名称 | 第四章 相似三角形章末检测题(基础篇含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 16:23:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版九年级上册第四章 相似三角形 章末检测(基础篇)
一、单选题
1.已知点C是线段 的黄金分割点(其中 ), .则线段 的大小是(? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.若3x=2y(xy≠0),则下列比例式成立的是(? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,已知一组平行线a//b//c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=3,DE=1.6,则EF=(??? )
A.?2.4????????????????????????????????????????B.?1.8????????????????????????????????????????C.?2.6????????????????????????????????????????D.?2.8
4.如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
5.下列每组的两个图形中,不是位似图形的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
6.下列四条线段能成比例线段的是(? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
7.如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是(?? )
A.?BC∶DE=1∶2?????????????????????????????????????????????????????B.?△ABC的面积∶△DEF的面积=1∶2
C.?∠A的度数∶∠D的度数=1∶2???????????????????????????D.?△ABC的周长∶△DEF的周长=1∶2
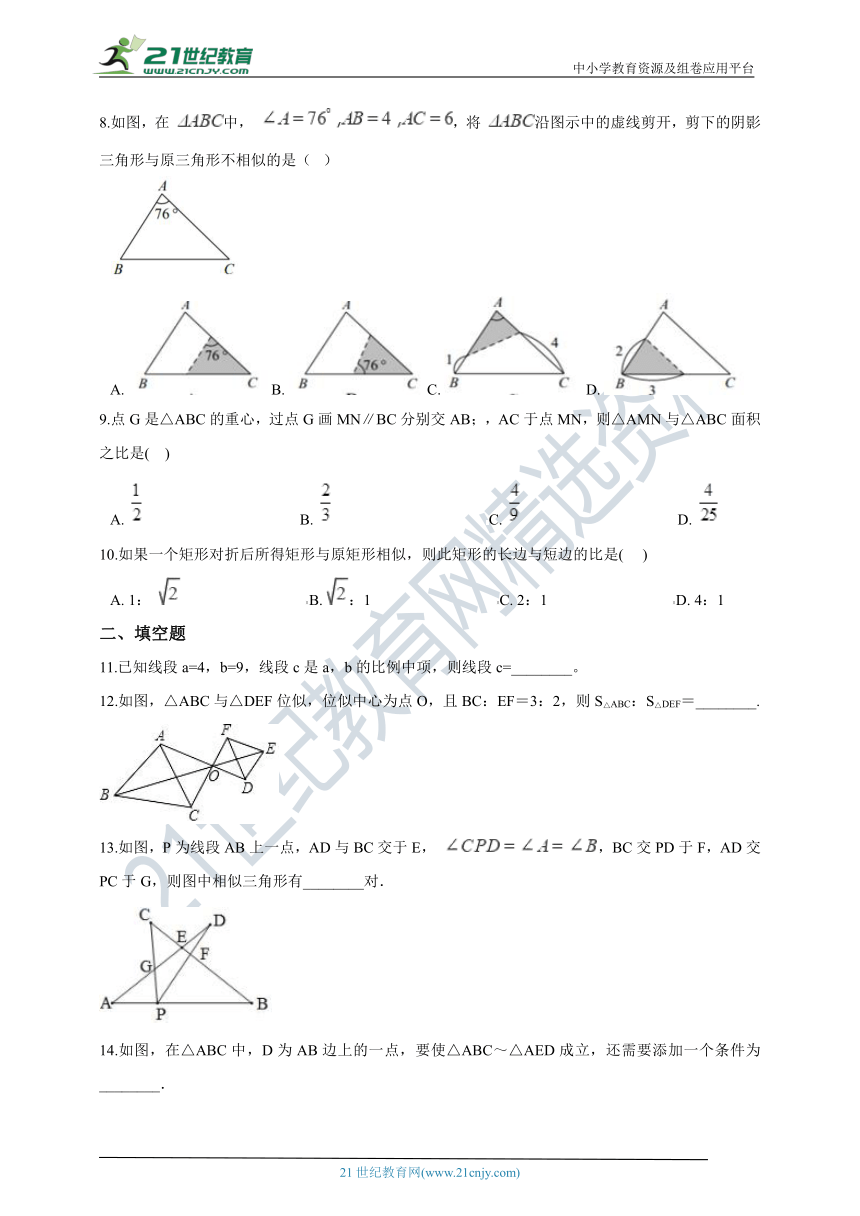
8.如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(? )
A.??B.?C.???D.?
9.点G是△ABC的重心,过点G画MN∥BC分别交AB;,AC于点MN,则△AMN与△ABC面积之比是(?? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
10.如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是(??? )
A.?1: ?????????????????????????????????B.?:1?????????????????????????????????C.?2:1?????????????????????????????????D.?4:1
二、填空题
11.已知线段a=4,b=9,线段c是a,b的比例中项,则线段c=________。
12.如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=________.
13.如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有________对.
14.如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为________.
15.在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是________km.
16.如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于________.
三、解答题
17.已知线段a、b、c,且 .
(1)求 的值;
(2)若线段a、b、c满足 ,求a、b、c的值.
18.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,求 的值.
19.如图,在等腰△ABC巾,AD是顶角∠BAC的角平分线,BE是腰AC边上的高,垂足为点E,求证:△ACD∽△BCE.
20.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
21.在方格纸中,我们把像△ABC这样的顶点在小正方形的顶点的三角形叫做格点三角形.如图,左边的5×5的方格中有一个△ABC.
(1)在右边三个5×5的方格纸中各画出一个与△ABC相似且互不全等的格点三角形
(2)直接写出在一个6×6的方格纸中,可以画出的与△ABC相似的且互不全等的所有格点三角形的个数(不包括与△ABC全等的三角形)
22.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)①请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
②以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2;
(2)填空:△AA1A2的面积为________.
23.如图,矩形 中, , ,点 在 上,连接 点 在直线 上, 交 于点 .
(1)求证: 是等腰三角形;
(2)求证: ;
(3)当 为 中点时,求 的长.
24.淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
(2)如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
答案解析部分
一、单选题
1. D
考点:黄金分割
解:∵C是线段 的黄金分割点,
∴ ,
∴ ,
故答案为:D.
分析:根据黄金比值 计算即可.
2. D
考点:比例的性质
解:A、∵,
∴3y=2x,故A不符合题意;
B、∵,
∴xy=6,故B不符合题意;
A、∵,
∴3y=2x,故C不符合题意;
A、∵,
∴3x=2y,故D符合题意;
故答案为:D
分析:利用比例的性质:两内项之积等于两外项之积,再对各选项逐一判断,可得比例式正确的选项。
3. A
考点:平行线分线段成比例
解:∵a∥b∥c,
∴ ,
即 ,
∴EF=2.4.
故答案为:A.
分析:根据平行线分线段成比例定理得到 ,然后利用比例性质可求出EF的长.
4. A
考点:相似三角形的判定与性质
解:∵ ,
∴AC=1.2m+12.8m=14m
∵标杆 和建筑物CD均垂直于地面
∴BE//CD
∴△ABE∽△ACD
∴ ,即 ,解得CD=17.5m.
故答案为:A.
分析:先求得AC,再说明△ABE∽△ACD,最后根据相似三角形的性质列方程解答即可.
5. B
考点:位似变换
解:对应顶点的连线相交于一点的两个相似多边形叫位似图形.
据此可得A、C、D三个图形中的两个图形都是位似图形;
而B的对应顶点的连线不能相交于一点,故不是位似图形.
故答案为:B.
分析:如果两个多边形不仅相似,而且对应点的连线所在的直线相交于一点,对应边互相平行(或在一条直线上),像这样的两个图形叫做位似图形,据此判断即可.
6. C
考点:比例线段
解: 所以A不是成比例线段,
?所以B不是成比例线段,
?所以C是成比例线段,
?所以D不是成比例线段.
故答案为:C.
分析:先把四条线段按从小到大的顺序排列,若a,b,c,d成比例,即有a:b=c:d.只要代入验证即可.
7. D
考点:相似三角形的性质
解:相似三角形的性质:相似三角形的周长比会等于相似比.
D一定成立.
都不一定成立.
故选D.
分析:根据相似三角形的性质“①相似三角形的对应角相等.②相似三角形的对应边成比例.③相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比.④相似三角形的周长比等于相似比.⑤相似三角形的面积比等于相似比的平方.”可判断求解.
8. D
考点:相似三角形的判定
解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形对应边成比例 且夹角相等,故两三角形相似,故本选项不符合题意.
D、两三角形中,有 但夹角不一定相等,故不能判定两三角形相似,故本选项符合题意;
故答案为:D
分析:根据相似三角形的判定定理对各选项进行逐一判定即可.
9. C
考点:相似三角形的判定与性质
解:∵MN∥BC,
∴△AMN∽△ABC,
又∵点G为 △ABC的重心,
,
∴.
故答案为:C.
分析:根据相似三角形的判定可得△AMN∽△ABC,再由△ABC的重心得 , 根据相似三角形的性质:相似三角形的面积比等于相似比的平方,由此即可得出答案.
10. B
考点:相似多边形的性质
解:如图,
设AB=a, BC=b,
∵矩形ABCD∽矩形BEFA,
∴AB:BC=AF:AB,
∴a:b=b:a,
∴a2=b2,
∴b:a=:1,
故答案为:B.
分析:设短边AB=a, 长边BC=b, 由相似多边形的性质列式即可求出矩形的长边与短边的比值.
二、填空题
11. 6
考点:比例线段
解:根据比例中项的概念结合比例的基本性质,得c2=4×9,解得c=±6(线段是正数,负值舍去),
∴c=6cm,
故答案为:6.
分析:根据比例中项的定义,列出比例式即可得出c.
12. 9:4
考点:相似三角形的性质
解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,
∵BC:EF=3:2,
∴ ,
故答案为:9:4.
分析:先根据位似图形的概念得到△ABC∽△DEF,根据相似三角形的性质计算即可得到答案.
13. 3
考点:相似三角形的判定
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C
∴∠APG=∠BFP,
∴△APG∽△BFP
则图中相似三角形有3对
分析:先根据条件证明△PCF∽△BCP,利用相似三角形的性质:对应角相等,再证明△APD∽△PGD,进而证明△APG∽△BFP再证明时注意图形中隐含的相等的角.
14. ∠B=∠AED或∠C=∠ADE或
考点:相似三角形的判定
解:本题答案不唯一,
∵在△AED和△ABC中,∠A=∠A,
∴(1)当添加条件:∠B=∠AED时,△ABC∽△AED;(2)当添加条件:∠C=∠ADE时,△ABC∽△AED;(3)当添加条件: 时,△ABC∽△AED.
故答案为:∠B=∠AED?? 或∠C=∠ADE? 或 .
分析:根据相似三角形的判定定理,添加合适的条件即可。
15. 160
考点:相似多边形的性质
解:∵周长之比等于相似比,
∴这个地区的实际周长是320×50000=16000000cm=160km;
故答案为160.
分析:地图与实际的多边形按照比例放大与缩小,根据相似多边形的相似比求解即可
16.
考点:勾股定理,相似三角形的判定与性质
解:∵ ,
,
,
∴ ,
∴△ABC∽△DEF,
∴ ,
故答案为: .
分析:先证明两个三角形相似,再根据相似三角形的周长比等于相似比,得出周长比的值便可.
三、解答题
17. (1)解:设
则 , ,
∴
(2)解:∵
∴
解得
∴ , ,
考点:代数式求值,比例的性质
分析:(1)设 ,则 , , ,代入即可化简;(2)根据 得到 ,解出k即可求解.
18. 解:∵四边形ABCD是菱形,
∴BC∥AD
∴ =
∵CD∥AB
∴ =
∴ = =1
又∵AB=AD=1,
∴
=1.
答: 的值为1.
考点:菱形的性质,平行线分线段成比例
分析:根据四边形ABCD是菱形得到BC∥AD,从而得到 , , ,代入菱形的边长为1即可求得结论.
19. 证明:∵在等腰 中, 是顶角 的平分线,
∴ ⊥ ,
∴ ,
∵ 是腰 边上的高,垂足为 ,
∴ ,
∴ ,
又∵ ,
∴ ∽
考点:相似三角形的判定
分析:利用等腰三角形三线合一的性质,可证得∠ADC=90°,再利用三角形高的定义证明∠ADC=∠BEC,再利用有两组角对应相等的两三角形相似,可证得结论。
20.证明:∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=∠BAC=45°.
又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,
即四边形AFGE为正方形.
∴ = = = ,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似
考点:相似多边形的性质
分析:由正方形的性质可知;AC平分∠DAB,然后由角平分线的性质可知GE=GF,从而可证明四边形EGFA为正方形,故此四边形AFGE与四边形ABCD相似.本题主要考查的是相似多边形的判定、正方形的判定、角平分线的性质,证得四边形EAFG为正方形是解题的关键.
21. (1)解:如图,
(2)解:符合题意的三角形边长共有6个:①, 2,;②2,2, 2;③, , 5;④, 2, 5;⑤3,3, 3;⑥2, 4,2;
考点:相似三角形的判定
分析:(1)根据各点三角形的定义及相似三角形的判定方法即可得出答案;
(2)根据相似三角形的判定方法及格点三角形的定义即可得出符合题意的图形.
22. (1)解:如图所示,△A1B1C1、△A2B2C2即为所求;
(2)3
考点:作图﹣平移,作图﹣位似变换
解:(2)△AA1A2的面积为 ×6×1=3.
故答案为:3.
分析:(1)分别作出平移后对应点,再首尾顺次连接即可得;根据位似变换的概念作出变换后的对应点,再首尾顺次连接即可得;(2)利用三角形的面积公式计算可得.
23. (1)证明:∵四边形 是矩形,
∴ ,
∴ ,又 ,
∴ ,
∴ ,即 是等腰三角形;
(2)证明:作 于 ,
∵ , ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴
∴
(3)解:∵ 为 中点,
∴ ,
由(2)得, ,
∵ ,
∴ ,
∴ ,
设 ,则 ,
∵ ,
∴ ,即 ,
解得, ,即 ,
∴ ,
∴ .
考点:等腰三角形的判定,相似三角形的判定
分析:(1)由矩形的性质得出AD∥BC,由平行线的性质得出∠NAM=∠BMA,由已知∠AMN=∠AMB,得出∠AMN=∠NAM,即可得出结论;(2)由矩形的性质得出AD∥BC,AD=BC=2,AB=CD=3,由平行线的性质得出∠NAM=∠BMA,作NH⊥AM于H,由等腰三角形的性质得出AH= AM,证明△NAH∽△AMB,得出 ,即可得出结论;(3)求出BM=CM= BC= ×2=1,由(2)得AM2=2BM?AN,得出AM2=2AN,由勾股定理得出AM2=AB2+BM2=10,求出AN=5,得出DN=AN-AD=3,设DE=x,则CE=3-x,证明△DNE∽△CME,得出 ,求出DE= ,得出CE=DC-DE= ,再由勾股定理即可得出答案.
24. (1)解:由题意可知:AB=1.54-0.04=1.5m;BC=0.5m;CD=4m
∵ΔABC∽ΔEDC
∴ 即
∴
答:DE的长为12米.
(2)解:延长AD交BC的延长线于点F,过点D作DE⊥BC于点E
∵CD= m,∠DCE=45°
∴DE=CE=2m
∵
∵ 同一时刻物高与影长成正比
∴EF=2DE=4m
∴BF=EF+CE+BC=16m
∴AB= FB=8m
答:旗杆的高度约为8米.
考点:相似三角形的应用
分析:(1)根据题意得出△ABC∽△EDC,进而利用相似三角形的性质得出答案.(2)延长AD交BC的延长线于点F,过点D作DE⊥BC于点E,根据勾股定理求出ED的长,再由同一时刻物高与影长成正比得出EF的长,根据DE∥AB可知△EDF∽△ABF,由相似三角形的对应边成比例即可得出AB的长.
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版九年级上册第四章 相似三角形 章末检测(基础篇)
一、单选题
1.已知点C是线段 的黄金分割点(其中 ), .则线段 的大小是(? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.若3x=2y(xy≠0),则下列比例式成立的是(? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,已知一组平行线a//b//c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=3,DE=1.6,则EF=(??? )
A.?2.4????????????????????????????????????????B.?1.8????????????????????????????????????????C.?2.6????????????????????????????????????????D.?2.8
4.如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
5.下列每组的两个图形中,不是位似图形的是(?? )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
6.下列四条线段能成比例线段的是(? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
7.如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是(?? )
A.?BC∶DE=1∶2?????????????????????????????????????????????????????B.?△ABC的面积∶△DEF的面积=1∶2
C.?∠A的度数∶∠D的度数=1∶2???????????????????????????D.?△ABC的周长∶△DEF的周长=1∶2
8.如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(? )
A.??B.?C.???D.?
9.点G是△ABC的重心,过点G画MN∥BC分别交AB;,AC于点MN,则△AMN与△ABC面积之比是(?? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
10.如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是(??? )
A.?1: ?????????????????????????????????B.?:1?????????????????????????????????C.?2:1?????????????????????????????????D.?4:1
二、填空题
11.已知线段a=4,b=9,线段c是a,b的比例中项,则线段c=________。
12.如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=________.
13.如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有________对.
14.如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为________.
15.在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是________km.
16.如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于________.
三、解答题
17.已知线段a、b、c,且 .
(1)求 的值;
(2)若线段a、b、c满足 ,求a、b、c的值.
18.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,求 的值.
19.如图,在等腰△ABC巾,AD是顶角∠BAC的角平分线,BE是腰AC边上的高,垂足为点E,求证:△ACD∽△BCE.
20.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
21.在方格纸中,我们把像△ABC这样的顶点在小正方形的顶点的三角形叫做格点三角形.如图,左边的5×5的方格中有一个△ABC.
(1)在右边三个5×5的方格纸中各画出一个与△ABC相似且互不全等的格点三角形
(2)直接写出在一个6×6的方格纸中,可以画出的与△ABC相似的且互不全等的所有格点三角形的个数(不包括与△ABC全等的三角形)
22.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)①请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
②以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2;
(2)填空:△AA1A2的面积为________.
23.如图,矩形 中, , ,点 在 上,连接 点 在直线 上, 交 于点 .
(1)求证: 是等腰三角形;
(2)求证: ;
(3)当 为 中点时,求 的长.
24.淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
(2)如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
答案解析部分
一、单选题
1. D
考点:黄金分割
解:∵C是线段 的黄金分割点,
∴ ,
∴ ,
故答案为:D.
分析:根据黄金比值 计算即可.
2. D
考点:比例的性质
解:A、∵,
∴3y=2x,故A不符合题意;
B、∵,
∴xy=6,故B不符合题意;
A、∵,
∴3y=2x,故C不符合题意;
A、∵,
∴3x=2y,故D符合题意;
故答案为:D
分析:利用比例的性质:两内项之积等于两外项之积,再对各选项逐一判断,可得比例式正确的选项。
3. A
考点:平行线分线段成比例
解:∵a∥b∥c,
∴ ,
即 ,
∴EF=2.4.
故答案为:A.
分析:根据平行线分线段成比例定理得到 ,然后利用比例性质可求出EF的长.
4. A
考点:相似三角形的判定与性质
解:∵ ,
∴AC=1.2m+12.8m=14m
∵标杆 和建筑物CD均垂直于地面
∴BE//CD
∴△ABE∽△ACD
∴ ,即 ,解得CD=17.5m.
故答案为:A.
分析:先求得AC,再说明△ABE∽△ACD,最后根据相似三角形的性质列方程解答即可.
5. B
考点:位似变换
解:对应顶点的连线相交于一点的两个相似多边形叫位似图形.
据此可得A、C、D三个图形中的两个图形都是位似图形;
而B的对应顶点的连线不能相交于一点,故不是位似图形.
故答案为:B.
分析:如果两个多边形不仅相似,而且对应点的连线所在的直线相交于一点,对应边互相平行(或在一条直线上),像这样的两个图形叫做位似图形,据此判断即可.
6. C
考点:比例线段
解: 所以A不是成比例线段,
?所以B不是成比例线段,
?所以C是成比例线段,
?所以D不是成比例线段.
故答案为:C.
分析:先把四条线段按从小到大的顺序排列,若a,b,c,d成比例,即有a:b=c:d.只要代入验证即可.
7. D
考点:相似三角形的性质
解:相似三角形的性质:相似三角形的周长比会等于相似比.
D一定成立.
都不一定成立.
故选D.
分析:根据相似三角形的性质“①相似三角形的对应角相等.②相似三角形的对应边成比例.③相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比.④相似三角形的周长比等于相似比.⑤相似三角形的面积比等于相似比的平方.”可判断求解.
8. D
考点:相似三角形的判定
解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形对应边成比例 且夹角相等,故两三角形相似,故本选项不符合题意.
D、两三角形中,有 但夹角不一定相等,故不能判定两三角形相似,故本选项符合题意;
故答案为:D
分析:根据相似三角形的判定定理对各选项进行逐一判定即可.
9. C
考点:相似三角形的判定与性质
解:∵MN∥BC,
∴△AMN∽△ABC,
又∵点G为 △ABC的重心,
,
∴.
故答案为:C.
分析:根据相似三角形的判定可得△AMN∽△ABC,再由△ABC的重心得 , 根据相似三角形的性质:相似三角形的面积比等于相似比的平方,由此即可得出答案.
10. B
考点:相似多边形的性质
解:如图,
设AB=a, BC=b,
∵矩形ABCD∽矩形BEFA,
∴AB:BC=AF:AB,
∴a:b=b:a,
∴a2=b2,
∴b:a=:1,
故答案为:B.
分析:设短边AB=a, 长边BC=b, 由相似多边形的性质列式即可求出矩形的长边与短边的比值.
二、填空题
11. 6
考点:比例线段
解:根据比例中项的概念结合比例的基本性质,得c2=4×9,解得c=±6(线段是正数,负值舍去),
∴c=6cm,
故答案为:6.
分析:根据比例中项的定义,列出比例式即可得出c.
12. 9:4
考点:相似三角形的性质
解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,
∵BC:EF=3:2,
∴ ,
故答案为:9:4.
分析:先根据位似图形的概念得到△ABC∽△DEF,根据相似三角形的性质计算即可得到答案.
13. 3
考点:相似三角形的判定
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C
∴∠APG=∠BFP,
∴△APG∽△BFP
则图中相似三角形有3对
分析:先根据条件证明△PCF∽△BCP,利用相似三角形的性质:对应角相等,再证明△APD∽△PGD,进而证明△APG∽△BFP再证明时注意图形中隐含的相等的角.
14. ∠B=∠AED或∠C=∠ADE或
考点:相似三角形的判定
解:本题答案不唯一,
∵在△AED和△ABC中,∠A=∠A,
∴(1)当添加条件:∠B=∠AED时,△ABC∽△AED;(2)当添加条件:∠C=∠ADE时,△ABC∽△AED;(3)当添加条件: 时,△ABC∽△AED.
故答案为:∠B=∠AED?? 或∠C=∠ADE? 或 .
分析:根据相似三角形的判定定理,添加合适的条件即可。
15. 160
考点:相似多边形的性质
解:∵周长之比等于相似比,
∴这个地区的实际周长是320×50000=16000000cm=160km;
故答案为160.
分析:地图与实际的多边形按照比例放大与缩小,根据相似多边形的相似比求解即可
16.
考点:勾股定理,相似三角形的判定与性质
解:∵ ,
,
,
∴ ,
∴△ABC∽△DEF,
∴ ,
故答案为: .
分析:先证明两个三角形相似,再根据相似三角形的周长比等于相似比,得出周长比的值便可.
三、解答题
17. (1)解:设
则 , ,
∴
(2)解:∵
∴
解得
∴ , ,
考点:代数式求值,比例的性质
分析:(1)设 ,则 , , ,代入即可化简;(2)根据 得到 ,解出k即可求解.
18. 解:∵四边形ABCD是菱形,
∴BC∥AD
∴ =
∵CD∥AB
∴ =
∴ = =1
又∵AB=AD=1,
∴
=1.
答: 的值为1.
考点:菱形的性质,平行线分线段成比例
分析:根据四边形ABCD是菱形得到BC∥AD,从而得到 , , ,代入菱形的边长为1即可求得结论.
19. 证明:∵在等腰 中, 是顶角 的平分线,
∴ ⊥ ,
∴ ,
∵ 是腰 边上的高,垂足为 ,
∴ ,
∴ ,
又∵ ,
∴ ∽
考点:相似三角形的判定
分析:利用等腰三角形三线合一的性质,可证得∠ADC=90°,再利用三角形高的定义证明∠ADC=∠BEC,再利用有两组角对应相等的两三角形相似,可证得结论。
20.证明:∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=∠BAC=45°.
又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,
即四边形AFGE为正方形.
∴ = = = ,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似
考点:相似多边形的性质
分析:由正方形的性质可知;AC平分∠DAB,然后由角平分线的性质可知GE=GF,从而可证明四边形EGFA为正方形,故此四边形AFGE与四边形ABCD相似.本题主要考查的是相似多边形的判定、正方形的判定、角平分线的性质,证得四边形EAFG为正方形是解题的关键.
21. (1)解:如图,
(2)解:符合题意的三角形边长共有6个:①, 2,;②2,2, 2;③, , 5;④, 2, 5;⑤3,3, 3;⑥2, 4,2;
考点:相似三角形的判定
分析:(1)根据各点三角形的定义及相似三角形的判定方法即可得出答案;
(2)根据相似三角形的判定方法及格点三角形的定义即可得出符合题意的图形.
22. (1)解:如图所示,△A1B1C1、△A2B2C2即为所求;
(2)3
考点:作图﹣平移,作图﹣位似变换
解:(2)△AA1A2的面积为 ×6×1=3.
故答案为:3.
分析:(1)分别作出平移后对应点,再首尾顺次连接即可得;根据位似变换的概念作出变换后的对应点,再首尾顺次连接即可得;(2)利用三角形的面积公式计算可得.
23. (1)证明:∵四边形 是矩形,
∴ ,
∴ ,又 ,
∴ ,
∴ ,即 是等腰三角形;
(2)证明:作 于 ,
∵ , ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴
∴
(3)解:∵ 为 中点,
∴ ,
由(2)得, ,
∵ ,
∴ ,
∴ ,
设 ,则 ,
∵ ,
∴ ,即 ,
解得, ,即 ,
∴ ,
∴ .
考点:等腰三角形的判定,相似三角形的判定
分析:(1)由矩形的性质得出AD∥BC,由平行线的性质得出∠NAM=∠BMA,由已知∠AMN=∠AMB,得出∠AMN=∠NAM,即可得出结论;(2)由矩形的性质得出AD∥BC,AD=BC=2,AB=CD=3,由平行线的性质得出∠NAM=∠BMA,作NH⊥AM于H,由等腰三角形的性质得出AH= AM,证明△NAH∽△AMB,得出 ,即可得出结论;(3)求出BM=CM= BC= ×2=1,由(2)得AM2=2BM?AN,得出AM2=2AN,由勾股定理得出AM2=AB2+BM2=10,求出AN=5,得出DN=AN-AD=3,设DE=x,则CE=3-x,证明△DNE∽△CME,得出 ,求出DE= ,得出CE=DC-DE= ,再由勾股定理即可得出答案.
24. (1)解:由题意可知:AB=1.54-0.04=1.5m;BC=0.5m;CD=4m
∵ΔABC∽ΔEDC
∴ 即
∴
答:DE的长为12米.
(2)解:延长AD交BC的延长线于点F,过点D作DE⊥BC于点E
∵CD= m,∠DCE=45°
∴DE=CE=2m
∵
∵ 同一时刻物高与影长成正比
∴EF=2DE=4m
∴BF=EF+CE+BC=16m
∴AB= FB=8m
答:旗杆的高度约为8米.
考点:相似三角形的应用
分析:(1)根据题意得出△ABC∽△EDC,进而利用相似三角形的性质得出答案.(2)延长AD交BC的延长线于点F,过点D作DE⊥BC于点E,根据勾股定理求出ED的长,再由同一时刻物高与影长成正比得出EF的长,根据DE∥AB可知△EDF∽△ABF,由相似三角形的对应边成比例即可得出AB的长.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
