浙教版数学八年级上册课件:2.1图形的轴对称(23张ppt)
文档属性
| 名称 | 浙教版数学八年级上册课件:2.1图形的轴对称(23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 21:20:24 | ||
图片预览







文档简介
西双版纳大金塔
西双版纳
大金塔
版纳傣族园
大理崇圣寺三塔
昆明翠湖公园一角
如果用一条直线将这些图形分成两部分,它们都具有怎样特点呢?
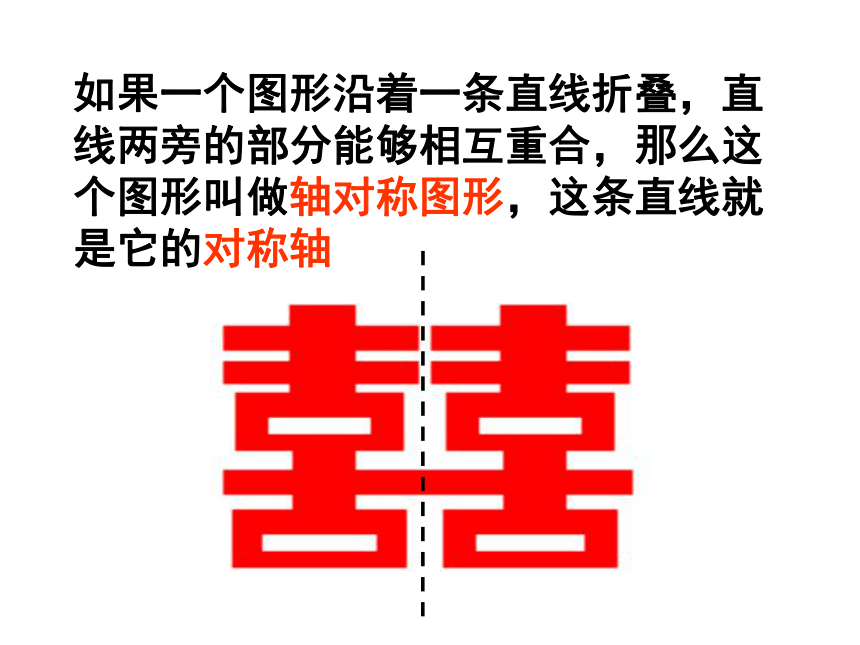
如果一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴
正方形
圆
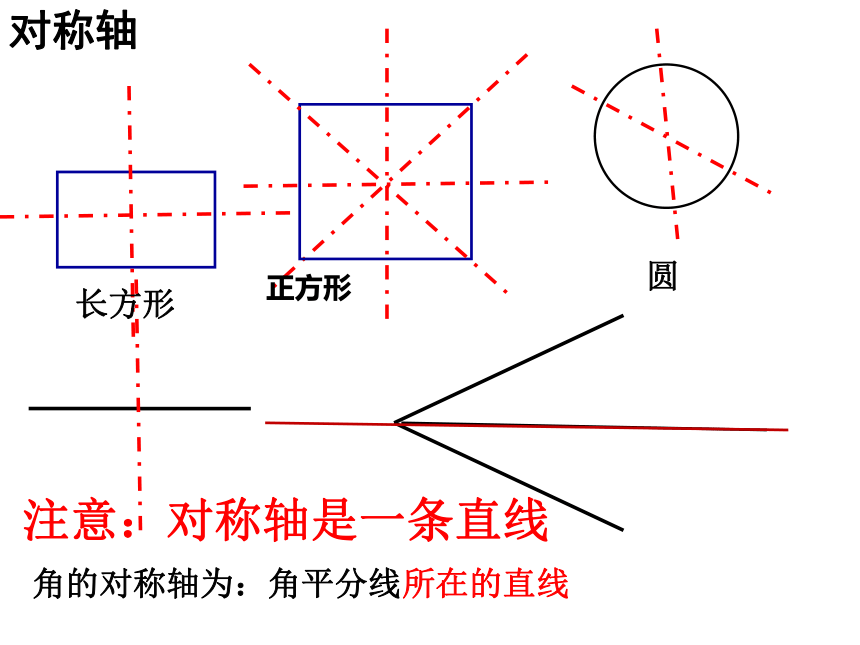
对称轴
角的对称轴为:角平分线所在的直线
注意:对称轴是一条直线
长方形
2.1 图形的轴对称
季利丹
赤溪学校
B
A
C
D
如图所示:在纸飞机折叠过程中形成的四边形ABCD是不是轴对称图形?如果是它的对称轴是什么?
哪个点与点B对称?哪个点与点A对称
点D呢?
注意:在轴对称图形中,沿对称轴折叠能重合的点叫对称点
直线AD
先完成书本48页合作学习第1题
玩转轴对称
如图所示:在四边形ABCD中,连结BC交直线AD于点E,观察并猜想BE与CE,AD与BC位置的关系,并说明理由.
结论:AD垂直平分BC
BE=CE,AE⊥BC
玩转轴对称
推断AD与BC的关系
你还能再找到这样的对称点吗?
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段.
轴对称图形中,连结任意两个对称点的线段与对称轴都有什么关系?
玩转轴对称
人机合一
.
A
已知点A和直线l,你能作出它关于l的对称点A’吗?
作图依据是什么?
l
玩转轴对称
轴对称图形的性质
B
C
.A’
O
例1 如图,已知△ABC和直线m,以直线m为对称轴求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’.
2.依次连结A’B’,B’C’,C’A’.
∴ △ A’B’C’就是所求作的三角形.
玩转轴对称
1.分别作点A,B,C的对称点A’,B’, C’
玩转轴对称
生活中如何快速得到一个
与你长得一模一样的你?
人图合一
图形的轴对称:
两个图形成轴对称
一般地,由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样图形的改变叫图形的轴对称,这条直线叫做对称轴
如果把图1沿直线m折叠,那么 △ A’B’C’就和△ ABC重合,这时我们说△ A’B’C’和△ ABC成轴对称。
图1
玩转轴对称
1.成轴对称的两个图形的大 小和形状有什么关系?
2. 轴对称图形和图形的轴对称有什么联系和区别?
思考:
图形的轴对称的性质:成轴对称的两个图形是全等图形
如果把一个轴对称图形沿对称轴分成两个图形,这两个图形 ,并也是 .
全等
成轴对称
成轴对称的两个图形 ,并且像与原像组合成 .
全等
一个轴对称图形
2.如图,已知直角三角形ABC
(1)以直角边AC所在 的直线为对称轴,作出与直角三角形ABC成轴对称的图形
(2)第(1) 作出的图形和原图组成一个等腰三角形吗?请说明理由.
玩转轴对称
∵△ABC与△AB’C成轴对称
∴ △ABC≌△AB’C(图形的轴对称性质)∴∠ACB=∠ACB’=90°
∴∠BCB’=180°即B,C,B’三点共线
又∵AB=AB’(全等三角形对应边相等)∴△ABB’是等腰三角形
生活应用
①如图1,直线 是一条溪流,在这条溪流 旁有两个村庄A、B,骑马少年从A村出发去溪流中饮水后到B村去,他沿怎样的路线行走,能使路最短?作出这条最短路线;
A
.
.
B
玩转轴对称
两
生活应用
①如图1,直线 是一条溪流,在这条溪流 旁有两个村庄A、B,骑马少年从A村出发去溪流中饮水后到B村去,他沿怎样的路线行走,能使路最短?作出这条最短路线;
A
.
玩转轴对称
同
.
B
(1)设点P是直线l上的一点,则骑马少年所行的路程可以表示为 ,
(2)画出A关于直线l的对称点A’, 则骑马少年所行的路程可以表示为 .
A
B
A’
C
作法:
(1)作点A关于直线 l 的对称点 A’;
(2)连结A’B,交l于点C;
∴沿折线A-C-B行走能使路线最短.
玩转轴对称
作点A的对称点改作点B的对称点能不能找到这样的点C,画出来试试。为什么?
同化异,折转直,
轴对称,最值美。
归纳:已知一条直线同侧的两个点,如何在直线上找一点使到两点的距离之和最小?
玩转轴对称
实验中学知识树模板
轴对称图形
联系和区别
一个图形对称轴
两侧成轴对称
对称轴两侧
图形全等
轴对称图形
的性质
图形的轴对称
对称轴
两个图形
成轴对称
图形的轴对称
的性质
组合
最值
分离
轴对称
应用
玩转轴对称
谢谢
请批评指正
西双版纳
大金塔
版纳傣族园
大理崇圣寺三塔
昆明翠湖公园一角
如果用一条直线将这些图形分成两部分,它们都具有怎样特点呢?
如果一个图形沿着一条直线折叠,直线两旁的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴
正方形
圆
对称轴
角的对称轴为:角平分线所在的直线
注意:对称轴是一条直线
长方形
2.1 图形的轴对称
季利丹
赤溪学校
B
A
C
D
如图所示:在纸飞机折叠过程中形成的四边形ABCD是不是轴对称图形?如果是它的对称轴是什么?
哪个点与点B对称?哪个点与点A对称
点D呢?
注意:在轴对称图形中,沿对称轴折叠能重合的点叫对称点
直线AD
先完成书本48页合作学习第1题
玩转轴对称
如图所示:在四边形ABCD中,连结BC交直线AD于点E,观察并猜想BE与CE,AD与BC位置的关系,并说明理由.
结论:AD垂直平分BC
BE=CE,AE⊥BC
玩转轴对称
推断AD与BC的关系
你还能再找到这样的对称点吗?
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段.
轴对称图形中,连结任意两个对称点的线段与对称轴都有什么关系?
玩转轴对称
人机合一
.
A
已知点A和直线l,你能作出它关于l的对称点A’吗?
作图依据是什么?
l
玩转轴对称
轴对称图形的性质
B
C
.A’
O
例1 如图,已知△ABC和直线m,以直线m为对称轴求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’.
2.依次连结A’B’,B’C’,C’A’.
∴ △ A’B’C’就是所求作的三角形.
玩转轴对称
1.分别作点A,B,C的对称点A’,B’, C’
玩转轴对称
生活中如何快速得到一个
与你长得一模一样的你?
人图合一
图形的轴对称:
两个图形成轴对称
一般地,由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样图形的改变叫图形的轴对称,这条直线叫做对称轴
如果把图1沿直线m折叠,那么 △ A’B’C’就和△ ABC重合,这时我们说△ A’B’C’和△ ABC成轴对称。
图1
玩转轴对称
1.成轴对称的两个图形的大 小和形状有什么关系?
2. 轴对称图形和图形的轴对称有什么联系和区别?
思考:
图形的轴对称的性质:成轴对称的两个图形是全等图形
如果把一个轴对称图形沿对称轴分成两个图形,这两个图形 ,并也是 .
全等
成轴对称
成轴对称的两个图形 ,并且像与原像组合成 .
全等
一个轴对称图形
2.如图,已知直角三角形ABC
(1)以直角边AC所在 的直线为对称轴,作出与直角三角形ABC成轴对称的图形
(2)第(1) 作出的图形和原图组成一个等腰三角形吗?请说明理由.
玩转轴对称
∵△ABC与△AB’C成轴对称
∴ △ABC≌△AB’C(图形的轴对称性质)∴∠ACB=∠ACB’=90°
∴∠BCB’=180°即B,C,B’三点共线
又∵AB=AB’(全等三角形对应边相等)∴△ABB’是等腰三角形
生活应用
①如图1,直线 是一条溪流,在这条溪流 旁有两个村庄A、B,骑马少年从A村出发去溪流中饮水后到B村去,他沿怎样的路线行走,能使路最短?作出这条最短路线;
A
.
.
B
玩转轴对称
两
生活应用
①如图1,直线 是一条溪流,在这条溪流 旁有两个村庄A、B,骑马少年从A村出发去溪流中饮水后到B村去,他沿怎样的路线行走,能使路最短?作出这条最短路线;
A
.
玩转轴对称
同
.
B
(1)设点P是直线l上的一点,则骑马少年所行的路程可以表示为 ,
(2)画出A关于直线l的对称点A’, 则骑马少年所行的路程可以表示为 .
A
B
A’
C
作法:
(1)作点A关于直线 l 的对称点 A’;
(2)连结A’B,交l于点C;
∴沿折线A-C-B行走能使路线最短.
玩转轴对称
作点A的对称点改作点B的对称点能不能找到这样的点C,画出来试试。为什么?
同化异,折转直,
轴对称,最值美。
归纳:已知一条直线同侧的两个点,如何在直线上找一点使到两点的距离之和最小?
玩转轴对称
实验中学知识树模板
轴对称图形
联系和区别
一个图形对称轴
两侧成轴对称
对称轴两侧
图形全等
轴对称图形
的性质
图形的轴对称
对称轴
两个图形
成轴对称
图形的轴对称
的性质
组合
最值
分离
轴对称
应用
玩转轴对称
谢谢
请批评指正
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
