7.6余角和补角

(共18张PPT)
1
2
α
β
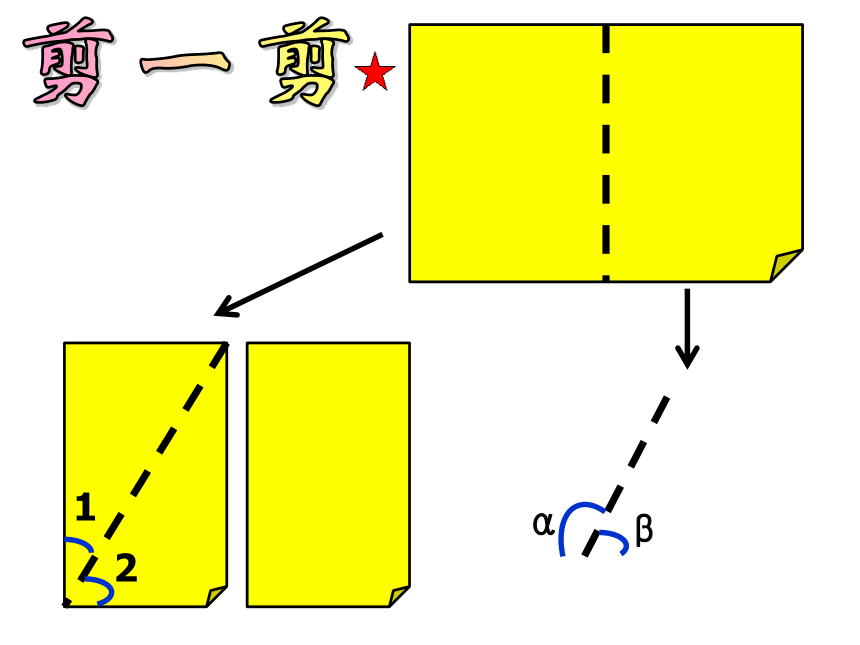
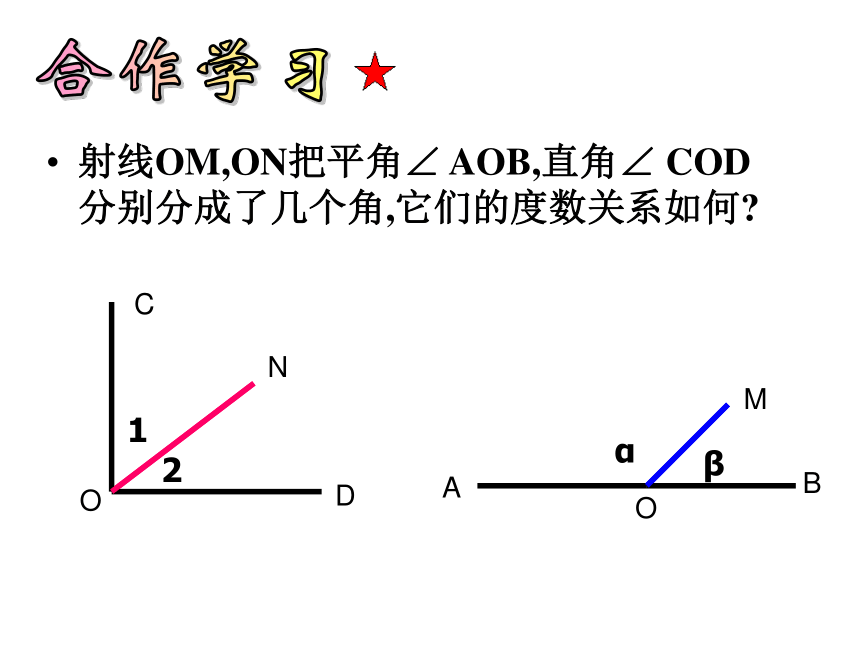
射线OM,ON把平角∠ AOB,直角∠ COD分别分成了几个角,它们的度数关系如何
1
β
α
M
O
B
A
O
2
D
C
N
1
2
3
4
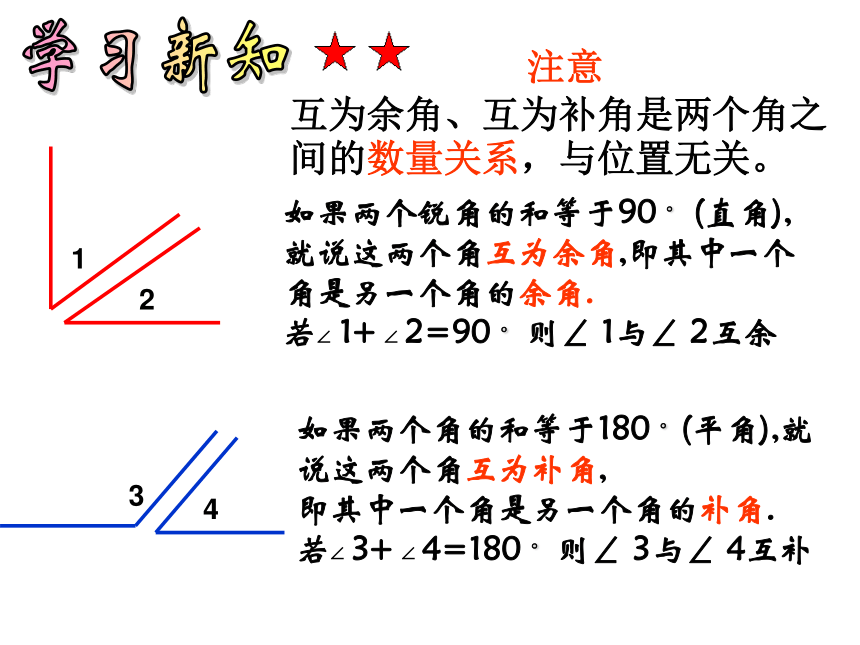
如果两个锐角的和等于90 ° (直角),
就说这两个角互为余角,即其中一个
角是另一个角的余角.
若∠ 1+ ∠ 2=90 ° 则∠ 1与∠ 2互余
如果两个角的和等于180 °(平角),就说这两个角互为补角,
即其中一个角是另一个角的补角.
若∠ 3+ ∠ 4=180 ° 则∠ 3与∠ 4互补
注意
互为余角、互为补角是两个角之间的数量关系，与位置无关。
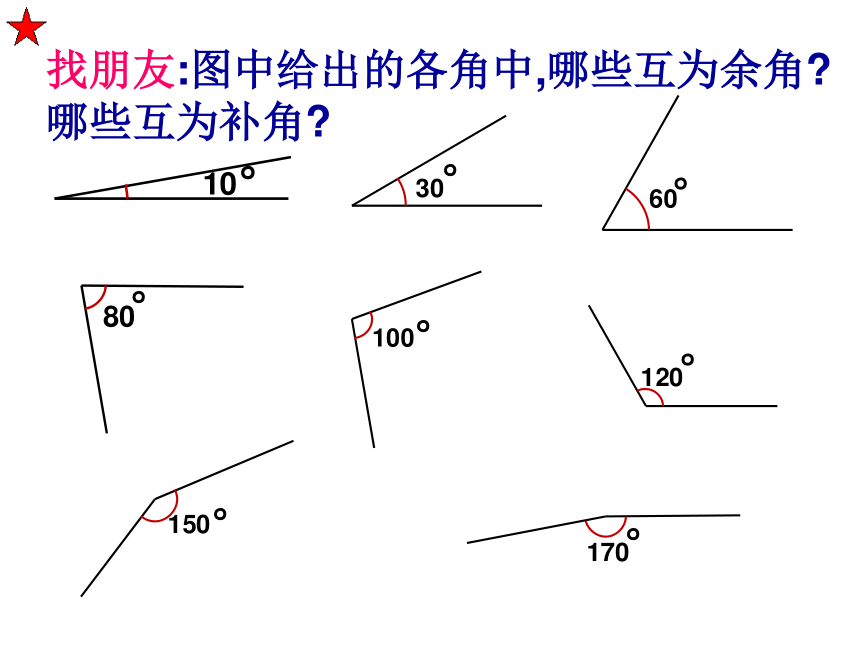
找朋友:图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
1、到底谁是真的：
　 互余的两个角必定都是锐角。 　
一个角的补角必定是钝角。
　
两个角互补，那么这两个角中，
必定一个是锐角，另一个是钝角。 　


练习：

1、定义中的“互为”一词如何理解？
2、互补、互余的两角是否一定有公共顶点或公共边？
3、 1与 2互补，除用符号语言表示为 1＋ 2＝180°外，还可以用其它形式等式表示为______。
如果 1与 2互补，那么 1的补角是 2 ，而 2的补角是 1 ；如果 1与 2互余，那么 1的余角是 2 ， 2的余角是 1。
互补或互余的两角度数之间的数量关系，与两角位置无关！
1＝180°－ 2，或 2＝180°－ 1
思考：60°的余角的补角是______。
∠α ∠α的余角 ∠α的补角
5° 85° 175°
32° 58° 148°
45° 45° 135°
77° 13° 103°
62°23′ 27°37′ 117°37′
x 90°-x 180°-x
90°-β β β+90°
30度角
150°
∠2=∠3，∠2和∠α互余，∠3和∠β互余
C
D
2
3
1
O
A
B
3
2
β
α
同角 的余角相等 。
或等角
1
∠2=∠3，∠2和∠α互补，∠3和∠β互补
C
D
2
3
O
A
B
α
β
同角 的补角相等 。
或等角
2
3
如图，直线CD经过点O，且OC平分∠AOB。试判断∠AOD与∠BOD的大小关系，并说明理由。
O
D
A
B
C
答：∠AOD=∠BOD
因为∠AOD与∠AOC互补，∠BOD与∠BOC互补
所以∠AOD=180°- ∠AOC
∠BOD=180°-∠BOC
又因为OC平分∠AOB
所以∠AOD=∠BOD
（等角的补角相等）
所以∠AOC=∠BOC
已知一个角的补角是这个角的余角的4倍，求这个角的度数。
利用方程来解决几何问题
　　互余的角 　　互补的角
数量关系 　
　 　
　　
对应图形
性质
C
D
E
N
A
O
B
M
1＋ 2＝90°
1＋ 2＝180°
同角(等角)的余角相等
同角(等角)的补角相等
1
海塘大坝要修复加固，施工前要求先测出大坝的倾斜角（即图中的∠1），坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法？
想一想
看谁思考的快！！
　　1．锐角的余角一定是锐角吗？
　　2．一个锐角和一个钝角一定互为补角吗？
　　3．一个角的补角比这个角的余角大多少度？
　　4．相等且互补的两个角各是多少度？
　　5．一个角的补角一定比这个角大吗？
一定
（不一定）
（大90°）
（90°、 90°）
（不一定）
1.如果∠1＋∠3＝90°
那么∠1与∠3互为余角
2.如果∠1与∠3互为余角
那么∠1＋∠3＝90°
3
1
1
3
1
3
3
1
1
2
那么∠1＋∠2＝180°
4.如果∠1与∠2互为补角
那么∠1与∠2互为补角
3.如果∠1＋∠2＝180°
2
1
1
2