2.5直角三角形[1]

(共25张PPT)
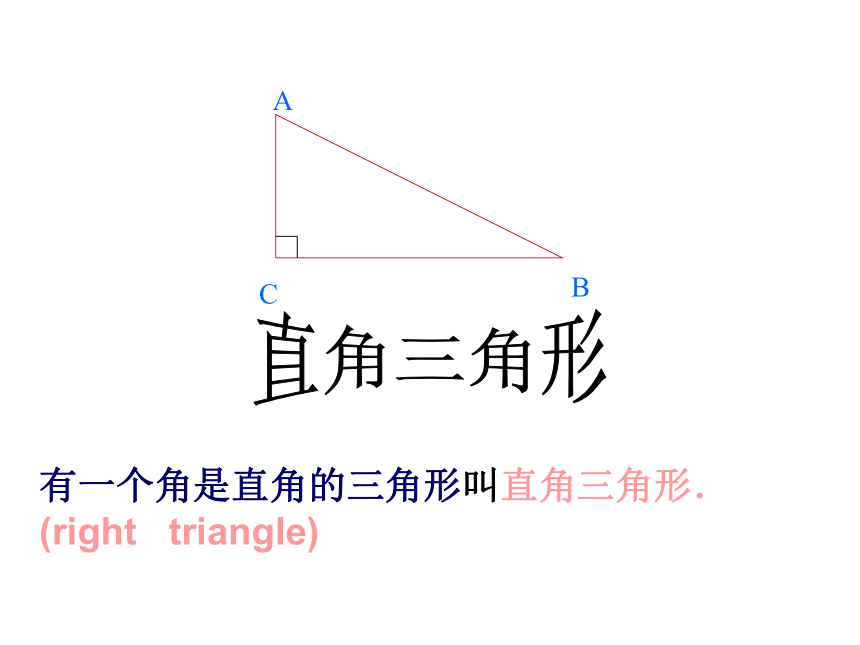
有一个角是直角的三角形叫直角三角形．
(right triangle)
A
C
B
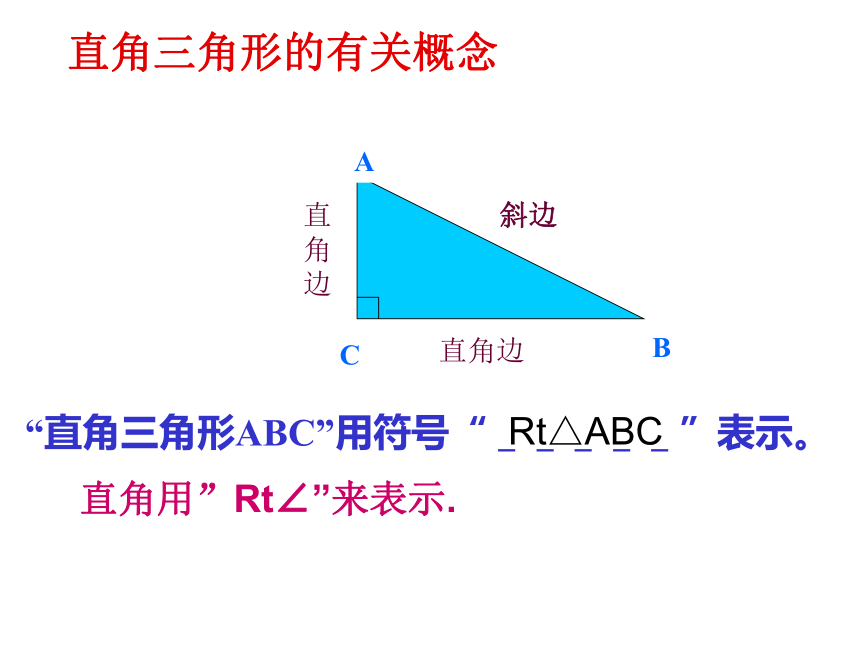
直角边
直角边
斜边
“直角三角形ABC”用符号“＿＿＿＿＿”表示。
A
C
B
Rt△ABC
直角用”Rt∠”来表示.
直角三角形的有关概念
你能找出你身边的哪些物体有直角三角形的形状吗
想一想：
你能举出生活中一些含有直角三角形的例子吗？
（1）直角三角形的内角有什么特点？
（2）怎样判定一个三角形是直角三角形？
1. 一个内角为90。
2.另两个内角互余
1.说明一个角为直角
2.说明有两个角互余
请讨论下面的问题：
合作学习

C
A
B
A
B
C
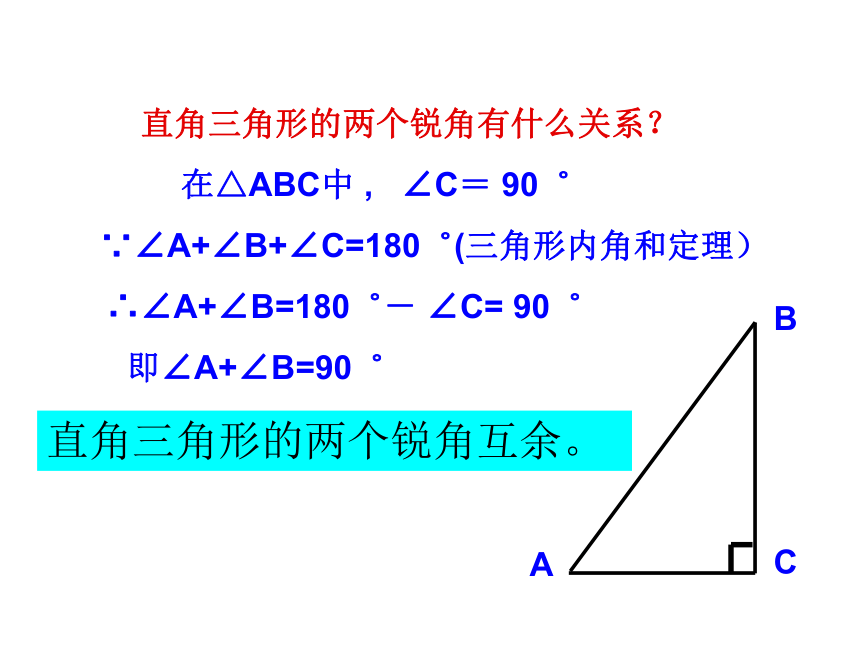
直角三角形的两个锐角有什么关系？
直角三角形的两个锐角互余。
在△ABC中 , ∠C＝ 90゜
∵∠A+∠B+∠C=180゜(三角形内角和定理）
∴∠A+∠B=180゜－ ∠C= 90゜
即∠A+∠B=90゜
反过来：有两个角互余的三角形是直角三角形．成立吗？
A
C
B
有两个角互余的三角形是直角三角形.
在△ABC中 , ∠A＋∠B＝90 ゜
∵∠A+∠B+∠C=180゜(三角形内角和定理）
∴ ∠C＝ 180 ゜ －( ∠A+∠B)=180 ゜ － 90゜ = 90゜
∴ △ABC是直角三角形．
直角三角形的两个锐角互余。反过来，有两个角互余的三角形是直角三角形。
（1）直角三角形的内角有什么特点？
（2）怎样判定一个三角形是直角三角形？
1. 一个内角为90。
2.另两个内角互余
1.说明一个角为直角
2.说明有两个角互余
请讨论下面的问题：
C
A
B
合作学习

结论

两条直角边相等的直角三角形叫做等腰直角三角形.
等腰直角三角形的两个底角相等，等于４５ ゜.
请观察图1中的△ABC,这个三角形有什么特点
B
C
A
AB=AC
思考：等腰直角三角形的两个底角各是多少度呢？
图1
∠A=90°
１．直角三角形的两个锐角互余．
２．有两个角互余的三角形是直角三角形．
３．等腰直角三角形的两个锐角都是４５ ゜
小结

１．如图，ＣＤ是Ｒｔ△ABC斜边上的高．请找出图中各对互余的角.
Ｃ
Ｄ
Ａ
Ｂ
解：∵ＣＤ⊥ＡＢ，
∴ △ＡＣＤ， △ＢＣＤ都是Ｒｔ△，
又已知△ABC是Ｒｔ△，
∴ ∠Ａ与∠Ｂ． ∠Ａ与∠ACＤ．
∠Ｂ与∠ＢＣＤ互余．
又∵ ∠ＡＣＢ＝Ｒｔ∠
∴ ∠ＡＣＤ与∠ＢＣＤ互余．
所以图中共有４对互余的角．　
∟
∟
想一想:图中除了直角外,还有相等的角吗
∠ACD=∠B，
∠BCD=∠A。
解：∵ ∠1=∠B，∠2=∠A，
　　∴∠1+ ∠2+ ∠A+ ∠B
=2(∠A+ ∠B) =180°
∴ ∠A+ ∠B= 90°
∴ △ABC是Rt△(有两个角互余的三角形是直角三角形)
如图，在△ABC中，D是AB上一点，若∠1=∠B， ∠2=∠A，则△ABC是Rt△，请说明理由。
B
1
2
A
D
C
D
在一次劳技课中，老师布置了一个小任务，要求同学们将一个大的等腰直角三角形一刀剪成两个小的等腰直角三角形，小明发愁了不知该怎么剪好，聪明的你能利用手头上的等腰直角三角形帮帮他吗？
A
B
C
等腰直角三角形斜边上的高把等腰直角三角形划分为两个等腰直角三角形.
你能在一张长方形的纸片上折出一个等腰直角三角形吗？
请动手折一折，并请说明折法和理由。
请画出示意图并说明理由
动一动

想一想

2．如图：在等腰直角三角形ABC中，AD是斜边BC上的高，则AD＝BD＝CD．请说明理由．
Ａ
Ｂ
Ｃ
Ｄ
解：∵ △ABC是个等腰直角三角形
　　∴∠B=∠C=45°
　　∵AD⊥BC（已知）
　　∴∠CAD+ ∠C=90 °
∴∠CAD=90°—∠C
=90°— 45°
=45°= ∠C
∴AD=DC（？）
　　同理可得，AD=BD
∴AD=BD=CD
1、直角三角形ABC中,AD是斜边BC上的高,
　　则图中共有等腰直角三角形____个.
２、如果三角形一边上的高平分这边所对的角,那么此三角形一定是 ( 　 )
(A)等腰三角形. (B) 直角三角形.
(C) 等边三角形. (D) 等腰直角三角形.
A
B
D
C
3
A
练一练

如图，已知△ABC中，点A在DE上，CD⊥DE，BE⊥DE，垂足分别是D，E．且AD＝BE，CD＝AE， △ABC是等腰直角三角形吗？说明理由．
Ｅ
Ｄ
Ａ
Ｃ
Ｂ
☆★☆★
☆★☆★
1. 在Ｒｔ△ABC中∠Ｃ＝９０ ゜ ,∠Ａ＝５４ ゜
则∠Ｂ＝___.
2.在Rt △ABC中， ∠C= 90。， ∠ A - ∠ B=20 。 ，
则∠ A=______度, ∠ B=_____度
2. 在Rt △ABC中，∠C= 90。 ， CD ⊥ AB，
∠ A ：∠ B=1 ：2，则∠ACD= _____，
∠BCD= _____
30 。
55 。
35 。
60 。
C
A
B
D
36 。
练一练

１．在Ｒｔ△ABC中∠Ｃ＝９０ ゜ ,∠Ａ＝５8 ゜ ．
则∠Ｂ＝___.
2.如图:在等腰直角三角形ABC中,AD是斜边BC上的高,则图中共有等腰直角三角形____个.
3.如图,在△ABC中, ∠ ACB=90, AE平分∠ CAB,
CD ⊥ AB于D, 它们交于点F, △ CFE是等腰三角形吗 试说明理由.
A
B
D
C
A
D
F
C
E
B
32 ゜
3
∟
∟
4．如图：AF是Rt△ABC斜边BC边上的高， 　　 AD是∠BAC的平分线，且∠B＝35°，求∠FAC和∠DAF的度数。
Ａ
Ｂ
Ｄ
Ｆ
Ｃ
∠FAC=35°
∠DAF=10°
5.将一张长方形纸片按图示方法折叠，得到 △ABC是等腰直角三角形.请说明理由.
A
C
B
6.如图的七巧板结构图中如果大正方形的边长为4cm，请求出最小一块直角三角形的面积。
1. 直角三角形的概念
2．直角三角形的两个锐角互余．
3．有两个角互余的三角形是直角三角形．
4．等腰直角三角形的两个锐角都是45° ．