二次函数的复习[1]

(共18张PPT)
二次函数单元复习
知识回顾
概念：
定义域：
图像：
形如y=ax2+bx+c(a≠0)的函数是二次函数
一切实数
抛物线
基础训练
已知函数 ， 当m= 时，它是二次函数
0
知识回顾
二次函数的图像性质：
y=ax2+bx+c
（-m,k）
开口向上
x=-m
y=a(x+m)2+k
函数 开口方向 对称轴 顶点坐标
a>0 a<0
开口向上
开口向下
开口向下
基础训练
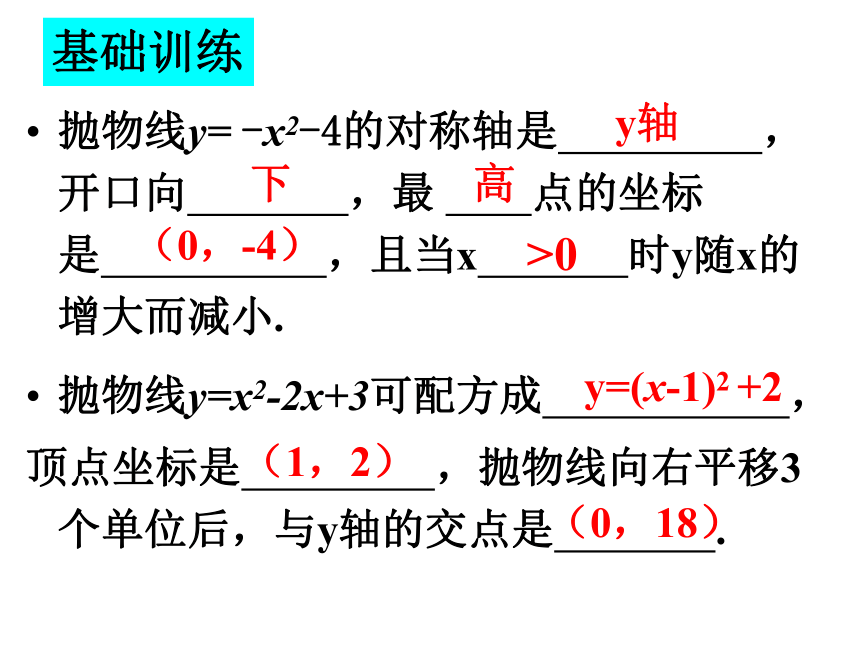
抛物线y= -x2-4的对称轴是 ，开口向 ，最 点的坐标是 ，且当x 时y随x的增大而减小.
抛物线y=x2-2x+3可配方成 ，
顶点坐标是 ，抛物线向右平移3个单位后，与y轴的交点是 .
（0，-4）
y轴
下
高
>0
y=(x-1)2 +2
（1，2）
（0，18）
知识回顾
二次函数y=ax2+bx+c(a≠0)的系数a、b、c对图像的影响：
（1）a的符号决定抛物线的开口方向，
决定开口大小
（2）a、b同号时抛物线的对称轴在y轴的左侧
a、b异号时抛物线的对称轴在y轴的右侧
（3）抛物线与y轴的交点坐标是（0，c）
c决定抛物线与y轴的交点位置
（4）b2-4ac>0，抛物线与x轴有两个公共点
b2-4ac=0，抛物线与x轴有一个公共点
b2-4ac<0，抛物线与x轴没有公共点
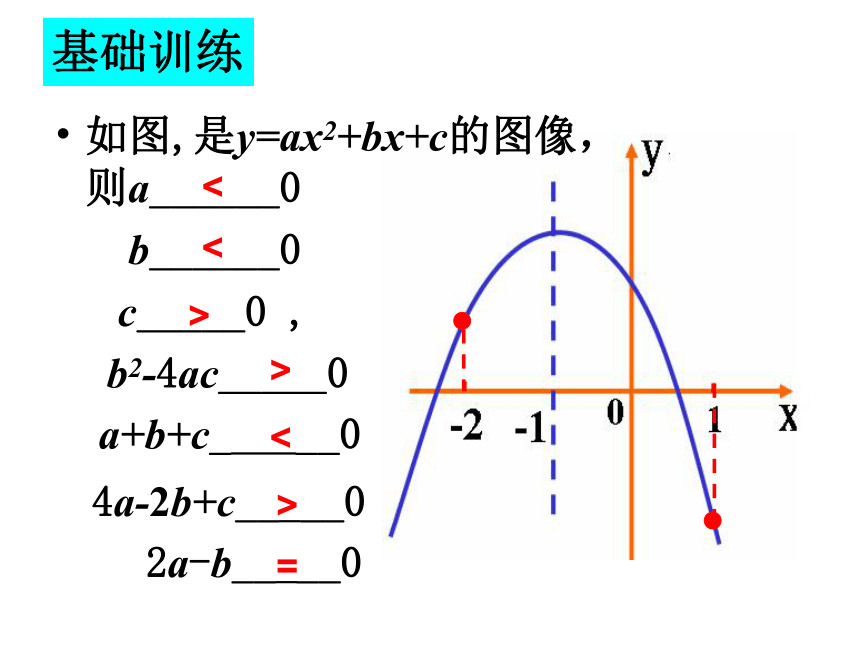
如图,是y=ax2+bx+c的图像，则a______0
b______0
c_____0 ,
b2-4ac_____0
基础训练
<
<
>
>
a+b+c_ __0
4a-2b+c__ __0
>
<
2a-b__ __0
=
图像性质题
（填空、选择）
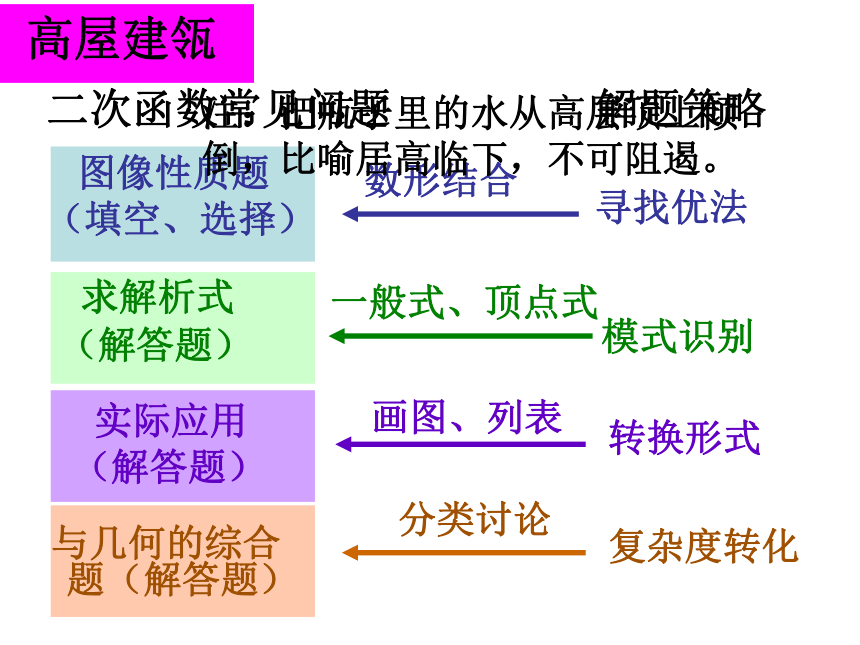
高屋建瓴
二次函数常见问题
实际应用
（解答题）
与几何的综合题（解答题）
解题策略
寻找优法
模式识别
转换形式
复杂度转化
数形结合
画图、列表
一般式、顶点式
分类讨论
求解析式
（解答题）
注：把瓶子里的水从高层顶上倾倒，比喻居高临下，不可阻遏。
1、抛物线y=ax2+bx+c中，若a<0,b>0,
c>0，则它的顶点在第 象限
——图像性质题
高屋建瓴
一
x
y
0
y2
2、抛物线y1=x2+bx+c与直线y2=mx+n交于A、B两点，且A(-2,-3)，B(2,5)，若y1——图像性质题
x
y
0
A
B
-2y1
高屋建瓴
——求解析式
3、已知二次函数y=f(x)中，f(0)=f(-1)=-1,且它的图像的最高点的纵坐标是 ，
求这个函数的解析式.
模式识别：顶点式
顶点（ ， ）+点（0，-1）
高屋建瓴
——求解析式
4、已知二次函数y=ax2+bx+c中，x与y的部分对应值如下表，求这个函数的解析式.
模式识别：一般式
x -2 -1 0 1 2 3
y -16 -6 0 2 0 -6
可选三点（0，0）+（-1，6）+（1，2）
高屋建瓴
——求解析式
5、已知一条抛物线的对称轴是直线x=1，它与x轴相交于A、B两点(点A在点B的左边)且线段AB的长是4，它还与过点C(1，-2)的直线有一个交点是点D(2,-3)，求抛物线的解析式
模式识别：
顶点式
若这条抛物线有P点，使S△ABP=12，求点P的坐标
高屋建瓴
——实际应用
6、某食品零售店为食品厂代销一种面包，统计销售情况发现，当这种面包的单价定为7角时，每天卖出160个，在此基础上，这种面包的单价每提高1角时，该零售店每天就会少卖出20个。该零售店每个面包的成本是5角。设这种面包的单价为x（角），零售店每天销售这种面包所获得的利润为y（角）.
求y与x之间的函数关系式.
单价(角) 日销售量(个) 日利润(角)
提价前
提价后
7
160
160-20(x-7)
(7-5) ×160
x
(x-5)[160-20(x-7)]
y=(x-5)[160-20(x-7)]=……
高屋建瓴
——实际应用
7、某工厂现有80台机器，每台机器平均每天生产384件产品。现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品。如果设增加x台机器，每天的生产总量为y件，请你写出y与x之间的关系式.
增加前
增加后
80
384
384-4x
80×384
80+x
(80+x)(384-4x)
y=(80+x)(384-4x)=……
机器数量(台)
生产效率(件/台)
日生产总量(件)
高屋建瓴
——实际应用
8、如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x +0.9x+10表示,而且左右两条抛物线关于y轴对称．
⑴钢缆的最低点到桥面的距离是_____;
⑵两条钢缆最低点之间的距离是_____;
(3)右边的抛物线解析式是_________________.
y/m
x/m
桥面 -5 0 5
10
高屋建瓴
——实际应用
8、
⑴钢缆的最低点到桥面的距离是_____;
⑵两条钢缆最低点之间的距离是_____;
(3)右边的抛物线解析式是_________________.
y/m
x/m
桥面 -5 0 5
10
1米
40米
抛物线顶点的纵坐标是
两条抛物线顶点间的距离是
关于y轴对称的抛物线是
高屋建瓴
——函数与几何的综合题
9、如图，抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．
（1）求A、B、C三点的坐标．
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
（3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴
于点G，使以A、M、G三点为顶点的三角形与△PCA相似．
若存在，请求出M点的坐标；否则，请说明理由．
C
P
B
y
A
x
O
高屋建瓴
仔细审题，积极思考